Volume 2012, Issue 1 467412

Research Article

Open Access

Spatial Images Feature Extraction Based on Bayesian Nonlocal Means Filter and Improved Contourlet Transform

Pengcheng Han

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Junping Du,

Corresponding Author

Junping Du

[email protected]

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Pengcheng Han,

Pengcheng Han

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Junping Du,

Corresponding Author

Junping Du

[email protected]

Beijing Key Laboratory of Intelligent Telecommunication Software and Multimedia, School of Computer Science, Beijing University of Posts and Telecommunications, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

First published: 04 June 2012

https://doi.org/10.1155/2012/467412

Citations: 3

Academic Editor: Baocang Ding

Share a link

Email
Wechat
Bluesky

Abstract

Spatial images are inevitably mixed with different levels of noise and distortion. The contourlet transform can provide multidimensional sparse representations of images in a discrete domain. Because of its filter structure, the contourlet transform is not translation-invariant. In this paper, we use a nonsubsampled pyramid structure and a nonsubsampled directional filter to achieve multidimensional and translation-invariant image decomposition for spatial images. A nonsubsampled contourlet transform is used as the basis for an improved Bayesian nonlocal means (NLM) filter for different frequencies. The Bayesian model adds a sigma range in image a priori operations, which can be more effective in protecting image details. The NLM filter retains the image edge content and assigns greater weight to similarities for edge pixels. Experimental results both on standard images and spatial images confirm that the proposed algorithm yields significantly better performance than nonsubsampled wavelet transform, contourlet, and curvelet approaches.

1. Introduction

In spatial rendezvous and docking, spatial images are obtained by multisource remote sensors. Spatial images are inevitably mixed with different levels of noise and distortion. The accurate image feature extraction will be helpful for spatial object recognition and can directly influence the success of spatial rendezvous and docking [1, 2]. Image feature extraction of spatial images is based on the definition of image features; to some extent, it can be said that it is based on sensitivity changes to image grayscale values for the human eye. Multidimensional image representation can process images for the sparsest representation, especially for 2D image signals [3, 4]. This approach identifies optimal high-dimensional function representation for an image and yields superior image-processing results for an effective solution. A nonlocal means (NLM) filter uses redundant image information on the basis that structural similarity superimposed on pixel noise is random and noise can be effectively removed using weighted averages [5, 6]. Compared to traditional statistical filtering methods, NLM filtering overcomes the constraint of the local neighborhood and extends pixel similarity to block-based similarity, so it is very suitable to deal with spatial images.

In this paper, we use a nonsubsampled pyramid structure and a nonsubsampled directional filter to achieve multidimensional and translation-invariant image decomposition for spatial images. A nonsubsampled contourlet transform is used as the basis for an improved Bayesian nonlocal means (NLM) filter for different frequencies. The Bayesian model adds a sigma range in image a priori operations, which can be more effective in protecting image details. The NLM filter retains the image edge content and assigns greater weight to similarities for edge pixels. Experimental results both on standard images and spatial images confirm that the proposed algorithm yields significantly better performance than nonsubsampled wavelet transform, contourlet, and curvelet approaches.

The rest of this paper is organized as follows. Section 2 describes multidimensional image decomposition, with a focus on contourlet and nonsubsampled contourlet transforms (NSCTs). Section 3 outlines application of an NLM filter and proposes an improved NLM algorithm based on a Bayesian model. Section 4 applies the improved NLM filter to NSCT, especially NSDFB, to process image features for further extraction. Section 5 compares feature extraction results for the proposed algorithm and other algorithms. Section 6 concludes the paper.

2. Contourlet Transform Decomposition

2.1. Multidimensional Image Decomposition

The target of image multidimensional representation is to provide a description of image with less characteristic information. The wavelet transform is a classic image multidimensional representation algorithm that has a good effect on image edge points [7, 8]. However, the wavelet transform can capture only limited direction information in the horizontal, vertical, and diagonal directions, as shown in the left side of Figure 1. It is difficult to express image smoothness contours; a better image representation is shown in the right side of Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Multidimensional image decomposition.

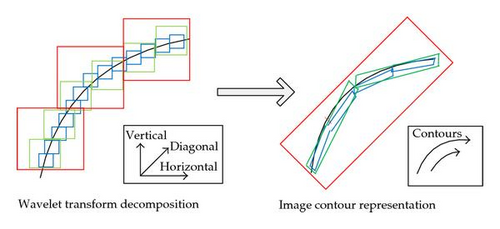
Other well-known multidimensional image decomposition algorithms include bandlets, brushlets, edge multidimensional transform, complex wavelets, and wedgelet. However, these algorithms require image edge detection and then summarize a representative adaptive coefficient. A decomposition algorithm that can transform an image into fixed decomposition coefficients is desirable. These coefficients can then be used in a broader context that does rely on edge detection alone but also includes better directional image decomposition.

In 2004, Candès and Donoho proposed a curvelet transform that uses a value approximation algorithm for a continuous 2D spatial domain and adds a smooth signal on the basis of a 1D Fourier transform [9]. The best approximation deviation is O((log M)³M⁻²) for curvelet and O(M⁻¹) for wavelet transforms. The curvelet transform is first applied to a continuous signal and then combines a multidimensional filter and ridgelet transformation. A second curvelet transform is based on frequency segments and extreme judgment. The curvelet transform is universally applicable to continuous signals, but there will be parallel noise in discrete fields [10]. It is also biased in directional image decomposition. The reason is that the typical rectangular sampling mode leads to a priori geometric deviation in decomposition of discrete image signals, especially in the horizontal and vertical directions. This limitation prompted researchers to develop a new multiscale decomposition algorithm that does not depend on edge detection and can decompose images in cross-scale multidimensions.

2.2. Contourlet Transform

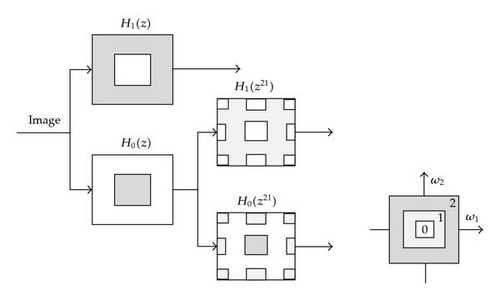
The contourlet transform is a multidimensional decomposition algorithm proposed by Do and Vetterli in 2005 [11]. The transform can be directly used for multidimensional decomposition of discrete image signals. It has a dual filter for image decomposition and yields a smoother sparse representation of the original image. The two filters are a Laplacian pyramid (LP) filter [12, 13] and a directional filter bank (DFB) [14]. The LP yields nonconsecutive image points, and then the DFB connects consecutive points into a nonlinear structure. The process is shown in Figure 2.

A subsample contourlet transform uses a relevance factor M for image subsampling at each decomposition level. A 2D filter is evolved from the 1D filter. For complete image reconstruction, the following relationship holds for the 1D filter:

(2.1)

where M₀(z) and M₁(z) represent low- and high-pass analysis filters, and N₀(z) and N₁(z) represent low- and high-pass synthesis filters, respectively. Downsampling matrices S_m are shown above. For 2D complete decomposition,

(2.2)

M^′(z) represents discrete properties of the heterogeneous domain, which can help to reduce the filter complexity from O(N²) to O(N). In two dimensions, the first DFB step is construction of the spectrum in the frequency domain using two-channel quincunx filter banks to decompose an image into horizontal and vertical directions [15]. The DFB equivalent parallel family is

(2.3)

Cutting operations on both directions for the decomposition spectrum provide 2D directional and segmental image decomposition. Like the discrete wavelet transform, the discrete downsampling contourlet transform is shift-invariant [16].

2.3. Nonsubsampled Contourlet Transform

NSCT is a fast implementation of the contourlet transform that provides a shift-invariant and multidimensional image representation [17]. Compared with subsampled contourlet transforms, NSCT is closer to the nonredundant wavelet transform [18]. NSCT uses a 2D nonsubsampled filter bank and can be expressed as

(2.4)

where M(z) represents a 2D filter of the z transform, M₀(z) and M₁(z) represent 2D low- and high-pass analysis filters, and N₀(z) and N₁(z) represent 2D low- and high-pass synthesis filters, respectively. There are also other limitations for the filter design.

NSCT involves two steps: multidimensional representation and directional decomposition. Multidimensional representation is achieved by nonsubsampled pyramid decomposition. This step is similar to the 1D discrete nonsubsampled wavelet transform (NSWT), which uses the à trous method [19]. Compared to NSWT, NSCT uses a nonsubsampled 2D filter. The frame bound of an NSCT directional decomposition is

(2.5)

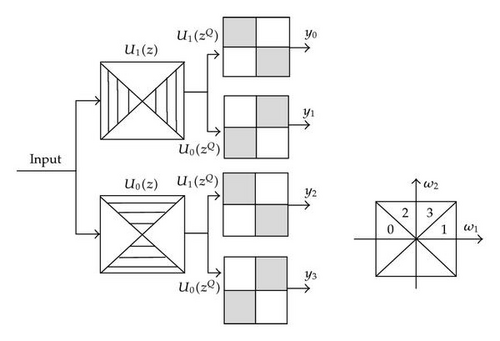
After decomposition of the first layer, the sampling filter banks provide multiscale decomposition of the underlying properties. The process for two-layer nonsubsampled pyramid decomposition is shown in Figure 3.

The frequency domain for layer j supported by a low-pass filter is [−(π/2^j), −(π/2^j)]; the replacement domain is from [−(π/2^j−1), −(π/2^j−1)] to [−(π/2^j), −(π/2^j)], which is supported by a high-pass filter.

Each step in NSWT image decomposition involves three directions. The total image redundancy is 3J + 1; in NSP, the result redundancy is J + 1 [20]. The second NSCT step provides directional information via the nonsubsampled filter, which combines two-channel quincunx sampling filters and a resampling operation for 2D frequency division on directional edges [21]. More accurate directional details can be sampled discretely on a sample stage. Sampling uses a quincunx matrix Q and considers image direction alignment. The process is shown in Figure 4.

3. NLM Filter Based on a Bayesian Approach

3.1. NLM Filter

Different frequency components play different roles in an image structure. Low-frequency components account for most image energy, forming basic local gradation areas, but play a small role in image content or structure. High-frequency components form the main image edges and determine its basic content or structure and are thus the most important components. Changes in high-frequency information lead to changes in the basic image content or structure, and information extracted from the image by the human eye will thus be subject to major changes. Thus, high-frequency components play the most important role in image perception by the human eye.

At present, many image filters only consider adjacent pixels; some filters take into account information for neighboring pixels, such as Yaroslavsky neighborhood filters [22] and bilateral filters [23]. A nonlinear filter involves additive white noise and can effectively handle image redundancy [24].

The NLM algorithm takes advantage of grayscale image redundancy and structural redundancy through a weighted average of pixel values to estimate the current pixel value. The value of each pixel is calculated using the Gaussian-weighted Euclidean distance between subblocks; a pixel as taken as the right center of the corresponding subblock. This ensures that pixels with a similar structure are assigned greater weight. For an original image v = {v(i)∣i ∈ I}, the expression for the image processed using the NLM filter, NL(v), is

(3.1)

where w(i, j) is the Gaussian-weighted Euclidean distance between pixels i and j, which represents the similarity of the image subblocks with i and j as centers:

(3.2)

where Z(i) is a normalization factor, v(N_i) is a set of subblocks with pixel i as the center, ∥·∥_2a is a Gaussian-weighted Euclidean distance function, a is Gaussian kernel standard deviation, and h is a filter parameter that controls the degree of smoothing. The weight w(i, j) meets 0 ≤ w(i, j) ≤ 1, if neighborhood pixels are more similar with v(N_i), the weight of center pixel is greater.

3.2. NLM Filter Combined with a Bayesian Method

The traditional NLM algorithm is very similar in both grayscale and structure content for smooth neighborhood areas. The algorithm yields the best results in flat areas, where better denoising effects can be obtained. At image edges and in texture-rich regions, the algorithm performs poorly because these regions have many repeat structures, the difference in grayscale content is greater, and the larger Euclidean distance makes the weights very small and reduces denoising capability, especially the ability to retain image detail [25]. To improve the edge retention capacity of the NLM algorithm, a Bayesian algorithm was added to make use of image edge information and adjust the similarity of the neighborhood structure so that the center pixel of edge contents that are similar can be given greater weight. This provides a more effective approach for protecting image detail.

The Bayesian NLM filter is expressed as

(3.3)

where v(x) represents noise data, u(x) represents nonnoise image data, n(x) is the average pixel precision weight for gray value u(y) at a rate of change Δx, and p(v(x)∣u(y))p(u(y)) is the similarity between v(x) and u(y). Equation (5) can then be rewritten as

(3.4)

3.3. Improved Bayesian NLM Filter

We propose an improved Bayesian NLM filter in which a sigma range is added to the prior image operation for more effective protection of image details [26]. The first step is analysis of the probability density for pixel levels, which takes the average variance for the improved Bayesian filter. Considering the independence and integrity of an image, its conditional probability distribution can be expressed as

(3.5)

where v_m(x) and u_m(y) are the image probability densities at pixel m and v_m(y) is a subset of u_m(y). For L-level image decomposition, the conditional probability density function is

(3.6)

(3.7)

Because of multiscale features, we assume that the prior probability p(u(y)) is continuous and uniform, p(u(y)) = 1/|Δx|. The proposed algorithm uses an iterative technique, which takes the observed value v(x) as the initial value u(y). This treatment can process data directly but takes longer, and details can become fuzzy. If the frequency window is too large, the result will have too much edge details and point targets become even more blurred. Experimental results confirmed that 3 × 3 window is an appropriate choice. The algorithm uses an a priori estimate mean u’(y) to replace u(y) to reduce image noise bias and Δx is replaced by N(x). The new Bayesian filter can be expressed as

(3.8)

N(x) can be expressed as N(x) = Δx∩N₁(x)∩N₂(x), where N₁(x) and N₂(x) are a priori regional image characteristics and pixel features, respectively. The a priori regional characteristic is image region Δx, and unrelated points are removed using a region similarity algorithm. The a priori pixel feature is the set obtained by comparing the similarity of adjacent pixels [27]. A priori pixel characteristics are generally always overlooked in NLM filter processes. In fact, a priori pixel characteristics are good for excluding pixel noise [28].

The sigma range between pixel x and the a priori mean u’(x) can be defined as (u’(x)I₁, u’(x)I₂) and the range (I₁, I₂) meets , where p(s) is the image probability density function. For different sigma values ξ ∈ {0.1,0.2, …, 0.9}, the range can be calculated by pixel search [29].

It is desirable to have a greater sigma weight; however, under conditional probability, the sigma range cannot be greater than the maximum upper boundary, u’(x)I₂ < V_max, where V_max is the maximum image density. It has been demonstrated that a priori pixel characteristics can have a good effect on retention of image edges, but there will be some situations in which isolated pixels are ignored. To solve this problem, the proposed algorithm uses a threshold T = V_max/2 to separate two pixels [30]. For a priori pixels, only u’(x) < T are retained.

4. Image Feature Extraction Based on the Contourlet Transform

The proposed algorithm can improve the accuracy and completeness of image feature extraction based on direct contourlet decomposition. An image is first processed by the contourlet transform to yield a multidimensional domain, with multiple-resolution decomposition coefficients for large-scale details (low-frequency signal) and finer image details (high-frequency signal). Next, the algorithm applies deeper decomposition to the large-scale approximation. The whole process can be repeated until the algorithm yields the detail required.

Figure 5 shows the two-layer decomposition, where I is the observed image, I’ is the image processed using the contourlet transform, LP is a Laplacian pyramid decomposition filter, DFB is a direction filter bank, LF is the low-frequency signal and HF is the high-frequency signal.

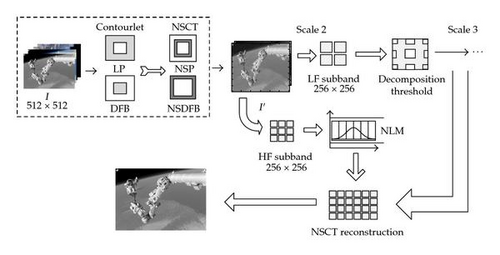
The decomposition coefficients for different frequencies are processed using the Bayesian-based NLM filter with a decomposition threshold. In particular, we use the wavelet threshold approach for the low-frequency part and the NLM approach for the high-frequency part. The specific steps in the algorithm are as follows.

Step 1. Decompose image I using the nonsubsampled contourlet transform.

Step 2. Apply the decomposition threshold method to the low-frequency part for noise suppression and feature extraction.

Step 3. Apply the improved Bayesian NLM filter to the high-frequency part for feature extraction.

Step 4. Reconstruct the high-frequency and low-frequency parts of the image processed using the contourlet transform.

For the low-frequency part, threshold decomposition is used to remove image noise. First, the threshold value T is set. Decomposition coefficients smaller than T are considered to be noise and thus are set to zero; coefficients greater than T are reserved. The decomposition threshold is

(4.1)

where k is the number of layers for wavelet decomposition, θ_n is a function for estimating mean absolute deviation, where d1 is the high-frequency coefficient for first-layer contourlet decomposition. The high-frequency part of the first layer usually contains few signal components and comprises mainly noise. For the high-frequency part, G[D_k(x)] and G[D_k(y)] are two blocks for image I. G [D_k(p)] represents the rectangular neighborhood around p as center. The proposed algorithm uses an improved Bayesian NLM image filter and a Euclidean distance to represent similarity between high-frequency image blocks. The similarity is represented by w(x, y), which is defined as

(4.2)

where h is a constant used to control the exponential decay rate. Compared with the original NLM filter, the contourlet transform decomposes the image at different resolutions and the proposed approach uses different algorithm to process an image: threshold decomposition is used for the low-frequency part, and an improved Bayesian NLM filter is used for the high-frequency part. The NLM filter involves time-consuming calculations. If an image is decomposed by the contourlet transform for k levels, the improved algorithm only has to process 1/2^k of the original size. This not only reduces the computational complexity but also greatly improves the accuracy of feature extraction.

5. Experimental Results

Spatial image can directly influence the success of spatial rendezvous and docking. We must ensure that the most accurate image feature can be extracted from spatial images. The proposed algorithm can also be applied to general image processing. To verify the performance of the algorithm, we carried out experiments both on Spatial images and standard images.

5.1. Performance Evaluation Based on Spatial Images

Tests were carried out on image I and image II for an image size of 512 × 512. Multidimensional contourlet and curvelet decomposition algorithms were used for comparison. The same parameters were used for all algorithms.

Image feature extraction results were evaluated according to subjective and objective standards. Figure 6 shows the processing results for image I, and Figure 7 shows the results for image II. It is evident that the proposed algorithm yields a better subjective visual effect compared with the curvelet and contourlet algorithms.

The results show that feature extraction with the curvelet transform leads to confusion for some background information, and the contourlet transform yields a blurry image. By contrast, the proposed algorithm effectively suppresses noise and displays the main features of the image. Finer image details are shown in Figure 8.

5.2. Performance Evaluation Based on Standard Images

Figures 9 and 10 show the processing results for image as III, IV. Image as III and IV are standard images for an image size of 512 × 512. It is shown that our algorithm also provides better performance than that of Curvelet transform and Contourlet transform.

Results are objectively evaluated using the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM), defined as follows:

(5.1)

where u_x and u_y are the mean and σ_x and σ_y are the standard deviation for the original and processed images, respectively, σ_xy is the covariance for the original and processed images, and C₁ and C₂ are constants. MSSIM is mean SSIM, and W is the number of image subblocks. For greater PSNR and MSSIM (0 ≤ MSSIM ≤ 1), the processed image is closer to the original.

Table 1 compares the feature extraction performance for images I and II for several algorithms and different noise levels. The PSNR results show that the contourlet transform is superior to the curvelet transform for image I by almost 0.5 dB. Both the contourlet and curvelet transforms provide good edge detection. The proposed CT + NLM algorithm showed even better performance (~1.1 dB) compared with the contourlet transform but retained the good edge detection of the latter method (Table 1).The proposed algorithm uses an NLM filter for adaptive image expression. The MSSIM results show that the proposed algorithm yields the best performance for Gaussian, Poisson, Salt and Pepper and Speckle noise (Table 2).

Table 1. PSNR results.

Noise σ				PSNR (dB)
Noise σ		Noisy	Original	Curvelet	Contourlet	CT + NLM
10	Image I	31.22	32.93	33.01	33.58	34.62
10	Image II	32.98	33.53	33.89	34.21	35.40
20	Image I	31.16	31.89	32.75	33.01	34.19
20	Image II	32.49	33.14	33.19	33.82	34.89
30	Image I	30.78	31.56	32.13	32.78	33.76
30	Image II	31.98	32.75	32.82	33.21	34.17
40	Image I	30.56	31.01	31.74	32.53	33.61
40	Image II	31.20	32.11	32.42	32.91	33.98
50	Image I	29.88	30.54	31.29	31.74	32.83
50	Image II	30.77	31.56	31.98	32.17	33.28

Table 2. MSSIM results.

Noise				MSSIM
Noise		Noisy	Original	Curvelet	Contourlet	CT + NLM
Gaussian	Image I	0.2979	0.3128	0.3524	0.4277	0.5185
Gaussian	Image II	0.3014	0.3256	0.3688	0.4316	0.5220
Poisson	Image I	0.5744	0.6231	0.6827	0.7173	0.8219
Poisson	Image II	0.5891	0.6349	0.7028	0.7339	0.8551
Salt and pepper	Image I	0.2948	0.3239	0.3740	0.4157	0.5255
Salt and pepper	Image II	0.3001	0.3398	0.3829	0.4254	0.5345
Speckle	Image I	0.2953	0.3321	0.3974	0.4309	0.5312
Speckle	Image II	0.3021	0.3476	0.4012	0.4452	0.5422

Our algorithm uses a nonsubsampled key point filter for which J + 1 redundancy is the most efficient. In pyramid decomposition, a lesser extent of image loss can be considered as an effective means to reduce redundancy. The proposed algorithm, which uses a nonsubsampled pyramid filter and a directional filter, leads to some image loss in reducing redundancy. Search windows of 16 × 16, 32 × 32, and 64 × 64 were applied to images I and II. The size of the search window can affect the computational complexity of the NLM filter.

Comparison of the experimental results for different window sizes reveals that the proposed algorithm delivers better noise suppression and feature extraction than the other algorithms. It provides a maximum PSNR value and a minimum MSSIM value for all windows (Table 3).

Table 3. Experimental results for different search windows.

Scheme	Search window 16 × 16				Search window 32 × 32				Search window 64 × 64
	Image I		Image II		Image I		Image II		Image I		Image II
	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM	PSNR	SSIM
Original	30.53	0.658	31.45	0.679	30.09	0.669	31.21	0.685	29.89	0.675	31.09	0.703
Curvelet	30.78	0.697	31.66	0.722	30.12	0.701	31.39	0.737	29.91	0.688	31.15	0.749
Contourlet	31.23	0.759	31.98	0.784	30.35	0.762	31.65	0.791	30.17	0.744	31.23	0.806
CT + NLM	32.38	0.783	32.89	0.802	31.37	0.788	32.68	0.811	31.23	0.796	32.22	0.835

6. Conclusions

Focusing on the actual needs of spatial images analysis, an improved contourlet transform, consisting of a nonsubsampled pyramid transform and nonsubsampled directional filter banks, was used to reduce the filter design problem of spatial images. The improved contourlet transform uses a mapping approach to solve the 2D filter design problem. The algorithm uses a Bayesian NLM filter for high-frequency information to suppress noise and improve the accuracy of image feature extraction. Experimental results confirm that the NLM filter can effectively retain structural information and reduce the residual structure. In the NSCT domain, the proposed algorithm showed better denoising and enhancement effects compared with the contourlet transform. Moreover, in comparison with NSWT, the algorithm is a more mature and sophisticated image-processing method.

Acknowledgments

This work was supported by the National Basic Research Program of China (973 Program) (2012CB821206), the National Natural Science Foundation of China (no. 91024001, no. 61070142), and the Beijing Natural Science Foundation (no. 4111002).

References

1 Liu P., Huang F., Li G., and Liu Z., Remote-sensing image denoising using partial differential equations and auxiliary images as priors, IEEE Geoscience and Remote Sensing Letters. (2012) 9, no. 3, 358–362, 6061940, https://doi.org/10.1109/LGRS.2011.2168598.
10.1109/LGRS.2011.2168598
Web of Science® Google Scholar
2 Demirel H. and Anbarjafari G., Discrete wavelet transform-based satellite image resolution enhancement, IEEE Transactions on Geoscience and Remote Sensing. (2011) 49, no. 6, 1997–2004, 2-s2.0-79957650213, https://doi.org/10.1109/TGRS.2010.2100401.
10.1109/TGRS.2010.2100401
Web of Science® Google Scholar
3 Pan P. and Schonfeld D., Image reconstruction and multidimensional field estimation from randomly scattered sensors, IEEE Transactions on Image Processing. (2008) 17, no. 1, 94–99, https://doi.org/10.1109/TIP.2007.912579, 2439795.
10.1109/TIP.2007.912579
PubMed Web of Science® Google Scholar
4 Kamalabadi F., Multidimensional image reconstruction in astronomy, IEEE Signal Processing Magazine. (2010) 27, no. 1, 86–96, 2-s2.0-72849137612, https://doi.org/10.1109/MSP.2009.934717.
10.1109/MSP.2009.934717
Web of Science® Google Scholar
5 Mahmoudi M. and Sapiro G., Fast image and video denoising via nonlocal means of similar neighborhoods, IEEE Signal Processing Letters. (2005) 12, no. 12, 839–842, 2-s2.0-29144467969, https://doi.org/10.1109/LSP.2005.859509.
10.1109/LSP.2005.859509
Web of Science® Google Scholar
6 Buades A., Coll B., and Morel J. M., A review of image denoising algorithms, with a new one, Multiscale Modeling & Simulation. (2005) 4, no. 2, 490–530, https://doi.org/10.1137/040616024, 2162865, ZBL1108.94004.
10.1137/040616024
Web of Science® Google Scholar
7 Donoho D. L., Vetterli M., DeVore R. A., and Daubechies I., Data compression and harmonic analysis, IEEE Transactions on Information Theory. (1998) 44, no. 6, 2435–2476, https://doi.org/10.1109/18.720544, 1658775, ZBL1125.94311.
10.1109/18.720544
Web of Science® Google Scholar
8 Mallat S., A Wavelet Tour of Signal Processing, 2009, 3rd edition, Elsevier/Academic Press, Amsterdam, The Netherlands, 2479996.
Google Scholar
9 Candès E. J. and Donoho D. L., A. Cohen, C. Rabut, and L.L. Schumaker, Curvelets—a surprisingly effective nonadaptive representation for objects with edges, Curve and Surface Fitting, 1999, Vanderbilt University Press, Nashville, Tenn, USA, 105–120.
Google Scholar
10 Candès E. J. and Donoho D. L., New tight frames of curvelets and optimal representations of objects with piecewise C² singularities, Communications on Pure and Applied Mathematics. (2004) 57, no. 2, 219–266, https://doi.org/10.1002/cpa.10116, 2012649.
10.1002/cpa.10116
Web of Science® Google Scholar
11 Do M. N. and Vetterli M., The contourlet transform: an efficient directional multiresolution image representation, IEEE Transactions on Image Processing. (2005) 14, no. 12, 2091–2106, 2-s2.0-28944432472, https://doi.org/10.1109/TIP.2005.859376.
10.1109/TIP.2005.859376
PubMed Web of Science® Google Scholar
12 Burt P. J. and Adelson E. H., The Laplacian pyramid as a compact image code, IEEE Transactions on Communications. (1983) 31, no. 4, 532–540, 2-s2.0-0020737631, https://doi.org/10.1109/TCOM.1983.1095851.
10.1109/TCOM.1983.1095851
CAS Web of Science® Google Scholar
13 Do M. N. and Vetterli M., Framing pyramids, IEEE Transactions on Signal Processing. (2003) 51, no. 9, 2329–2342, https://doi.org/10.1109/TSP.2003.815389, 2004247.
10.1109/TSP.2003.815389
Web of Science® Google Scholar
14 Bamberger R. H. and Smith M. J. T., A filter bank for the directional decomposition of images: theory and design, IEEE Transactions on Signal Processing. (1992) 40, no. 4, 882–893, 2-s2.0-0026847407, https://doi.org/10.1109/78.127960.
10.1109/78.127960
Web of Science® Google Scholar
15 Eslami R. and Radha H., Translation-invariant contourlet transform and its application to image denoising, IEEE Transactions on Image Processing. (2006) 15, no. 11, 3362–3374, 2-s2.0-33750379296, https://doi.org/10.1109/TIP.2006.881992.
10.1109/TIP.2006.881992
PubMed Web of Science® Google Scholar
16 Po D. D.-Y. and Do M. N., Directional multiscale modeling of images using the contourlet transform, IEEE Transactions on Image Processing. (2006) 15, no. 6, 1610–1620, https://doi.org/10.1109/TIP.2006.873450, 2478998.
10.1109/TIP.2006.873450
PubMed Web of Science® Google Scholar
17 da Cunha A. L., Zhou J., and Do M. N., The nonsubsampled contourlet transform: theory, design, and applications, IEEE Transactions on Image Processing. (2006) 15, no. 10, 3089–3101, 2-s2.0-33749161371, https://doi.org/10.1109/TIP.2006.877507.
10.1109/TIP.2006.877507
PubMed Web of Science® Google Scholar
18 McClellan J. H., The design of two-dimensional digital filters by transformation, Proceedings of the 7th Annual Princeton Conference on Information Sciences and Systems, 2003, 247–251.
Google Scholar
19 Shensa M. J., The discrete wavelet transform: wedding the atrous and Mallat algorithms, IEEE Transactions on Signal Processing. (1992) 40, no. 10, 2464–2482, 2-s2.0-0026938667, https://doi.org/10.1109/78.157290.
10.1109/78.157290
Web of Science® Google Scholar
20 Bamberger R. H. and Smith M. J. T., A filter bank for the directional decomposition of images: theory and design, IEEE Transactions on Signal Processing. (1992) 40, no. 4, 882–893, 2-s2.0-0026847407, https://doi.org/10.1109/78.127960.
10.1109/78.127960
Web of Science® Google Scholar
21 Simoncelli E. P., Freeman W. T., Adelson E. H., and Heeger D. J., Shiftable multiscale transforms, IEEE Transactions on Information Theory. (1992) 38, no. 2, 587–607, https://doi.org/10.1109/18.119725, 1162216.
10.1109/18.119725
Web of Science® Google Scholar
22 Tasdizen T., Principal neighborhood dictionaries for nonlocal means image denoising, IEEE Transactions on Image Processing. (2009) 18, no. 12, 2649–2660, https://doi.org/10.1109/TIP.2009.2028259, 2724813.
10.1109/TIP.2009.2028259
PubMed Web of Science® Google Scholar
23 Orchard J., Ebrahimi M., and Wong A., Efficient nonlocal-means denoising using the SVD, IEEE International Conference on Image Processing (ICIP ′08), October 2008, 1732–1735, 2-s2.0-69949169668, https://doi.org/10.1109/ICIP.2008.4712109.
10.1109/ICIP.2008.4712109
Google Scholar
24 Dowson N. and Salvado O., Hashed nonlocal means for rapid image filtering, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2011) 33, no. 3, 485–499, 2-s2.0-79551535890, https://doi.org/10.1109/TPAMI.2010.114.
10.1109/TPAMI.2010.114
PubMed Web of Science® Google Scholar
25 Protter M., Elad M., Takeda H., and Milanfar P., Generalizing the nonlocal-means to super-resolution reconstruction, IEEE Transactions on Image Processing. (2009) 18, no. 1, 36–51, https://doi.org/10.1109/TIP.2008.2008067, 2741734.
10.1109/TIP.2008.2008067
PubMed Web of Science® Google Scholar
26 Coupé P., Hellier P., Kervrann C., and Barillot C., Nonlocal means-based speckle filtering for ultrasound images, IEEE Transactions on Image Processing. (2009) 18, no. 10, 2221–2229, https://doi.org/10.1109/TIP.2009.2024064, 2814613.
10.1109/TIP.2009.2024064
PubMed Web of Science® Google Scholar
27 Zeng W. L. and Lu X. B., Region-based non-local means algorithm for noise removal, Electronics Letters. (2011) 47, no. 20, 1125–1127, https://doi.org/10.1049/el.2011.2456.
10.1049/el.2011.2456
Web of Science® Google Scholar
28 Zhong H., Li Y., and Jiao L., SAR image despeckling using bayesian nonlocal means filter with sigma preselection, IEEE Geoscience and Remote Sensing Letters. (2011) 8, no. 4, 809–813, 2-s2.0-79959715322, https://doi.org/10.1109/LGRS.2011.2112331.
10.1109/LGRS.2011.2112331
Web of Science® Google Scholar
29 Lai R. and Yang Y. T., Accelerating non-local means algorithm with random projection, Electronics Letters. (2011) 47, no. 3, 182–183, 2-s2.0-79551705195, https://doi.org/10.1049/el.2010.2618.
10.1049/el.2010.2618
Web of Science® Google Scholar
30 Thacker N. A., Manjon J. V., and Bromiley P. A., Statistical interpretation of non-local means, IET Computer Vision. (2010) 4, no. 3, 162–172, https://doi.org/10.1049/iet%2Dcvi.2008.0076, 2761197.
10.1049/iet-cvi.2008.0076
Web of Science® Google Scholar

Citing Literature

All articles

Spatial Images Feature Extraction Based on Bayesian Nonlocal Means Filter and Improved Contourlet Transform

Abstract

1. Introduction

2. Contourlet Transform Decomposition