Volume 2012, Issue 1 457121

Research Article

Open Access

Necessary Optimality Conditions for a Class of Impulsive and Switching Systems

Lihua Li,

Corresponding Author

Lihua Li

[email protected]

School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China usst.edu.cn

School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai 200090, China shiep.edu.cn

Search for more papers by this author

Yan Gao,

Yan Gao

School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China usst.edu.cn

Search for more papers by this author

Gexia Wang,

Gexia Wang

School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai 200090, China shiep.edu.cn

Search for more papers by this author

Lihua Li,

Corresponding Author

Lihua Li

[email protected]

School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China usst.edu.cn

School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai 200090, China shiep.edu.cn

Search for more papers by this author

Yan Gao,

Yan Gao

School of Management, University of Shanghai for Science and Technology, Shanghai 200093, China usst.edu.cn

Search for more papers by this author

Gexia Wang,

Gexia Wang

School of Mathematics and Physics, Shanghai University of Electric Power, Shanghai 200090, China shiep.edu.cn

Search for more papers by this author

First published: 13 October 2012

https://doi.org/10.1155/2012/457121

Citations: 1

Academic Editor: Piyapong Niamsup

Share a link

Email
Wechat
Bluesky

Abstract

An optimal control problem for a class of hybrid impulsive and switching systems is considered. By defining switching times as part of extended state, we get the necessary optimality conditions for this problem. It is shown that the adjoint variables satisfy certain jump conditions and the Hamiltonian are continuous at switching instants. In addition, necessary optimality conditions of Fréchet subdifferential form are presented in this paper.

1. Introduction

In a broad sense, hybrid systems are control systems involving both continuous and discrete variables. Much attention has been paid on the control of hybrid systems in recent years, see [1–27] and references therein. Impulsive and switching systems are a particular class of hybrid systems characterized by switches of states and abrupt changes at the switching instants. Many real-world processes such as evolutionary processes, flying object motions, signal processing systems, and so forth, can be modeled as impulsive and switching systems. Therefore, it is important to study the properties of this kind of systems. In [1], by using switched Lyapunov functions, Guan et al. gave some general criteria for exponential stability and asymptotic stability of some impulsive and switching models. The robust stability conditions for several types of impulsive switching systems were presented in [2–5]. Sufficient conditions for exponential stability and input-to-state stability of nonlinear impulsive switched systems were established in [6, 7]. All of these papers concentrated on the stability of impulsive and switching systems.

Over the last few decades, there have been a large number of researches on optimal control of hybrid systems. Different approaches have been proposed in this fields, such as the viscosity solution technique [8], dynamic programming methods [9–11], the embedding approach [12], direct differentiation of the cost function [13–15], necessary optimality conditions [16–24] and the method of smoothed approximation [25].

In [26], Gao et al. investigated optimal control problem for a class of impulsive and switching systems, where the impulses and switches occurred at fixed instants. Taking advantage of Ekeland’s variational principle, they obtained the necessary optimality conditions for the continuous parts. In this paper, we consider similar problems with unfixed impulsive and switching instants. By introducing a new time variable, we get necessary optimality conditions for the continuous parts and the switching instants. Compared with the continuous parts, the necessary conditions at the switching times is more challenging and difficult to obtain. Furthermore, by applying Fréchet subdifferential, we give necessary optimality conditions with nonsmooth cost functional. Usually, the advantage of hybrid system lies in its nonsmooth trajectory. Therefore, the use of nonsmooth objective functional can reflect this advantage better.

The rest of the paper is organized as follows. In Section 2, the problem is formulated. In Section 3, necessary optimality conditions with smooth and nonsmooth cost functional are presented. Section 4 concludes the work.

2. Problem Formulation

Consider the following controlled nonlinear systems in fixed time interval [t₀, t_N]:

(2.1)

where x(t) ∈ ℝⁿ is the state, u(t) ∈ Ω is a piecewise continuous control input, Ω is a bounded and convex set in ℝ^m, f is twice continuous differentiable with their variables. v(t, x) is a hybrid impulsive and switching control, which can be described as follows:

(2.2)

where B_1i, B_2i are n × n constant matrices, δ(·) is the Dirac impulse and

(2.3)

Here we suppose t₁ < t₂ < ⋯<t_N−1 are unfixed points.

Let the state of (2.1) is left continuous,

. Denote

, A_i = A + B_1i and B_i = B_2i, then under the control of (2.2), the nonlinear system (2.1) can be expressed as follows:

(2.4)

In addition, we suppose that the system (2.4) satisfies

and g(x(t_N)) = 0.

Now we give the following optimal control problem (P): for impulsive switching systems (2.4), find impulsive switching instants t_i, i = 1, …, N − 1, and a piecewise continuous input u(t), such that the cost functional

(2.5)

is minimized, where φ_i denote the switching cost, i = 1, …, N − 1, L describes the operating cost of the continuous parts and φ_N denotes the cost relative to the terminal state. All of these functions are twice continuous differentiable with their variables.

Optimal control problem for (2.4) was considered in [26], where the switching instants were fixed. In this paper, we consider such a problem with unfixed switching times, which is more flexible in practical applications.

To this end, let (x⁰, u⁰) be a solution of problem (P) with a piecewise continuous control function u⁰.

3. Necessary Conditions of Optimality with Smooth Cost Functional

Now we give a necessary condition for problem (P).

Theorem 3.1. There exist a piecewise continuously differential variable λ(t):[t₀, t_N] → ℝⁿ, multipliers μ ∈ ℝ and λ₀ ∈ ℝ, such that (x⁰, u⁰) satisfies

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

where H(x, u, λ) = λ₀L(x, u) + λ^T[A_ix + f(x, u)].

Proof. For i = 1, …, N, define

(3.6)

with a new time variables s ∈ [0,1], then problem (P) can be reformulated as the following classical problem (Q): minimize

(3.7)

subject to

(3.8)

The Hamiltonian of problem (Q) is denoted by .

Applying classical necessary optimality conditions to problem (R), there exist λ_i(s) ∈ ℝⁿ, i = 1, …, N, , i = 1, …, N − 1, ξ_i ∈ ℝ and ω_i ∈ ℝⁿ, i = 1, …, N − 1, such that for

(3.9)

we have

(3.10)

(3.11)

(3.12)

(3.13)

(3.14)

(3.15)

(3.16)

(3.17)

For autonomous system, the Hamiltonian is constant along the optimal trajectory, so the right hand of (3.11) is constant on [0,1]. Combining (3.11) with the boundary conditions (3.15) and (3.16), We get the continuity condition (3.4).

Recombine the adjoint variable

(3.18)

we get (3.1) from (3.10). (3.2) and (3.3) come from (3.14) and (3.20), respectively. (3.12) and (3.13) result in the jump condition (3.5) by eliminating ω_i. The proof of the theorem is completed.

Remark 3.2. Besides the necessary optimality conditions for the continuous parts and the terminal costate, which were derived in [26], Theorem 3.1 also give the necessary optimality conditions for the switching instants. Therefore, Theorem 3.1 is an important improvement and generalization of the main results in [26].

Example 3.3. Minimize the cost functional

(3.19)

subject to

(3.20)

where 0 ≤ u ≤ 1.

For t ∈ [0, t₁], we deduce that λ(t) = c₁e^t + 1 by (3.1). Denote H = x(t) − 2u(t) + λ(t)(−x(t) + u(t)), taking advantage of (3.3), we get that

(3.21)

where c₁ is a constant in ℝ.

In addition, by

and x(0) = 2, we obtain that

(3.22)

where t_s is the root of c₁e^t = 1.

Similarly, we can get the equations for the control, adjoint and state variable for t ∈ (t₁, 2]. By (3.4), we get that

(3.23)

After some calculation, we obtain four equations by (3.5), (3.23),

, and

. By MatLab procedure and Newton methods of solving nonlinear equations, we get that the impulsive and switching time is t₁ = 1.1595 and the control variables is

(3.24)

The behavior of control, adjoint and state variable is shown in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Control, adjoint, and state variable in the Example 3.3.

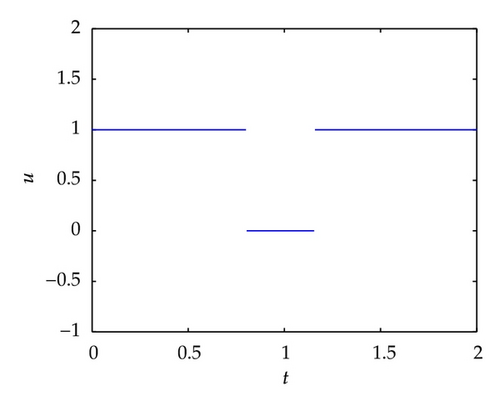
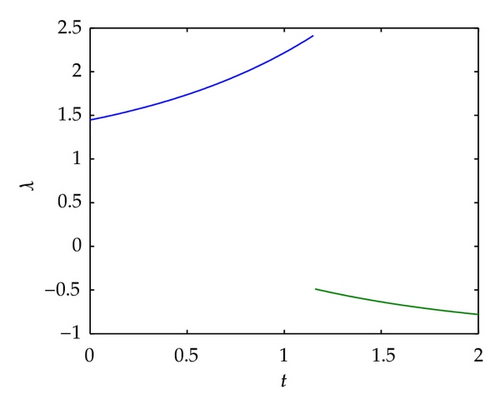
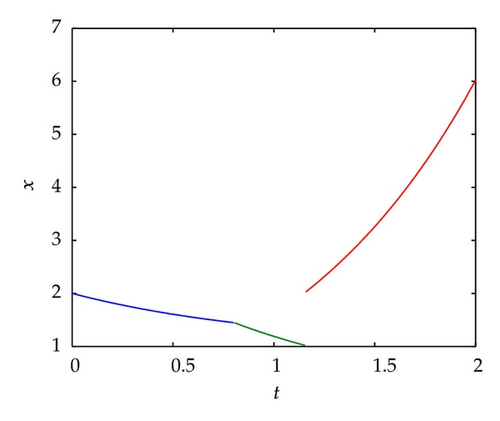
4. Necessary Optimality Conditions with Nonsmooth Cost Functional

To establish superdifferential form of necessary optimality conditions, we shall introduce some basic knowledge of nonsmooth analysis. For more knowledge, the reader can refer to [18, 28].

Given a nonempty set Ω ∈ ℝⁿ and

, the prenormal cone to Ω at

is defined by the following:

(4.1)

, put

Let epi φ = {(x, α) ∈ ℝⁿ⁺¹∣α ≥ φ(x)}, if φ is lower semicontinuous, the Fréchet subdifferential of φ at

is expressed in geometric form

(4.2)

Similarly, if φ is supper semicontinuous, we can define the Fréchet supperdifferential of φ at by . For example, let φ(x) = |x|, then and .

If φ is continuous, the Fréchet differential of φ at

is defined by

(4.3)

Lemma 4.1 (see [18], [28].)Let φ : X → ℝ, . Then for any , there exists a function s : X → ℝ with and s(x) ≤ φ(x) whenever x ∈ X, such that s(·) is Fréchet differentiable at with .

Theorem 4.2. Let (x⁰, u⁰) be a weak local minimum of problem (P), φ_i is Fréchet subdifferentiable at x⁰(t_i), then for every , i = 1,2, …, N, the results of Theorem 3.1 hold except that (3.1) and (3.4) are replaced by the following:

(4.4)

(4.5)

Proof. For any , taking advantage of Lemma 4.1, there exist functions s_i, such that they are Fréchet differentiable at and the following conditions are satisfied: , , and s_i(x(t_i)) = φ_i(x(t_i)) in some neighborhood of , i = 1, …, N. Therefore (τ⁰, x⁰, u⁰) is a weak local minimum of problem (P3): Minimize the functional

(4.6)

subject to (2.4). Combining the results of Lemma 4.1 and Theorem 3.1, we complete the proof of the theorem.

Example 4.3. Minimize the cost functional

(4.7)

subject to

(4.8)

where −1 ≤ u ≤ 1.

By (4.5), we have

(4.9)

where d ∈ [−1,1] is Fréchet subdifferential at the switching point.

Taking advantage of similar method in Example 3.3, we get that the optimal impulsive switching time is 1.4169 and the control variables is

(4.10)

The behavior of control, adjoint and state variable is shown in Figure 2.

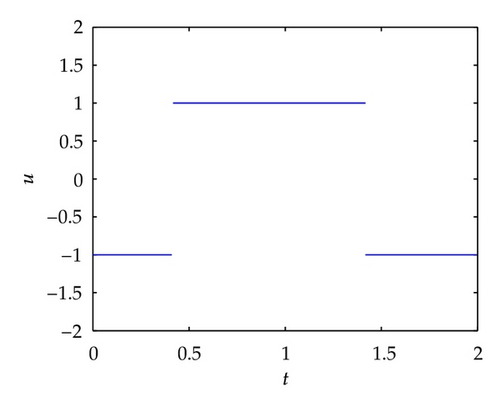
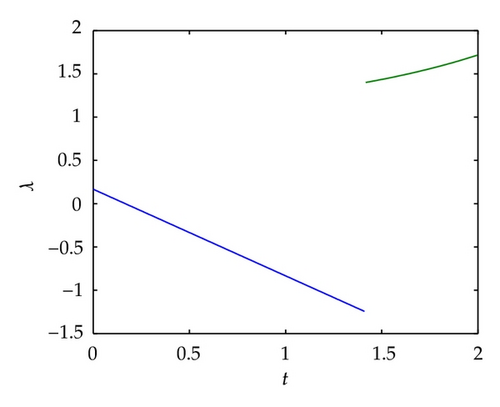
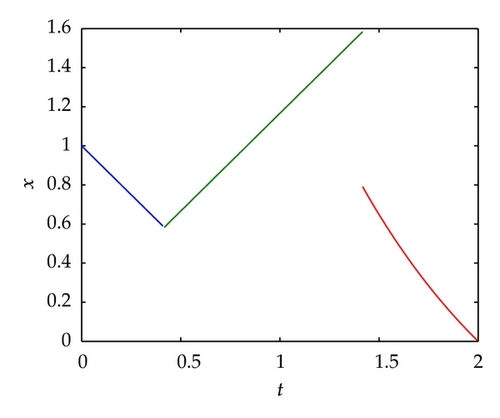
Remark 4.4. As shown in Example 4.3, the necessary optimality condition of Fréchet subdifferential form allows us to get the optimal switching point for the problem with nonsmooth cost functional, but the usual necessary optimality conditions fails to do this.

5. Conclusions

In this paper, we have investigated optimal control problems for a class of impulsive and switching systems, where the switching transitions are unfixed. By defining the switching instants as part of extended state and taking advantage of the knowledge of nonsmooth analysis, the necessary optimality conditions with both smooth cost functional and nonsmooth cost functional are derived, which are the substantial extension and generalization of some known results in the literature.

Acknowledgments

This work is supported by National Science Foundation of China (no. 11171221), Science and Technology Commission of Shanghai Municipality (no. 10550500800), and Shanghai Education Foundation for Innovational Scientific Research Foundation (no. 11YZ193).

References

1 Guan Z.-H., Hill D. J., and Shen X., On hybrid impulsive and switching systems and application to nonlinear control, IEEE Transactions on Automatic Control. (2005) 50, no. 7, 1058–1062, https://doi.org/10.1109/TAC.2005.851462, 2151574.
10.1109/TAC.2005.851462
Web of Science® Google Scholar
2 Zong G., Wu Y., Zhang B., and Kong Y., Robust exponential stability of uncertain discrete time impulsive switching systems with state delay, Journal of Control Theory and Applications. (2007) 5, no. 4, 351–356, https://doi.org/10.1007/s11768%2D006%2D6051%2Dx, 2370478, ZBL1150.93536.
10.1007/s11768-006-6051-x
Google Scholar
3 Xu H., Teo K. L., and Liu X., Robust stability analysis of guaranteed cost control for impulsive switched systems, IEEE Transactions on Systems, Man, and Cybernetics B. (2008) 38, no. 5, 1419–1422.
10.1109/TSMCB.2008.925747
PubMed Web of Science® Google Scholar
4 Zhang Z. and Liu X., Robust stability of uncertain discrete impulsive switching systems, Computers & Mathematics with Applications. (2009) 58, no. 2, 380–389, https://doi.org/10.1016/j.camwa.2009.03.099, 2535805, ZBL1189.39027.
10.1016/j.camwa.2009.03.099
Web of Science® Google Scholar
5 Yao J., Guan Z.-H., Chen G., and Ho D. W. C., Stability, robust stabilization and H_∞ control of singular-impulsive systems via switching control, Systems & Control Letters. (2006) 55, no. 11, 879–886, https://doi.org/10.1016/j.sysconle.2006.05.002, 2260773, ZBL1113.93096.
10.1016/j.sysconle.2006.05.002
Web of Science® Google Scholar
6 Xu H. and Teo K. L., Exponential stability with L₂-gain condition of nonlinear impulsive switched systems, IEEE Transactions on Automatic Control. (2010) 55, no. 10, 2429–2433, https://doi.org/10.1109/TAC.2010.2060173, 2742241.
10.1109/TAC.2010.2060173
Web of Science® Google Scholar
7 Liu J., Liu X., and Xie W. C., Class-𝒦ℒ estimates and input-to-state stability analysis of impulsive switched systems, Systems & Control Letters. (2012) 61, no. 6, 738–746.
10.1016/j.sysconle.2012.03.007
Web of Science® Google Scholar
8 Capuzzoi I. D. and Evans L. C., Optimal switching for ordinary differential equations, SIAM Journal on Control and Optimization. (1984) 22, no. 1, 143–161, 2-s2.0-0021202882, https://doi.org/10.1137/0322011.
10.1137/0322011
Web of Science® Google Scholar
9 Borrelli F., Baotić M., Bemporad A., and Morari M., Dynamic programming for constrained optimal control of discrete-time linear hybrid systems, Automatica. (2005) 41, no. 10, 1709–1721, https://doi.org/10.1016/j.automatica.2005.04.017, 2169342, ZBL1125.49310.
10.1016/j.automatica.2005.04.017
Web of Science® Google Scholar
10 Seatzu C., Corona D., Giua A., and Bemporad A., Optimal control of continuous-time switched affine systems, IEEE Transactions on Automatic Control. (2006) 51, no. 5, 726–741, https://doi.org/10.1109/TAC.2006.875053, 2232596.
10.1109/TAC.2006.875053
Web of Science® Google Scholar
11 Rungger M. and Stursberg O., A numerical method for hybrid optimal control based on dynamic programming, Nonlinear Analysis. (2011) 5, no. 2, 254–274, https://doi.org/10.1016/j.nahs.2010.09.002, 2793015, ZBL1225.49028.
10.1016/j.nahs.2010.09.002
Google Scholar
12 Bengea S. C. and DeCarlo R. A., Optimal control of switching systems, Automatica. (2005) 41, no. 1, 11–27, https://doi.org/10.1016/j.automatica.2004.08.003, 2157228, ZBL1088.49018.
10.1016/j.automatica.2004.08.003
Web of Science® Google Scholar
13 Egerstedt M., Wardi Y., and Axelsson H., Transition-time optimization for switched-mode dynamical systems, IEEE Transactions on Automatic Control. (2006) 51, no. 1, 110–115, https://doi.org/10.1109/TAC.2005.861711, 2192797.
10.1109/TAC.2005.861711
Web of Science® Google Scholar
14 Axelsson H., Wardi Y., Egerstedt M., and Verriest E. I., Gradient descent approach to optimal mode scheduling in hybrid dynamical systems, Journal of Optimization Theory and Applications. (2008) 136, no. 2, 167–186, https://doi.org/10.1007/s10957%2D007%2D9305%2Dy, 2372948, ZBL1141.49021.
10.1007/s10957-007-9305-y
Web of Science® Google Scholar
15 Kamgarpour M. and Tomlin C., On optimal control of non-autonomous switched systems with a fixed mode sequence, Automatica. (2012) 48, no. 6, 1177–1181.
10.1016/j.automatica.2012.03.019
Web of Science® Google Scholar
16 Xu X. and Antsaklis P. J., Optimal control of switched systems based on parameterization of the switching instants, IEEE Transactions on Automatic Control. (2004) 49, no. 1, 2–16, https://doi.org/10.1109/TAC.2003.821417, 2028538.
10.1109/TAC.2003.821417
Web of Science® Google Scholar
17 Attia S. A., Azhmyakov V., and Raisch J., On an optimization problem for a class of impulsive hybrid systems, Discrete Event Dynamic Systems. (2010) 20, no. 2, 215–231, https://doi.org/10.1007/s10626%2D009%2D0068%2D5, 2609675, ZBL1197.49038.
10.1007/s10626-009-0068-5
Web of Science® Google Scholar
18 Maharramov S. F., Necessary optimality conditions for switching control problems, Journal of Industrial and Management Optimization. (2010) 6, no. 1, 479–455, https://doi.org/10.3934/jimo.2010.6.47, 2563876, ZBL1183.49020.
10.3934/jimo.2010.6.47
Web of Science® Google Scholar
19 Garavello M. and Piccoli B., Hybrid necessary principle, SIAM Journal on Control and Optimization. (2005) 43, no. 5, 1867–1887, https://doi.org/10.1137/S0363012903416219, 2137505, ZBL1084.49021.
10.1137/S0363012903416219
Web of Science® Google Scholar
20 Shaikh M. S. and Caines P. E., On the hybrid optimal control problem: theory and algorithms, IEEE Transactions on Automatic Control. (2007) 52, no. 9, 1587–1603, https://doi.org/10.1109/TAC.2007.904451, 2352436.
10.1109/TAC.2007.904451
Web of Science® Google Scholar
21 Oberle H. J. and Rosendahl R., Numerical computation of a singular-state subarc in an economic optimal control model, Optimal Control Applications & Methods. (2006) 27, no. 4, 211–235, https://doi.org/10.1002/oca.775, 2253623.
10.1002/oca.775
Web of Science® Google Scholar
22 Dmitruk A. V. and Kaganovich A. M., The hybrid maximum principle is a consequence of Pontryagin maximum principle, Systems & Control Letters. (2008) 57, no. 11, 964–970, https://doi.org/10.1016/j.sysconle.2008.05.006, 2459246, ZBL1151.49017.
10.1016/j.sysconle.2008.05.006
Web of Science® Google Scholar
23 Sussmann H. J., Maximum principle for hybrid optimal control problems, Proceedings of the 38th IEEE Conference on Decision and Control (CDC ′99), December 1999, Phoenix, Ariz, USA, 425–430, 2-s2.0-0033330266, https://doi.org/10.1016/j.sysconle.2007.10.005.
10.1016/j.sysconle.2007.10.005
Google Scholar
24 Mordukhovich B. S. and Shvartsman I., Discrete maximum principle for nonsmooth optimal control problems with delays, Cybernetics and Systems Analysis. (2002) 38, no. 2, 255–264.
10.1023/A:1016399530185
Google Scholar
25 Stewart D. E. and Anitescu M., Optimal control of systems with discontinuous differential equations, Numerische Mathematik. (2010) 114, no. 4, 653–695, https://doi.org/10.1007/s00211%2D009%2D0262%2D2, 2586004, ZBL1183.49032.
10.1007/s00211-009-0262-2
Web of Science® Google Scholar
26 Gao R., Liu X., and Yang J., On optimal control problems of a class of impulsive switching systems with terminal states constraints, Nonlinear Analysis. (2010) 73, no. 7, 1940–1951, https://doi.org/10.1016/j.na.2010.05.013, 2674174, ZBL1201.49041.
10.1016/j.na.2010.05.013
Web of Science® Google Scholar
27 Dong Y., Robust stability analysis for uncertain switched discrete-time systems, Journal of Applied Mathematics. (2011) 2011, 20, 523020, https://doi.org/10.1155/2011/523020, 2854968, ZBL1235.93185.
10.1155/2011/523020
Google Scholar
28 Mordukhovich B. S., Variational Analysis and Generalized Difierentiation, 2004, Springer, Berlin, Germany.
Google Scholar

Citing Literature

All articles

Necessary Optimality Conditions for a Class of Impulsive and Switching Systems

Abstract

1. Introduction

2. Problem Formulation

3. Necessary Conditions of Optimality with Smooth Cost Functional

4. Necessary Optimality Conditions with Nonsmooth Cost Functional

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Necessary Optimality Conditions for a Class of Impulsive and Switching Systems

Abstract

1. Introduction

2. Problem Formulation

3. Necessary Conditions of Optimality with Smooth Cost Functional

4. Necessary Optimality Conditions with Nonsmooth Cost Functional

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information