Volume 2012, Issue 1 451927

Research Article

Open Access

Identification of Hysteresis in Human Meridian Systems Based on NARMAX Model

Yonghong Tan

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Ruili Dong,

Corresponding Author

Ruili Dong

[email protected]

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Hui Chen,

Hui Chen

School of Automation, Southeast University, 2 Sipailou, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

Hong He,

Hong He

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Yonghong Tan,

Yonghong Tan

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Ruili Dong,

Corresponding Author

Ruili Dong

[email protected]

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

Hui Chen,

Hui Chen

School of Automation, Southeast University, 2 Sipailou, Nanjing 210096, China seu.edu.cn

Search for more papers by this author

Hong He,

Hong He

College of Information, Mechanical, and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China shnu.edu.cn

Search for more papers by this author

First published: 01 November 2012

https://doi.org/10.1155/2012/451927

Citations: 2

Academic Editor: Junjie Wei

Share a link

Email
Wechat
Bluesky

Abstract

It has been found that the response of acupuncture point on the human meridian line exhibits nonlinear dynamic behavior when excitation of electroacupuncture is implemented on another meridian point. This nonlinear phenomenon is in fact a hysteretic phenomenon. In order to explore the characteristic of human meridian and finally find a way to improve the treatment of diseases via electro-acupuncture method, it is necessary to identify the model to describe the corresponding dynamic hysteretic phenomenon of human meridian systems stimulated by electric-acupuncture. In this paper, an identification method using nonlinear autoregressive and moving average model with exogenous input (NARMAX) is proposed to model the dynamic hysteresis in human meridian. As the hysteresis is a nonlinear system with multivalued mapping, the traditional NARMAX model is unavailable to it directly. Thus, an expanded input space is constructed to transform the multi-valued mapping of the hysteresis to a one-to-one mapping. Then, the identification method using NARMAX model on the constructed expanded input space is developed. Finally, the proposed method is applied to hysteresis modeling for human meridian systems.

1. Introduction

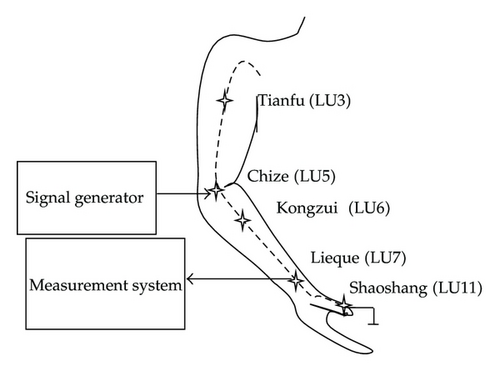
It is known that electro-acupuncture is a modern extension of traditional acupuncture which exists more than three thousand years in Chinese history. Based on the theory of the traditional Chinese medicine, it has been found that the acupuncture points can be grouped in lines called meridian system of the human body. Reference [1] reported that the meridian system has significant effect on human health. References [2, 3] illustrated that the meridian system had architecture with many channels letting electrical signals pass through easily. On the other hand, reference [4] has given a review on electrical properties of acupuncture points and meridians.

Nowadays, most of the research results on electro-acupuncture are focusing on the analysis of impedance on acupuncture points [2, 3, 5–8]. Note that the meridian system is, in fact, a network with several lines or channels. In each channel, there are several acupuncture points located along a line. It was found that there were some relations among those points in each channel. Therefore, the analysis just depending on the impedance of a single acupuncture-point would not reflect the main characteristic of the signal transmission in human meridian system. One of the alternatives is to stimulate an acupuncture-point in a channel with electrical signal and measure the corresponding responses of the other acupuncture points in the same channel simultaneously. Thus the corresponding signal transmission performance of the measured channel can be evaluated. In order to properly evaluate the properties of the meridian channels, construction of an accurate model to describe the behavior of the meridian channel is necessary. Moreover, the obtained models can also be used for understanding and improving the acupuncture therapy, acupuncture doctor training, therapy scheme evaluation, and so forth.

Some research results have illustrated that the human meridian system is a dynamic system [2, 3, 9]. In this case, the identification of the model to describe the dynamic behavior of the meridian is an efficient way for performance evaluation, simulation, and design of optimal stimulation for disease treatment. Reference [9] developed an auto-regressive and moving average model to describe the human meridian system. It fits the response well when the exciting signal with slow frequency and the input amplitude is rather small. However, when the frequency of the exciting input is higher or the amplitude of the exciting signal is larger, it will illustrate some nonlinear behavior especially hysteretic behavior can be found. Thus, a nonlinear dynamic model should be considered to describe this system.

In this paper, the dynamic hysteretic behavior of human meridian system is described. As hysteresis is a nonsmooth nonlinearity with multi-valued mapping, the traditional identification which is used for smooth systems with one-to-one mapping is unavailable directly. In order to transform the multi-valued mapping of hysteresis to a one-to-one mapping, an expanded input space is formed. Then, a nonlinear auto-regressive and moving average model with exogenous input is applied to the identification of the dynamic hysteresis of human meridian. This paper is organized as follows: in Section 2, the hysteretic phenomenon in human meridian is discussed. Then, the expanded input space constructed by input and a modified hysteretic operator is presented in Section 3. Based on the expanded input space, the NARMAX model to describe the hysteresis behavior of human meridian is developed in Section 4. The recursive general identification algorithm (RGIA) is used for parameter estimation of the hysteresis NARMAX model. In Section 5, the convergence of the identification algorithm is discussed. After that, in Section 6, the experimental results of the proposed modeling method is illustrated. Finally, the brief summary is presented in Section 7.

2. Dynamic Hysteresis in Human Meridian

In this section, we will show the corresponding response of the human meridian when the sinusoidal input with sinusoidal signal with different frequencies is applied to the stimulation of meridian system. In this experiment, the Tai-Yin-Lung channel of meridian is chosen for test. The corresponding experimental configuration of meridian signal measurement is shown in Figure 1. The stimulation point is Chize (LU5) while point Shaoshang (LU11) is connected to the ground. The measured meridian point is Lieque (LU7). Figure 2 shows that the hysteretic behavior happened in the response of the measured point Lieque. Note that the corresponding hysteresis behavior varies with different frequencies. It is that the widths of the closed curves are increased as the frequency of input signal increases. Thus, it can be seen that the nonlinearity obviously exists in the response due to the phenomenon of asymmetry and rate-dependence. Moreover, from the experimental results, one can know that the hysteresis in human meridian has the following characteristic, that is,

(1)
performance dependent on the frequency change of input;
(2)
multi-valued mapping of the output against its input; and
(3)
nonsmoothness at the turning points when the input with lower frequency is implemented.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Experimental configuration of meridian signal measurement.

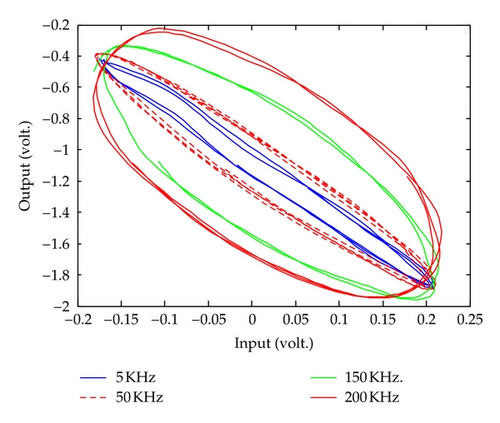
In this situation, the traditional identification methods are rather difficult to be directly used to model the hysteresis existing in human meridian. The existence of hysteresis in human meridian might be explained as tension and spasm caused by external stimulation.

Up till now, there have been some methods proposed for hysteresis modeling, for example, Preisach model [10, 11] and Prandtl-Ishlinskii (PI) model [12]. Those methods used simple backlash operators as the basis functions for modeling. Therefore, lots of operators should be employed in order to obtain accurate models. Although there have been some modified Preisach model [10, 13] as well as modified PI model [14] proposed to describe the hysteresis systems, the structures of those modified schemes are still very complex. In order to simplify the architecture of the model to describe the behavior of hysteresis, references [15] as well as [16] developed the so-called expanded input space based hysteretic models. In the expanded input space, a hysteretic operator which extracted the main movement feature of the hysteresis was introduced as one of the coordinates in the expanded input space. Thus, the multi-valued mapping of hysteresis could be transformed to a one-to-one mapping between the inputs and output. One of the advantages of the expanded input space method is that it can avoid the gradient computation especially at the nonsmooth points of the hysteresis.

3. Expanded Input Space

In this section, a hysteretic operator is developed to extract the main feature of hysteresis and to form a coordinate besides the input coordinate in the expanded input space.

It is well known that hysteresis can be described by the Preisach model. Hence, the hysteresis is continuous and forms a closed loop in the input-output diagram when the input cycles between two extrema.

Then, based on [16], the hysteresis operator f(x) is defined as:

()

where x is the current input, f(x) is the current output, x_p is the dominant extremum adjacent [16] to the current input x. f(x_p) is the output of the operator when the input is x_p.

Therefore, based on the properties of hysteresis operator (referred to [16]), if it is in discrete-time case, Lemmas 3.1 and 3.2 are composed, respectively, that is,

Lemma 3.1. Let x(t) ∈ C(R), and C(R) are the sets of continuous functions on R. If there exist two adjacent time instants t₁ and t₂ (t₁ ≠ t₂), such that x(t₁) = x(t₂), but x(t₁) and x(t₂) are not the local extrema, then f(x(t₁)) ≠ f(x(t₂)).

Lemma 3.2. If there exist two adjacent time instants t₁ and t₂ (t₁ ≠ t₂), such that f(x(t₁)) − f(x(t₂)) → 0, then x(t₁) − x(t₂) → 0.

Remark 3.3. In Lemma 3.1, if x(t₁) = x(t₂), x(t₁) and x(t₂) are not the local extrema, f(x(t₁)) = f(x(t₂)), then in this case, the extreme between t₁ and t₂ does not get sampled in the sampling period. In this situation, the hysteretic operator cannot describe the change tendency of hysteresis. For example, suppose t₁ and t₂ (t₁ < t₂) are two adjacent time instants, in this case, if x(t₁) = x(t₂) and f(x(t₁)) = f(x(t₂)), but the output of hysteresis corresponding to one of the input values is in the increase zone while the output of hysteresis corresponding to another input value is in the decrease zone. In this case, the local extreme between those two output values of the hysteresis is obviously missed in the sampling period. Hence, the hysteretic operator cannot describe the change tendency of hysteresis if this situation happens.

To handle the extremum-missing problem, a modified scheme of the hysteresis operator is proposed in the following theorem.

Theorem 3.4. If x(t₁) = x(t₂), and x(t₁) and x(t₂) are not the local dominant extremes and f(x(t₁)) = f(x(t₂)), where t₁ and t₂ are the adjacent time instants and t₁ < t₂, then, the local dominant extrema located in the segment between points (x(t₁), f(x(t₁))) and (x(t₂), f(x(t₂))) cannot be sampled within the sampling period [t₁, t₂]. In this case, the missed local dominant extreme (x_m(t_m), f(x_m(t_m))) can be estimated by:

()

and the corresponding modified hysteretic operator at estimated local dominant extreme is

()

where Δt = t₂ − t₁, t_m = t₁ + εΔt for maximum estimate and t_m = t₁ − εΔt for minimum estimate.

Proof. As x(t₁) = x(t₂), x(t₁) and x(t₂) are not the local extrema, whilst x(t₁) and x(t₂) are located in the increase and decrease zones, respectively, based on (3.2) and t_m = t₁ + εΔt, it leads to:

()

Then

()

Hence, x_m(t_m) > x(t₁). Moreover, x(t₁) = x(t₂). So, it leads to:

()

Thus, x_m(t_m) = x(t₁) + ε(t_m − t₁), (1 > ε > 0, t_m = t₁ + εΔt) is the local maximum extreme between x(t₁) and x(t₂). Then, the corresponding output of the hysteretic operator is

()

Moreover, we have

()

respectively. It is obvious that f(x(t₁)) ≠ f(x(t₂)), and it satisfies the condition given in Lemma 3.1.

Similarly, if (x_m(t_m), f(x_m(t_m))) is a local dominant minimum point, f(x_m) can be described by

()

Hence, by combining (3.7) and (3.11), the estimated local dominant extreme can be rewritten as

()

Then, we have the following theorem.

Theorem 3.5. If hysteresis can be described by Preisach model, there exists a continuous one-to-one mapping Γ: R₂ → R, such that H[x(t)] = Γ[x(t), f_m(x(t))].

Proof. Firstly, it is proved that Γ is a one-to-one mapping. Let us consider the cases in the following.

Case 1. Assume that x(t) is not the local extremum. In terms of Lemma 3.1, if there exist two different time instants t₁ and t₂, then

()

Therefore, the coordinate (x(t), f_m(x(t))) is uniquely corresponding to hysteresis H[x(t)].

Case 2. Suppose that x(t) is the local extremum. In this case, for two different time instants t₁ and t₂, there will be

()

Case 3. Suppose x(t₁) = x(t₂), f_m(x(t₁)) ≠ f_m(x(t₂)), where t₁ and t₂ are the adjacent time instants and t₁ < t₂, the local extrema located in the segment between points (x(t₁), f_m(x(t₁))) and (x(t₂), f_m(x(t₂))) cannot be obtained within the time period [t₁, t₂]. In this situation, based on Theorem 3.4, we can use (x_m, f_m(x_m)) between those two points to approximate the local dominant extrema.

According to the property of the Preisach-type hysteresis, H[x(t₁)] = H[x(t₂)]. Then the coordinate (x(t), f_m(x(t))) will be uniquely corresponding to hysteresis H[x(t)].

Combining the above-mentioned three situations, it is obtained that Γ is a one-to-one mapping. Next, it will be verified that Γ is a continuous mapping.

According to the property of the Preisach-type hysteresis, if

()

it yields

()

Then, considering Lemma 3.2, if

()

it can be deduced that

()

Then we have H[x(t₁)] − H[x(t₂)] → 0.

Therefore, it can be concluded that there exists a continuous one-to-one mapping Γ: R² → R such that H[x(t)] = Γ (x(t), f_m(x(t))).

Remark 3.6. The theorem stated above shows that the constructed expanded input space consisting of two coordinates, that is, x and f_m(x).

Remark 3.7. Based on Theorem 3.5, the modified hysteretic operator is the combination of (3.2)–(3.4). We can use the modified hysteretic operator to construct an expanded input space.

It has also been proved that the expanded input space is a compact set [16]. Hence, the mapping between the output and the input of the hysteresis on this expanded input space is a one-to-one mapping.

4. Nonlinear ARMAX Model for Hysteresis

Based on the above-mentioned expanded input space, the nonlinear auto-regressive and moving average model with exogenous input (NARMAX) [17] is applied to the identification of dynamic hysteresis in human meridian. In this model, the output of the hysteretic operator in the expanded input space is used as the exogenous input. The corresponding hysteretic model can be described by:

()

where U(t) = [u(t − 1), …, u(t − n_u)] ^T is the input vector, F_m(t − 1) = [f_m(t − 1), …, f_m(t − n_f)] ^T is the exogenous input vector which is, in fact, the output vector of the hysteretic operator,

is the auto-regressive vector, and

is the output of the NARMAX model; g(·) is the dynamic mapping between the input space and the output of the hysteretic model; n_u, n_f, and n_y are the lags for sequences {u}, {f_m}, and

, respectively. For simplification of the representation, (4.1) can also be written as

()

where p is the sum of the maximum lag of the model, {x₁, …, x_n} is the set which consists of the auto-regressive, moving average, and exogenous input items of the model. Hence, the corresponding NARMAX model based on the expanded input space can be described by:

()

where θ = [θ₁, …, θ_n] ^T is the coefficient vector comprised by n = (p + q)!/(p! q!) − 1 coefficients, q is the order of the model. Moreover, in order to simplify the representation of the model, all the variables of the model in the right hand side of the model can be combined into a vector h(t) = [h₁(t), …, h_n(t)] ^T constituted by the product combinations of x₁(t) to x_p(t) from degree 1 to q, that is:

()

Thus, (4.3) can be described as a linear regression expression:

()

For the determination of the model structure, that is, the estimate of the order and lags of the model from the input and output data, the Akaike’s information criterion (AIC) [18] is applied. As the AIC method needs to know the probability distribution of the data which is usually unknown, we replace the likelihood function to the quadratic model error function. Thus, we have:

()

where

and

are the estimate of the coefficient vector θ and the model order, respectively;

represents the quadratic model error function under the condition of

, that is,

()

where e and N are the model error and the data number, respectively. By finding the maximum value of

. Then, we should form a proper combination of n_u, n_f, and n_y via trial and error to the minimize

, and satisfy the constraint n_v + n_f + n_y = p. Finally, the obtained minimized

is used to derive the maximum value of

. Thus, the appropriate

and the proper combination of n_v, n_f, and n_y can be specified.

Then, the corresponding recursive general identification algorithm (RGIA) [19] is applied to the estimation of the parameters of the proposed model. This algorithm is to minimize the quadratic criterion, that is,

()

where the data vector h(k) is replaced by the corresponding

, γ(t) > 0 is a weighted factor, and

; N is the number of data. The online RGIA is as follows:

()

where ρ(k) is the convergent factor, which not only satisfies the conditions given by [20] but also is located within (0, 1), and

()

5. Convergence of the Identification Algorithm

Definition 5.1 (see [20].)Let , θ is the true value vector of the model parameters. Moreover, ξ(t) means that the identification is affected by the estimated errors of the internal variables.

Assumption 5.2. The hysteretic system existing in human meridian is BIBO stable, so y(t) is bounded for any bounded input u(t).

In the following, the convergence analysis on the recursive identification algorithm in the case of absence of noise will be discussed.

Lemma 5.3. Assume input signal u(t) that is bounded but can fully excite the system, then it satisfies , where both α and β are bounded positive real numbers.

Proof. Suppose that input signal u(t) is bounded. Considering Assumption 5.2 leads to the hysteresis system of human meridian is BIBO stable. Thus, the elements of the estimated data vector, that is, are bounded. That implies that there exist two positive real numbers α and β, and they lead to

()

Theorem 5.4. For the algorithm described by (4.9)–(4.15), which is applied to the parameter estimation of the hysteretic model represented by (4.1)–(4.5), if it matches the following conditions, that is,

(1)
the condition of Lemma 5.3 is held;
(2)
P(k) is a positive definite matrix; moreover,
(3)

()

()

()

then the estimated parameter vector

will converge to the true value of the parameter vector θ, as k → ∞, where λ_max[P(k)] and λ_min[P(k)] are the maximum and minimum eigenvalues of P(k), respectively. In (5.4), Δ₁(k) is equal to

()

The proof of this theorem is given in Appendix.

6. Experimental Results

The proposed identification method is applied to modelling of hysteresis inherent in human meridian systems. In this experiment, the sinusoidal signal with attenuating amplitude shown in (6.1) is used to stimulate the meridian point Kongzui on the Taiyin-lung channel but measured the response of another meridian point Chize in the same channel:

()

while the input signal

()

is implemented to excite the same point and obtain the data for model validation test.

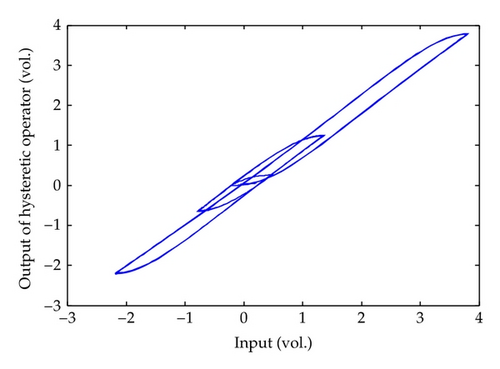
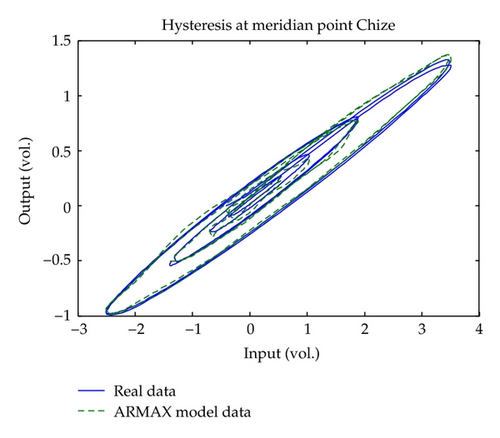
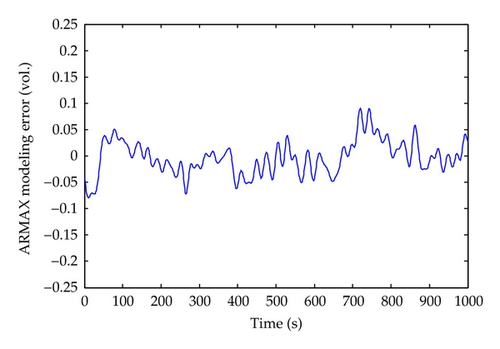
The corresponding input-output plot of the obtained hysteretic operator mentioned in Section 3 is shown in Figure 3, and the hysteresis operator can be used to extract the tendency of hysteresis. Then, the corresponding hysteresis NARMAX model is used to describe the human meridian channel. Moreover, based on the derived input and output data, the model structure is determined by the AIC criterion represented by (4.6) and (4.7). In the experiment, the order-selection procedure is demonstrated in Table 1. It shows that the best result is achieved when n_u = 1, n_f = 1, and n_y = 0, respectively. By randomly setting the initial values of the coefficient vector within [0,1] and λ = 10⁶ of the covariance matrix for the RGIA shown in (4.17), the derived NARMAX model validation result for hysteresis in human meridian is shown in Figure 4 while Figure 5 illustrates the corresponding modelling error of the NARMAX hysteretic model.

Table 1. Model order selection.

Model order	Value of loss function
n_y = 2, n_u = 2, n_f = 2	0.00035181
n_y = 2, n_u = 1, n_f = 2	9.1954e − 006
n_y = 1, n_u = 1, n_f = 2	9.1853e − 006
n_y = 1, n_u = 1, n_f = 1	2.5496e − 005
n_y = 2, n_u = 1, n_f = 1	8.9733e − 006
n_y = 1, n_u = 2, n_f = 1	8.846e − 006
n_y = 0, n_u = 1, n_f = 1	8.6718e − 006

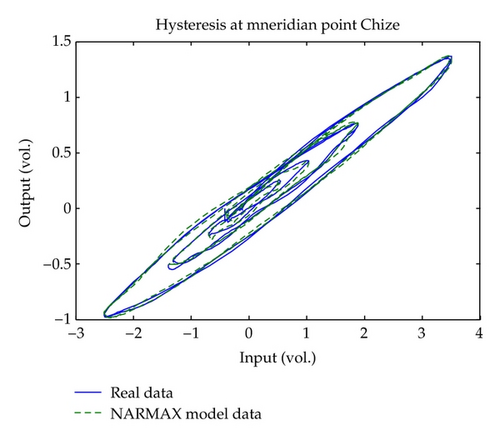
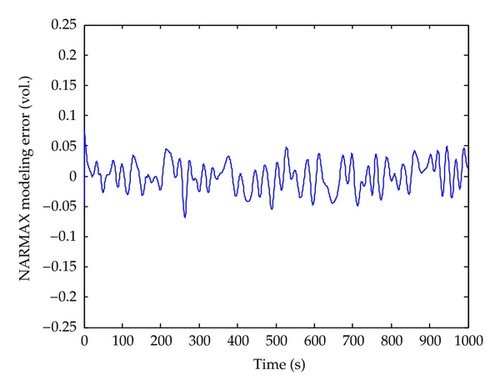
For comparison, the ARMAX model on the expanded input space is also used to identify the hysteresis inherent in human meridian. The model structure is chosen as n_y = 0, n_u = 2, and n_f = 2, respectively. The recursive least squares (RLS) algorithm is implemented for parameter estimate. Figures 6 and 7 illustrate the model validation result and the modeling error of the ARMAX model, respectively. From the comparison, it is seen that the NARMAX model has achieved better modeling result than that of the ARMAX method.

7. Conclusion

In this paper, a nonlinear auto-regressive and moving average model with exogenous input is applied to modeling the hysteretic behavior of human meridian systems. As hysteresis is a nonsmooth nonlinearity with multi-valued mapping, the traditional identification method which is used for smooth systems with one-to-one mapping is unavailable to this case directly. In order to transform the multi-valued mapping of hysteresis to a one-to-one mapping, an expanded input space is formed. Then, a nonlinear auto-regressive and moving average model with exogenous input is applied to the identification of the dynamic hysteresis of human meridian. After that, the RGIA method is used for parameter estimate of the model. The experimental results show that the proposed method is better than the ARMAX modeling method. It provides us with a way to identify the model of the meridian channel in human body so as to construct the potential digital human meridian system for doctor training, evaluation of disease treatment scheme, and human meridian simulations.

Acknowledgment

This work is partially supported by the Leading Academic Discipline Project of Shanghai Normal University (Grant nos. DZL811 and DRL904), the Innovation Program of Shanghai Municipal Education Commission (Grant nos. 11YZ92 and 13YZ056), the National Science Foundation of China (NSFC Grant nos. 61203108, 60971004, and 61171088), the Natural Science Foundation of Shanghai (Grant no. 09ZR1423400), and the Science and Technology Commission of Shanghai Municipality (Grants nos. 09220503000 and 10JC1412200).

Appendix

Proof. From (4.9)–(4.15), it leads to

()

It is known that P⁻¹(k) is a positive definite matrix. Hence, a corresponding quadratic function can be defined as

()

where

, θ is the true value of the parameter vector of the model. Subtracting θ into both sides of (4.10) yields

()

Then, substituting (A.4) into (A.3) derives

()

Equation (A.5) can also be rewritten as

()

Furthermore, substituting (4.12), (A.1), and (A.2) into (A.6) results in

()

Consider forgetting factor μ(k)∈(0, 1] and P⁻¹(k) is a positive definite matrix. Also, it is assumed that ξ(k) satisfies (5.4). Thus, it leads to

()

Hence, it leads to:

()

Based on conditions (5.2) and (5.3) of the theorem, it will yield:

()

Based on (A.9) and (A.10), when k → ∞, we obtain

, that is,

()

References

1 Tsuei J. J., Modern interpretation of acupuncture and the meridian system, Proceedings of the 2nd International Conference on Bioelectromagnetism, February 1998, 177–182, 2-s2.0-0031654209.
Google Scholar
2 Yang H. Y., The research and application of the dynamic testing system for point skin resistance, Journal of Biomedical Engineering. (1997) 16, no. 1, 41–50.
Google Scholar
3 Zhang W., Xu R., and Zhu Z., The influence of acupuncture on the impedance measured by four electrodes on meridians, Acupuncture and Electro-Therapeutics Research. (1999) 24, no. 3-4, 181–188, 2-s2.0-0033495572.
10.3727/036012999816356273
CAS PubMed Web of Science® Google Scholar
4 Ahn A. C., Colbert A. P., Anderson B. J., Martinsen Ø. G., Hammerschlag R., Cina S., Wayne P. M., and Langevin H. M., Electrical properties of acupuncture points and meridians: a systematic review, Bioelectromagnetics. (2008) 29, no. 4, 245–256, 2-s2.0-42949084619, https://doi.org/10.1002/bem.20403.
10.1002/bem.20403
PubMed Web of Science® Google Scholar
5 Becker R., Reichmanis M., Marino A., and Spadaro J., Electrophysiological correlates of acupuncture points and meridians., Psychoenergetic Systems. (1976) 1, 105–112.
Google Scholar
6 Marino R. M. and Ro B., Electrical Correlatesof Acupuncture Points, IEEE Transactions on Biomedical Engineering. (1975) 22, 533–535, https://doi.org/10.1109/TBME.1975.324477.
10.1109/TBME.1975.324477
PubMed Web of Science® Google Scholar
7 Voll R., Twenty years of electroacupuncture diagnosis in Germany. A progress report, American Journal of Acupuncture. (1975) 3, no. 1, 7–17, 2-s2.0-0016768209.
Google Scholar
8 Yamamoto Y. and Yamamoto T., Dynamic System for the Measurement of Electrical Skin Impedance, Medical Progress Through Technology. (1987) 12, 171–183.
10.1007/978-94-009-3361-3_15
CAS PubMed Google Scholar
9 Wang Z., Tan Y., and Su M., Modeling of meridian channels, Proceedings of the 2nd International Conference on Biomedical Electronics and Devices (BIODEVICES ′09), January 2009, 167–172, 2-s2.0-67650694532.
Google Scholar
10 Hu H. and Ben Mrad R., On the classical Preisach model for hysteresis in piezoceramic actuators, Mechatronics. (2003) 13, no. 2, 85–94, 2-s2.0-0037332696, https://doi.org/10.1016/S0957%2D4158(01)00043%2D5.
10.1016/S0957-4158(01)00043-5
Web of Science® Google Scholar
11 Włodarski Z., Alternative preisach models, Physica B. (2005) 367, no. 1–4, 237–242, 2-s2.0-28844486989, https://doi.org/10.1016/j.physb.2005.06.024.
10.1016/j.physb.2005.06.024
CAS Web of Science® Google Scholar
12 Macki J. W., Nistri P., and Zecca P., Mathematical models for hysteresis, SIAM Review A. (1993) 35, no. 1, 94–123, https://doi.org/10.1137/1035005, 1207799, ZBL0771.34018.
10.1137/1035005
Web of Science® Google Scholar
13 Ge P. and Jouaneh M., Modeling hysteresis in piezoceramic actuators, Precision Engineering. (1995) 17, no. 3, 211–221, 2-s2.0-0029342693.
10.1016/0141-6359(95)00002-U
Web of Science® Google Scholar
14 Dong R. and Tan Y., A modified Prandtl-Ishlinskii modeling method for hysteresis, Physica B. (2009) 404, no. 8–11, 1336–1342, 2-s2.0-64549149727, https://doi.org/10.1016/j.physb.2008.12.024.
10.1016/j.physb.2008.12.024
CAS Web of Science® Google Scholar
15 Li C. and Tan Y., A neural networks model for hysteresis nonlinearity, Sensors and Actuators A. (2004) 112, 49–54, https://doi.org/10.1016/j.sna.2003.11.016.
10.1016/j.sna.2003.11.016
CAS Web of Science® Google Scholar
16 Zhao X. and Tan Y., Neural network based identification of Preisach-type hysteresis in piezoelectric actuator using hysteretic operator, Sensors and Actuators A. (2006) 126, no. 2, 306–311, 2-s2.0-31544432002, https://doi.org/10.1016/j.sna.2005.10.023.
10.1016/j.sna.2005.10.023
CAS Web of Science® Google Scholar
17 Chen S. and Billings S. A., Representations of nonlinear systems: the NARMAX model, International Journal of Control. (1989) 49, no. 3, 1013–1032, https://doi.org/10.1080/00207178908547379, 990327, ZBL0674.93009.
10.1080/00207178908559683
Web of Science® Google Scholar
18 Akaike H., A new look at the statistical model identification, IEEE Transactions on Automatic Control. (1974) AC-19, 716–723, 0423716, ZBL0314.62039.
10.1109/TAC.1974.1100705
CAS Web of Science® Google Scholar
19 Dong R., Tan Y., and Chen H., Recursive identification for dynamic systems with backlash, Asian Journal of Control. (2010) 12, no. 1, 26–38, https://doi.org/10.1002/asjc.157, 2676768.
10.1002/asjc.157
PubMed Web of Science® Google Scholar
20 Boutayeb M. and Darouach M., Recursive identification method for MISO Wiener-Hammerstein model, IEEE Transactions on Automatic Control. (1995) 40, no. 2, 287–291, https://doi.org/10.1109/9.341794, 1312896, ZBL0819.93024.
10.1109/9.341794
Web of Science® Google Scholar

Citing Literature

All articles

Identification of Hysteresis in Human Meridian Systems Based on NARMAX Model

Abstract

1. Introduction

2. Dynamic Hysteresis in Human Meridian

3. Expanded Input Space

4. Nonlinear ARMAX Model for Hysteresis

5. Convergence of the Identification Algorithm

6. Experimental Results

7. Conclusion

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Identification of Hysteresis in Human Meridian Systems Based on NARMAX Model

Abstract

1. Introduction

2. Dynamic Hysteresis in Human Meridian

3. Expanded Input Space

4. Nonlinear ARMAX Model for Hysteresis

5. Convergence of the Identification Algorithm

6. Experimental Results

7. Conclusion

Acknowledgment

Appendix

References

Citing Literature

Figures

References

Related

Information