The purpose of this paper is to propose a new kind of P systems on simplicial complexes. We present the basic discrete Morse structure, membrane structures on complexes, and communication rules. A new grid-based clustering technique is described based on this kind of new P systems. Examples are given to show the effect of the algorithm. The new P systems provide an alternative for traditional membrane computing.

1. Introduction

Membrane computing is a new branch of natural computing which is initiated by Păun et al. at the end of 1998, as an attempt to formulate models from the functioning of living cells [1], just like DNA computing coming from genes [2–4]. The advantage of these methods lies in its huge inherent parallelism which has drawn great attention from the scientific community so far. In recent years, many different models of P systems have been proposed, such as cell-like P systems, tissue-like P systems, and spiking neural P systems [5–9]. The obtained computing systems prove to be so powerful that they are equivalent with Turing machines [10] even when using restricted combinations of features and also computationally efficient. Up to now a number of applications were reported in several areas such as biology, biomedicine, linguistics, computer graphics, economics, approximate optimization, cryptography, and so forth.

Traditionally, Morse theory is the subject of differential topology and differential geometry where the topological spaces in question are smooth manifolds. When we want to study discrete problems, we will use combinatorial complexes rather than manifolds. Along this line, discrete Morse theory has been developed [11, 12]. Recently, discrete Morse theory has attracted many researchers because it has found applications in triangulations and graphics. In fact, simplicial complex, the basic data structure in discrete Morse theory, will prove to be an important data structure besides trees and graphs.

Spatial cluster analysis is a traditional problem in knowledge discovery from databases [13]. It has wide applications since increasingly large amounts of data obtained from satellite images, X-ray crystallography, or other automatic equipment are stored in spatial databases. The most classical spatial clustering technique is due to Han and Kamber [13] who developed a variant PAM algorithm called CLARANS, while new techniques are proposed continuously in the literature aiming to reduce the time complexity or to fit for more complicated cluster shapes. Other clustering-like problems include impulsive cluster anticonsensus of discrete multiagent linear dynamic systems [14] and driving general complex networks into prescribed cluster synchronization patterns by using pinning control [15]. In another research, the authors introduce a cooperative article bee colony algorithm for solving clustering problems [16]. Also the authors propose a DNA-based clustering method by the Adleman-Lipton model [17]. For related research, one can also refer to [18–20].

In medical analysis there often appear data clustering problems of various type. The Wisconsin Breast Cancer Showhouse was founded in 1998 as an all-volunteer 501(c)(3) charitable organization by Nance Kinney, a breast cancer survivor (http://www.breastcancershowhouse.org/wbcs2012/index.html). Its mission is to support breast cancer and prostate cancer research at the Medical College of Wisconsin. This breast cancer databases were obtained from the University of Wisconsin Hospitals, Madison from Dr. William H. Wolberg. Many computing methods have been applied to study this data case and, in fact, the Wisconsin Breast Cancer data set is becoming an important testing benchmark for soft computing.

Inspired by the above research, this paper focuses on the joint study of discrete Morse theory with membrane computing. Our purpose is to propose a P system on simplicial complex. Up to our knowledge, this is the first paper to extend membrane computing to complexes. Then we use membrane computing in cluster analysis, providing a new approach to data mining. We first propose a discrete Morse structure for a candidate of a class of new P systems. Then we described for the first time a communication P system on simplices. Then we propose a new method for cluster analysis by simplicial P systems. Finally, we present the Wisconsin Breast Cancer analysis.

2. Discrete Morse Structure

In this section we present some general discrete models which will form the basis of membrane structures. The main idea comes from [11, 21]. In order to do this, we need to present some basic topological concepts. For simplicity we always assume that we are working in an Euclidean space Rⁿ.

2.1. Simplex without Orientation

A k-simplex (cell) σ is the convex hull of k + 1 affinely independent points. More precisely, suppose a₀, a₁, …, a_k are affinely independent, that is, a₁ − a₀, …, a_k − a₀ are linearly independent. Then σ is defined as the set of points in the form , where and λ₀, λ₁, …, λ_k ≥ 0. We will call k the dimension of a simplex and write dim (σ) = k, while a₀, a₁, …, a_k are called vertices of the simplex. A simplex is uniquely indicated by its vertices and hence is expressed as σ = [a₀, a₁, …, a_k], or simply σ = a₀a₁ ⋯ a_k, and will be called a cell in this paper.

A face τ of a simplex σ is defined as a simplex generated by a nonempty subset of its vertices. We write τ < σ. A face τ is called a hyperface of σ if dim τ = dim σ − 1 and is denoted by τ≺σ. In this case, σ is called the parent of τ. Two cells τ₁ and τ₂ are called incident if τ₁, τ₂≺σ, and σ is called the coface of τ₁ and τ₂. Two cells σ₁, σ₂ are called neighbors if they share a common hyperface. The cone from a vertex x to a k-simplex σ is the convex hull of x and σ which yields a (k + 1)-simplex xσ provided x is not an affine combination of the vertices of σ. A simplicial complex K is a finite collection of nonempty simplices for which σ ∈ K and τ≺σ implies τ ∈ K and σ₁, σ₂ ∈ K implies that σ₁∩σ₂ is either empty or a face of both. The underlying space of K is the union of simplices: |K | = ⋃_σ∈Kσ. K_p is a subset of K containing simplices of dimension p.

For a k-simplex σ, define K to be the collection of σ and all its faces. Then it is clear that K is a simplicial complex. We will call this simplicial complex a simple complex or, simply, a complex.

Now we consider some properties of incident and neighborhood relations as described above. First suppose τ₁, τ₂≺σ are incident and dim σ ≥ 2. Then τ₁, τ₂, σ are faces of a simplex. Define ψ = τ₁∩τ₂ and we will show that ψ ≠ ∅. This is evident because if , then p ≥ 2. By removing one vertex we obtain τ₁ and τ₂ with p vertices remained. Since p ≥ 2 we know that there exists at least one common vertex among τ₁, τ₂. By the definition of K we get ψ ∈ K and consequently τ₁, τ₂ are neighbors.

Conversely, if τ₁, τ₂≻ψ are neighbors, they need not be incident as shown in Figure 1. In the case when they are in the same simplex, however, this is true. In fact, suppose . Then all the vertices belong to τ₁ and τ₂. Then we can assume that and . Since both cells are in the same simplex, define . Then σ ∈ K. Consequently τ₁, τ₂ are incident. Putting everything together we get a theorem.

Details are in the caption following the image — **Figure 1 (a) incident relation**
Open in figure viewer PowerPoint

An attractor model on simplicial complex.

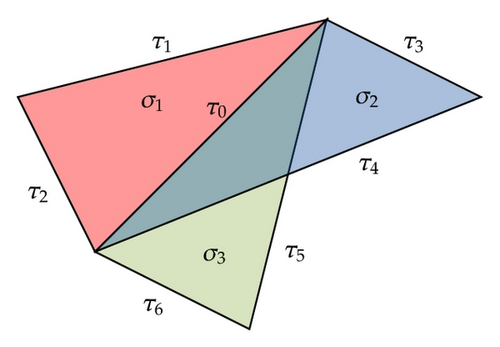
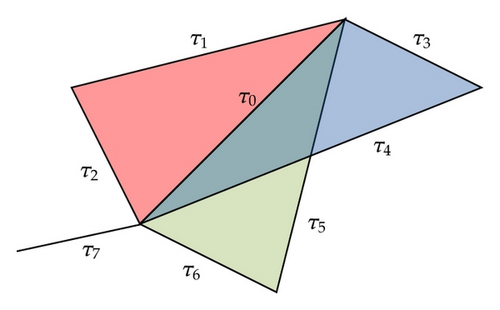
Theorem 2.1. Two incident cells τ₁, τ₂ are neighbors if they are at least one-dimensional. Two neighboring cells are incident provided they are located in the same simplex.

By the definition of neighborhood, if σ₁, σ₂ are neighbors and their common hyperface is τ, then clearly τ = σ₁∩σ₂ and, consequently, this common hyperface is unique. However, there exist cells with nonempty intersection but they are not neighbors. Now we consider incident cells τ₁, τ₂≺σ. We will show that their coface is also unique. First if dim τ₁ = dim τ₂ = 0, then dim σ = 1. Therefore σ is the edge joining the two vertices τ₁, τ₂ and hence is unique. Next if dim τ₁ = dim τ₂ ≥ 1, then as described previously we define ψ = τ₁∩τ₂. Then τ₁ = v₁ψ, τ₂ = v₂ψ and v₁ ≠ v₂. Therefore σ = v₁v₂ψ and is unique.

Theorem 2.2. Neighboring cells can only share a unique common hyperface. Incident cells have a unique coface (parent).

2.2. Simplex with Orientation

Simplicial complexes with orientation are important tools in the study of topological properties of discrete data structure. Concepts about discrete Morse functions are listed as follows (Robin [11]). For a simplex σ = [a₀, a₁, …, a_k], there are two orientations and the opposite orientation is denoted by −σ. Figure 2 shows the orientation of a three-dimensional complex.

In the following we will use

to denote a face of σ, where the vertex a_i is eliminated. The following chain is defined as the boundary of the complex:

(2.1)

If g_i are integers, then ∑_ig_iσ_i is called a chain, where dim σ_i remains the same within a chain. Boundary operator extends to chains naturally. An important property of boundary operator is that ∂∘∂ = 0. For a (k − 1)-dimensional simplex τ^k−1 and a k-dimensional simplex σ_k, define its relationship operator as follows:

(2.2)

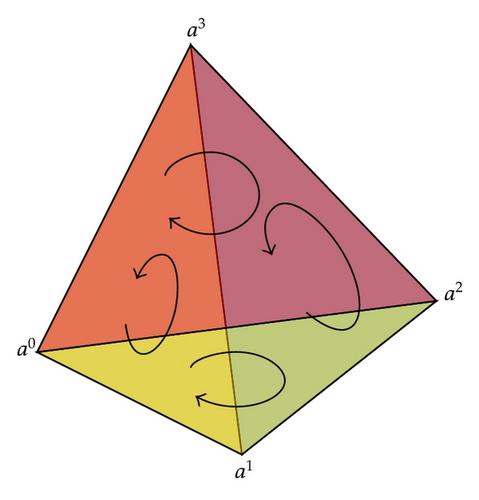
In simplicial complex we can define Morse functions which is a tool for optimization.

Definition 2.3. Let K be a simplicial complex. A function f : K → R is a discrete Morse function if for every σ^p ∈ K_p the following two statements are true:

(1) #{τ^p+1 > σ∣f(τ) ≤ f(σ)} ≤ 1; #{v^p−1 < σ∣f(v) ≥ f(σ)} ≤ 1.

A simplex σ^p is critical with index p if
(2) #{τ^p+1 > σ∣f(τ) ≤ f(σ)} = 0; #{v^p−1 < σ∣f(v) ≥ f(σ)} = 0.

Discrete gradient can also be defined on the complex K. If v is a critical point, then define V(v) = 0. Otherwise if v ∈ K₀ is not critical and the edge e satisfies e > v, f(e) ≤ f(v), then define V(v) = ±e where the sign is determined so that 〈∂(V(v)), v〉 = −1. Here the inner product 〈·, ·〉 is the obvious inner product on oriented chains with respect to which the oriented simplices are orthonormal. It is easy to see that, if the edge e = vu, then V(v) = −e. Generally speaking, discrete gradient is a mapping

(2.3)

A natural gradient flow is Φ(σ) = σ + ∂V(σ) + V(∂σ).

3. Communication P Systems on Simplices

3.1. Traditional P Systems

Membrane is a structure serving as a protected reactor. We will identify a membrane m with its delimited space. When we say inclusion for membranes, it is always strict inclusion. Now we list some elementary concepts concerning the basic operations of membranes:

(i)
m, m^′ are vicinal, if m^′ ⊂ m and there is no m^′′ such that m^′ ⊂ m^′′ ⊂ m,
(ii)
elementary membrane: with no lower vicinal membranes, skin membrane: with no upper vicinal membranes, we assume there is always a unique skin,
(iii)
degree: number of membranes,
(iv)
sibling membranes m, m^′: if there is a m^′′ which is upper vicinal for both m and m^′.

Parentheses expression is often used to describe membrane structures. For example, the membrane structure as shown in Figure 3 has a parentheses expression for membranes as follows:

(3.1)

For a set U, a multiset over U is a mapping M : U → N, where N is the set of nonnegative integers. For a ∈ U, M(a) is the multiplicity of a in M. Suppose the set of objects is O with a subset E such that objects from E are available in the environment in arbitrary multiplicities, that is, its multiset is M : E → {∞}. A P system with symport/antiport rules of degree m ≥ 1 is a construct

(3.2)

where O is the alphabet, T ⊂ O is the alphabet of terminal objects, μ is a membrane structure of degree m, ω₁, …, ω_m are the multisets of objects associated with the m regions of μ, and R₁, …, R_m are finite sets of symport and antiport rules associated with the m membranes of μ, and i₀ is the input/output region.

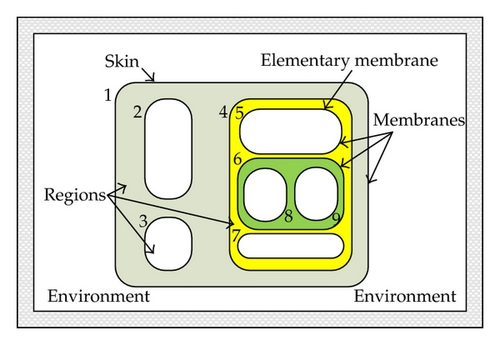
A P system is called stable if, even if some rules are still applicable, their application does not change the string/object content of the membrane structure, nor the membrane structure itself. For a subalphabet W ⊂ O, we call a system stable over W if the projection over W of the string/object remains unchanged, even if some rules are still applicable. If W = {a}, we will say stable over a. If , with for 1 ≤ i ≤ m, is a subset of rules, we call a P system stable with respect to the rules R^′ if the P system with rules R′ is stable (i.e., applications of rules in R′ do not change the string/object content of the system’s membranes) [19].

3.2. Membrane Structures on Simplices

Now we describe membrane structures on simplicial complexes. First we assume that the complex is a simple complex, that is, a simplex with all its faces including vertices. In Figure 4 a simple three dimensional example is presented with 15 membranes. In the general case when there is a complex {a⁰, a¹, …, aⁿ} in Rⁿ, the number of simplices are

(3.3)

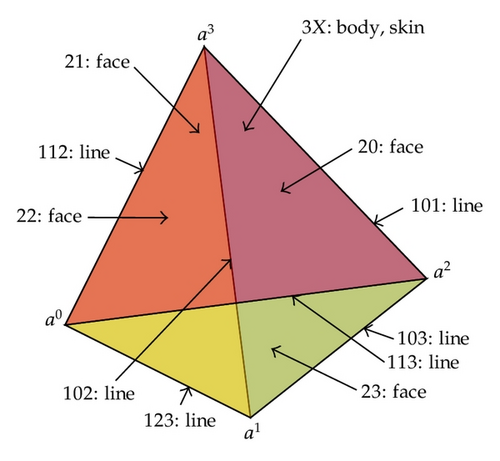
The boundary relations of simplices are shown in Figure 5 where the arrows point to the boundary cells.

Now we consider the general cases where K is a simplicial complex in Rⁿ. For an example of K in R³ as shown in Figure 6, the total number of cells is 6 + 19 + 21 + 9 = 55. For example, the three dimensional simplices are listed as

(3.4)

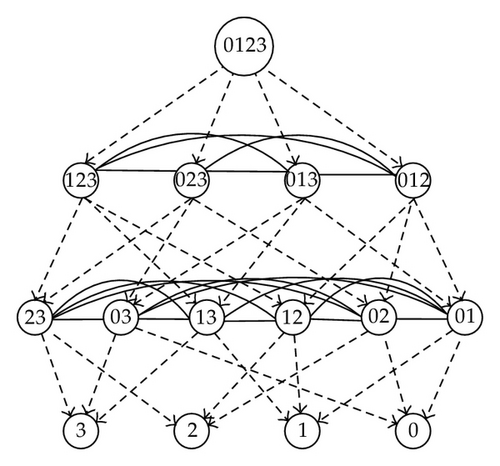
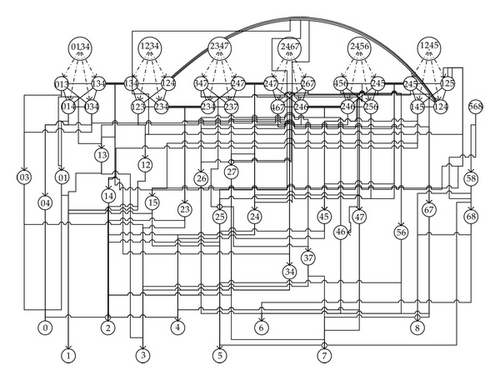
Generally speaking, a simplicial complex K is denoted by a set of vertices {a⁰, a¹, …, a^k} in Rⁿ. A simplex σ ∈ K is called membrane. A membrane is called a max-simplex if it is not a face of another simplex in K. A simplex is denoted by its vertices. Evidently, vertices are zero-dimensional cells and hence are elementary membranes. If τ≺σ is a face of σ, then we way that σ is the parent of τ. Figure 5 shows the parents and neighborhood relations of the complex in Figure 4. For the more general simplicial complex as in Figure 6, the network model is shown in Figure 7.

If σ₁, σ₂ are incident, we say there is an upper link (channel) between σ₁, σ₂. If σ₁, σ₂ are neighbors, we say there is a lower link between them. A upper link is denoted by (σ₁, σ₂) ^τ, where τ is their (common) parent, while lower link is written as (σ₁, σ₂) _τ, where τ is their common hyperface. Upper link is also written by (σ₁, σ₂) _U or, simply, (σ₁, σ₂), while lower link is denoted by (σ₁, σ₂) _L. Links have no directions. Thus (σ₁, σ₂) and (σ₂, σ₁) are identical. We will specify one from these two links, and only one is allowed.

Definition 3.1. A P system on a simplicial complex K, called a simplicial P system, with antiport and symport rules is a construct

(3.5)

where m is the number of cells labeled with 1,2, …, m, O is the alphabet, E is the set of objects with unlimited multiplicity in the environment, ω₁, …, ω_m are initial strings over O of multiset, R₁, …, R_m are symport and antiport rules associated with the m membranes, ch⊆{(i, j) _R, (i, j) _L : i, j ∈ {1, …, m}} is the set of links, and F(i, j) is a finite set of antiport and/or symport rules associated with the link (i, j) ∈ ch.

Ceterchi and Martin-Vide [19] proposed a new type of communication P systems with priority relations. They introduced a promoter for a rule to be active and a inhibitor for it to be inactive. Induced by their idea, we will present an ordered system in this section.

An antiport rule (u, out; v, in) _i in R_i exchanges the multiset u inside R_i with v outside it. A symport rule (x, out) _i (or (x, in) _i) sends out (takes in) the multiset x with respect to membrane R_i. For a specific membrane R_i, rules are totally ordered as r₁ > r₂ > ⋯>r_n > r_n+1 > ⋯. The rule r_n+1 is applicable if and only if the system has reached a stable configuration with respect to rules r₁ > ⋯>r_n. We can use a queue structure to represent this process.

3.3. Rules in Simplicial P Systems

Now we describe the communication rules in simplicial P systems. For our purpose in this paper, there are mainly four types of communication rules in a simplicial P system. Each type of rule may have operators such as out, in, up, down.

First suppose (τ₁, τ₂) _σ is an upper link. A rule like [(x, y), up] ^U means that the multiset x and y from τ₁ and τ₂ transform into z and go up to their parent σ. For two cells τ≺σ, the antiport rule [u, out; v, in∣τ≺σ] in τ means exchanging multiset u inside membrane τ with the multiset v outside it (in σ). The symport rule [u, out∣τ≺σ] sends the multiset u outside τ. Another symport rule [u, in∣τ≺σ] works similarly.

An upper link rule in R^σ(τ₁, τ₂) may have the following forms:

(3.6)

(3.7)

An lower link rule in R_σ(τ₁, τ₂) may have the following forms:

(3.8)

(3.9)

Equation (3.6) means moving x from cell τ₁ and y from τ₂ to z to parent σ and simultaneously moving γ from σ to α into τ₁ and β into τ₂. Equation (3.8) means moving x from cell τ₁ and y from τ₂ to z to hyperface σ and simultaneously moving γ from σ to α up to τ₁ and β up to τ₂.

3.4. Configuration and Computation

Now we describe the configuration and computation of simplicial P systems. For our purpose, change of membrane structure is not involved. A configuration of a simplicial P system is the state of the system described by specifying the objects and rules associated to each membrane. The initial state is called initial configuration. Therefore, the multisets represented by ω_i, 1 ≤ i ≤ d in Π, constitute the initial configuration of the system.

The system evolves by applying rules in membranes and this evolution is called computation. The computation starts with the multisets specified by ω₁, …, ω_m in the m cells. In each time unit, rules are used in a cell. If no rule is applicable for a cell, then no object changes in it. The system is synchronously evolving for all cells.

When the system has reached a configuration in which no rule is any longer applicable, we say that the computation halts. A configuration is stable if, even if some rules are still applicable, their application does not change the object content of the membranes. The computation is successful if and only if it halts, or it is stable. The result of a halting/stable computation is the number described by the multiplicity of objects present in the cell i₀ in the halting/stable configuration.

4. Cluster Analysis by Simplicial P Systems

4.1. Problem Setting and Algorithm

Now suppose the data set to be clustered is

. We now construct a uniform grid in Rⁿ as follows. Choose integers n_i > 0 and let δ_i = (Q_i − P_i)/n_i, and divide the interval [P_i, Q_i] into n_i subintervals [P_i, P_i + δ_i), …, [Q_i − δ_i, Q_i). Therefore X is contained in the following grid 𝒢 with N = n₁ · n₂ ⋯ n_n − N₀ cells, where N₀ is the number of cells that do not contain data:

(4.1)

Then we can define a new data set Ω = {x₁, …, x_N}, where x_i is each grid point

(4.2)

Define a weight function on Ω by m(x) = #{z_i∈ the cell corresponding to the data x}. In this way, the original data set is transformed into a new data set Ω with weights equal to the original number of points. Next we will always work on the data set Ω. For simplicity, we will consider a density-based clustering technique. For two points x, y ∈ Ω, the similarity is defined by

(4.3)

where d(x, y) is the topological distance of the two points. That is, if x, y are incident, then d(x, y) = 1. Else d(x, y) is the minimal number of edges which form a path connecting x and y. For two subsets C₁, C₂ ⊂ X, the similarity is defined by

(4.4)

The clustering is implemented by a hierarchical method as follows. At first, each point of the data set X forms a cluster which contains a singleton. Then each data point tries to connect another data point in its neighborhood. After this step, a cluster can be found as connected points. Now we construct a simplicial complex K corresponding to the data set Ω. On the basis of the rectangles as in (4.1), we add some hyperplanes to form a triangulation. Then each rectangle is decomposed as several simplices. Hyperplanes can be chosen such that the set of simplices satisfy the definition of simplicial complex. And then K is defined as the union of such simplices. In the three dimensional case, this is shown as in Figure 8.

Now we will show that the triangulation as above exists. In fact, we need only to consider an inner cell

, where r_i < p_i < q_i < s_i. There are 2ⁿ vertices for this cell

(4.5)

There are totally 3ⁿ − 1 surrounding cells

(4.6)

First we consider the triangulation of the cell C. Now we choose one vertex v₀ = [z₁, …, z_n] from the cell C where z_i can be p_i or q_i. Now we denote

(4.7)

Consider the vertex set

(4.8)

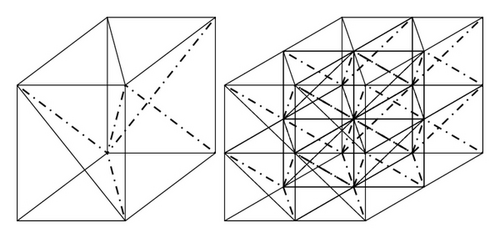
Then #(S_j) = 2ⁿ⁻¹. Clearly C can be decomposed as disjoint cones . Notice that S_j is an (n − 1)-dimensional rectangle and this means that, for any triangulation of S_j, we can join them with v₀ to form a triangulation of v₀C. Therefore by induction we get the construction of triangulation.

Lemma 4.1. The decomposition is valid with the property that each pair of Int(v₀S_j) is disjoint, where Int(C) is the set of interior points in Rⁿ.

Proof. Suppose x = [a₁, …, a_n] ∈ C and x ≠ v₀. Consider the point x_t = (1 − t)v₀ + tx = [(1 − t)z₁+ta₁, …, (1 − t)z_n + ta_n] where t ≥ 1. Let t₀ be the first zero point of the following function:

(4.9)

Clearly ϕ(1) ≥ 0. Let . Then x ∈ v₀S_J.

By the above discussion, we also have another lemma.

Lemma 4.2. Suppose the triangulation of S_j in Rⁿ⁻¹ is . Then the set forms a triangulation of C.

Finally we obtain a theorem.

Theorem 4.3. A simplicial complex K exists corresponding to the grids 𝒢.

For each node x ∈ Ω, define its neighborhood as 𝒩(x) = {y ∈ Ω∣y is incident with x in K}. For a subset C ⊂ Ω, define its neighborhood 𝒩(C) as 𝒩(C) = ⋃_x∈C𝒩(x).

Now we propose an algorithm for our clustering problem. This is a self-joining cluster technique. Initially, one data point in Ω forms a cluster of singleton. Then each node searches for its neighborhood. If there exists a neighboring node which is similar enough, then activate a link between the two nodes. The final cluster is linked nodes. To define the meaning of similar enough, we need a parameter δ₀ such that f(x, y) > δ₀. Putting everything together, we get the algorithm as shown in Algorithm 1.

Algorithm 1: A self-joining clustering algorithm.

Inputs: Ω = {x₁, x₂, …, x_N}, δ₀: similarity threshold value, 𝒩_i = {y∣y, x_i are incident}
Outputs: 𝒞 = {C₁, C₂, …, C_t}: set of clusters, t: number of clusters, Ω₀: outliers
Begin
Set Ω₁ = Ω₀ = ∅, C₁ = ∅, t = 1.
for i = 1 to N
If 𝒩_i = ∅, then add x_i into set Ω₀. Otherwise add x_i into set Ω₁. For each x_j ∈ 𝒩_i, j > i, calculate
the similarity measure f(x_i, y). If f(x_i, y) > δ₀, then set the edge σ(x_iy) as active. In this case, set
C₁ = {x_i} if C₁ is still an empty set.
end
while Ω₁ ≠ ∅ do
(1) For each x ∈ Ω₁ if there exists an active edge σ(xy) with x ≠ y, y ∈ C_t, then add x into C_t and
remove x from Ω₁.
(2) t = t + 1.
end
End

4.2. Design of a P System

Now we have already defined the simplicial complex K as the membrane structure with M total membranes. Next we need to specify the alphabet and rules to be used. First we design a binary coding scheme for the weight function m(·)and the distance function d(x, y). Suppose the length of the coding is L. In this way, the weight function and the distance function take binary strings as values. Now we suppose m(x_i) = m_i1 ⋯ m_iL, where m_ij = 0,1. We also need an integer H such that if the coding of δ₀ is d₁d₂ ⋯ d_L, then

(4.10)

Suppose μ ⊂ ch is a subset of links. Then we can define a P system as follows:

(4.11)

The working alphabet is

(4.12)

Let v_i = x_i, i = 1, …, N be the vertices. We will use to denote a k-dimensional simplex. Therefore σ(v_i) is a vertex or v_i for short. Define N_i = #(𝒩_i). ch is the set of edges in K.

The initial multiset ω_i stands for the multiset in the membrane σ(v_i):

(4.13)

For (i, j) ∈ μ, rules are

with the order as follows:

(4.14)

Rules on edges are

(4.15)

5. Example and Discussion

The Wisconsin breast cancer data set consists of 699 samples with 9 attributes. The samples are classified as two categories, the malignant and the benign. The nine attributes are Clump-Thickness, Cell-Size-Uniformity, Cell-Shape-Uniformity, Marginal-Adhesion, Single-Epi-Cell-Size, Bare-Nuclei, Bland-Chromatin, Normal-Nucleoli, and Mitoses. The data is shown in Figure 9 with an added noise of [0,0.5].

Now we choose attributes 2 and 6 and accumulate the data samples and use the grid technique proposed in this paper. Then the data set is shown in the following matrix:

(5.1)

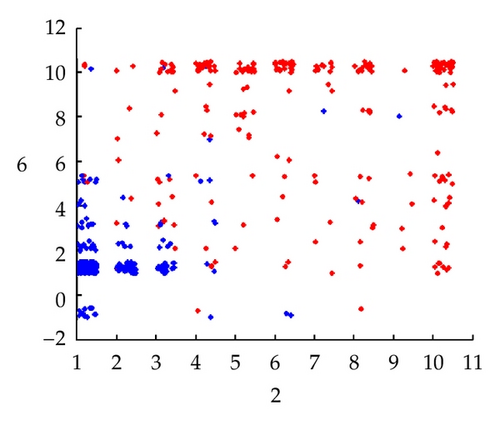
Next we construct a simplicial complex K as shown in Figure 10 in R² where each vertex corresponds to the data points as in (5.1).

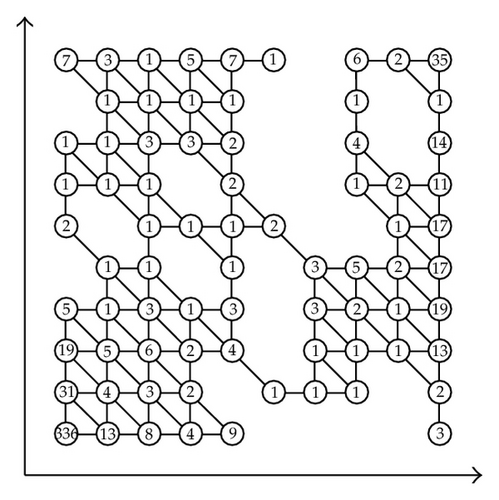
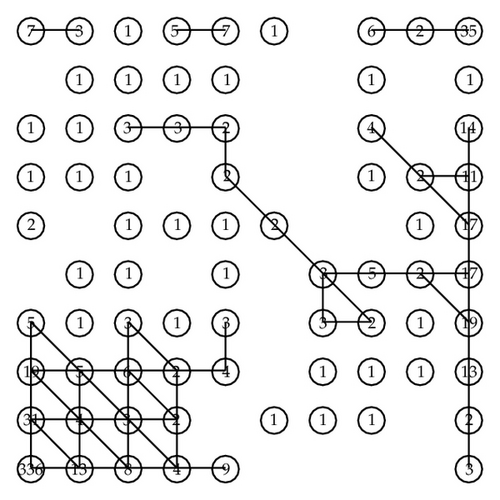
We now define L = 9. Then 2^L = 512 and N = 100 − 25 = 75. Now we choose δ₀ = 1. Then the final cluster is shown in Figure 11. We find five clusters and 31 outliers.

Next we choose attributes 1 and 2 and then the data matrix is

(5.2)

Now we analyze the effect of the parameter δ₀. First we choose δ₀ = 0. Then the clustering result is one cluster with all data. Then the ill clustered points is 699. Next let δ₀ = 1. Then we get two clusters and some outliers. However, in this case the red data are all ill-clustered and hence the error rate is 241. Now choose δ₀ = 2. In this case we find four clusters. The number of outliers are 46 while the ill-clustered points are 65 + 74 = 139. Then the total number is 185. Next choose δ₀ = 3. This time we find 6 clusters. Number of outliers is 87. Number of ill-clustered points is 91. Number of other error points is 40 hence the total number is 218. Again we choose δ₀ = 4. In this time we obtain 4 clusters with a large outlier (outlier number: 157, error clusters: 65, other errors: 13, total number: 235). The error line is shown in Figure 12.

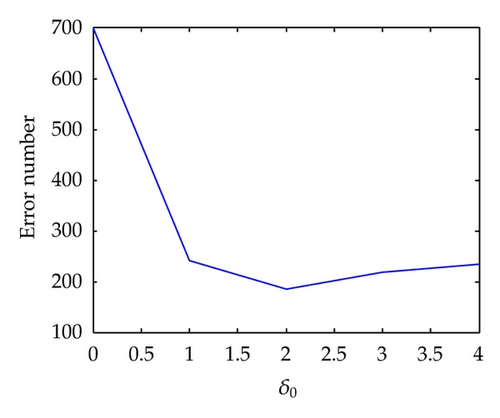
As a result we see that the best parameter is δ₀ = 2.

Acknowledgments

This research is supported by the Natural Science Foundation of China (no. 61170038,71071090,60873058), the Natural Science Foundation of Shandong Province (no. ZR2011FM001), and the Shandong Soft Science Major Project (No. 2010RKMA2005).

References

1 Păun G., Rozenberg G., and Salomaa A., Membrane Computing, 2010, Oxford University Press, New York, NY, USA, https://doi.org/10.1007/978-3-642-11467-0, ZBL1231.83028.
10.1007/978-3-642-11467-0
Google Scholar
2 Adleman L. M., Molecular computation of solutions to combinatorial problems, Science. (1994) 266, no. 5187, 1021–1024, 2-s2.0-0028114541, https://doi.org/10.1126/science.7973651.
10.1126/science.7973651
CAS PubMed Web of Science® Google Scholar
3 Lipton R. J., DNA solution of hard computational problems, Science. (1995) 268, no. 5210, 542–545, 2-s2.0-0029278612, https://doi.org/10.1126/science.7725098.
10.1126/science.7725098
CAS PubMed Web of Science® Google Scholar
4 Păun G., Rozenberg G., and Salomaa A., DNA Computing, New Computing Paradigms, 2010, Springer, Berlin, Germany, 1724525.
Google Scholar
5 Ishdorj T.-O., Leporati A., Pan L., Zeng X., and Zhang X., Deterministic solutions to QSAT and Q3SAT by spiking neural P systems with pre-computed resources, Theoretical Computer Science. (2010) 411, no. 25, 2345–2358, https://doi.org/10.1016/j.tcs.2010.01.019, 2664113, ZBL1208.68172.
10.1016/j.tcs.2010.01.019
Web of Science® Google Scholar
6 Linqiang P. and Alhazov A., Solving HPP and SAT by P systems with active membranes and separation rules, Acta Informatica. (2006) 43, no. 2, 131–145, https://doi.org/10.1007/s00236-006-0018-8, 2248798, ZBL1097.68045.
10.1007/s00236-006-0018-8
Web of Science® Google Scholar
7 Linqiang P. and Mart´ın-Vide C., Solving multidimensional 0-1 knapsack problem by P systems with input and active membranes, Journal of Parallel and Distributed Computing. (2005) 65, no. 12, 1578–1584.
10.1016/j.jpdc.2005.05.018
Web of Science® Google Scholar
8 Ishdorj T.-O, Leporati A., Linqiang P., and Wang J., Solving NP-Complete problems by spiking neural p systems with budding rules, Proceedings of the 10th International Conference on Membrane Computing, 2009, 335–353.
Google Scholar
9 Linqiang P., Zeng X., Zhang X., and Jiang Y., Spiking neural P systems with weighted synapses, Neural Processing Letters. (2012) 35, no. 1, 13–27, https://doi.org/10.1007/s11063-011-9201-1.
10.1007/s11063-011-9201-1
Web of Science® Google Scholar
10 Păun G., A quick introduction to membrane computing, The Journal of Logic and Algebraic Programming. (2010) 79, no. 6, 291–294, https://doi.org/10.1016/j.jlap.2010.04.002, 2682171, ZBL1208.68127.
10.1016/j.jlap.2010.04.002
Google Scholar
11 Robin F., Morse theory for cell complexes, Advances in Mathematics. (1998) 134, no. 1, 90–145, https://doi.org/10.1006/aima.1997.1650, 1612391, ZBL0929.57020.
10.1006/aima.1997.1650
Web of Science® Google Scholar
12 Robin F., Users guide to discrete Morse theory, Séminaire Lotharingien de Combinatoire. (2002) 48, article B48c, 1–35, 1939695, ZBL1048.57015.
Google Scholar
13 Han J. and Kamber M., Data Mining, Concepts and Techniques, 2002, Higher Education Press, Beijing, China, Morgan Kaufmann Publishers.
Google Scholar
14 Zhang L. and Jiang H., Impulsive cluster anticonsensus of discrete multiagent linear dynamic systems, Discrete Dynamics in Nature and Society. (2012) 2012, 11, 857561, https://doi.org/10.1155/2012/857561.
10.1155/2012/857561
Web of Science® Google Scholar
15 Feng J., Wang J., Xu C., and Austin F., Cluster synchronization of nonlinearly coupled complex networks via pinning control, Discrete Dynamics in Nature and Society. (2011) 2011, 23, 262349, https://doi.org/10.1155/2011/262349, 2853349.
10.1155/2011/262349
Web of Science® Google Scholar
16 Zou W., Zhu Y., Chen H., and Sui X., A clustering approach using cooperative artificial bee colony algorithm, Discrete Dynamics in Nature and Society. (2010) 2010, 16, 459796, https://doi.org/10.1155/2010/459796, 2738170, ZBL1201.68112.
10.1155/2010/459796
Web of Science® Google Scholar
17 Liu X., Xiang L., Wang X. et al., Spatial cluster analysis by the adleman-lipton DNA computing model and flexible grids, Discrete Dynamics in Nature and Society. (2012) 2012, 32, 894207, https://doi.org/10.1155/2012/894207.
10.1155/2012/894207
Web of Science® Google Scholar
18 Mónica C., Angels Colomer M., Pérez-Jiménez M. J., and Zaragoza A., Hierarchical clustering with membrane computing, Computing and Informatics. (2008) 27, no. 3+, 497–513, 2477623.
Web of Science® Google Scholar
19 Ceterchi R. and Martin-Vide C., P systems with communication for static sorting, GRLMC Report, 2003, no. 26, Rovira I Virgili University, M. Cavaliere, C. Mart´ın-Vide, and Gh. Paun, eds.
Google Scholar
20 Abu Bakar R. B., Watada J., and Pedrycz W., DNA approach to solve clustering problem based on a mutual order, BioSystems. (2008) 91, 1–12, https://doi.org/10.1016/j.biosystems.2007.06.002.
10.1016/j.biosystems.2007.06.002
PubMed Web of Science® Google Scholar
21 Natarajan V. and Edelsbrunner H., Simplication of three-dimensional density maps, IEEE Transactions on Visualization and Computer Graphics. (2004) 10, 587–597, https://doi.org/10.1109/TVCG.2004.32.
10.1109/TVCG.2004.32
PubMed Web of Science® Google Scholar

Citing Literature

All articles

Communication P Systems on Simplicial Complexes with Applications in Cluster Analysis

Abstract

1. Introduction