Advances in Tribology
Volume 2012, Issue 1 412190
Research Article
Open Access

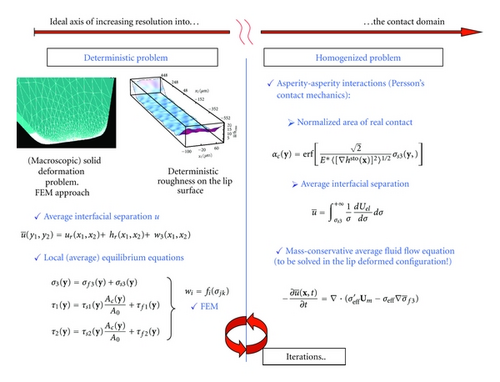
A Two-Scale Approach for Lubricated Soft-Contact Modeling: An Application to Lip-Seal Geometry

Michele Scaraggi, 

Corresponding Author

Michele Scaraggi

DII, Universitá del Salento, 73100 Monteroni di Lecce, Italy unisalento.it

Search for more papers by this author
Giuseppe Carbone, 

Giuseppe Carbone

DMMM, Politecnico di Bari, 70126 Bari, Italy poliba.it

Search for more papers by this author
First published: 19 November 2012
https://doi.org/10.1155/2012/412190
Citations: 10
Academic Editor: Michel Fillon

Abstract

We consider the case of soft contacts in mixed lubrication conditions. We develop a novel, two scales contact algorithm in which the fluid- and asperity-asperity interactions are modeled within a deterministic or statistic scheme depending on the length scale at which those interactions are observed. In particular, the effects of large-scale roughness are deterministically calculated, whereas those of small-scale roughness are included by solving the corresponding homogenized problem. The contact scheme is then applied to the modeling of dynamic seals. The main advantage of the approach is the tunable compromise between the high-computing demanding characteristics of deterministic calculations and the much lower computing requirements of the homogenized solutions.

1. Introduction

Compliant contacts, most commonly known as soft-contacts, are very common in nature (e.g., cartilage lubrication, eye-eyelid contact) and technology (e.g., tires, rubber sealings, adhesives). It has long been stated that the friction and fluid leakage characteristics of wet soft-contacts are strongly related, among the other factors, to the local interactions occurring at the contact interface [1–5]. In the case of randomly rough surfaces, the basic understanding of the role played by the asperity-asperity and fluid-asperity interactions, occurring over a wide range of roughness length-scales, has been largely investigated and debated in the very recent scientific literature [6–12]. Given the (usual) fractal nature of random roughness, a number of interesting phenomena have been highlighted, as for example, the viscous-hydroplaning [6], the viscous flattening [9–15], the fluid-induced roughness anisotropic deformation [10, 11], the local [10, 11] and global [8, 16] fluid entrapment, and many others. The way to deal with random roughness contact mechanics, despite being nontrivial and suffering of a certain description fragmentation, is however well described in the current scientific literature.

On the other side, nowadays bio-inspired research [17, 18], together with the widely-spreading practice of surface engineering [19], is showing the many (mainly unexplored) opportunities offered by the physical-chemical ordered modification of surfaces in order to tailor targeted macroscopic contact characteristics, such as adhesion and friction. Bio-inspired adhesive research [20] is probably the best state of the art example of such research trend. However, investigating the combined effect of, let us say, quantized roughness and fluid action has not equally attracted the scientific community attention, apart from few experimental investigations [12, 21, 22] and basic theoretical investigations [23, 24]. This may be justified by the complexity of the numerical formulation of the problem, which is expected to not to present an analytical treatment. As a result, and to the best of authors’ knowledge, the combined effect of lubricant action and single-scale (contact splitter) roughness has not been practically investigated by tribologists’ community.

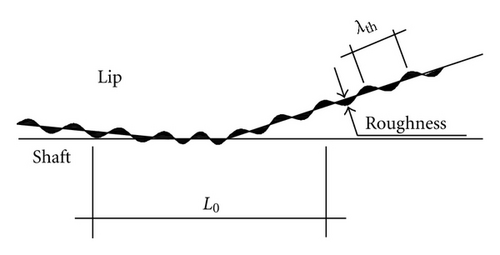
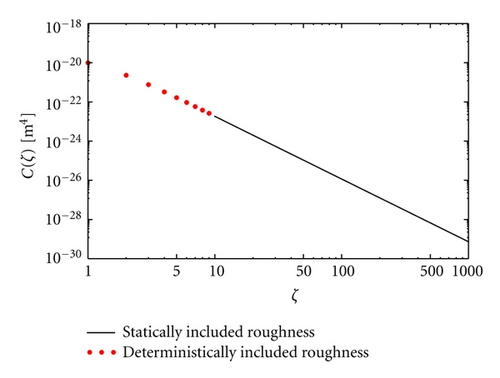
In this work we give our personal contribution to this research field and, in particular, we discuss a novel numerical scheme of soft mixed lubrication, which can be adopted to perform such investigations. In our model the roughness is split into two contributions. A threshold scale ζth = L0/λth > 1 (where L0 is the representative macroscopic size of the contact and λth is the threshold roughness length-scale) is identified. For length scales λ = L0/ζ>λth, that is ζ < ζth, the system is investigated by using a deterministic approach, whereas for λ = L0/ζ ≤ λth, that is, ζ ≥ ζth, the problem is treated by homogenizing the equations. This is of utmost help in performing numerical simulations, as for example in the case of microstructured or bio-inspired surfaces where the surface geometry roughness is characterized by a single scale texture (e.g., a pillars array) combined with random roughness at sub-micrometer scales. The main advantage of the proposed approach is, therefore, the strong reduction of numerical complexity. The paper is organized as follows. In Section 2 we describe the mixed lubrication model scheme (we refer to appendix for the details of numerics), whereas in Section 3 we report an example of application of the proposed model to the case of a lip sealing geometry operating in steady-sliding contact. For a detailed description on dynamic sealings modeling, the reader is referred to [25–29].

2. Problem Formulation

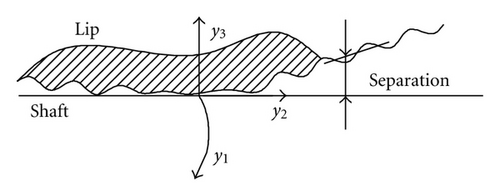
Here we consider a generic rough compliant solid in steady sliding contact with a rigid smooth counter surface, as shown in Figure 1(a). Due to the coupled action of asperity-fluid and asperity-asperity interactions, the compliant surface gains the actual (or deformed) configuration (Figure 1(b)). In soft-contacts, the shape difference between the deformed and initial configurations cannot be usually neglected, due to the occurrence of large deformations. Nevertheless, the small displacement assumption is usually adopted in the literature of soft-elastohydrodynamics [6, 30, 31] (soft-EHL), supported by a relevant experimental validation for ball-on-flat contact geometries. However, if one analyses the contact at much shorter length scales, that is, at the asperities length scales, then one finds out that the asperities may be completely flattened because of the high contact and fluid pressures. Hence, neglecting the influence of large deformation would lead to strong inaccuracy in describing the evolution of the system at the micro-scales. For this reason, in this work, the small displacement assumption has been relaxed. Moreover, in some cases, for example, for dynamic sealings modeling, the precise calculation of the large tangential displacement of the rubber at the interface of the sliding contact is a must in order to capture key phenomena as the well known reverse pumping effect [26].

Details are in the caption following the image
Figure 1 (a)   Initial configuration
Open in figure viewerPowerPoint
Contact scheme: (a) reference geometry; (b) deformed geometry obtained by solving the fluid/solid contact problem.
Details are in the caption following the image
Figure 1 (b) Deformed configuration
Open in figure viewerPowerPoint
Contact scheme: (a) reference geometry; (b) deformed geometry obtained by solving the fluid/solid contact problem.
Consider now the schematic drawing of Figure 1(a). We assume that the whole texture belongs to the class of Reynolds roughness, that is, with 〈|∇h|2〉 ≪ 1 (where h is the surface height distribution). In such a case, the thin film lubrication formulation is sufficiently accurate in describing the fluid dynamics at the sliding interface at all roughness lengths. The (ensemble) average local separation, is calculated as:
()
where xi and yi (the subscript i = 1 or 2 or 3, see Figure 1(b)) are the three coordinates of the lip surface points at the initial (xi) and at the deformed (yi) state respectively. The quantity ur represents the macroscopic contact shape and hr the undeformed low-pass filtered (i.e., for λ > λth) surface roughness. wi is the generic component of the displacement vector describing the average local surface deformation of the compliant body. In the classical EHL approach the displacement wi is calculated within linear elasticity framework [31], by adopting a boundary element approach which requires O(n2) operation where n is the number of discretization points. In our case, however, we adopt a more general nonlinear rheology and the displacement components
()
are calculated by employing a classical finite-element solver, which requires O(n3) operations. Observe that the normal (locally averaged) stress σ3(y) is (see also [6])
()
where y = (y1, y2, y3), σf3(y) is the locally averaged fluid pressure and σs3(y) the locally average solid contact pressure, the latter coming from the asperity-asperity interactions occurring at length-scales λ < λth. We observe that [6]:
()
where Ac(y)/A0 is the local normalized area of solid contact, where τf is the average fluid shear stress (see later for more details). We assume that the solid friction shear stress τs is constant (and directed along the sliding direction), as it happens in the case for a rubber-inert substrate contact [6]. Clearly, the model can be easily extended to include different boundary friction conditions.
The relation between the average solid contact pressure σs3 and the local average interfacial separation is obtained from Persson’s theory of contact mechanics [32, 33]. In particular, given the local elastic properties of the material and the power spectral density (PSD, see, e.g., Figure 2) of the surface (h is the surface roughness field, with average value 〈h(x)〉 = 0, q0 = 2π/λ0, where λ0 is the low frequency cut-off wavelength), the theory allows to calculate the local areal fraction of solid-solid contact αc = Ac/A0 as a function of the locally averaged solid-solid contact pressure σs3 as
()
where the quantity is the root mean square gradient of the rough surface and is related to the PSD C(q) of the rough surface through the formula . The relation between the local interfacial separation and the solid-solid contact pressure is instead determined, in the adhesionless case, by requiring that the change of elastic energy per unit nominal contact area dUel at the interface equals the work done by the contact pressure to deform the elastic body:
()
In (6) the elastic energy per unit contact area Uel is calculated as a function of the contact pressure σs3 (see [32, 33] for more details). The final formula linking the local separation and the solid-solid contact pressure is relatively complicated, but at large separation it simplifies and becomes [33]
()
where the quantities β1 and β2 can be easily calculated once the PSD of the rough surface is known [33], and E* = E/(1 − ν2).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
A self-affine power spectral density of a generic surface roughness. Points correspond to that spectral content included deterministically in the calculations, whereas the continuous line represents the homogenized surface roughness.
We consider now the case where a Newtonian fluid is sandwiched at the interface between the solids. We assume constant viscosity η, constant density ρ, and isothermal conditions. The adoption of a Reynolds roughness, and the assumption of a representative average interfacial separation value , suggests that the fluid velocity varies slowly with the coordinates y1 and y2 compared to the variation in the orthogonal direction y3. In such a case, combining the equilibrium with the continuity equation, the homogenized problem formulation reads [9, 34]
()
where, as before, and σf3 are the locally averaged (over a length scale given by the longest wavelength surface roughness component, i.e., λth) interfacial surface and fluid pressure, respectively. The fluid flow conductivity (tensor) σeff and can be related, respectively, to the pressure flow factor (tensor) [7, 9, 35, 36] and to the shear flow factor (tensor) , which we assume to be a function of the average interfacial separation only. Here ϕp has been calculated on the basis of the Bruggeman’ effective medium theory and on the Persson’s contact mechanics [34]. Within this approach, the effect of solid contacts percolation, as well as of local fluid trapping, on the fluid flow can be taken approximately into account, as recently discussed in [16]. For simplicity, we have assumed ϕp = ϕpI, and ϕs = I, where I is the identity tensor. Moreover, by considering the steady sliding condition, the homogenized lubricant equation simplifies into:
()
where U = 2Um is the sliding velocity.
However, in order to include the effect of micro-cavitations occurring at large-scale roughness lengths, a JFO cavitation model (constant mixture pressure in the cavitation zone) is adopted. The Reynolds equation is then reformulated under a mass conservative equation valid throughout the cavitating/not cavitating domain:
()
where we have adopted the cavitation index F (F = 0 in the cavitation zones, and F = 1 otherwise) and the dummy variable ϕ defined as
()
where ρ0 is the lubricant density, and G is the representative solid shear elastic modulus. Note that (10) must be solved on the deformed configuration, which is an unknown of the problem: therefore, reformulating the fluid equation in the initial configuration may result numerically convenient. Thus (10) has been rephrased by using the mapping rule
()
The Jacobian J = ∂(x1, x2)/∂(y1, y2) of the transformation can be calculated as the inverse J = g−1 of the Jacobian g = [gij] = ∂(y1, y2)/∂(x1, x2) of the transformation
()
Observe that the determinant of the Jacobian tensors must be necessarily larger than zero, that is, det g = (det   J)−1 > 0. The above transformation enables the generation of an adaptive mesh grid which follows the changing of the surface shape during the deformation process, thus without loosing spatial resolution. The detailed numerics derivation is reported in the Appendix.
The boundary conditions to be applied in the resolution of (10) depend, clearly, on the particular soft-contact problem under investigation. The dimensionless formulation of (10) is
()
where and α = 2hrms/λ0 = q0hrms/π (note that has been made dimensionless with hrms, whereas other lengths with λ0). λ0 corresponds in this case to the largest deterministic roughness wavelength.

3. Results

In this work we use the proposed model to investigate the lubricated contact of the lip seal schematically shown in Figure 3. Moreover, being λ0 much smaller than the shaft diameter, it is possible to reduce the computational domain to only a small angular fraction of the lip surface. Therefore, (10) is solved with the constant pressure boundary conditions at the low pressure side p = penv and at the high pressure side p = poil, and with the periodicity conditions on the circumferential y1-direction, with spatial period λ0. The two-scale mixed lubrication model has been numerically solved, as described in the Appendix. We have opted for a fractal self-affine isotropic geometry. For any self-affine fractal surface the statistical properties are invariant under the transformation
()
In such a case it can be shown that for isotropic surface the PSD is
()
where q0 = 2π/λ, q = |q|, H is the Hurst exponent of the randomly rough profile, which is related to the fractal dimension Df = 3 − H. To apply our method we need to numerically generate the surface hr(x) in the low frequencies spectrum, that is, for ζ > ζth, see, for example, Figure 2. To this end we have utilized the spectral method described in [37] where the roughness is described by a periodic surface in the form of Fourier series
()
where qkh = (kq0, hq0), x = (x, y). Since hr(x) is real we must have . Moreover for randomly rough surfaces the following relation must be satisfied 〈ahkalm〉 = 0 with l ≠ ±h, m ≠ ±k, where the symbol 〈⋯〉 is the ensemble average operator. The PSD of Surface Equation (17) is
()
from which it follows:
()
For isotropic surfaces we have C(q) = C(q) which simply gives and assuming self-affine fractal surface (see (16)) one obtains
()
Hence the quantities can be determined once and the Hurst exponent of the fractal surface are known. However to completely characterize the rough profile we still need the probability distribution of the quantities ahk. We first observe that the condition 〈ahkalm〉 = 0 with l ≠ ±h, m ≠ ±k is satisfied if the phases φhk of the complex quantities ahk are random numbers uniformly distributed between 0 and 2π. We also recall the condition also implies that |a−h,−k| = |ah,k| and that the quantities φ−h−k = −φhk. So what we need now is only the probability distribution of |ah,k|. Of course there are several choices and the simplest one is to assume that the probability density function of |ahk| is just a Dirac’s delta function centered at , that is,
()
It can be shown that this choice guarantees also that the random profile h(x) has a Gaussian random distribution.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
A schematic of a typical lip seal construction. A garter spring enables the radial compression of the seal lip on the shaft surface, ideally preventing fluid leakage from the high pressure side (the fluid reservoir) to the low pressure side. In the running-in stage, the seal lip is macroscopically reshaped as a consequence of the initial lip wear process, which depends on the seal-shaft designed interference and on the solids chemical and physical affinity with the actual lubricant composition. After this bulk material removal (and depending on the viscoelastic rubber properties), a successful seal reaches a steady-state configuration with a well defined roughness pattern, strongly dependent on the actual shaft micro-geometry, and with an established thin lubricant film at the interface.

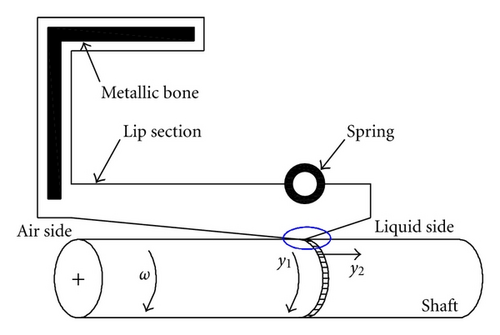
3.1. Sealing at Nearly Zero Sliding Velocity

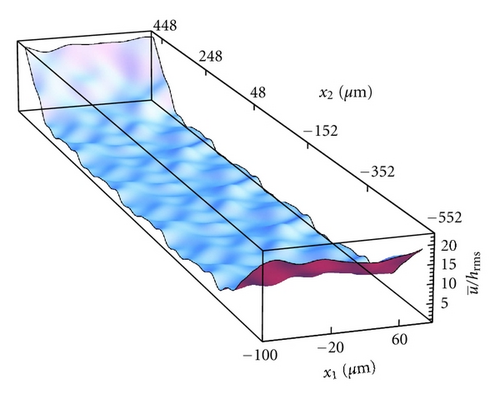
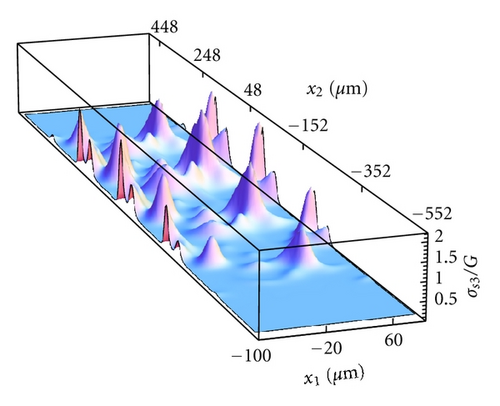
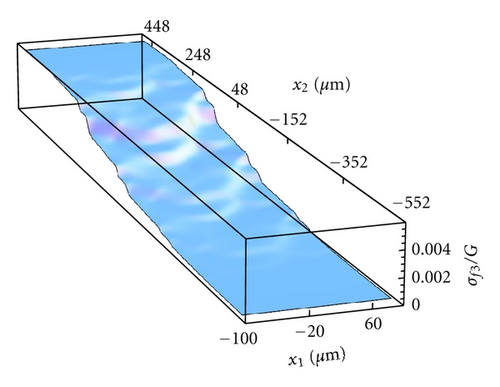
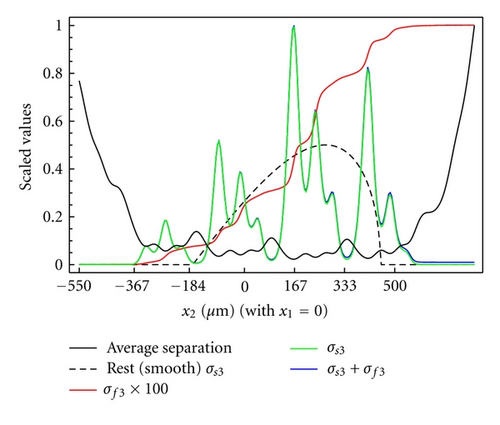
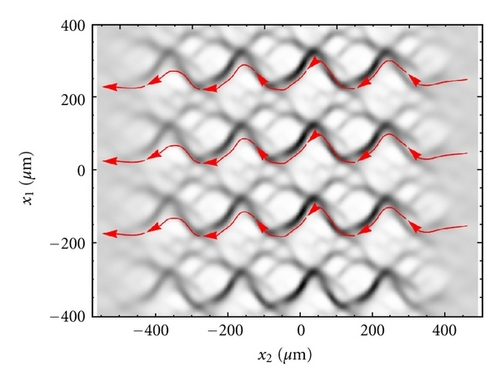
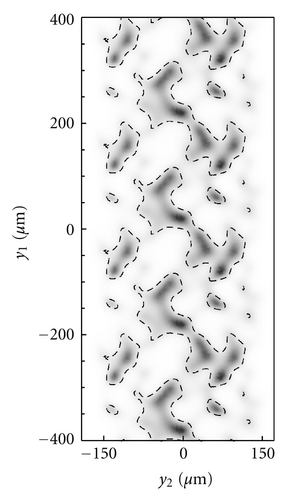
Here we report on the model application to the case where the sliding velocity between the two mating surfaces is vanishing (), that is, for the case of static seals. The self-affine roughness of the lip surface presents a long-distance cut-off frequency q0 = 2π/200 μm−1, fractal dimension Df = 2.4, , and small scale cut-off frequency q1 = 1000q0. The threshold frequency adopted in the calculation is qth = 2π/λth = 5q0. In the following, the seal is assumed linear elastic. The calculation is performed at a constant rigid penetration of the lip. In Figure 4 we show the locally averaged interfacial separation field (note that x1 is the circumferential direction, whereas x2 is the axial direction). Interestingly the corrugation which can be observed in the figure is just a consequence of the deterministically included roughness (ζ < ζth), at larger frequency the surface appears smooth since the high frequency (ζ < ζth) content of the roughness has been included through Persson’s statistic model, that is, by means of homogenization. The corresponding average solid contact pressure is shown in Figure 5(a). Observe first that, due to the presence of roughness, the contact is split into many contact patches in the whole lip apparent contact area and, correspondingly, normal stresses are concentrated into contact spots. Observe also that the average solid contact pressure is smooth at the contact borders, differently, from what instead expected in the case of smooth elastic contact (e.g., in the case of the Hertzian contact). This is due to the homogenized roughness contribution, which distributes, on a wider local contact area, the pressure acting on the single deterministic asperity. The average fluid pressure is shown in Figure 5(b). Observe that the fluid pressure presents steep variations (almost step-like) in those locations where the separation between the surfaces takes the smallest values. This is in perfect agreement with the critical junction theory of leakage in seals [8], which predicts that the hydraulic resistivities are only concentrated in few points where the fluid flow encounters strong restrictions. At these restrictions the pressure must present high gradients as clearly shown in Figures 5(b) and 6. In particular, in Figure 6 we report the average interfacial separation (black curve), the average solid contact pressure (green curve), the average fluid pressure (red curve), the total average normal stress (blue curve, slightly distinguished from the average solid contact pressure), and the solid contact pressure in the case of perfectly smooth contact (black dashed curve, useful for comparison), for x1 = 0 (i.e., along the axial direction). Note that the largest pressure gradients occur in the very proximity of the largest values of σs3, that is, where the local average separation takes its minimum value. It is also interesting to observe the normalized solid contact area Ac/A0 for this static contact case, see Figure 7(a). Note that, due to the high local squeezing pressure, the asperities low-frequency features (i.e., the roughness asperities described by the deterministical model) have been squeezed so much to coalesce in larger contact patches. Figure 7(b) shows a sample of the leakage flux lines calculations (red lines) superposed to the locally averaged fluid velocity intensity (in gray scale). As expected [8], the presence of asperity-asperity contacts increases the hydraulic resistivity at the interface and, in particular, largest values of fluid velocity occur at the local minimum in the average interfacial separations.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Dimensionless average interfacial separation as a function of contact position, reported in the undeformed reference.
Details are in the caption following the image
Figure 5 (a) Average solid contact pressure σs3
Open in figure viewerPowerPoint
Average fluid and solid contact pressure for the static linear elastic seal.
Details are in the caption following the image
Figure 5 (b) Average fluid pressure σf3
Open in figure viewerPowerPoint
Average fluid and solid contact pressure for the static linear elastic seal.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
All solutions in arbitrary scaling.
Details are in the caption following the image
Figure 7 (a) Normalized solid contact area Ac/A0
Open in figure viewerPowerPoint
Static sealing effectiveness.
Details are in the caption following the image
Figure 7 (b) Sample of fluid flux lines
Open in figure viewerPowerPoint
Static sealing effectiveness.

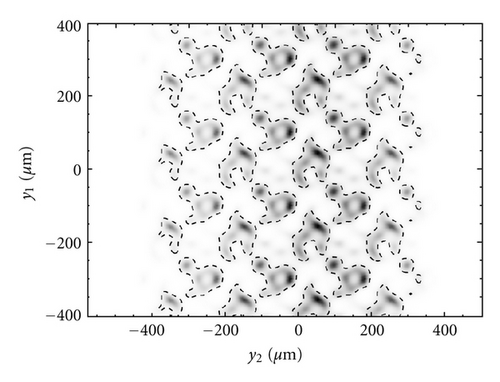
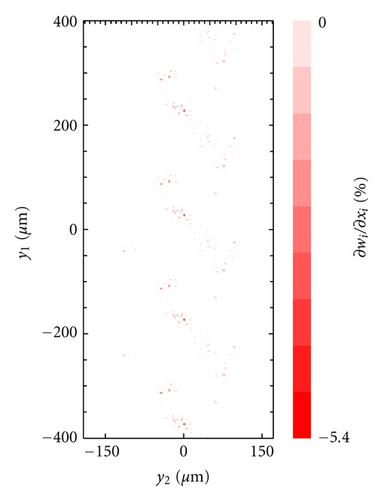
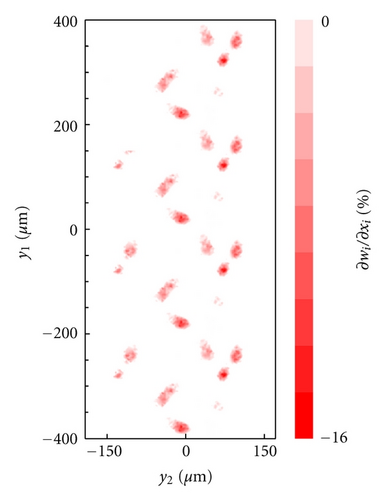
We have also carried out calculations assuming the seal obeys a Mooney-Rivlin model. The results are then compared with the elastic case. In Figure 8 we show the normalized area of real contact for the elastic (Figure 8(a)) and hyperelastic (Figure 8(b)) bulk rheology. Observe that for the linear case, the area of contact are slightly larger, as expected, then for the other case. This however, does not strongly affect the leakage flow for the current geometry, as shown in Figure 9. However, interestingly, the nonlinear rheology is characterized by a larger value of surface area change, evaluated as ∂w1/∂x1 + ∂w2/∂x2 (see Figure 10), where we show in red colors that on part of the interaction domain there is a shrinking, that is, ∂w1/∂x1 + ∂w2/∂x2 < 0. Observe that in plane surface displacements are responsible for the frequency-shift of roughness PSD, for example, in the case of Figure 10(b) we expect a relevant modification of the homogenized power spectral density shape, which can therefore affect the local contact mechanics and flow factors. In the literature, surface displacements are not usually taken into account; however the present study shows that such a surface effect can be relevant for contact modeling.

Details are in the caption following the image
Figure 8 (a) Linear elastic
Open in figure viewerPowerPoint
Normalized area of real contact for different bulk rheologies. Dashed contours represent the bearing area paths.
Details are in the caption following the image
Figure 8 (b) Mooney-Rivlin
Open in figure viewerPowerPoint
Normalized area of real contact for different bulk rheologies. Dashed contours represent the bearing area paths.
Details are in the caption following the image
Figure 9 (a) Linear elastic
Open in figure viewerPowerPoint
Sample of leakage flux lines.
Details are in the caption following the image
Figure 9 (b) Mooney-Rivlin
Open in figure viewerPowerPoint
Sample of leakage flux lines.
Details are in the caption following the image
Figure 10 (a) Linear elastic
Open in figure viewerPowerPoint
In-plane area shrinking.
Details are in the caption following the image
Figure 10 (b) Mooney-Rivlin
Open in figure viewerPowerPoint
In-plane area shrinking.

3.2. Sealing at Non-Zero Sliding Velocity

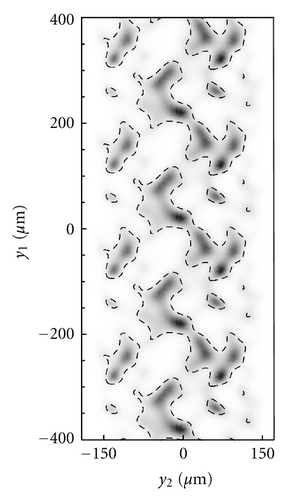
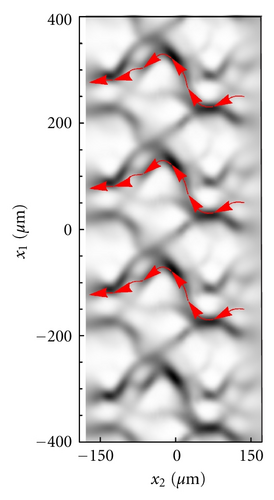
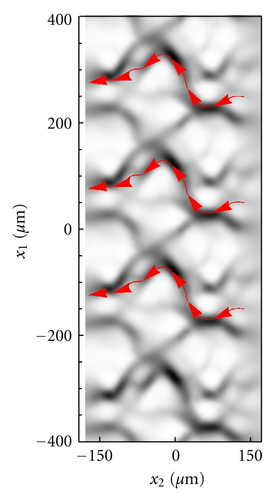
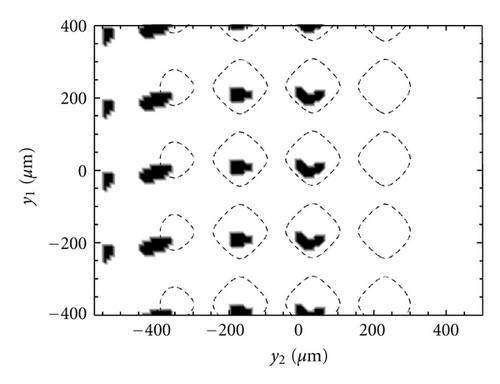
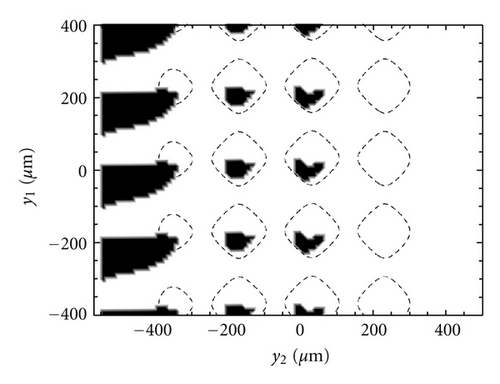
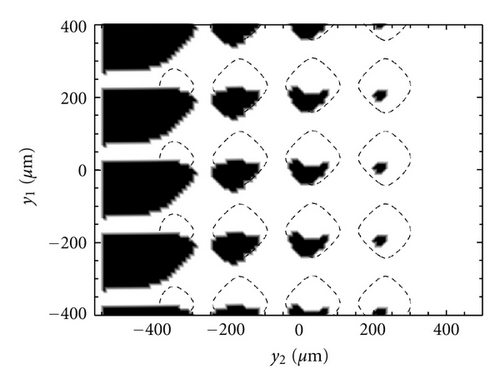
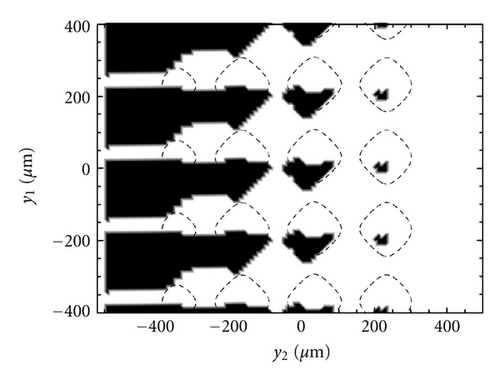
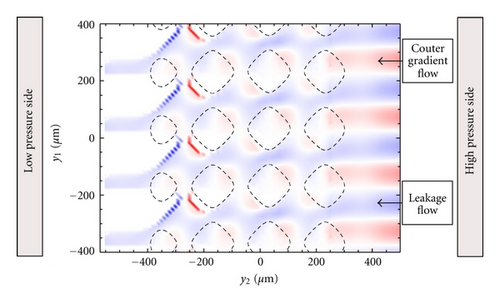
In this section we show the case of non-zero sliding velocity. The macroscopic lip geometry is the same as before, as well as the roughness PSD. However, this time the part of roughness that is described deterministically is characterized by only one length scale, that is, just one frequency is included. The remaining roughness has been therefore included within the homogenized approach. In Figure 11 we show the cavitation areas (black areas), occurring over a circumferential portion of the lip-shaft macroscopic contact domain. Results are shown at different values of dimensionless sliding velocity. Interestingly, cavitation originates as expected in the low pressure side of the region (i.e., on the left side of the domain, whereas sliding velocity is directed from top to the bottom) and at the trailing edge of asperities. By increasing the sliding velocity, the cavitation extends from the low to the high pressure side. The cavitated areas may even coalesce at the largest sliding velocity, with the formation of cavitation fingers shown in Figure 11(e). The adoption of our two-scale approach allows then to capture the complex solid contact and fluid-dynamics characteristics of real contact geometry, which can help engineers to have useful insights into the mixed-EHL lubrication condition occurring at the interface of soft-contacts, especially in terms of friction and leakage, with much less computation effort. Figure 12 shows the axially component of fluid flow at the interface. Red areas corresponds to the counter-gradient flow (i.e., the flow directed in the opposite direction compared to the externally applied fluid pressure gradient). Observe that, on the high-pressure side, due to the asperities presence, a certain fluid recirculation is observed which tends to hamper the observed net leakage (blue fingers in the low-pressure side). The recirculation is due to the effect of fluid depressurization which occurs at the divergent part of the single asperity/substrate interfaces. This depressurization determines a relevant fluid suction from the high pressure side which is partially balanced by the flow induced by the counter-pressure gradient.

Details are in the caption following the image
Figure 11 (a) U~=100
Open in figure viewerPowerPoint
Cavitation domains (black areas) for different dimensionless sliding velocities.
Details are in the caption following the image
Figure 11 (b) U~=200
Open in figure viewerPowerPoint
Cavitation domains (black areas) for different dimensionless sliding velocities.
Details are in the caption following the image
Figure 11 (c) U~=400
Open in figure viewerPowerPoint
Cavitation domains (black areas) for different dimensionless sliding velocities.
Details are in the caption following the image
Figure 11 (d) U~=800
Open in figure viewerPowerPoint
Cavitation domains (black areas) for different dimensionless sliding velocities.
Details are in the caption following the image
Figure 11 (e) U~=1600
Open in figure viewerPowerPoint
Cavitation domains (black areas) for different dimensionless sliding velocities.
Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Axial average flows. Red areas correspond to the counter-gradient flows (i.e., directed from left to right). For .

4. Conclusions

We have presented a novel two-scale approach for the description of the mixed lubrication regime for real soft-contacts. We modeled the asperity-asperity and asperity-fluid interactions with a deterministic or a statistical approach (DSA) depending on length scale at which the contact region is observed. The roughness at large length scales, which mainly determines the fluid flow at the interface, is deterministically included in the model while the roughness at short wavelengths, which strongly contributes only to the friction, is included by means of a homogenization process (recently developed in [9]). We have applied the DSA to lip sealings contact mechanics modeling, and we have analyzed the mixed lubrication characteristics at nearly-zero and non-zero shaft sliding velocity. In the case of nearly-zero sliding velocity the lip seal behaves as a classical static seal, and we showed that the fluid flow at the interface is determined only at the smallest constrictions along the leakage path, in agreement with recent developments of static seals theory. In the case of non-zero sliding velocity, we showed the occurrence of micro-cavitations and cavitation fingers, whereas leakage has been shown to be associated to asperity-induced fluid suction at the high pressure side (for the given geometry). Finally, we note that DSA-based mixed lubrication models, which belong to the class of multiscale contact mechanics models, provide a high-resolution description of very complex contact problems with a reduced or, at least, tunable computational effort, opening the perspective for its application in general purpose engineering software.

Nomenclature

  • η:
  • Fluid viscosity
  • ν:
  • Poisson’s ratio
  • α:
  • Reduced root-mean-square roughness
  • αc:
  • Local normalized area of solid contact
  • :
  • Locally averaged interfacial separation
  • β1:
  • Parameter for the asymptotic interfacial separation law
  • β2:
  • Parameter for the asymptotic interfacial separation law
  • λth:
  • Threshold roughness wavelength
  • ρ0:
  • Full film density
  • :
  • Shear flow conductivity
  • σ3:
  • Normal (locally averaged) stress
  • σeff:
  • Pressure flow conductivity
  • σf3:
  • Normal (locally averaged) fluid stress
  • σs3:
  • Normal (locally averaged) solid contact stress
  • τfi:
  • Tangential (locally averaged) fluid stress i-component
  • τi:
  • Tangential (locally averaged) stress i-component
  • τsi:
  • Tangential (locally averaged) solid contact stress i-component
  • :
  • Reduced sliding velocity
  • ζ:
  • Roughness magnification or wavenumber
  • ζth = L0/λth:
  • Threshold roughness wavenumber
  • A0:
  • Representative area of interaction
  • Ac:
  • Area of solid contact in A0
  • C(q):
  • Total roughness power spectral density
  • Csto(q):
  • Power spectral density of the statistically-calculated roughness
  • E:
  • Young’s modulus
  • E*:
  • Reduced elastic modulus
  • F:
  • Cavitation index
  • G:
  • Shear elastic modulus
  • gij:
  • Mapping rule Jacobian
  • hr:
  • Deterministic surface roughness height function
  • Jij:
  • Inverse of the mapping rule Jacobian
  • L0:
  • Representative macroscopic size of the contact
  • U:
  • Shaft sliding velocity
  • Um:
  • Mean velocity
  • ur:
  • Macroscopic contact shape function
  • Uel:
  • Locally stored elastic energy
  • wi:
  • Generic component of the average surface displacement vector
  • xi:
  • Initial state reference
  • yi:
  • Actual or deformed state reference.

    • Acknowledgment

    The authors acknowledge Regione Puglia for having supported part of this research activity through the constitution of the TRASFORMA Laboratory Network cod. 28.

      Appendix

      Equation (10) has been discretized with the control volume approach. In particular, (10) can be integrated in a portion of the contact area considering that the elementary area
      ()
      gives
      ()
      where
      ()
      The forward difference for the Couette term has been used in order to get a stable scheme, in conjunction with the adoption of the Gauss-Seidel technique.
      The average fluid shear stresses in the fluid zones can be calculated as:
      ()
      whereas in the cavitation zones:
      ()

      The resolution scheme is summarized in Figure 13. The contact model is split into two, coupled problems, respectively, the deterministic and the homogenized problem. Given the macroscopic gap relation , the average surface stress is determined by solving the homogenized part, which consists of the Persson’s contact mechanics and of the homogenized fluid problem (previously discussed). The deterministic part follows, where the macroscopic deformation problem is solved as a function of the previously calculated average surface stress field. To do so, in this work we have used the Ansys finite element code; in particular, the lip geometry, similar to that described in [27], has been meshed with tetrahedral structural elements of type 92. The macroscopic gap relation is then finally updated, determining the loop restart. The solver iterates until certain convergence criteria are satisfied. In our case, convergence is checked on the average interfacial separation field . Under-relaxation, with relaxation factors in the range [0.01,0.1], is usually adopted to numerically damp the interfacial separation solution.

      Details are in the caption following the image
      Figure 13
      Open in figure viewerPowerPoint
      Algorithm scheme. In the two-scales approach, the solution of the contact problem is split into two, coupled problems, respectively, the deterministic and the homogenized problem. Those are solved iteratively towards convergence.

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.