Discrete Dynamics in Nature and Society
Volume 2012, Issue 1 412052
Research Article
Open Access

On the Solution of a Class of Nonlinear Systems Governed by an M-Matrix

Woula Themistoclakis, 

Woula Themistoclakis

Istituto per le Applicazioni del Calcolo “Mauro Picone”, Sede di Napoli, National Research Council of Italy (CNR), Via P. Castellino, 111, 80131 Napoli, Italy cnr.it

Search for more papers by this author
Antonia Vecchio, 

Corresponding Author

Antonia Vecchio

Istituto per le Applicazioni del Calcolo “Mauro Picone”, Sede di Napoli, National Research Council of Italy (CNR), Via P. Castellino, 111, 80131 Napoli, Italy cnr.it

Search for more papers by this author
First published: 08 June 2012
https://doi.org/10.1155/2012/412052
Citations: 7
Academic Editor: Rigoberto Medina

Abstract

We consider a weakly nonlinear system of the form (I + φ(x)A)x = p, where φ(x) is a real function of the unknown vector x, and (I + φ(x)A) is an M-matrix. We propose to solve it by means of a sequence of linear systems defined by the iteration procedure (I + φ(xr)A)xr+1 = p, r = 0, 1, …. The global convergence is proved by considering a related fixed-point problem.

1. Introduction

In recent years [1, 2], we approached the numerical resolution of the following nonstandard integrodifferential problems arising in the study of the kinetic theory of dusty plasmas:
(1.1)
whose discretization, by means of a difference scheme and a quadrature rule [2], leads to a particular kind of nonlinear system of equations. Solving it by means of a fixed-point (FP) iteration process, we noted that such a procedure seems to globally converge, that is, it converges independently of the choice of the starting point. Our aim, here, is to explain the reason of this “nice” behavior. Throughout the paper, the notation M ≥ 0, with M ∈ RN×K, means that each element of M is nonnegative, whereas M > 0 means M ≥ 0 and M ≠ 0. The nonlinear system under investigation is
(1.2)
where I is the N-dimensional identity matrix, x ∈ RN is an unknown vector, and we make the following assumptions which will be sufficient for the global convergence of the iterative process we propose (see Theorem 3.3):
  • (i)

    p ∈ RN  with p > 0;

  • (ii)

    A ∈ RN×N has nonnegative main diagonal and nonpositive off-diagonal entries (Z-matrix);

  • (iii)

    A is rowwise weakly diagonal dominant;

  • (iv)

    φ : RN → R is a differentiable function such that φ(x) ≥ 0, for all x ≥ 0 and it is homogeneous of degree γ ≤ 1, that is, for all α > 0  φ(αx) = αγφ(x);

  • (v)

    grad(φ(x)) > 0  for  all  x ≥ 0, where grad(φ(x)) denotes the (row vector) gradient of φ(x).

Systems of type (1.2) fall into the class of weakly nonlinear systems (see, e.g., [3, 4]) and they also arise from the discretization, by finite-difference methods, of mathematical models less cumbersome than (1.1), as, for instance, the differential problems of the form:
(1.3)

A central rule in our results is played by the matrix (I + φ(x)A) appearing in (1.2) which, as it can be immediately seen from the assumption (ii)‒(iv), is an M-matrix for  all  x ≥ 0 (see, e.g., [5, page 137, prop. M35]).

The organization of the paper is the following. In Section 2, we investigate a particular class of one variable functions f such that the FP iterations tr+1 = f(tr) converge independently of the choice of the starting value t0. By exploiting this result jointly with the properties of the matrix I + φ(x)A, we are lead to state that, under the assumptions (i)–(v), the FP iteration procedure (I + φ(xr)A)xr+1 = p globally converges to a solution of (1.2). This constitutes our main result which is contained in Section 3. Finally, some numerical experiments showing the sharpness of the required conditions and the performance of the iteration scheme are reported in Section 4.

2. The One Variable Case

In order to prove our main theorem, we need the following result on a particular class of numerical sequences.

Theorem 2.1. Let f be a one variable scalar function such that

  • (a)

    f : t ∈ X⊆[0, +∞)→(0, Mf), with Mf > 0, X closed and f(X) ⊂ X;

  • (b)

    f continuous;

  • (c)

    tf(t) strictly increasing.

Then, starting from any t0 ∈ X, the sequence obtained by the functional iteration process
(2.1)
converges to t*, a fixed point of f.

In this section, we are going to prove this theorem.

Denote by g the function g(t) = t − f(t), then we have
(2.2)
Of course, if there exists a point tr such that g(tr) = 0, then tr = tr+n for all n = 0,1, … and the statement is trivial. Similarly, if the sequence g(tr) is ultimately nonnegative (nonpositive), we have that the sequence tr is ultimately decreasing (increasing) and it trivially converges by hypothesis (a). Therefore, from now on, we assume that the sequence g(tr) satisfies
(2.3)
The following lemma holds.

Lemma 2.2. If g(tr) < 0  (resp. > 0) and g(tr+m) > 0  (resp. < 0), m = 1, …, n, then

(2.4)

Proof. Let us prove (2.4) by induction on n ≥ 1. Assume n = 1, that is, we are assuming that

(2.5)
and we want to prove
(2.6)
From the first of (2.5) and (2.2), we immediately get (2.6) with m = −1, that is, we have
(2.7)
and so, from the hypothesis (c), we deduce
(2.8)
which, recalling that f(tr) = tr+1, implies
(2.9)
and, therefore, (2.6) holds with m = 0, that is,
(2.10)
By using (c) once again, (2.10) gives trf(tr) < tr+2f(tr+2) or equivalently
(2.11)
But the second of (2.5) implies tr+2 < tr+1, so that from (2.11), we obtain
(2.12)
which assures that (2.6) holds for m = 1 too.

Now, we assume that the lemma holds for m = n, that is, suppose that

(2.13)
implies
(2.14)
In order to prove the lemma for m = n + 1, assume
(2.15)
Of course (2.14) holds, and the second of (2.15) implies
(2.16)
But from (2.14) with m = n and (c), we have
(2.17)
which in view of (2.16) leads to
(2.18)
Hence, tr < tr+n+3, that is, (2.14) holds for m = n + 1 too, and the desired result is proved.

Now, let us partition the sequence {tr} r into two subsequences and defined by
(2.19)

In order to state Theorem 2.1, we are going to prove that these subsequences converge to the same limit. First of all, the following result holds.

Lemma 2.3. The sequences and are strictly increasing and decreasing respectively.

Proof. Let us prove that the sequence is strictly increasing, the proof about is analogous, and it is omitted. Consider ri such that . Then, two cases may occur: (I) or (II) .

  • (I)

    In this case, it is clear that belongs to the same subsequence and we immediately have

    (2.20)

  • (II)

    From (2.3), there exists n ≥ 2 such that , that is, we have

(2.21)
Then, Lemma 2.2 with r = ri assures that
(2.22)
which, for m = n − 2 ≥ 0, gives
(2.23)
The desired result comes out from (2.20) and (2.23).

Lemma 2.4. The sequences and provide two separate sets, that is,

(2.24)

Proof. Suppose, for example, ri < sj and precisely let sj = ri + k. If k = 1, we get (2.24) directly from the assumption . If k ≥ 2, observe that the numerical sequence presents at least one change of sign, in view of (2.19). Let us examine the case of an unique change of sign, by supposing that there exists an integer l, with 0 ≤ l ≤ k − 1, such that

(2.25)
the other cases being analogous.

By Lemma 2.3, we get

(2.26)
and by applying Lemma 2.2 with r = ri + l, we deduce
(2.27)
Hence, by taking m = k − l − 2 ≥ −1, we conclude
(2.28)

By the previous lemmas, we get the next result which completes the proof of the convergence of the FP iteration process.

Theorem 2.5. For any choice of t0 ∈ X, the sequence {tr} r defined in (2.1) converges.

Proof. It is sufficient to prove that the subsequences and defined in (2.19) converge to the same limit, satisfying

(2.29)
By the previous lemmas, we partitioned the sequence {tr} into two subsequences, and , which are separate, strictly monotone, and bounded sequences. Hence, they converge and
(2.30)
Assume ab absurdo that
(2.31)
Let us consider the subsequence of and the subsequence of , such that
(2.32)
In other words, and are those elements of and , respectively, whose previous elements, in the main sequence {tr}, belong to the other subsequence and respectively, that is, we have that
(2.33)
Of course, as is a subsequence of the convergent sequence , there results
(2.34)
and the same is true for , that is,
(2.35)
where l1 and l2 are given in (2.30). On the other hand, recalling that , from (b) and (2.33), we have
(2.36)
But by the hypothesis (c), the assumption (2.31) implies l1f(l1) < l2f(l2), that is, in view of (2.36), we have l1l2 < l2l1, which is absurd. Thus, the result l1 = l2 = lim rtr is achieved.

3. The Solution of the Nonlinear System

In this section, we come back to the nonlinear system (1.2). First of all, we recall that, under the hypotheses (ii)–(iv), for any x ≥ 0, the matrix (I + φ(x)A)) appearing in (1.2) is an M-matrix and it satisfies (see, e.g., [5, prop. N38])
(3.1)
Now, we define the function F as
(3.2)
and we are going to prove that it satisfies the properties stated in the following theorem, where γ is the homogeneity degree of φ appearing in (iv) and the classical notation e = (1, …, 1) T ∈ RN is used.

Theorem 3.1. Assume that (i)–(v) hold. Then, F is a continuous, differentiable function, and for any q ≥ 0, it satisfies

(3.3)
(3.4)
(3.5)

Proof. As the inverse of (I + qA) is defined for all q ≥ 0, then F is clearly a continuous function. Moreover, it can be easily seen that

(3.6)
hence, (3.4) is immediately true. In view of Theorem A.1 in [6], we observe that (ii) and (iii) assures
(3.7)
Therefore, for any q ≥ 0, the vector x(q): = (I + qA) −1p satisfies ∥x(q)∥∞ ≤ ∥p∥∞ and because of (v), we get F(q) = φ(x(q)) ≤ φ(∥p∥∞e). Consequently, assertion (3.3) holds taking into account (iv). Finally, again in view of (iv), we have
(3.8)
where, recalling (3.6), it results
(3.9)
Thus, by (v) and (3.1), we deduce (3.5) from
(3.10)

Using this theorem, we can easily claim that the function F in (3.2) has the same characteristics as the function f introduced in the previous section.

Corollary 3.2. Assume that (i)–(v) hold. Then, the function F verifies all the hypotheses (a)–(c).

Proof. Assertions (a) and (b) directly follow from Theorem 3.1. Moreover, in view of (3.5), (c) is immediately obtained by qF(q) = s(q)q1−γ, recalling that γ < 1 implies q1−γ strictly increasing.

Now, we are ready to state our main result about the convergence of the sequence {xr} defined as
(3.11)

Theorem 3.3. Assume that the hypotheses (i)–(v) hold. Then, the sequence {xr} converges to a solution x* of (1.2).

Proof. Let us start from an arbitrary x0 ≥ 0 and put

(3.12)
From (3.11), we have that (3.12) can also be written as qr+1 = F(qr), r = 0,1, … Therefore, Corollary 3.2 assures that the sequence {qr} is convergent. Denoted by q* its limit, we set x* : = (I + q*A) −1p, and we obtain the statement by observing that
(3.13)

Remark 3.4. Of course, in view of (3.7), any solution of (1.2) satisfies ∥x*∥∞ ≤ ∥p∥∞, but nothing seems to imply its uniqueness. Anyway, we conjecture it, because in a large variety of experimental tests (including also high-dimensional systems), we never found more than one solution. Of course, a sufficient condition for the uniqueness is ∥grad(φ(x))∥1∥A∥∞∥p∥∞ < 1, for any x ≥ 0, which assures |F′(q)| < 1, for any q ≥ 0, by virtue of (3.4) and (3.7). Nevertheless, as it can be observed in the next section, it seems that the solution is unique even if such a condition is largely not satisfied.

4. Numerical Experiments

In order to verify our theoretical results and to check the performances of the FP iteration scheme on problem (1.2), we carried out a large variety of numerical experiments. Here, the most significant are reported. From the previous section, it appears clear that the iterative scheme (3.11), which furnishes a vector at each iteration, requires the same computational effort as (3.12), which instead provides scalar values. Hence, for the sake of simplicity, all the numerical tests reported here, are referred to (3.12), that is, we test the iterative procedure:
(4.1)
In particular, in all the section, we assume that the convergence is reached whenever |qr+1 − qr | < tol and we put tol = 10−6.
Let us consider the following two problems:
(4.2)
(4.3)
which, as it can be easily checked, satisfy the hypotheses of Theorem 3.3. In Tables 1 and 2, we report the number of iterations we performed in order to compute the fixed point q* of problems (4.2) and (4.3), respectively, for different choices of the starting value q0. Moreover, we also report the number of iterations performed by the Matlab routine fzero. This is given by the sum of the number of iterations to find an interval containing the zero (first addendum in Table 1) and the number of zero-finding iterations (second addendum in Table 1).
FP iterations. 15 14 14 15
q0 .2 .4 1 100
fzero iterations.   21 + 4     19 + 4     16 + 4     12 + 6  
FP iterations. 19 19 19 17 20
q0 .05 .1 1 2 100
fzero iterations. AB AB AB 11 AB
FP + fzero iterations.   1 + 13     1 + 15     1 + 12     3 + 4     2 + 13

From these two tests, we observe that, according to Theorem 3.3, the FP iteration method converges for any q0 in both the cases. Of course, when we know the interval where a zero lies, fzero does converge and it requires much less iterations, but in many cases this information is unavailable and, see Table 2, fzero fails to provide a value. In fact, at the third line of Table 2, the symbol AB stays for “aborted” and means that the MATLAB routine does not succeed in finding an interval containing a sign change. The last line of Table 2 shows that the best results can be obtained by a combined solution strategy, which starts with a certain number of FP iterations (first addendum) and takes the final steps using fzero iterations (second addendum). At the fifth column, we take the right balance between FP and fzero iterations, while in the remaining columns, we displayed the minimum number of FP iterations which are necessary to get a value from fzero. Thus, we can fruitfully exploit the global convergence of our FP iteration method in order to create more efficient combined strategy with fzero. Of course, this could be done also by means of other well-known methods like Newton’s one.

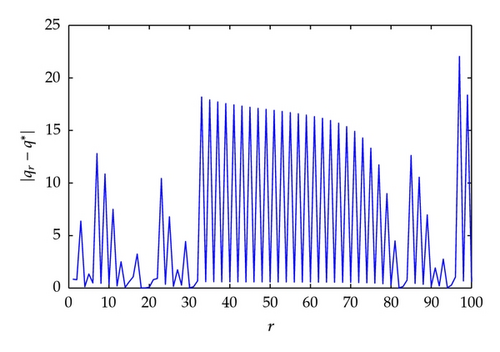
In order to verify whether the convergence of the FP procedure could be ascribed to the Banach contraction theorem, we plotted the absolute value of the derivative of the function F in (4.1) (not reported) and we noted that the starting value in bold, that is, q0 = .2, q0 = .4 in Table 1 and q0 = .05, q0 = .1 in Table 2, belongs to intervals where |F′(q)| > 1. Hence we can assert that, at least in these cases, the convergence of the FP method is not “helped” by the contraction principle.

As we already wrote in Remark 3.4, from these numerical experiments and many others, starting from very different values of q0, the method seems to converge to the same fixed point. For example, in problems (4.2) and (4.3), we obtain q* ≈ 4.7954 and q* ≈ 2.6085, respectively, for a very large number of initial guesses (much larger than the ones reported in Tables 1 and 2). This numerical evidence let us conjecture that the assumptions in Theorem 3.3 are also sufficient to assure the uniqueness of the solution of problem (1.2).

In Figures 1 and 2, we plotted the first 100 elements of the error sequence {|qr − q*|}, where qr is computed by applying the FP iterations to the following two problems:
(4.4)
(4.5)
It can be easily seen that both the problems do not satisfy the hypotheses of Theorem 3.3. To be more precise, (4.4) does not fulfill (v), whereas (4.5) does not verify (iv), having γ > 1. The figures clearly show that the method fails to converge, suggesting us that the assumptions of our main theorem are not too restrictive.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The error sequence {|qr − q* | } r=1,…,100 for problem (4.4).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The error sequence {|qr − q* | } r=1,…,100 for problem (4.5).

Moreover, we point out that, in our experience, some problems arising in the the kinetic theory of dusty plasmas, are more cumbersome than (1.1), and therefore, the application of Newton or other available iterative procedures is not always simple, convenient, or possible. A comparison between FP and other iteration processes on problem of type (1.1) will be the subject of future investigations. Finally, in order to test the performance of our method for larger systems arising from the applications, we discretized a problem of type (1.1) with stepsize h on a sufficiently large interval (0, T), with T = Nh. In this way, we get a nonlinear system of type (1.2), which has dimension N. By applying FP iteration method to such a system for different values of N, with 102 < N < 105, we observe that the number of iterations does not vary with N and so with h, but only with the choice of the starting point q0. Moreover, we underline that in this case the linear systems arising from the FP iterations are tridiagonal and then very easy to be solved.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.