Volume 2012, Issue 1 397250

Research Article

Open Access

Impulsive Synchronization of Multilinks Delayed Coupled Complex Networks with Perturb Effects

Jun Li,

Jun Li

Shiyan Vocational and Technical College, Hubei, Shiyan 442000, China

School of Economics, Huazhong University of Science and Technology, Hubei 430074, China hust.edu.cn

Search for more papers by this author

Bing Li,

Corresponding Author

Bing Li

[email protected]

NOSTA, The Ministry of Science and Technology of China, GPO Box 2143, Beijing 100045, China

Search for more papers by this author

Yuhua Xu,

Corresponding Author

Yuhua Xu

[email protected]

Computer School of Wuhan University, Wuhan 430079, China whu.edu.cn

Department of Mathematics and Finance, Yunyang Teachers′ College, Hubei 442000, China yytc.net.cn

Search for more papers by this author

Wuneng Zhou,

Wuneng Zhou

College of Information Science and Technology, Donghua University, Shanghai 201620, China dhu.edu.cn

Search for more papers by this author

Jian′an Fang,

Jian′an Fang

College of Information Science and Technology, Donghua University, Shanghai 201620, China dhu.edu.cn

Search for more papers by this author

Jun Li,

Jun Li

Shiyan Vocational and Technical College, Hubei, Shiyan 442000, China

School of Economics, Huazhong University of Science and Technology, Hubei 430074, China hust.edu.cn

Search for more papers by this author

Bing Li,

Corresponding Author

Bing Li

[email protected]

NOSTA, The Ministry of Science and Technology of China, GPO Box 2143, Beijing 100045, China

Search for more papers by this author

Yuhua Xu,

Corresponding Author

Yuhua Xu

[email protected]

Computer School of Wuhan University, Wuhan 430079, China whu.edu.cn

Department of Mathematics and Finance, Yunyang Teachers′ College, Hubei 442000, China yytc.net.cn

Search for more papers by this author

Wuneng Zhou,

Wuneng Zhou

College of Information Science and Technology, Donghua University, Shanghai 201620, China dhu.edu.cn

Search for more papers by this author

Jian′an Fang,

Jian′an Fang

College of Information Science and Technology, Donghua University, Shanghai 201620, China dhu.edu.cn

Search for more papers by this author

First published: 13 November 2012

https://doi.org/10.1155/2012/397250

Citations: 1

Academic Editor: Xinzhu Meng

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates impulsive synchronization of multilinks delayed coupled complex networks with perturb effects. Based on the comparison theory of impulsive differential system, a novel synchronization criterion is derived and an impulsive controller is designed simultaneously. Finally, numerical simulations demonstrate the effectiveness of the proposed synchronization criteria.

1. Introduction

In the past few decades, the problem of control and synchronization of complex dynamical networks has been extensively investigated in various fields of science and engineering due to its many potential practical applications [1–8]. One important consideration in practical networks is the existence of time delays because obstructions to the transmission of signals are inevitable in a biological neural network, in an epidemiological model, in a communications network, or in an electrical power grid. Since recently, there are many studies on dynamical networks with time delays [9–16]. Moreover, the multidelayed coupling consists of providing more information about the dynamics in nodes to the other nodes in the network, such as the transportation network; we all know that the transmission speed is different among highway network railway network, and airline network. So we can use timedelay to describe these networks [17]. In [17], the authors studied synchronization of a class of timedelayed complex dynamical networks with multilinks, and this model is suitable to investigate and simulate more realistic complex networks, so we should pay attention to this network with multilinks. Moreover, in [9–11, 17–20], the authors studied synchronization of complex network with time-varying coupling delay by designing a controller and adaptive updated laws. However, the controller designed for such an adaptive synchronization is usually quite complex, it will be useful to find a simple structure to solve this problem, the impulsive controller seems to have a simple structure, and impulsive control is an artificial control strategy which is cheaper to operate compared with other control strategy. Motivated by the above discussions, we investigate impulsive synchronization for such a complex networks model in this paper, and the novel synchronization criterion is derived.

The rest of this work is organized as follows. Section 2 gives the problem formulation. Section 3 gives synchronization scheme. Section 4 gives illustrative example. Section 5 gives the conclusion of the paper.

2. Problem Formulation

In [17], the authors achieve synchronization between two complex networks with multilinks by designing effective controller. For simplicity, the complex network model is written in the following form:

(2.1)

where xⁱ = (x₁, x₂, …, x_n) ^T ∈ Rⁿ, f : Rⁿ → Rⁿ standing for the activity of an individual subsystem is a vector value function.

is the lth subnetwork’s topological structure. The definition of

is that in the lth sub-network, if there exists a link from node i to j (i ≠ j), then

. Otherwise,

is time-delay of the lth subnetwork compared to the zero subnetwork (τ₀ = 0) which is without time delayed.

Remark 2.1. In [17], is defined, we are not concerned whether the coupling matrix A_l satisfies in this paper.

In the paper, we have the following mathematical preliminaries.

Assumption 2.2. We assume that f(xⁱ(t)) is Lipschitz continuous on xⁱ(t), that is, there exists a positive constant η > 0 such that

(2.2)

Assumption 2.3. We also assume that σ(xⁱ(t)) is Lipschitz continuous on xⁱ(t), and one can consider

(2.3)

where ∥M(xⁱ(t), yⁱ(t))∥ ≤ H, H > 0.

3. Synchronization Scheme

In this section, we will investigate impulsive synchronization of the complex networks with perturb functions. The multidelayed coupled complex network with perturb functions can be described by

(3.1)

We take the network given by (3.1) as the driving network and a response network with impulsive control scheme which is given by

(3.2)

(3.3)

where y = (y₁, y₂, …, y_n) ^T ∈ Rⁿ.

Let eⁱ(t) = yⁱ(t) − xⁱ(t), then we have the following error system:

(3.4)

(3.5)

where

Theorem 3.1. Let Assumptions 2.2–2.3 hold, , r = 1,2, …, m. If there exists a constant θ ≥ 1 such that

(3.6)

then the driving network (3.1) and the response network (3.2) can realize impulsive synchronization.

Proof. We choose a nonnegative function as

(3.7)

Then the differentiation of V along the trajectories of (3.4) is

(3.8)

This implies that

(3.9)

On the other hand, when t = t_k, we have

(3.10)

where ρ_k = λ_max[(I + B^ik) ^T(I + B^ik)].

When t ∈ (t₀, t₁], , then

(3.11)

So,

(3.12)

In the same way, for t ∈ (t₁, t₂], we have

(3.13)

In general for any t ∈ (t_k, t_k+1], one finds that

(3.14)

Thus for all t ∈ (t_k, t_k+1], k = 1,2, …, we have

(3.15)

From the assumptions given in the theorem

(3.16)

we have

. That is

When θ ≥ 1, from [21], this implies that the origin in system (3.4) is globally asymptotically stable or the driving network is synchronized with the response network asymptotically for any initial conditions. This completes the proof.

Remark 3.2. Systems (3.1)-(3.2) are the time-invariant complex networks. As discussed in [22–24], systems (3.1)-(3.2) are the time-varying complex networks, which is a more complicated research issue.

Remark 3.3. Normally, it is difficult to control a complex networks by adding the controllers to all nodes, so it would be much better to use the pinning control method since the most complex networks have large number of nodes [25]. Regarding for the pinning control of the network systems (3.1)-(3.2), are the next research topic for us.

Remark 3.4. For the transportation network, we all know that the transmission speed is different among highway network, railway network and airline network. So we can use multilinks delayed to describe these networks [17]. Also impulsive control is an artificial control strategy which is cheaper to operate compared with other control strategy, so impulsive control method of the network systems (3.1)-(3.2) should have potential applications.

4. Illustrative Example

It is well known that the Lorenz system families are typical chaotic systems and the Lü chaotic system is a member of the families which is known as [26]

(4.1)

when a = 36, c = 20, b = 3.

It is well known that the Lü attractor is bounded. Here we suppose that all nodes are running in the given bounded region. Our numerical analyses show that there exist constants M₁ = 25, M₂ = 30, M₃ = 45.

Satisfying ∥y_p∥, ∥z_p∥ ≤ M_p for 1 ≤ p ≤ 3. Therefore, one has

(4.2)

Obviously, ∥P∥ ≈ 52.9843. Thus the Lü system satisfies Assumption 2.2, η = 117.5985. In the same way, it can be seen that the Chen system, the Lorenz system, the unified chaotic system and the Lorenz system families also satisfy Assumption 2.2. So, in the simulations, we select the Lü chaotic system as an example to show the effectiveness of the proposed method [27, 28].

According to Section 3, we show that the network with 4 nodes described by

(4.3)

In numerical simulation, let

(4.4)

we choose τ₁ = 0.1, τ₂ = 0.2, and the gain matrixes B^ik(k = 1,2, …) as a constant matrix, B^ik = B = diag (−0.7, −0.8, −0.9), then ρ_k = 0.09. Let θ = 1.1, from

, then t_k+1 − t_k ≤ 0.0085, we let t_k+1 − t_k = 0.008. All initial values are

. Figure 1 shows the variance of the synchronization errors. We introduce the quantity

[29] which is used to measure the quality of the control process. It is obvious that when E(t) no longer increases, two networks achieve synchronization.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Synchronization errors with time t.

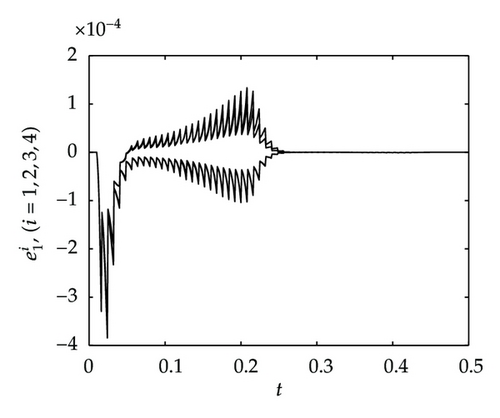
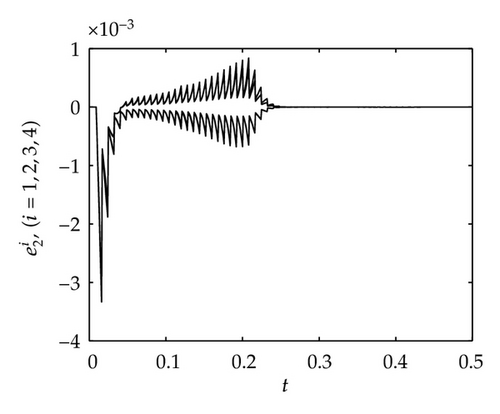
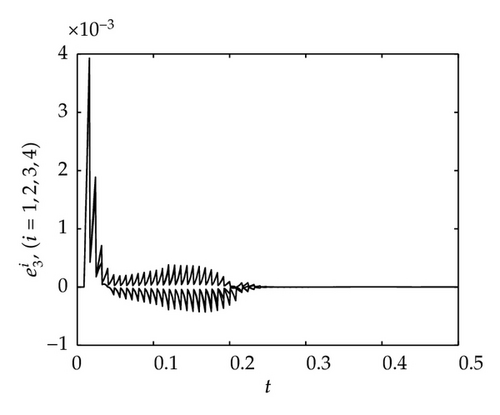
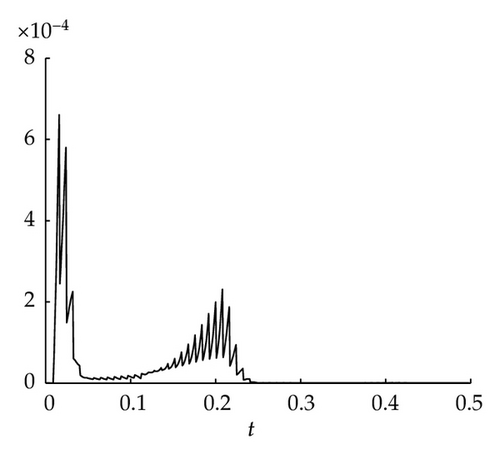
5. Conclusion

This paper deals with the problem of impulsive synchronization of multilinks delayed coupled complex networks with perturb effects. On the basis of the comparison theory of impulsive differential system, the novel synchronization criteriion is derived and an impulsive controller is designed simultaneously. Finally, numerical simulations are presented to verify the effectiveness of the proposed synchronization criteria.

Acknowledgments

The authors would like to thank the referees and the editor for their valuable comments and suggestions. This research is supported by the National Natural Science Foundation of China (61075060), the Science and Technology Research Key Program for the Education Department of Hubei Province of China (D20105001 and D20126002), the Excellent Young Key Talents Cultivation Plan of Hubei Province, China Postdoctoral Science Foundation (2012M511663), the Research Fund for the Technology Development Program of Higher School of Tianjin (20111004), the Social Science Planning Project of Tianjin (TJLJ11-009), and the young talents Fund of Anhui Provinc of China (2011SQRL164).

References

1 Lü J., Yu X., Chen G., and Cheng D., Characterizing the synchronizability of small-world dynamical networks, IEEE Transactions on Circuits and Systems I. (2004) 51, no. 4, 787–796, https://doi.org/10.1109/TCSI.2004.823672, 2066214.
10.1109/TCSI.2004.823672
Web of Science® Google Scholar
2 Li X. and Chen G., Synchronization and desynchronization of complex dynamical networks: an engineering viewpoint, IEEE Transactions on Circuits and Systems I. (2003) 50, no. 11, 1381–1390, https://doi.org/10.1109/TCSI.2003.818611, 2024565.
10.1109/TCSI.2003.818611
Web of Science® Google Scholar
3 Xu Y., Zhou W., Fang J., and Sun W., Adaptive lag synchronization and parameters adaptive lag identification of chaotic systems, Physics Letters A. (2010) 374, no. 34, 3441–3446, 2-s2.0-77955568941, https://doi.org/10.1016/j.physleta.2010.06.064.
10.1016/j.physleta.2010.06.064
CAS Web of Science® Google Scholar
4 Zhou J., Xiang L., and Liu Z., Global synchronization in general complex delayed dynamical networks and its applications, Physica A. (2007) 385, no. 2, 729–742, https://doi.org/10.1016/j.physa.2007.07.006, 2584888.
10.1016/j.physa.2007.07.006
Web of Science® Google Scholar
5 Peng H., Li L., Yang Y., and Sun F., Conditions of parameter identification from time series, Physical Review E. (2011) 83, no. 3, 8, 036202, https://doi.org/10.1103/PhysRevE.83.036202.
10.1103/PhysRevE.83.036202
CAS Web of Science® Google Scholar
6 Shen B., Wang Z., Shu H., and Wei G., On nonlinear H_∞ filtering for discrete-time stochastic systems with missing measurements, IEEE Transactions on Automatic Control. (2008) 53, no. 9, 2170–2180, https://doi.org/10.1109/TAC.2008.930199, 2459593.
10.1109/TAC.2008.930199
Web of Science® Google Scholar
7 Shen B., Wang Z., and Hung Y. S., Distributed H_∞-consensus filtering in sensor networks with multiple missing measurements: the finite-horizon case, Automatica. (2010) 46, no. 10, 1682–1688, https://doi.org/10.1016/j.automatica.2010.06.025, 2877323.
10.1016/j.automatica.2010.06.025
Web of Science® Google Scholar
8 Shen B., Wang Z., Shu H., and Wei G., Robust H_∞ finite-horizon filtering with randomly occurred nonlinearities and quantization effects, Automatica. (2010) 46, no. 11, 1743–1751, https://doi.org/10.1016/j.automatica.2010.06.041, 2878188, ZBL1218.93103.
10.1016/j.automatica.2010.06.041
Web of Science® Google Scholar
9 Xu Y., Zhou W., Fang J., and Lu H., Structure identification and adaptive synchronization of uncertain general complex dynamical networks, Physics Letters A. (2009) 374, no. 2, 272–278, 2-s2.0-71849103324, https://doi.org/10.1016/j.physleta.2009.10.079.
10.1016/j.physleta.2009.10.079
CAS Web of Science® Google Scholar
10 Xu Y., Zhou W., Fang J., and Sun W., Adaptive synchronization of the complex dynamical network with non-derivative and derivative coupling, Physics Letters A. (2010) 374, no. 15-16, 1673–1677, 2-s2.0-77949292101, https://doi.org/10.1016/j.physleta.2010.02.002.
10.1016/j.physleta.2010.02.002
CAS Web of Science® Google Scholar
11 Tang Y., Qiu R., Fang J., Miao Q., and Xia M., Adaptive lag synchronization in unknown stochastic chaotic neural networks with discrete and distributed time-varying delays, Physics Letters A. (2008) 372, no. 24, 4425–4433, https://doi.org/10.1016/j.physleta.2008.04.032, 2432547, ZBL1221.82078.
10.1016/j.physleta.2008.04.032
CAS Web of Science® Google Scholar
12 Zhou J., Xiang L., and Liu Z., Synchronization in complex delayed dynamical networks with impulsive effects, Physica A. (2007) 384, no. 2, 684–692, 2-s2.0-34548051108, https://doi.org/10.1016/j.physa.2007.05.060.
10.1016/j.physa.2007.05.060
Web of Science® Google Scholar
13 Wu X., Synchronization-based topology identification of weighted general complex dynamical networks with time-varying coupling delay, Physica A. (2008) 387, no. 4, 997–1008, 2-s2.0-36649017097, https://doi.org/10.1016/j.physa.2007.10.030.
10.1016/j.physa.2007.10.030
Web of Science® Google Scholar
14 Wu Z.-Y., Li K.-Z., and Fu X.-C., Parameter identification of dynamical networks with community structure and multiple coupling delays, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 11, 3587–3592, https://doi.org/10.1016/j.cnsns.2009.12.028, 2646188, ZBL1222.93058.
10.1016/j.cnsns.2009.12.028
Web of Science® Google Scholar
15 Tang Y., Fang J., Xia M., and Gu X., Synchronization of Takagi-Sugeno fuzzy stochastic discrete-time complex networks with mixed time-varying delays, Applied Mathematical Modelling. (2010) 34, no. 4, 843–855, https://doi.org/10.1016/j.apm.2009.07.015, 2579599, ZBL1185.93145.
10.1016/j.apm.2009.07.015
Web of Science® Google Scholar
16 Xu Y., Zhou W., and Fang J., Topology identification of the modified complex dynamical network with non-delayed and delayed coupling, Nonlinear Dynamics. (2012) 68, no. 1-2, 195–205, https://doi.org/10.1007/s11071-011-0217-x.
10.1007/s11071-011-0217-x
CAS Web of Science® Google Scholar
17 Peng H., Wei N., Li L., Xie W., and Yang Y., Models and synchronization of time-delayed complex dynamical networks with multi-links based on adaptive control, Physics Letters A. (2010) 374, no. 23, 2335–2339, 2-s2.0-77950924376, https://doi.org/10.1016/j.physleta.2010.03.052.
10.1016/j.physleta.2010.03.052
CAS Web of Science® Google Scholar
18 Zhou J., Xiang L., and Liu Z., Synchronization in complex delayed dynamical networks with impulsive effects, Physica A. (2007) 384, no. 2, 684–692, 2-s2.0-34548051108, https://doi.org/10.1016/j.physa.2007.05.060.
10.1016/j.physa.2007.05.060
Web of Science® Google Scholar
19 Li K. and Lai C. H., Adaptive-impulsive synchronization of uncertain complex dynamical networks, Physics Letters A. (2008) 372, no. 10, 1601–1606, https://doi.org/10.1016/j.physleta.2007.10.020, 2396238, ZBL1217.05210.
10.1016/j.physleta.2007.10.020
CAS Web of Science® Google Scholar
20 Cai S., Zhou J., Xiang L., and Liu Z., Robust impulsive synchronization of complex delayed dynamical networks, Physics Letters A. (2008) 372, no. 30, 4990–4995, 2-s2.0-46449094194, https://doi.org/10.1016/j.physleta.2008.05.077.
10.1016/j.physleta.2008.05.077
CAS Web of Science® Google Scholar
21 Yang T., Impulsive Control Theory, 2001, Springer, Berlin, Germany, 1850661.
Web of Science® Google Scholar
22 Lü J. and Chen G., A time-varying complex dynamical network model and its controlled synchronization criteria, IEEE Transactions on Automatic Control. (2005) 50, no. 6, 841–846, https://doi.org/10.1109/TAC.2005.849233, 2142000.
10.1109/TAC.2005.849233
Web of Science® Google Scholar
23 Zhou J., Lü J., and Lu J., Adaptive synchronization of an uncertain complex dynamical network, IEEE Transactions on Automatic Control. (2006) 51, no. 4, 652–656, https://doi.org/10.1109/TAC.2006.872760, 2228029.
10.1109/TAC.2006.872760
Web of Science® Google Scholar
24 Lü J., Yu X., and Chen G., Chaos synchronization of general complex dynamical networks, Physica A. (2004) 334, no. 1-2, 281–302, https://doi.org/10.1016/j.physa.2003.10.052, 2044940.
10.1016/j.physa.2003.10.052
Web of Science® Google Scholar
25 Zhou J., Lü J., and Lu J., Pinning adaptive synchronization of a general complex dynamical network, Automatica. (2008) 44, no. 4, 996–1003, https://doi.org/10.1016/j.automatica.2007.08.016, 2530942.
10.1016/j.automatica.2007.08.016
Web of Science® Google Scholar
26 Lü J. and Chen G., A new chaotic attractor coined, International Journal of Bifurcation and Chaos. (2002) 12, no. 3, 659–661, https://doi.org/10.1142/S0218127402004620, 1894886, ZBL1063.34510.
10.1142/S0218127402004620
Web of Science® Google Scholar
27 Xu Y., Li B., Wang Y., Zhou W., and Fang J., A new four-scroll chaotic attractor consisted of two-scroll transient chaotic and two-scroll ultimate chaotic, Mathematical Problems in Engineering. (2012) 2012, 12, 438328, https://doi.org/10.1155/2012/438328.
10.1155/2012/438328
Web of Science® Google Scholar
28 Xu Y., Zhou W., Fang J., Ma J., and Wang Y., Generating a new chaotic attractor by feedback controlling method, Mathematical Methods in the Applied Sciences. (2011) 34, no. 17, 2159–2166, https://doi.org/10.1002/mma.1513, 2861759, ZBL1230.37111.
10.1002/mma.1513
Web of Science® Google Scholar
29 Lu W., Chen T., and Chen G., Synchronization analysis of linearly coupled systems described by differential equations with a coupling delay, Physica D. (2006) 221, no. 2, 118–134, https://doi.org/10.1016/j.physd.2006.07.020, 2265856, ZBL1111.34056.
10.1016/j.physd.2006.07.020
Web of Science® Google Scholar

Citing Literature

All articles

Impulsive Synchronization of Multilinks Delayed Coupled Complex Networks with Perturb Effects

Abstract

1. Introduction

2. Problem Formulation

3. Synchronization Scheme

4. Illustrative Example

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Impulsive Synchronization of Multilinks Delayed Coupled Complex Networks with Perturb Effects

Abstract

1. Introduction

2. Problem Formulation

3. Synchronization Scheme

4. Illustrative Example

5. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information