Exact Solutions of Generalized Boussinesq-Burgers Equations and (2+1)-Dimensional Davey-Stewartson Equations
Abstract
We study two coupled systems of nonlinear partial differential equations, namely, generalized Boussinesq-Burgers equations and (2+1)-dimensional Davey-Stewartson equations. The Lie symmetry method is utilized to obtain exact solutions of the generalized Boussinesq-Burgers equations. The travelling wave hypothesis approach is used to find exact solutions of the (2+1)-dimensional Davey-Stewartson equations.
1. Introduction
Most nonlinear physical phenomena that appear in many areas of scientific fields such as plasma physics, solid state physics, fluid dynamics, optical fibers, mathematical biology, and chemical kinetics can be modelled by nonlinear partial differential equations (NLPDEs). The investigation of exact travelling wave solutions of these NLPDEs is important for the understanding of most nonlinear physical phenomena and possible applications. To address this issue, various methods for finding travelling wave solutions to NLPDEs have been proposed. Some of the most important methods include homogeneous balance method [1], the ansatz method [2, 3], variable separation approach [4], inverse scattering transform method [5], Bäcklund transformation [6], Darboux transformation [7], Hirota’s bilinear method [8], the (G′/G)-expansion method [9], the reduction mKdV equation method [10], the tri-function method [11, 12], the projective Riccati equation method [13], the sine-cosine method [14, 15], the Jacobi elliptic function expansion method [16, 17], the F-expansion method [18], the exp-function expansion method [19], and Lie symmetry method [20–24].
In this paper, we study two systems of nonlinear partial differential equations, namely, generalized Boussinesq-Burgers equations and (2+1)-dimensional Davey-Stewartson equations. We employ the Lie symmetry method and the travelling wave variable approach to obtain exact solutions to both these systems.
The Lie symmetry approach is one of the most effective methods to determine solutions of nonlinear partial differential equations. Sophus Lie (1842–1899), with the inspiration from Galois’ theory for solving algebraic equations, discovered this method which is known today as Lie group analysis. He showed that many of the known methods of integration of ordinary differential equations could be derived in a systematic manner using his theory of continuous transformation groups. In the past few decades, a considerable amount of development has been made in symmetry methods for differential equations. This is evident by the number of research papers, books, and many new symbolic softwares devoted to the subject [20–24]. The travelling wave variable approach converts the NLPDEs into a nonlinear ordinary differential equations and is often useful in obtaining exact solutions of the partial differential equations.
2. The Generalized Boussinesq-Burgers Equations
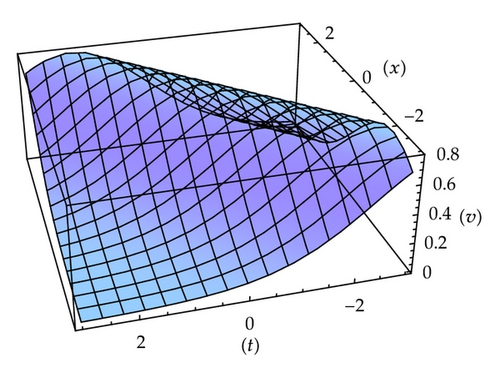
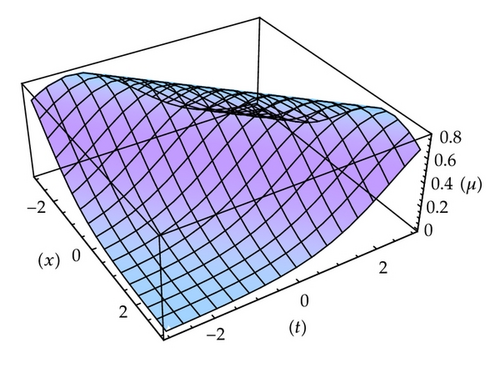
3. The (2+1)-Dimensional Davey-Stewartson Equations
We first transform the (2+1)-dimensional Davey-Stewartson equations (3.1)-(3.2) to a system of nonlinear ordinary differential equations in order to derive its exact solutions.
Now v(x, y, t) can be obtained from (3.6).
It should be noted that the solution (3.12) is valid for 0 < ω < 1 and as ω approaches zero, the solution becomes the normal sine function, sinz, and as ω approaches 1, the solution tends to the tanh function, tanhz.
The profile of the solution (3.12) is given in Figure 2.
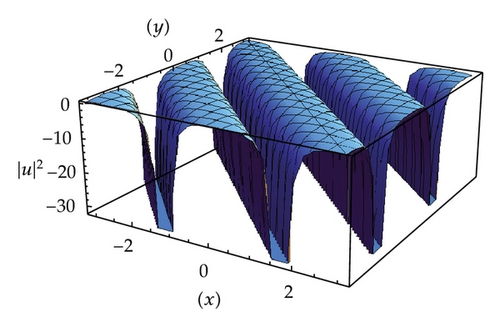
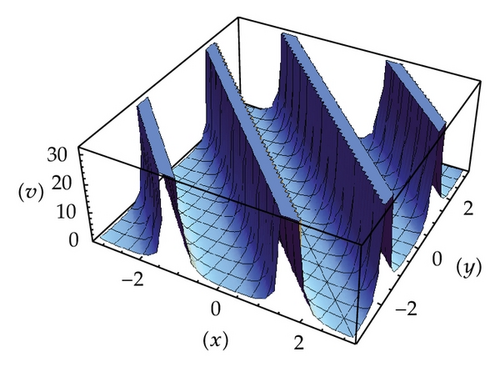
4. Conclusion
In this paper, we studied two systems of nonlinear partial differential equations. Firstly, we obtained exact solutions of the generalized Boussinesq-Burgers equations given by (2.1)-(2.2) using the Lie symmetry method. The solutions obtained were travelling wave solutions. Secondly, we found exact solutions of the (2+1)-dimensional Davey-Stewartson equations (3.1)-(3.2) using the travelling wave hypothesis. The Davey-Stewartson system was first transformed to a system of nonlinear ordinary differential equations, which was then solved to obtain the exact solutions.
Acknowledgments
I. E. Mhlanga and C. M. Khalique would like to thank the Organizing Committee of the Symmetries, Differential Equations, and Applications: Galois Bicentenary Conference (SDEA2012) for their kind hospitality during the conference.




