Multi-State Dependent Impulsive Control for Pest Management
Abstract
According to the integrated pest management strategies, we propose a model for pest control which adopts different control methods at different thresholds. By using differential equation geometry theory and the method of successor functions, we prove the existence of order one periodic solution of such system, and further, the attractiveness of the order one periodic solution by sequence convergence rules and qualitative analysis. Numerical simulations are carried out to illustrate the feasibility of our main results. Our results show that our method used in this paper is more efficient and easier than the existing ones for proving the existence of order one periodic solution.
1. Introduction
2. Preliminaries
First, we give some basic definitions and lemmas.
Definition 2.1. A triple (X, Π, R+) is said to be a semidynamical system if X is a metric space, R+ is the set of all nonnegative real, and Π(P, t) : X × R+ → X is a continuous map such that:
- (i)
Π(P, 0) = P for all P ∈ X;
- (ii)
Π(P, t) is continuous for t and s;
- (iii)
Π(Π(P, t)) = Π(P, t + s) for all P ∈ X and t, s ∈ R+. Sometimes a semi-dynamical system (X, Π, R+) is denoted by (X, Π).
Definition 2.2. Assuming that
- (i)
(X, Π) is a semi-dynamical system;
- (ii)
M is a nonempty subset of X;
- (iii)
function I : M → X is continuous and for any P ∈ M, there exists a ε > 0 such that for any 0<|t | < ε, Π(P, t) ∉ M.
Then, (X, Π, M, I) is called an impulsive semi-dynamical system.
For any P, the function ΠP : R+ → X defined as ΠP(t) = Π(P, t) is continuous, and we call ΠP(t) the trajectory passing through point P. The set C+(P) = {Π(P, t)/0 ≤ t < +∞} is called positive semitrajectory of point P. The set C−(P) = {Π(P, t)/−∞ < t ≤ 0} is called the negative semi-trajectory of point P.
Definition 2.3. One considers state-dependent impulsive differential equations:
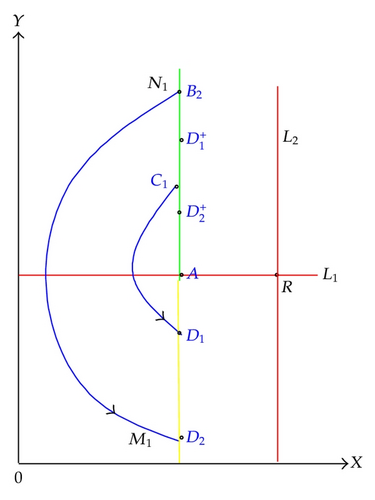
Definition 2.4. Suppose that the impulse set M and the phase set N are both lines, as shown in Figure 1. Define the coordinate in the phase set N as follows: denote the point of intersection Q between N and x-axis as O, then the coordinate of any point A in N is defined as the distance between A and Q and is denoted by yA. Let C denote the point of intersection between the trajectory starting from A and the impulse set M, and let B denote the phase point of C after impulse with coordinate yB. Then, we define B as the successor point of A, and then the successor function of point A is that f(A) = yB − yA.
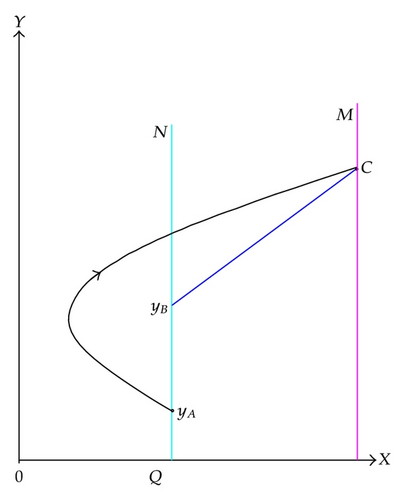
Definition 2.5. A trajectory is called order one periodic solution with period T if there exists a point P0 ∈ N and T > 0 such that P = Π(P0, t) ∈ M and P+ = I(P) = P0.
We get these lemmas from the continuity of composite function and the property of continuous function.
Lemma 2.6. Successor function defined in Definition 2.1 is continuous.
Lemma 2.7. In system (1.4), if there exist A ∈ N, B ∈ N satisfying successor function f(A)f(B) < 0, then there must exist a point P (P ∈ N) satisfying f(P) = 0 the function between the point of A and the point of B, thus there is an order one periodic solution in system (1.4).
Next, we consider the model (1.4) without impulse effects:
- (I)
two steady states O(0,0)-saddle point, and R(d/b(λ − dh), a/b) = R(x*, y*)(λ > dh)-stable centre;
- (II)
a unique closed trajectory through any point in the first quadrant contained inside the point R.
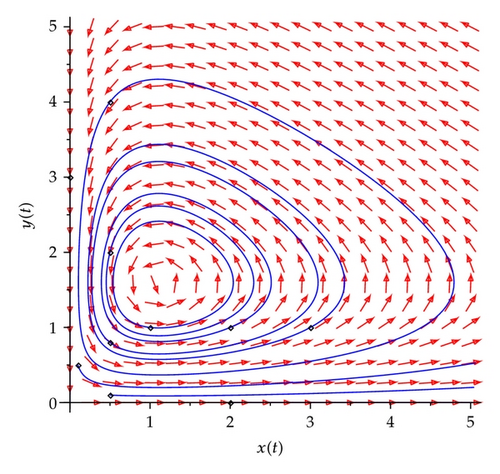
In this paper, we assume that the condition λ > dh holds. By the biological background of system (1.4), we only consider D = {(x, y) : x ≥ 0, y ≥ 0}. Vector graph of system (2.2) can be seen in Figure 2.
This paper is organized as follows. In the next section, we present some basic definitions and an important lemmas as preliminaries. In Section 3, we prove existence for an order one periodic solution of system (1.4). The sufficient conditions for the attractiveness of order one periodic solutions of system (1.4) are obtained in Section 4. At last, we state conclusion, and the main results are carried out to illustrate the feasibility by numerical simulations.
3. Existence of the Periodic Solution
In this section, we will investigate the existence of an order one periodic solution of system (1.4) by using the successor function defined in this paper and qualitative analysis. For this goal, we denote that M1 = {(x, y)/x = h1, 0 ≤ y ≤ a/b}, and that M2 = {(x, y)∣x = h2, y ≥ 0}. Phase set of set M is that N1 = I(M1) = {(x, y)∣x = h1, a/b < y ≤ (a/b) + δ} and that N2 = I(M2) = {(x, y)∣x = (1 − α)h2, y ≥ q}. Isoclinic line is denoted, respectively, by lines: L1 = {(x, y)∣ y = a/b, x ≥ 0} and L2 = {(x, y)∣x = d/b(λ − dh), y ≥ 0}.
For the convenience, if P ∈ Ω − M, F(P) is defined as the first point of intersection of C+(P) and M, that is, there exists a t1 ∈ R+ such that F(P) = Π(P, t1) ∈ M, and for 0 < t < t1, Π(P, t) ∉ M; if B ∈ N, R(B) is defined as the first point of intersection of C−(P) and N, that is, there exists a t2 ∈ R+ such that R(B) = Π(B, −t2) ∈ N, and for −t < t < 0, Π(B, t) ∉ N. For any point P, we denote yP as its ordinate. If the point P(h, yP) ∈ M, then pulse occurs at the point P, the impulsive function transfers the point P into P+ ∈ N. Without loss of generality, unless otherwise specified we assume the initial point of the trajectory lies in phase set N.
Due to the practical significance, in this paper we assume the set always lies in the left side of stable centre R, that is, h1 < d/b(λ − dh) and (1 − α)h2 < d/b(λ − dh).
In the light of the different position of the set N1 and the set N2, we consider the following three cases.
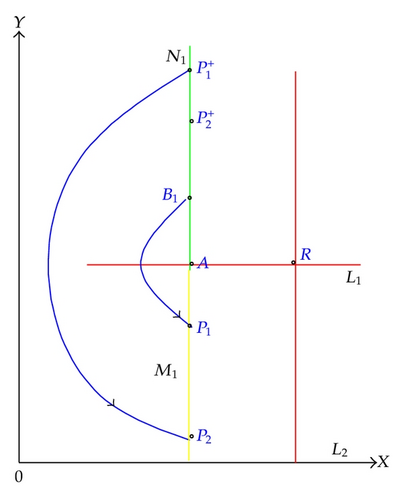
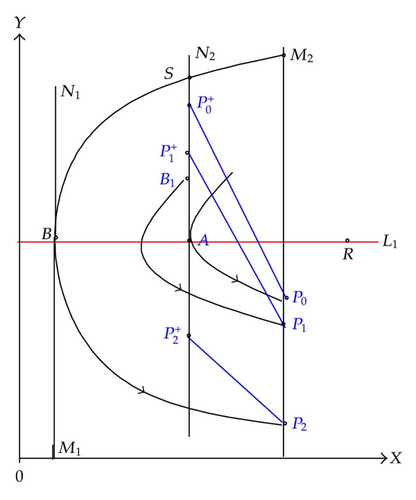
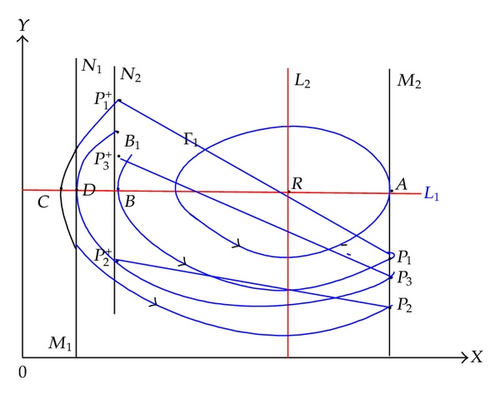
Case 1 (0 < h1 < d/b(λ − dh)). In this case, set M1 and N1 are both in the left side of stable center R (as shown in Figure 3). Take a point B1(h1, (a/b) + ε) ∈ N1 above A, where ε > 0 is small enough, then there must exist a trajectory passing through B1 which intersects with M1 at point , we have . Since p1 ∈ M1, pulse occurs at the point P1, the impulsive function transfers the point P1 into and must lie above B1, therefore inequation holds, thus the successor function of B1 is .
On the other hand, the trajectory with the initial point intersects M1 at point , in view of vector field and disjointness of any two trajectories, we know . Supposing the point P2 is subject to impulsive effects to point , where , the position of has the following two cases.
Subcase 1.1 (). In this case, the point lies above the point A and below , then we have .
By Lemma 2.7, there exists an order one periodic solution of system (1.4), whose initial point is between B1 and in set N1.
Subcase 1.2 ( (as shown in Figure 4)). The point lies below the point A, that is, , then pulse occurs at the point , the impulsive function transfers the point into .
-
If , like the analysis of Subcase 1.1, there exists an order one periodic solution of system (1.4).
-
If , that is, , then we repent the above process until there exists k ∈ Z+ such that jumps to after k times’ impulsive effects which satisfies . Like the analysis of Subcase 1.1, there exists an order one periodic solution of system (1.4).
Now, we can summarize the above results as the following theorem.
Theorem 3.1. If λ > dh, 0 < h1 < d/b(λ − dh), then there exists an order one periodic solution of the system (1.4).
Remark 3.2. It shows from the proved process of Theorem 3.1 that the number of natural enemies should be selected appropriately, which aims to reduce releasing impulsive times to save manpower and resources.
Case 2 (h2 < d/b(λ − dh)). In this case, set M2 and N2 are both in the left side of stable center R, in the light of the different position of the set N2, we consider the following two cases.
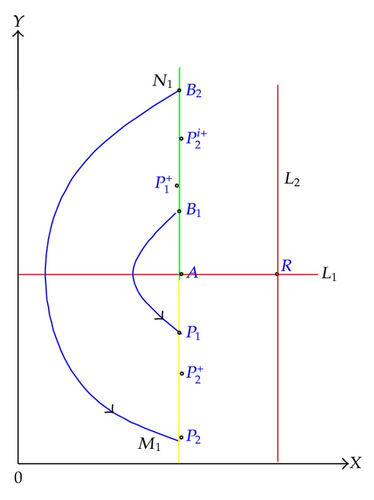
Subcase 2.1 (0 < h1 < (1 − α)h2 < h2 < d/b(λ − dh)). In this case, the set N2 is in the right side of M1 (as shown in Figure 5). The trajectory passing through point A which tangents to N2 at point A intersects with M2 at point . Since the point P0 ∈ M2, then impulse occurs at point P0. Supposing the point P0 is subject to impulsive effects to point , where , the position of has the following three cases:
(1) (). Take a point B1((1 − α)h2, ε + a/b) ∈ N2 above A, where ε > 0 is small enough. Then there must exist a trajectory passing through the point B1 which intersects with the set M2 at point . In view of continuous dependence of the solution on initial value and time, we know and the point P1 is close to P0 enough, so we have the point is close to enough and , then we obtain .
On the other hand, the trajectory passing through point B tangents to N1 at point B. Set . Denote the coordinates of impulsive point corresponding to the point .
-
If then . So we obtain . There exists an order one periodic solution of system (1.4), whose initial point is between the point B1 and the point S in set N2 (Figure 5).
-
If and , we have , we conclude that there exists an order one periodic solution of system (1.4).
-
If and , from the vector field of system (1.4), we know the trajectory of system (1.4) with any initiating point on the N2 will ultimately stay in Ω1 = {(x, y)/0 ≤ x ≤ h1, y ≥ 0} after one impulsive effect. Therefore there is no an order one periodic solution of system (1.4).
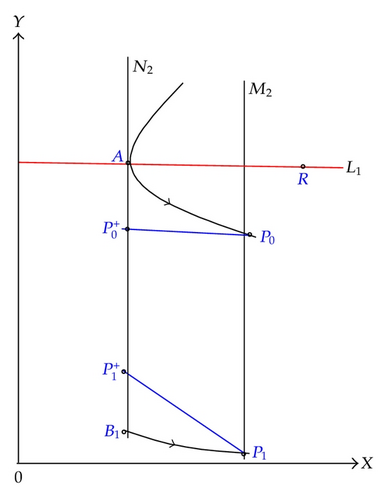
(2) ( (as shown in Figure 6)). In this case, the point lies below the point A, that is, , thus the successor function of the point A is .
Take another point B1((1 − α)h2, ε) ∈ N2, where ε > 0 is small enough. Then there must exist a trajectory passing through the point B1 which intersects M2 at point . Suppose the point is subject to impulsive effects to point , then we have . So we have .
From Lemma 2.7, there exists an order one periodic solution of system (1.4), whose initial point is between B1 and A in set N2.
(3) (). coincides with A, and the successor function of A is that f(A) = 0, so there exists an order one periodic solution of system (1.4) which is just a part of the trajectory passing through the A.
Now, we can summarize the above results as the following theorem.
Theorem 3.3. Assuming that λ > dh and 0 < h1 < (1 − α)h2 < h2 < d/b(λ − dh).
-
If , there exists an order one periodic solutions of the system (1.4).
-
If , if or , and , there exists an order one periodic solutions of the system (1.4).
-
If , and , there is no an order one periodic solutions of the system (1.4). The trajectory of system (1.4) with any initiating point on the N2 will ultimately stay in Ω1 = {(x, y)/0 ≤ x ≤ h1, y ≥ 0} after one impulsive effect.
Subcase 2.2 (0 < (1 − α)h2 < h1 < h2 < d/b(λ − dh)). In this case, the set N2 is on the left side of N1. Any trajectory from initial point will intersect with M1 at some point with time increasing. By the analysis of Case 1, the trajectory from initial point on the set N2 will stay in the region Ω1 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h1}. Similarly, any trajectory from initial point will stay in the region Ω1 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h1} after one impulsive effect or free from impulsive effect.
Theorem 3.4. If λ > dh, 0 < (1 − α)h2 < h1 < h2 < d/b(λ − dh), there is no an order one periodic solutions to the system (1.4), and the trajectory with initial point will stay in the region Ω1 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h1}.
Case 3 (d/b(λ − dh) < h2). In this case, the set M2 is on the right side of stable center R. In the light of the different position of N2, we consider the following two subcases.
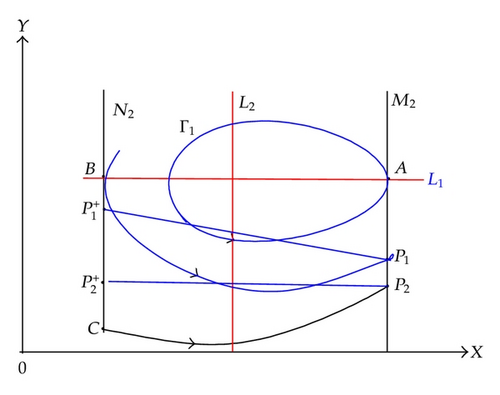
Subcase 3.1 (h1 < (1 − α)h2 < d/b(λ − dh) < h2). In this case, the set M2 is in the right side of R. Then there exists a unique closed trajectory Γ1 of system (1.4) which contains the point R and is tangent to M2 at the point A.
Since Γ1 is closed trajectory, we take their the minimal value δmin of abscissas at the trajectory Γ1, namely, δmin ≤ x holds for any abscissas of Γ1.
(1) (h1 < (1 − α)h2 < δmin < d/b(λ − dh) < h2). In this case, there is a trajectory, which contains the point R(d/b(λ − dh), a/b) and is tangent to the N2 at the point B intersects M2 at a point . Suppose point P1 is subject to impulsive effects to point , here . The position of has the following three sub-cases.
-
If (Figure 7), the point lies below the point B. Like the analysis of Subcase 2.1(2), we can prove there exists an order one periodic solution to the system (1.4) in this case.
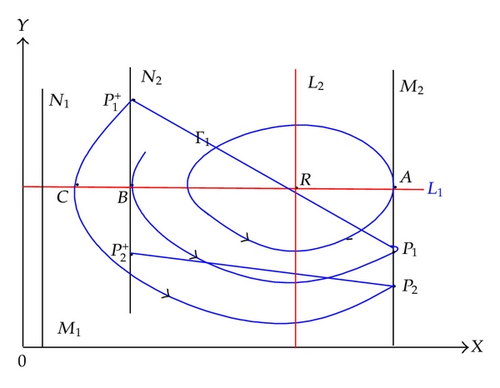
-
If , the point lies above the point B; the trajectory from initiating point intersects with the line L1 at point C. If h1 ≤ yC (Figure 8), we have and , then the successor function of is that . Then, we know that there exists an order one periodic solution of system (1.4), whose initial point is between the point and B in set N2. If h1 > yC (Figure 9), there is a trajectory which is tangent to the N1 at a point D intersects with M2 at a point , P3 jumps to after the impulsive effects. If , we can easily know that there exists an order one periodic solution of system (1.4). If , by the qualitative analysis of the system (1.4), we know that trajectory with any initiating point on the N2 will ultimately stay in Γ1 after a finite number of impulsive effects.
-
If , the point coincides with the point B, and the successor function of the point B is that f(B) = 0; then there exists an order one periodic solution which is just a part of the trajectory passing through the point B.
Now, we can summarize the above results as the following theorem.
Theorem 3.5. Assuming that λ > dh and h1 < (1 − α)h2 < δmin < d/b(λ − dh) < h2.
-
If , there exists an order one periodic solution to the system (1.4).
-
If and h1 ≤ yC, then there exists an order one periodic solution to the system (1.4).
-
If , h1 > yC and , then there exists an order one periodic solution to the system (1.4).
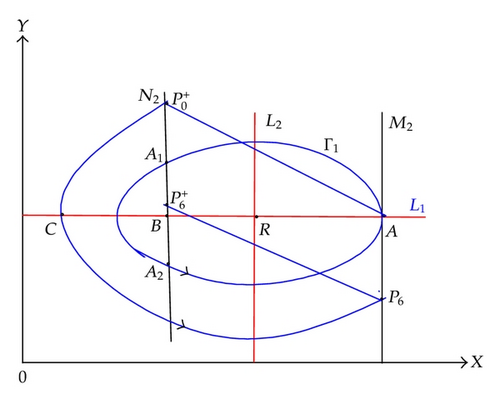
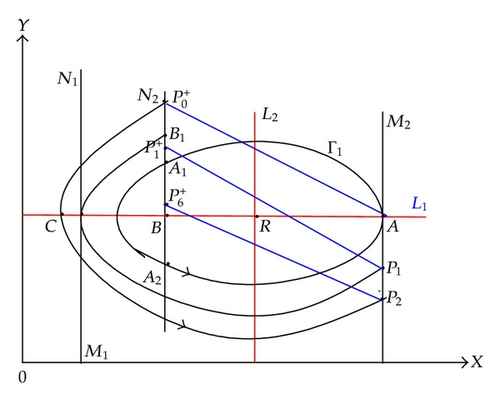
(2) (h1 < δmin < (1 − α)h2 < d/b(λ − dh) < h2). In this case, denote the closed trajectory Γ1 of system (1.4) intersects with N2 two points and (as shown in Figure 10). Since A ∈ M2, impulse occurs at the point A. Suppose point A is subject to impulsive effects to point , here .
-
If or , then coincides with A1 or coincides with A2, and the successor function of A1 or A2 is that f(A1) = 0 or f(A2) = 0. So, there exists an order one periodic solution of system (1.4) which is just a part of the trajectory Γ1.
-
If , the point lies below the point A2. Like the analysis of Subcase 2.1(2), we can prove there exists an order one periodic solution to the system (1.4) in this case.
-
If (as shown in Figure 11), the point is above the point A1. Like the analysis of Subcase 3.1(1), we obtain sufficient conditions of existence of order one periodic solution to the system (1.4).
Theorem 3.6. Assuming that λ > dh, h1 < (1 − α)h2 < δmin < d/b(λ − dh) < h2.
-
If , there exists an order one periodic solution to the system (1.4).
-
If and h1 ≤ yC, then there exists an order one periodic solution to the system (1.4).
-
If , and , then there exists an order one periodic solution to the system (1.4).
(3) (). In this case, we note that the point must lie between the point A1 and the point A2 (As shown in Figure 12). Taking a point B1 ∈ M2 such that B1 jumps to A2 after the impulsive effect, denote . Since , we have . Let , take a point B2 ∈ M2 such that B2 jumps to after the impulsive effects, then we have , . This process continues until there exists a (K ∈ Z+) satisfying . So we obtain a sequence of the set M2 and a sequence {Bk} k=1,2,…,K of set N2 satisfying . In the following, we will prove the trajectory of system (1.4) with any initiating point of set N2 will ultimately stay in Γ1.
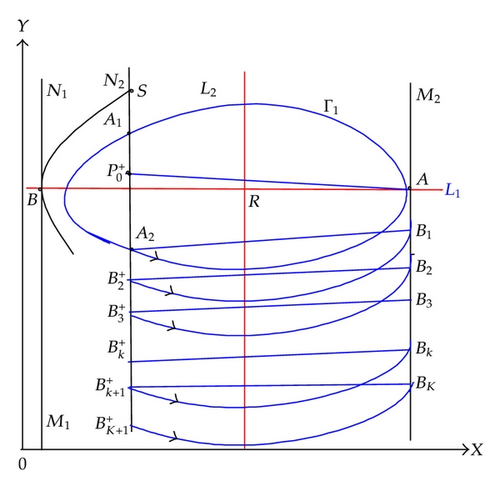
From the vector field of system (1.4), we know the trajectory of system (1.4) with any initiating point between the point A1 and A2 will be free from impulsive effect and ultimately will stay in Γ1.
For any point below A2, it must lie between and , here k = 2,3, …, K + 1 and . After k times’ impulsive effects, the trajectory with this initiating point will arrive at some point of the set N2 which must be between A1 and A2, and then ultimately stay in Γ1.
Denote the intersection of the trajectory passing through the point B which tangents to N1 at point B with the set N2 at S((1 − α)h2, yS). With time increasing, the trajectory of system (1.4) from any initiating point on segment intersect with the set N2 at some point which is below A2; so just like the analysis above we obtain, it will ultimately stay in Γ1. So for any point below S, will ultimately stay in region Γ1 with time increasing.
Now, we can summarize the above results as the following theorem.
Theorem 3.7. Assuming that λ > dh, h1 < δmin < (1 − α)h2 < d/b(λ − dh) < h2, and , there is no periodic solution in system (1.4), and the trajectory with any initiating point on the set N2 will stay in Γ1 or in the region Ω1 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h1}.
Subcase 3.2 (0 < (1 − α)h2 < h1 < d/b(λ − dh) < h2). In this case, the set N2 is on the left side of the set N1 and M2 in the right side of R. Like the analysis of Subcase 2.2, we can know that any trajectory with initial point will stay in the region Ω1 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h1} after one impulsive effect or free from impulsive effect.
4. Attractiveness of the Order One Periodic Solution
In this section, under the condition of existence of order one periodic solution to system (1.4) and the initial value of pest population x(0) ≤ h2, we discuss its attractiveness. We focus on Case 1 and Case 2; by similar method, we can obtain similar results about Case 3.
Theorem 4.1. Assuming that λ > dh, h1 < d/(b(λ − dh)) and δ ≥ a/b.
If or (Figure 14), then
Proof. By the derivation of Theorem 3.1, we know there exists an order one periodic solution of system (1.4). We assume trajectory and segment formulate an order one periodic solution of system (1.4), that is, there exists a P+ ∈ N2 such that the successor function of P+ satisfies f(P+) = 0. First, we will prove the uniqueness of the order one periodic solution.
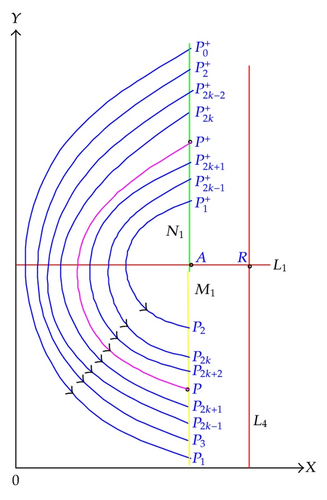
We take any two points satisfying , then we obtain two trajectories whose initiate points are C1 and C2 intersects the set M1 two points and , respectively, (Figure 13). In view of the vector field of system (1.4) and the disjointness of any two trajectories without impulse, we know . Suppose the points D1 and D2 are subject to impulsive effect to points and , respectively, then we have and , so we get f(C1) − f(C2) < 0, thus we obtain the successor function f(x) is decreasing monotonously of N1, so there is a unique point P+ ∈ N1 satisfying f(P+) = 0, and the trajectory is a unique order one periodic solution of system (1.4).
Next, we prove the attractiveness of the order one periodic solution in the region Ω0 = {(x, y)∣x ≥ 0, y ≥ 0, x ≤ h2}. We focus on the case ; by similar method, we can obtain similar results about case (Figure 14).
Take any point above P+. Denote the first intersection point of the trajectory from initiating point with the set M1 at , and the corresponding consecutive points are , respectively. Consequently, under the effect of impulsive function, the corresponding points after pulse are .
Due to conditions , , δ ≥ a/b and disjointness of any two trajectories, then we get a sequence of the set N1 satisfying
So the successor function and hold. Series increases monotonously and has upper bound, so exists. Next, we will prove . Set lim k→∞ P2k−1 = C+, we will prove P+ = C+. Otherwise P+ ≠ C+, then there is a trajectory passing through the point C+ which intersects the set M1 at point , then we have , . Since f(C+) ≥ 0 and P+ ≠ C+, according to the uniqueness of the periodic solution, then we have , thus hold. Analogously, let trajectory passing through the point C+ which intersects the set M1 at point , and the corresponding consecutive points is , then , then we have , this is, contradict to the fact that C+ is a limit of sequence , so we obtain P+ = C+. So, we obtain . Similarly, we can prove .
From above analysis, we know there exists a unique order one periodic solution in system (1.4), and the trajectory from initiating any point of the N1 will ultimately tend to be order one periodic solution .
Any trajectory from initial point will intersect with N1 at some point with time increasing on the condition that (1 − α)h2 < h1 < h2 < d/b(λ − dh); therefore the trajectory from initial point on N1 ultimately tends to be order one periodic solution . Therefore, order one periodic solution is attractive in the region Ω0. This completes the proof.
Remark 4.2. Assuming that λ > dh, h1 < h2 < d/b(λ − dh) and δ ≥ a/b, if or then the order one periodic solution is unattractive.
Theorem 4.3. Assuming that λ > dh, h1 < (1 − α)h2 < h2 < d/b(λ − dh) and (as shown in Figure 15), then
- (I)
There exists an odd number of order one periodic solutions of system (1.4) with initial value between and A in set N2.
- (II)
If the periodic solution is unique, then the periodic solution is attractive in region Ω2, here Ω2 is open region which is constituted by trajectory , segment , segment , and segment .
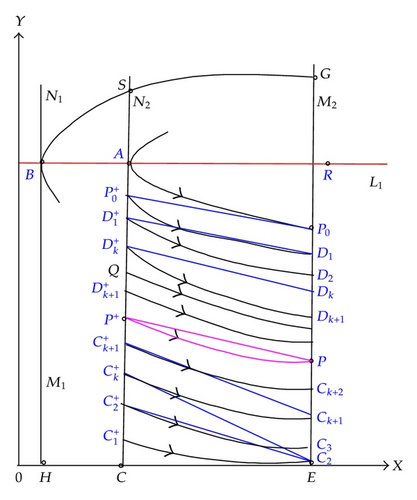
Proof. (I) According to the Subcase 2.1(2), f(A) < 0 and , and the continuous successor function f(x), there exists an odd number of root satisfying f(x) = 0, then we can get there exists an odd number of order one periodic solutions of system (1.4) with initial value between and A in set N2.
(II) By the derivation of Theorem 3.3, we know there exists an order one periodic solution of system (1.4) whose initial point is between and in the set N2. Assume trajectory and segment formulate the unique order one periodic solution of system (1.4) with initial point P+ ∈ N2.
On the one hand, take a point satisfying and . The trajectory passing through the point which intersects with the set M2 at point , that is, , then we have , thus , since . So, we obtain ; Set , because , we know , then we have and . This process is continuing, then we get a sequence of the set N2 satisfying
On the other hand, set , then D1 jumps to under the impulsive effects. Since , we have , thus we obtain . Set , then D2 jumps to under the impulsive effects. We have ; this process is continuing, we can obtain a sequence of the set N2 satisfying
Any point Q ∈ N2 below A must be in some interval , , , . Without loss of generality, we assume the point . The trajectory with initiating point Q moves between trajectory and and intersects with M2 at some point between Dk+2 and Dk+1; under the impulsive effects, it jumps to the point of N2 which is between , then trajectory continues to move between trajectory and . This process can be continued unlimitedly. Since , the intersection sequence of trajectory , and the set N2 will ultimately tend to the point P+. Similarly, if , we also can get the intersection sequence of trajectory and the set N2 will ultimately tend to point P+. Thus, the trajectory initiating any point below A ultimately tend to the unique order one periodic solution .
Denote the intersection of the trajectory passing through the point B which tangents to N1 at the point B with the set N2 at a point S((1 − α)h2, yS). The trajectory from any initiating point on segment will intersect with the set N2 at some point below A with time increasing. So like the analysis above, we obtain the trajectory from any initiating point on segment will ultimately tend to be the unique order one periodic solution .
Since the trajectory with any initiating point of the Ω2 will certainly intersect with the set N2, then from the above analysis, we know the trajectory with any initiating point on segment will ultimately tend to be order one periodic solution . Therefore, the unique order one periodic solution is attractive in the region Ω2. This completes the proof.
Remark 4.4. Assuming that λ > dh, h1 < (1 − α)h2 < h2 < d/b(λ − dh), and , then the order one periodic solution with initial point between A and is unattractive.
Theorem 4.5. Assuming that λ > dh, h1 < (1 − α)h2 < h2 < d/b(λ − dh), (Figure 16) then, there exists a unique order one periodic solution of system (1.4) which is attractive in the region Ω2, here Ω2 is open region which enclosed by trajectory , segment , segment and segment .
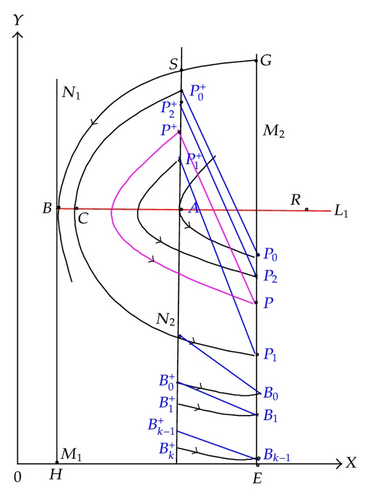
Proof. By the derivation of Theorem 3.3, we know there exists an order one periodic solution of system (1.4). We assume trajectory and segment formulate an order one periodic solution of system (1.4), that is, P+ ∈ N2 is its initial point satisfying f(P+) = 0. Like the proof of Theorem 4.1, we can prove the uniqueness of the order one periodic solution of system (1.4).
Next, we prove the attractiveness of the order one periodic solution in the region Ω2.
Denote the first intersection point of the trajectory from initiating point with the impulsive set M2 at , and the corresponding consecutive points are respectively. Consequently, under the effect of impulsive function I, the corresponding points after pulse are , …. In view of and disjointness of any two trajectories, we have
The trajectory from initiating point between and will intersect with impulsive set N2 with time increasing, under the impulsive effects it arrives at a point of N2 which is between or . Then like the analysis of Theorem 4.3, we know the trajectory from any initiating point between and will ultimately tend to be order one periodic solution .
Denote the intersection of the trajectory passing through point B which tangents to N1 at point B with the set N2 at S. Since the trajectory from initiating any point below S of the set N2 will certain intersect with set N2, next we only need to prove the trajectory with any initiating point below S of the set N2 will ultimately tend to be order one periodic solution .
Assume a point B0 of set M2 jumps to under the impulsive effect. Set . Assume point B1 of set N2 jumps to under the impulsive effect. Set . This process is continuing until there exists a () satisfying . So we obtain a sequence of set M2 and a sequence of set N2 satisfying . For any point of set N2 below , it must lie between and here k = 1,2, …, K0. After K0 + 1 times’ impulsive effects, the trajectory with this initiating point will arrive at some point of the set N2 which must be between and , and then will ultimately tend to order one periodic solution . There is no order one periodic solution with the initial point below .
The trajectory with any initiating point in segment will intersect with the set N2 at some point below with time increasing. Like the analysis above, we obtain the trajectory initiating any point on segment will ultimately tend to be the unique order one periodic solution .
From above analysis, we know there exists a unique order one periodic solution in system (1.4), and the trajectory from any initiating point below S will ultimately tend to be order one periodic solution . Therefore, order one periodic solution is attractive in the region Ω2. This completes the proof.
5. Conclusion
In this paper, a state-dependent impulsive dynamical model concerning different control methods at different thresholds is proposed, we find a new method to study existence and attractiveness of order one periodic solution of such system. We define semicontinuous dynamical system and successor function, demonstrate the sufficient conditions that system (1.4) exists order one periodic solution with differential geometry theory and successor function. Besides, we successfully prove the attractiveness of the order one periodic solution by sequence convergence rules and qualitative analysis.The method can be also extended to mechanical dynamical systems with impacts, for example [19, 20].
These results show that the state-dependent impulsive effects contribute significantly to the richness of the dynamics of the model. The conditions of existence of order one periodic solution in this paper have more extensively applicable scope than the conditions given in [14]. Our results show that, in theory, a pest can be controlled such that its population size is no larger than its ET by applying effects impulsively once, twice, or at most, a finite number of times, or according to a periodic regime. The methods of the theorems are proved to be new in this paper, and these methods are more efficient and easier to operate than the existing research methods which have been applied the models with impulsive state feedback control [16–18, 21], so they are deserved further promotion. In this paper, according to the integrated pest management strategies, we propose a model for pest control which adopts different control methods at different thresholds, the corresponding control is exerted, which leads to the two state impulses in model. Certainly, many biological systems will always be described by three or more state variables, which are the main work in the future.
Example 5.1. Existence and attractiveness of order one periodic solution.
We set h1 = 1, α = 0.6, β = 0.8, q = 0.8, h2 = 1.8, initiating points are (0.85,0.2) (red), (0.8,0.5) (green), and (0.75,0.11) (blue), respectively. Figure 17 shows that the conditions of Theorems 3.1 and 4.1 hold, system (5.1) exists order one periodic solution. The trajectory from different initiating must ultimately tend to be the order one periodic solution. Therefore, order one periodic solution is attractive.
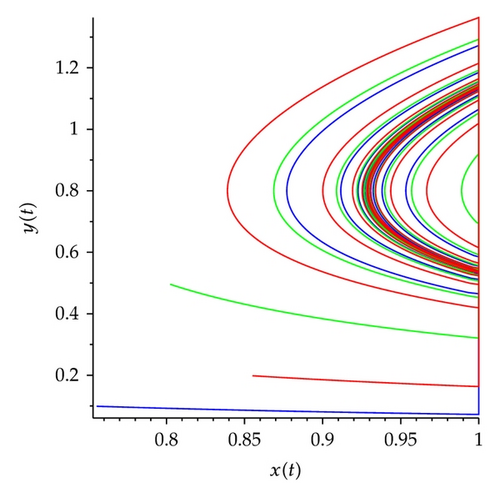
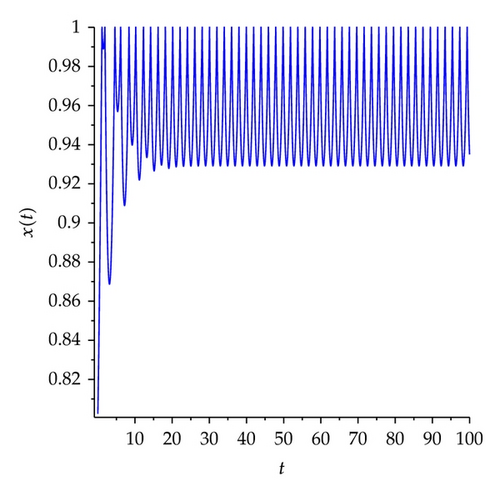
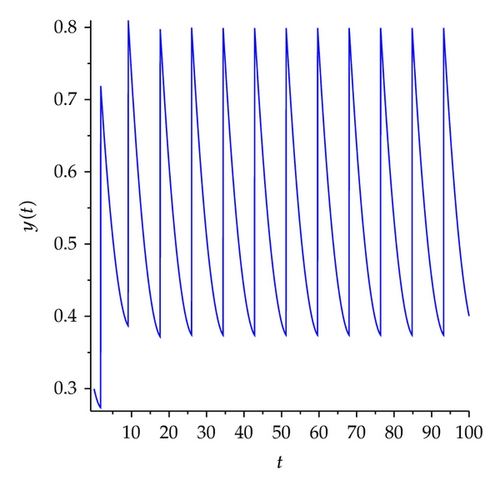
Example 5.2. Existence and attractiveness of positive periodic solution.
We set h1 = 0.7, α = 0.6, β = 0.8, q = 0.8, h2 = 1.8, h1 < (1 − α)h2 < x*, initiating points are (0.8,0.1) (red), (0.7,0.5) (green), and (0.75,0.3) (blue), respectively. Figure 18 shows that the conditions of Theorems 3.3 and 4.3 hold, there exists order one periodic solution of the system (5.1), and the trajectory from different initiating must ultimately tend to be the order one periodic solution. Therefore, order one periodic solution is attractive.
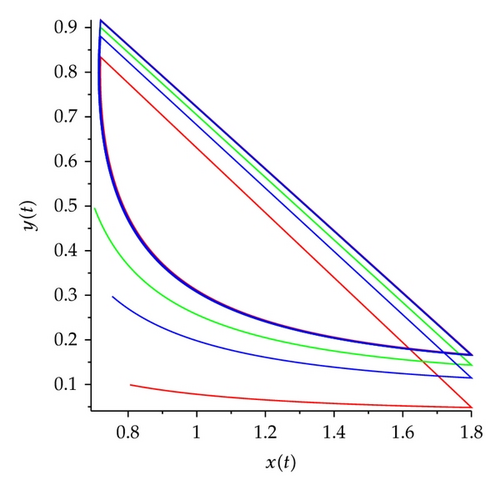
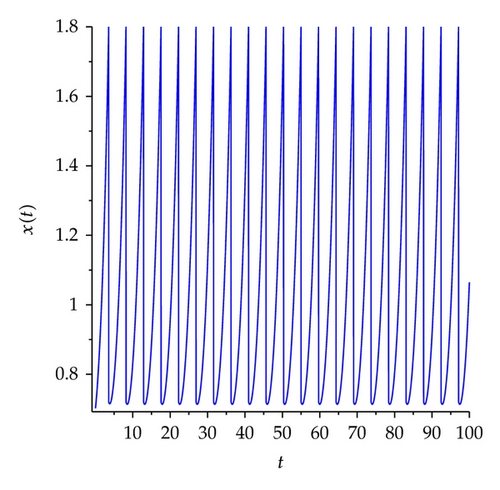
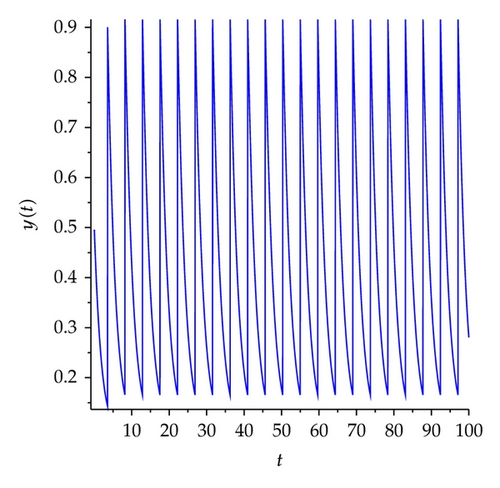
Example 5.3. Existence and attractive of positive periodic solutions.
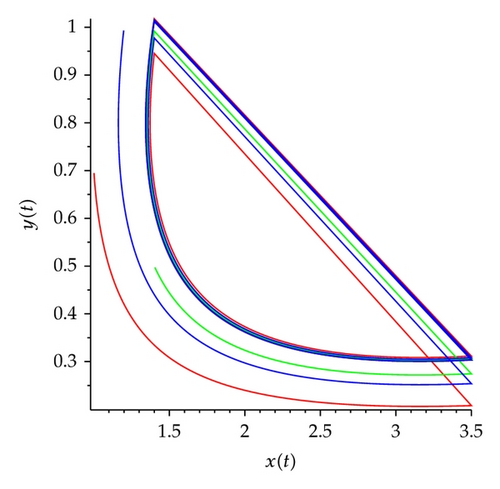
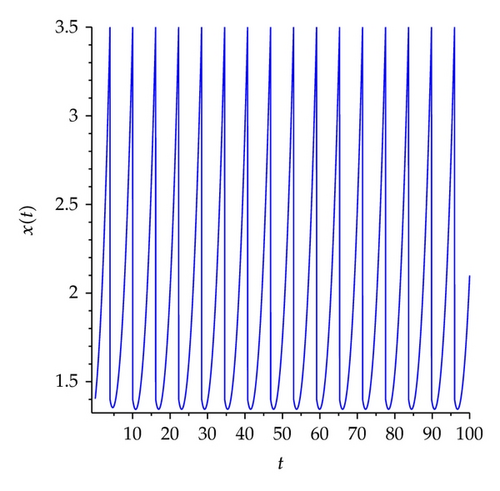
We set h1 = 0.7, α = 0.6, β = 0.8, q = 0.8, h2 = 3.5, h1 < (1 − α)h2 < x* < h2, initiating points are (1,0.7) (red), (1.4,0.5) (green), and (1.2,1) (blue) as shown in Figure 19. Therefore, the conditions of Theorems 3.6 and 4.5 hold, then system (5.1) exists order one periodic solution, and it is attractive.
Acknowledgment
This Project supported by the National Natural Science Foundation of China (no. 10872118).




