Volume 2012, Issue 1 381069

Research Article

Open Access

Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p, (1 < p < ∞)

Corresponding Author

Ali Karaisa

[email protected]

Department of Mathematics, Faculty of Sciences, Konya Necmettin Erbakan University, Karacian Mahallesi, Ankara Caddesi 74, 42060 Konya, Turkey konya.edu.tr

Search for more papers by this author

Ali Karaisa,

Corresponding Author

Ali Karaisa

[email protected]

Department of Mathematics, Faculty of Sciences, Konya Necmettin Erbakan University, Karacian Mahallesi, Ankara Caddesi 74, 42060 Konya, Turkey konya.edu.tr

Search for more papers by this author

First published: 26 September 2012

https://doi.org/10.1155/2012/381069

Citations: 7

Academic Editor: Antonia Vecchio

Share a link

Email
Wechat
Bluesky

Abstract

The operator on sequence space on ℓ_p is defined , where x = (x_k) ∈ ℓ_p, and and are two convergent sequences of nonzero real numbers satisfying certain conditions, where (1 < p < ∞). The main purpose of this paper is to determine the fine spectrum with respect to the Goldberg′s classification of the operator defined by a double sequential band matrix over the sequence space ℓ_p. Additionally, we give the approximate point spectrum, defect spectrum, and compression spectrum of the matrix operator over the space ℓ_p.

1. Introduction

Let X and Y be Banach spaces, and let T : X → Y also be a bounded linear operator. By R(T), we denote the range of T, that is,

(1.1)

By B(X), we also denote the set of all bounded linear operators on X into itself. If X is any Banach space and T ∈ B(X), then the adjoint T^* of T is a bounded linear operator on the dual X^* of X defined by (T^*f)(x) = f(Tx) for all f ∈ X^* and x ∈ X.

Given an operator T ∈ B(X), the set

(1.2)

is called the resolvent set of T and its complement with respect to the complex plain

(1.3)

is called the spectrum of T. By the closed graph theorem, the inverse operator

(1.4)

is always bounded and is usually called resolvent operator of T at λ.

2. Subdivisions of the Spectrum

In this section, we give the definitions of the parts point spectrum, continuous spectrum, residual spectrum, approximate point spectrum, defect spectrum, and compression spectrum of the spectrum. There are many different ways to subdivide the spectrum of a bounded linear operator. Some of them are motivated by applications to physics, in particular, quantum mechanics.

2.1. The Point Spectrum, Continuous Spectrum, and Residual Spectrum

The name resolvent is appropriate, since helps to solve the equation T_λx = y. Thus, provided exists. More important, the investigation of properties of will be basic for an understanding of the operator T itself. Naturally, many properties of T_λ and depend on λ, and spectral theory is concerned with those properties. For instance, we will be interested in the set of all λ′s in the complex plane such that exists. Boundedness of is another property that will be essential. We will also ask for what λ′s the domain of is dense in X, to name just a few aspects. A regular value λ of T is a complex number such that exists and bounded and whose domain is dense in X. For our investigation of T, T_λ, and , we need some basic concepts in spectral theory, which are given as follows (see [1, pp. 370-371]).

The resolvent set ρ(T, X) of T is the set of all regular values λ of T. Furthermore, the spectrum σ(T, X) is partitioned into three disjoint sets as follows.

The point (discrete) spectrum σ_p(T, X) is the set such that does not exist. An λ ∈ σ_p(T, X) is called an eigenvalue of T.

The continuous spectrum σ_c(T, X) is the set such that exists and is unbounded and the domain of is dense in X.

The residual spectrum σ_r(T, X) is the set such that exists (and may be bounded or not), but the domain of is not dense in X.

Therefore, these three subspectra form a disjoint subdivisions

(2.1)

To avoid trivial misunderstandings, let us say that some of the sets defined above, may be empty. This is an existence problem, which we will have to discuss. Indeed, it is well known that σ_c(T, X) = σ_r(T, X) = ∅ and the spectrum σ(T, X) consists of only the set σ_p(T, X) in the finite-dimensional case.

2.2. The Approximate Point Spectrum, Defect Spectrum, and Compression Spectrum

In this subsection, following Appell et al. [2], we define the three more subdivisions of the spectrum called as the approximate point spectrum, defect spectrum, and compression spectrum.

Given a bounded linear operator T in a Banach space X, we call a sequence (x_k) in X as a Weyl sequence for T if ∥x_k∥ = 1 and ∥Tx_k∥ → 0, as k → ∞.

In what follows, we call the set

(2.2)

the approximate point spectrum of T. Moreover, the subspectrum

(2.3)

is called defect spectrum of T.

The two subspectra given by (2.2) and (2.3) form a (not necessarily disjoint) subdivision

(2.4)

of the spectrum. There is another subspectrum

(2.5)

which is often called compression spectrum in the literature. The compression spectrum gives rise to another (not necessarily disjoint) decomposition

(2.6)

of the spectrum. Clearly, σ_p(T, X)⊆σ_ap(T, X) and σ_co(T, X)⊆σ_δ(T, X). Moreover, comparing these subspectra with those in (2.1) we note that

(2.7)

Sometimes it is useful to relate the spectrum of a bounded linear operator to that of its adjoint. Building on classical existence and uniqueness results for linear operator equations in Banach spaces and their adjoints is also useful.

Proposition 2.1 (see [2], Proposition 1.3, p. 28.)Spectra and subspectra of an operator T ∈ B(X) and its adjoint T^* ∈ B(X^*) are related by the following relations:

(a)
σ(T^*, X^*) = σ(T, X),
(b)
σ_c(T^*, X^*)⊆σ_ap(T, X),
(c)
σ_ap(T^*, X^*) = σ_δ(T, X),
(d)
σ_δ(T^*, X^*) = σ_ap(T, X),
(e)
σ_p(T^*, X^*) = σ_co(T, X),
(f)
σ_co(T^*, X^*)⊇σ_p(T, X),
(g)
σ(T, X) = σ_ap(T, X) ∪ σ_p(T^*, X^*) = σ_p(T, X) ∪ σ_ap(T^*, X^*).

The relations (c)–(f) show that the approximate point spectrum is in a certain sense dual to defect spectrum, and the point spectrum dual to the compression spectrum.

The equality (g) implies, in particular, that σ(T, X) = σ_ap(T, X) if X is a Hilbert space and T is normal. Roughly speaking, this shows that normal (in particular, self-adjoint) operators on Hilbert spaces are most similar to matrices in finite-dimensional spaces (see [2]).

2.3. Goldberg′s Classification of Spectrum

If X is a Banach space and T ∈ B(X), then there are three possibilities for R(T):

(A)
R(T) = X,
(B)
,
(C)
,

and

(1)
T⁻¹ exists and is continuous,
(2)
T⁻¹ exists but is discontinuous,
(3)
T⁻¹ does not exist.

If these possibilities are combined in all possible ways, nine different states are created. These are labelled by: A₁, A₂, A₃, B₁, B₂, B₃, C₁, C₂, C₃. If an operator is in state C₂, for example, then and T⁻¹ exist but is discontinuous (see [3] and Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State diagram for B(X) and B(X^*) for a nonreflective Banach space X.

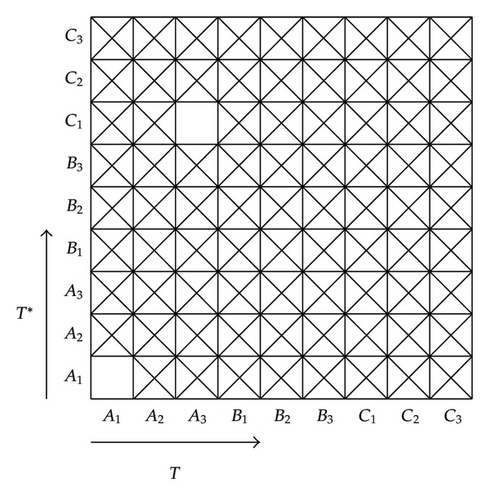
If λ is a complex number such that T_λ = λI − T ∈ A₁ or T_λ = λI − T ∈ B₁, then λ ∈ ρ(T, X). All scalar values of λ not in ρ(T, X) comprise the spectrum of T. The further classification of σ(T, X) gives rise to the fine spectrum of T. That is, σ(T, X) can be divided into the subsets A₂σ(T, X) = ∅, A₃σ(T, X), B₂σ(T, X), B₃σ(T, X), C₁σ(T, X), C₂σ(T, X), and C₃σ(T, X). For example, if T_λ = λI − T is in a given state, C₂ (say), then we write λ ∈ C₂σ(T, X).

By the definitions given above, we can illustrate the subdivisions (2.1) in Table 1.

Table 1. Subdivisions of spectrum of a linear operator.

		exists and is bounded	exists and is unbounded	does not exist
		1	2	3
A	R(λI − T) = X	λ ∈ ρ(T, X)	—	λ ∈ σ_p(T, X)
A	R(λI − T) = X	λ ∈ ρ(T, X)	—	λ ∈ σ_ap(T, X)

			λ ∈ σ_c(T, X)	λ ∈ σ_p(T, X)
B		λ ∈ ρ(T, X)	λ ∈ σ_ap(T, X)	λ ∈ σ_ap(T, X)
			λ ∈ σ_δ(T, X)	λ ∈ σ_δ(T, X)

		λ ∈ σ_r(T, X)	λ ∈ σ_r(T, X)	λ ∈ σ_p(T, X)
C		λ ∈ σ_δ(T, X)	λ ∈ σ_ap(T, X)	λ ∈ σ_ap(T, X)
C		λ ∈ σ_δ(T, X)	λ ∈ σ_δ(T, X)	λ ∈ σ_δ(T, X)
		λ ∈ σ_co(T, X)	λ ∈ σ_co(T, X)	λ ∈ σ_co(T, X)

Observe that the case in the first row and second column cannot occur in a Banach space X, by the closed graph theorem. If we are not in the third column, that is, if λ is not an eigenvalue of T, we may always consider the resolvent operator (on a possibly “thin” domain of definition) as “algebraic” inverse of λI − T.

By a sequence space, we understand a linear subspace of the space of all complex sequences which contains ϕ, the set of all finitely nonzero sequences, where ℕ₁ denotes the set of positive integers. We write ℓ_∞, c, c₀, and bv for the spaces of all bounded, convergent, null, and bounded variation sequences, which are the Banach spaces with the sup-norm ∥x∥_∞ = sup _k∈ℕ | x_k| and , while ϕ is not a Banach space with respect to any norm, respectively, where ℕ = {0,1, 2, …}. Also by ℓ_p, we denote the space of all p-absolutely summable sequences, which is a Banach space with the norm , where 1 ⩽ p < ∞.

Let A = (a_nk) be an infinite matrix of complex numbers a_nk, where n, k ∈ ℕ, and write

(2.8)

where D₀₀(A) denotes the subspace of w consisting of x ∈ w for which the sum exists as a finite sum. For simplicity in notation, here and in what follows, the summation without limits runs from 0 to ∞, and we will use the convention that any term with negative subscript is equal to naught. More generally if μ is a normed sequence space, we can write D_μ(A) for the x ∈ w for which the sum in (2.8) converges in the norm of μ. We write

(2.9)

for the space of those matrices which send the whole of the sequence space λ into μ in this sense.

We give a short survey concerning the spectrum and the fine spectrum of the linear operators defined by some particular triangle matrices over certain sequence spaces. The fine spectrum of the Cesàro operator of order one on the sequence space ℓ_p studied by González [19], where 1 < p < ∞. Also, weighted mean matrices of operators on ℓ_p have been investigated by Cartlidge [20]. The spectrum of the Cesàro operator of order one on the sequence spaces bv₀ and bv investigated by Okutoyi [8, 21]. The spectrum and fine spectrum of the Rhally operators on the sequence spaces c₀, c, ℓ_p, bv, and bv₀ were examined by Yıldırım [9, 22–28]. The fine spectrum of the difference operator Δ over the sequence spaces c₀ and c was studied by Altay and Başar [12]. The same authors also worked the fine spectrum of the generalized difference operator B(r, s) over c₀ and c, in [29]. The fine spectra of Δ over ℓ₁ and bv studied by Kayaduman and Furkan [30]. Recently, the fine spectra of the difference operator Δ over the sequence spaces ℓ_p and bv_p studied by Akhmedov and Başar [31, 32], where bv_p is the space of p-bounded variation sequences and introduced by Başar and Altay [33] with 1 ⩽ p < ∞. Also, the fine spectrum of the generalized difference operator B(r, s) over the sequence spaces ℓ₁ and bv determined by Furkan et al. [34]. Recently, the fine spectrum of B(r, s, t) over the sequence spaces c₀ and c has been studied by Furkan et al. [35]. Quite recently, de Malafosse [11] and Altay and Başar [12] have, respectively, studied the spectrum and the fine spectrum of the difference operator on the sequence spaces s_r and c₀, c, where s_r denotes the Banach space of all sequences x = (x_k) normed by , (r > 0). Altay and Karakuş [36] have determined the fine spectrum of the Zweier matrix, which is a band matrix as an operator over the sequence spaces ℓ₁ and bv. Farés and de Malafosse [37] studied the spectra of the difference operator on the sequence spaces ℓ_p(α), where (α_n) denotes the sequence of positive reals and ℓ_p(α) is the Banach space of all sequences x = (x_n) normed by with p⩾1. Also the fine spectrum of the same operator over ℓ₁ and bv has been studied by Bilgiç and Furkan [13]. More recently the fine spectrum of the operator B(r, s) over ℓ_p and bv_p has been studied by Bilgiç and Furkan [38]. In 2010, Srivastava and Kumar [16] have determined the spectra and the fine spectra of generalized difference operator Δ_ν on ℓ₁, where Δ_ν is defined by (Δ_ν) _nn = ν_n and (Δ_ν) _n+1,n = −ν_n for all n ∈ ℕ, under certain conditions on the sequence ν = (ν_n), and they have just generalized these results by the generalized difference operator Δ_uv defined by Δ_uvx = (u_nx_n + v_n−1x_n−1) _n∈ℕ for all n ∈ ℕ, (see [18]). Altun [39] has studied the fine spectra of the Toeplitz operators, which are represented by upper and lower triangular n-band infinite matrices, over the sequence spaces c₀ and c. Later, Karakaya and Altun have determined the fine spectra of upper triangular double-band matrices over the sequence spaces c₀ and c, in [40]. Quite recently, Akhmedov and El-Shabrawy [15] have obtained the fine spectrum of the generalized difference operator Δ_a,b, defined as a double band matrix with the convergent sequences and having certain properties, over the sequence space c. Finally, the fine spectrum with respect to the Goldberg′s classification of the operator B(r, s, t) defined by a triple band matrix over the sequence spaces ℓ_p and bv_p with 1 < p < ∞ has recently been studied by Furkan et al. [14]. At this stage, Table 2 may be useful.

Table 2. Spectrum and fine spectrum of some triangle matrices in certain sequence spaces. In this paper, we study the fine spectrum of the generalized difference operator

defined by an upper double sequential band matrix acting on the sequence spaces ℓ_p with respect to the Goldberg′s classification. Additionally, we give the approximate point spectrum, defect spectrum, and compression spectrum of the matrix operator

over the spaces ℓ_p. We quote some lemmas, which are needed in proving the theorems given in Section 3.

σ(A, λ)	σ_p(A, λ)	σ_c(A, λ)	σ_r(A, λ)	refer to
	—	—	—	[4]
σ(W, c)	—	—	—	[5]
σ(C₁, c₀)	—	—	—	[6]
σ(C₁, c₀)	σ_p(C₁, c₀)	σ_c(C₁, c₀)	σ_r(C₁, c₀)	[7]
σ(C₁, bv)	—	—	—	[8]
σ(R, c₀)	σ_p(R, c₀)	σ_c(R, c₀)	σ_r(R, c₀)	[9]
σ(R, c)	σ_p(R, c)	σ_c(R, c)	σ_r(R, c)	[9]
	—	—	—	[10]
σ(Δ, s_r)	—	—	—	[11]
σ(Δ, c₀)	—	—	—	[11]
σ(Δ, c)	—	—	—	[11]
σ(Δ⁽¹⁾, c)	σ_p(Δ⁽¹⁾, c)	σ_c(Δ⁽¹⁾, c)	σ_r(Δ⁽¹⁾, c)	[12]
σ(Δ⁽¹⁾, c₀)	σ_p(Δ⁽¹⁾, c₀)	σ_c(Δ⁽¹⁾, c₀)	σ_r(Δ⁽¹⁾, c₀)	[12]
σ(B(r, s), ℓ_p)	σ_p(B(r, s), ℓ_p)	σ_c(B(r, s), ℓ_p)	σ_r(B(r, s), ℓ_p)	[13]
σ(B(r, s), bv_p)	σ_p(B(r, s), bv_p)	σ_c(B(r, s), bv_p)	σ_r(B(r, s), bv_p)	[13]
σ(B(r, s, t), ℓ_p)	σ_p(B(r, s, t), ℓ_p)	σ_c(B(r, s, t), ℓ_p)	σ_r(B(r, s, t), ℓ_p)	[14]
σ(B(r, s, t), bv_p)	σ_p(B(r, s, t), bv_p)	σ_c(B(r, s, t), bv_p)	σ_r(B(r, s, t), bv_p)	[14]
σ(Δ_a,b, c)	σ_p(Δ_a,b, c)	σ_c(Δ_a,b, c)	σ_r(Δ_a,b, c)	[15]
σ(Δ_ν, ℓ₁)	σ_p(Δ_ν, ℓ₁)	σ_c(Δ_ν, ℓ₁)	σ_r(Δ_ν, ℓ₁)	[16]
				[17]
σ(Δ_uv, ℓ₁)	σ_p(Δ_uv, ℓ₁)	σ_c(Δ_uv, ℓ₁)	σ_r(Δ_uv, ℓ₁)	[18]

Lemma 2.2 (see [41], p. 253, Theorem 34.16.)The matrix A = (a_nk) gives rise to a bounded linear operator T ∈ B(ℓ₁) from ℓ₁ to itself if and only if the supremum of ℓ₁ norms of the columns of A is bounded.

Lemma 2.3 (see [41], p. 245, Theorem 34.3.)The matrix A = (a_nk) gives rise to a bounded linear operator T ∈ B(ℓ_∞) from ℓ_∞ to itself if and only if the supremum of ℓ₁ norms of the rows of A is bounded.

Lemma 2.4 (see [41], p. 254, Theorem 34.18.)Let 1 < p < ∞ and A ∈ (ℓ_∞ : ℓ_∞)∩(ℓ₁ : ℓ₁). Then, A ∈ (ℓ_p : ℓ_p).

Let

and

be sequences whose entries either constants or distinct real numbers satisfying the following conditions:

(2.10)

Then, we define the sequential generalized difference matrix

(2.11)

Therefore, we introduce the operator

from ℓ_p to itself by

(2.12)

3. Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p

Theorem 3.1. The operator is a bounded linear operator and

(3.1)

Proof. Since the linearity of the operator is not difficult to prove, we omit the detail. Now we prove that (3.1) holds for the operator on the space ℓ_p. It is trivial that for e^(k) ∈ ℓ_p. Therefore, we have

(3.2)

which implies that

(3.3)

Let x = (x_k) ∈ ℓ_p, where p > 1. Then, since (s_kx_k+1), (r_kx_k) ∈ ℓ_p it is easy to see by Minkowski′s inequality that

(3.4)

which leads us to the result that

(3.5)

Therefore, by combining the inequalities in (3.3) and (3.5) we have (3.1), as desired.

Lemma 3.2 (see [42], p. 115, Lemma 3.1.)Let 1 < p < ∞. If

(3.6)

then the series

(3.7)

is not convergent.

Throughout the paper, by 𝒞 and 𝒮𝒟, we denote the set of constant sequences and the set of sequences of distinct real numbers, respectively.

Theorem 3.3.

(3.8)

Proof. Let for θ ≠ x ∈ ℓ_p Then, by solving linear equation

(3.9)

x_k = ((α − r_k)/s_k−1)x_k−1 for all k⩾1 and

(3.10)

Part 1. Assume that

. Let r_k = r and s_k = s For all k ∈ ℕ. We observe that x_k = ((α − r)/s) ^kx₀. This shows that x ∈ ℓ_p if and if only |α − r | <|s|, as asserted.

Part 2. Assume that . We must take x₀ ≠ 0, since x ≠ 0. It is clear that, for all k ∈ ℕ, the vector x = (x₀, x₁, …, x_k, 0,0, …) is an eigenvector of the operator corresponding to the eigenvalue α = r_k, where x₀ ≠ 0 and x_n = ((α − r_n)/s_n−1)x_n−1, for 1 ⩽ n ⩽ k. Thus . If r_k ≠ α, for all k ∈ ℕ, then x_k ≠ 0. If we take |α − r | <|s|, since lim _k→∞ | x_k+1/x_k|^p = lim _k→∞ | (r_k − α)/s_k|^p = |(r − α)/s|^p < 1, x ∈ ℓ_p. Hence . Conversely, let . Then, there exists x = (x₀, x₁, x₂, …) in ℓ_p and we have x_k = ((α − r_k)/s_k−1)x_k−1, for all k⩾1. Since x ∈ ℓ_p, we can use ratio test. And so lim _k→∞ | x_k+1/x_k|^p = lim _k→∞ | (r_k − α)/s_k|^p = |(r − α)/s|^p < 1 or α ∈ {r_k : k ∈ ℂ}. If |α − r | = |s|, by Lemma 3.2 x ∉ ℓ_p. This completes the proof.

Theorem 3.4.

(3.11)

Proof. We prove the theorem by dividing into two parts.

Part 1. Assume that . Consider for f ≠ θ = (0,0, 0, …) in . Then, by solving the system of linear equations

(3.12)

we find that f₀ = 0 if α ≠ r = r_k and f₁ = f₂ = ⋯ = 0 if f₀ = 0, which contradicts f ≠ θ. If

is the first nonzero entry of the sequence f = (f_n) and α = r, then we get

that implies

, which contradicts the assumption

. Hence, the equation

has no solution f ≠ θ.

Part 2. Assume that . Then, by solving the equation for f ≠ θ = (0,0, 0, …) in ℓ_q, we obtain (r₀ − α)f₀ = 0 and (r_k+1 − α)f_k+1 + s_kf_k = 0 for all k ∈ ℕ. Hence, for all α ∉ {r_k : k ∈ ℕ}, we have f_k = 0 for all k ∈ ℕ, which contradicts our assumption. So, . This shows that . Now, we prove that

(3.13)

, then, by solving the equation

for f ≠ θ = (0,0, 0, …) in ℓ_q with α = r₀,

(3.14)

which can expressed by the recursion relation

(3.15)

Using ratio test,

(3.16)

But |s/(r − r₀)| ≠ 1. Hence,

(3.17)

If we choose α = r_k ≠ r for all k ∈ ℕ₁, then we get f₀ = f₁ = f₂ = ⋯ = f_k−1 = 0 and

(3.18)

which can expressed by the recursion relation

(3.19)

Using ratio test,

(3.20)

But |s/(r − r_k)| ≠ 1. So we have

(3.21)

Conversely, let α ∈ ℬ. Then exist k ∈ ℕ, α = r_k ≠ r, and

(3.22)

That is, f ∈ ℓ_q. So we have

. This completes the proof.

Lemma 3.5 (see [3], p. 60.)The adjoint operator T^* of T is onto if and only if T is a bounded operator.

Theorem 3.6.

Proof. The proof is obvious so is omitted.

Theorem 3.7. Let (r_k), (s_k) in 𝒮𝒟 and 𝒞. .

Proof. By Theorems 3.4 and 3.6, .

Theorem 3.8. Let 𝒜 = {α ∈ ℂ : |r − α| ⩽ |s|} and ℬ = {r_k : k ∈ ℕ, |r − r_k | >|s|}. Then, the set ℬ is finite and .

Proof. We will show that is onto, for |r − α | >|s|. Thus, for every y ∈ ℓ_q, we find x ∈ ℓ_q. is triangle so it has an inverse. Also equation gives . It is sufficient to show that . We can calculate that as follows:

(3.23)

Therefore, the supremum of the ℓ₁ norms of the rows of

is S_k, where

(3.24)

(3.25)

Therefore,

(3.26)

where

(3.27)

Then, Mk₀⩾1 and so

(3.28)

But there exist k₁ ∈ ℕ and a real number p₁ such that 1/|r_k − α| < p₁ for all k⩾k₁. Then, S_k ⩽ (Mp₁k₀)/(1 − p₀) for all k > max {k₀, k₁}. Hence, sup _k∈ℕS_k < ∞. This shows that

. Similarly, we can show that

. By Lemma 2.4, we have

(3.29)

Hence,

is onto. By Lemma 3.5,

is bounded inverse. This means that

(3.30)

Combining this with Theorem 3.3 and Theorem 3.7, we get

(3.31)

and again from Theorem 3.3

and

. Since the spectrum of any bounded operator is closed, we have

(3.32)

Combining (3.31) and (3.32), we get

(3.33)

Theorem 3.9. Let (r_k), (s_k) in 𝒮𝒟 or 𝒞. .

Proof. The proof follows of immediately from Theorems 3.3, 3.7, and 3.8 because the parts , , and are pairwise disjoint sets and union of these sets is .

Theorem 3.10. Let (r_k), (s_k) ∈ 𝒮𝒟 and 𝒞. If |α − r | <|s|, .

Proof. From Theorem 3.3, . Thus, does not exist. It is sufficient to show that the operator is onto, that is, for given y = (y_k) ∈ ℓ_p, we have to find x = (x_k) ∈ ℓ_p such that . Solving the linear equation ,

(3.34)

let

(3.35)

Then, ∑_k | x_k|^p ⩽ sup _k(R_k) ^p∑_k | y_k|^p, where

(3.36)

for all k, n ∈ ℕ. Then, since

(3.37)

we have

(3.38)

Since |r − α | <|s|, (R_k) is a convergent sequence of positive real numbers with limit R. Hence, (R_k) bounded and we have sup _k(R_k) ^p < ∞. Therefore,

(3.39)

This shows that x = (x_k) ∈ ℓ_p. Thus

is onto. So we have

Theorem 3.11. Let (r_k), (s_k) ∈ 𝒞 with r_k = r, s_k = s for all k ∈ ℕ. Then, the following statements hold:

(i)
,
(ii)
,
(iii)
.

Proof. (i) Since from Table 1,

(3.40)

we have by Theorem 3.7

(3.41)

Hence,

(3.42)

(ii) Since the following equality:

(3.43)

holds from Table 1, we derive by Theorems 3.8 and 3.10 that

(iii) From Table 1, we have

(3.44)

By Theorem 3.4, it is immediate that .

Theorem 3.12. Let (r_k) ∈ 𝒮𝒟. Then

(3.45)

Proof. We have by Theorem 3.4 and Part (e) of Proposition 2.1 that

(3.46)

By Theorems 3.7 and 3.4, we must have

(3.47)

Hence,

. Additionally, since

Therefore, we derive from Table 1, Theorems 3.8, and 3.10 that

(3.48)

4. Conclusion

In the present work, as a natural continuation of Akhmedov and El-Shabrawy [15] and Srivastava and Kumar [18], we have determined the spectrum and the fine spectrum of the double sequential band matrix on the space ℓ_p. Many researchers determine the spectrum and fine spectrum of a matrix operator in some sequence spaces. In addition to this, we add the definition of some new divisions of spectrum called as approximate point spectrum, defect spectrum, and compression spectrum of the matrix operator and give the related results for the matrix operator on the space ℓ_p, which is a new development for this type works giving the fine spectrum of a matrix operator on a sequence space with respect to the Goldberg′s classification.

Acknowledgment

The authors would like to express their gratitude to Professor Feyzi Basar, Fatih University, Faculty of Art and Sciences, Department of Mathematics, The Hadımköy Campus, Büyükçekmece, Turkey, for his careful reading and for making some useful corrections, which improved the presentation of the paper.

References

1 Kreyszig E., Introductory Functional Analysis with Applications, 1978, John Wiley & Sons, New York, NY, USA, 0467220.
Google Scholar
2 Appell J., Pascale E., and Vignoli A., Nonlinear Spectral Theory, 2004, 10, Walter de Gruyter, Berlin, Germany, de Gruyter Series in Nonlinear Analysis and Applications, https://doi.org/10.1515/9783110199260, 2059617.
10.1515/9783110199260
Google Scholar
3 Goldberg S., Unbounded Linear Operators, 1985, Dover Publications, New York, NY, USA, 810617.
Google Scholar
4 Wenger R. B., The fine spectra of the Hölder summability operators, Indian Journal of Pure and Applied Mathematics. (1975) 6, no. 6, 695–712, 0445150, ZBL0362.40010.
Google Scholar
5 Rhoades B. E., The fine spectra for weighted mean operators, Pacific Journal of Mathematics. (1983) 104, no. 1, 219–230, 683739, ZBL0501.40007.
10.2140/pjm.1983.104.219
Web of Science® Google Scholar
6 Reade J. B., On the spectrum of the Cesàro operator, The Bulletin of the London Mathematical Society. (1985) 17, no. 3, 263–267, https://doi.org/10.1112/blms/17.3.263, 806429, ZBL0548.47017.
10.1112/blms/17.3.263
Web of Science® Google Scholar
7 Akhmedov A. M. and Başar F., On the fine spectrum of the Cesàro operator in c₀, Mathematical Journal of Ibaraki University. (2004) 36, 25–32, https://doi.org/10.5036/mjiu.36.25, 2105631, ZBL1096.47031.
10.5036/mjiu.36.25
Google Scholar
8 Okutoyi J. I., On the spectrum of C₁ as an operator on bv, Communications de la Faculté des Sciences de l′Université d′Ankara A1. (1992) 41, no. 1-2, 197–207, 1329011, ZBL0831.47020.
Google Scholar
9 Yıldırım M., On the spectrum and fine spectrum of the compact Rhaly operators, Indian Journal of Pure and Applied Mathematics. (1996) 27, no. 8, 779–784, 1400114, ZBL0859.47004.
Web of Science® Google Scholar
10 Coşkun C., The spectra and fine spectra for p-Cesàro operators, Turkish Journal of Mathematics. (1997) 21, no. 2, 207–212, 1469965.
Google Scholar
11 de Malafosse B., Properties of some sets of sequences and application to the spaces of bounded difference sequences of order μ, Hokkaido Mathematical Journal. (2002) 31, no. 2, 283–299, 1914961, ZBL1016.40002.
10.14492/hokmj/1350911865
Google Scholar
12 Altay B. and Başar F., On the fine spectrum of the difference operator Δ on c₀ and c, Information Sciences. (2004) 168, no. 1–4, 217–224, https://doi.org/10.1016/j.ins.2004.02.007, 2117290, ZBL1085.47041.
10.1016/j.ins.2004.02.007
Web of Science® Google Scholar
13 Bilgiç H. and Furkan H., On the fine spectrum of the operator B(r, s, t) over the sequence spaces l₁ and bv, Mathematical and Computer Modelling. (2007) 45, no. 7-8, 883–891, https://doi.org/10.1016/j.mcm.2006.08.008, 2297129, ZBL1152.47024.
10.1016/j.mcm.2006.08.008
Google Scholar
14 Furkan H., Bilgiç H., and Başar F., On the fine spectrum of the operator B(r, s, t) over the sequence spaces ℓ_p and bv_p, (1 < p < ∞), Computers & Mathematics with Applications. (2010) 60, no. 7, 2141–2152, https://doi.org/10.1016/j.camwa.2010.07.059, 2719736, ZBL1222.47050.
10.1016/j.camwa.2010.07.059
Web of Science® Google Scholar
15 Akhmedov A. M. and El-Shabrawy S. R., On the fine spectrum of the operator Δ_a,b over the sequence space c, Computers & Mathematics with Applications. (2011) 61, no. 10, 2994–3002, https://doi.org/10.1016/j.camwa.2011.03.085, 2799825, ZBL1222.40002.
10.1016/j.camwa.2011.03.085
Web of Science® Google Scholar
16 Srivastava P. D. and Kumar S., Fine spectrum of the generalized difference operator Δ_v on sequence space l₁, Thai Journal of Mathematics. (2010) 8, no. 2, 7–19, 2763685, ZBL1236.47029.
Google Scholar
17 Panigrahi B. L. and Srivastava P. D., Spectrum and fine spectrum of generalized second order difference operator on sequence space c₀, Thai Journal of Mathematics. (2011) 9, no. 1, 57–74, 2833753.
Google Scholar
18 Srivastava P. D. and Kumar S., Fine spectrum of the generalized difference operator Δ_uv on sequence space l₁, Applied Mathematics and Computation. (2012) 218, no. 11, 6407–6414, https://doi.org/10.1016/j.amc.2011.12.010, 2879121.
10.1016/j.amc.2011.12.010
Web of Science® Google Scholar
19 González M., The fine spectrum of the Cesàro operator in ℓ_p(1 < p < ∞), Archiv der Mathematik. (1985) 44, no. 4, 355–358, https://doi.org/10.1007/BF01235779, 788950, ZBL0568.47021.
10.1007/BF01235779
Web of Science® Google Scholar
20 Cartlidge P. J., Weighted mean matrices as operators on lp [Ph.D. thesis], 1978, Indiana University.
Google Scholar
21 Okutoyi J. I., On the spectrum of C₁ as an operator on bv₀, Journal of the Australian Mathematical Society A. (1990) 48, no. 1, 79–86, 1026838, https://doi.org/10.1017/S1446788700035205, ZBL0691.40004.
10.1017/S1446788700035205
Web of Science® Google Scholar
22 Yıldırım M., On the spectrum of the Rhaly operators on c₀ and c, Indian Journal of Pure and Applied Mathematics. (1998) 29, no. 12, 1301–1309, 1671344, ZBL0928.47016.
Web of Science® Google Scholar
23 Yıldırım M., On the spectrum of the Rhaly operators on l_p, Indian Journal of Pure and Applied Mathematics. (2001) 32, no. 2, 191–198, 1820858, ZBL0989.47023.
Web of Science® Google Scholar
24 Yıldırım M., The fine spectra of the Rhaly operators on c₀, Turkish Journal of Mathematics. (2002) 26, no. 3, 273–282, 1922705, ZBL1038.47025.
Google Scholar
25 Yıldırım M., On the spectrum of the Rhaly operators on bv, East Asian Mathematical Journal. (2002) 18, 21–41.
Google Scholar
26 Yıldırım M., On the spectrum and fine spectrum of the compact Rhaly operators, Indian Journal of Pure and Applied Mathematics. (2003) 34, no. 10, 1443–1452, 2024786, ZBL1073.47039.
Web of Science® Google Scholar
27 Yildirim M., On the spectrum of the Rhaly operators on bv₀, Communications of the Korean Mathematical Society. (2003) 18, no. 4, 669–676, https://doi.org/10.4134/CKMS.2003.18.4.669, 2048264, ZBL1101.47308.
10.4134/CKMS.2003.18.4.669
Google Scholar
28 Yildirim M., On the fine spectrum of the Rhaly operators on lp, East Asian Mathematical Journal. (2004) 20, 153–160.
Google Scholar
29 Altay B. and Başar F., On the fine spectrum of the generalized difference operator B(r, s) over the sequence spaces c₀ and c, International Journal of Mathematics and Mathematical Sciences. (2005) 2005, no. 18, 3005–3013, https://doi.org/10.1155/IJMMS.2005.3005, 2199607, ZBL1098.39013.
10.1155/IJMMS.2005.3005
Google Scholar
30 Kayaduman K. and Furkan H., The fine spectra of the difference operator Δ over the sequence spaces l₁ and bv, International Mathematical Forum. (2006) 1, no. 24, 1153–1160, 2256672, ZBL1119.47306.
10.12988/imf.2006.06093
Google Scholar
31 Akhmedov A. M. and Başar F., On the fine spectra of the difference operator Δ over the sequence space ℓ_p, Demonstratio Mathematica. (2006) 39, no. 3, 585–595, 2262007, ZBL1118.47303.
10.1515/dema-2006-0313
Google Scholar
32 Akhmedov A. M. and Başar F., On the fine spectra of the difference operator Δ over the sequence space bv_p, (1 ≤ p < ∞), Acta Mathematica Sinica. (2007) 23, no. 10, 1757–1768, https://doi.org/10.1007/s10114-005-0777-0, 2352291, ZBL1134.47025.
10.1007/s10114-005-0777-0
Web of Science® Google Scholar
33 Başar F. and Altay B., On the space of sequences of p-bounded variation and related matrix mappings, Ukrainian Mathematical Journal. (2003) 55, no. 1, 136–147, https://doi.org/10.1023/A:1025080820961, 2034909.
10.1023/A:1025080820961
Google Scholar
34 Furkan H., Bilgiç H., and Kayaduman K., On the fine spectrum of the generalized difference operator B(r, s) over the sequence spaces l₁ and bv, Hokkaido Mathematical Journal. (2006) 35, no. 4, 897–908, 2289365.
10.14492/hokmj/1285766434
Google Scholar
35 Furkan H., Bilgiç H., and Altay B., On the fine spectrum of the operator B(r, s, t) over c₀ and c, Computers & Mathematics with Applications. (2007) 53, no. 6, 989–998, https://doi.org/10.1016/j.camwa.2006.07.006, 2333342, ZBL1152.47024.
10.1016/j.camwa.2006.07.006
Web of Science® Google Scholar
36 Altay B. and Karakuş M., On the spectrum and the fine spectrum of the Zweier matrix as an operator on some sequence spaces, Thai Journal of Mathematics. (2005) 3, no. 2, 153–162, 2306327, ZBL1183.47027.
Google Scholar
37 Farés A. and de Malafosse B., Spectra of the operator of the first difference in and l_p(α)(1 ≤ p < ∞) and application to matrix transformations, Demonstratio Mathematica. (2008) 41, no. 3, 661–676, 2433316, ZBL1157.47027.
10.1515/dema-2008-0318
Google Scholar
38 Bilgiç H. and Furkan H., On the fine spectrum of the generalized difference operator B(r, s) over the sequence spaces l_p and bv_p(1 < p < ∞), Nonlinear Analysis. (2008) 68, no. 3, 499–506, https://doi.org/10.1016/j.na.2006.11.015, 2372360, ZBL1139.47005.
10.1016/j.na.2006.11.015
Web of Science® Google Scholar
39 Altun M., On the fine spectra of triangular Toeplitz operators, Applied Mathematics and Computation. (2011) 217, no. 20, 8044–8051, https://doi.org/10.1016/j.amc.2011.03.003, 2802215.
10.1016/j.amc.2011.03.003
Web of Science® Google Scholar
40 Karakaya V. and Altun M., Fine spectra of upper triangular double-band matrices, Journal of Computational and Applied Mathematics. (2010) 234, no. 5, 1387–1394, https://doi.org/10.1016/j.cam.2010.02.014, 2610354, ZBL1193.47006.
10.1016/j.cam.2010.02.014
Web of Science® Google Scholar
41 Choudhary B. and Nanda S., Functional Analysis with Applications, 1989, John Wiley & Sons, New York, NY, USA, 1028774.
Google Scholar
42 El-Shabrawy S. R., On the fine spectrum of the generalized difference operator Δ_a,b over the sequence l_p, (1 < p < ∞), Applied Mathematics & Information Sciences. (2012) 6, no. 1, supplement, 111S–118S.
Google Scholar

Citing Literature

All articles

Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p, (1 < p < ∞)

Abstract

1. Introduction

2. Subdivisions of the Spectrum

2.1. The Point Spectrum, Continuous Spectrum, and Residual Spectrum

2.2. The Approximate Point Spectrum, Defect Spectrum, and Compression Spectrum

2.3. Goldberg′s Classification of Spectrum

3. Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p

4. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓp, (1 < p < ∞)

Abstract

1. Introduction

2. Subdivisions of the Spectrum

2.1. The Point Spectrum, Continuous Spectrum, and Residual Spectrum

2.2. The Approximate Point Spectrum, Defect Spectrum, and Compression Spectrum

2.3. Goldberg′s Classification of Spectrum

3. Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓp

4. Conclusion

Acknowledgment

References

Citing Literature

Figures

References

Related

Information

Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p, (1 < p < ∞)

3. Fine Spectra of Upper Triangular Double-Band Matrices over the Sequence Space ℓ_p