Journal of Applied Mathematics
Volume 2012, Issue 1 371729
Research Article
Open Access

Exact Matrix Representation of the Transverse Magnetic Multiple Scattering of Obliquely Incident Plane Waves by the Diffraction Grating of Penetrable Cylinders

Ömer Kavaklıoğlu, 

Corresponding Author

Ömer Kavaklıoğlu

Division of Electromagnetics Research, Department of Electrical and Computer Engineering, School of Engineering and Applied Science, The George Washington University, Washington, DC 20052, USA gwu.edu

Division of Electromagnetic Fields and Microwave Techniques, Department of Electrical and Electronics Engineering, Faculty of Engineering and Architecture, İzmir Kâtip Çelebi University, 35620 Çiğli, İzmir, Turkey gwu.edu

Search for more papers by this author
Roger Henry Lang, 

Roger Henry Lang

Division of Electromagnetics Research, Department of Electrical and Computer Engineering, School of Engineering and Applied Science, The George Washington University, Washington, DC 20052, USA gwu.edu

Search for more papers by this author
First published: 05 July 2012
https://doi.org/10.1155/2012/371729
Citations: 1
Academic Editor: Renat Zhdanov

Abstract

“An exact matrix conformation model” associated with the equations describing the exact behavior of the Fourier-Bessel multiple scattering coefficients of the diffraction grating consisting of an infinite number of infinitely long parallel penetrable circular cylinders, corresponding to the obliquely incident transverse-magnetic plane waves in “Twersky-Wait-Kavaklıoğlu representation,” originally excogitated in (Kavaklıoğlu, 2000), is acquired, and the exact solution for “the Fourier-Bessel multiple scattering coefficients of the diffraction grating at oblique incidence” is obtained by a matrix inversion procedure.

1. Introduction

Twersky [1] solved the problem of multiple scattering of radiation by an arbitrary configuration of parallel cylinders by the infinite grating of insulating dielectric circular cylinders at normal incidence in terms of cylindrical wave functions as long ago as 1952, considering all possible contributions to the excitation of a particular cylinder by the radiation scattered by the remaining cylinders. He later extended his solution for the case where all axes of cylinders lie in the same plane [2] by expressing the scattered wave as an infinite sum of orders of scattering and derived the solution for the scattering of waves by the finite grating of cylinders [3] at normal incidence. In addition, Twersky introduced a “scalar functional equation” [4] for the grating in order to describe the relationship between the multiple scattered amplitude of the grating in terms of the “multiple scattered amplitude of an isolated cylinder within the grating.” He [5] then utilized the separation-of-variables technique to derive a set of algebraic equations for the “multiple scattering coefficients of the infinite grating” in terms of his famous elementary function representations of “Schlömilch series” [6], and in terms of the “well-known scattering coefficients of an isolated cylinder at normal incidence,” which was originally derived by Rayleigh [7, 8]. His results since then have been reiterated and extensively used by many other authors.

For the more generalized case of conical incidence, Sivov [9] first studied the problem of determining the coefficients of reflection and transmission by an infinite plane grating of parallel conductors assuming the period small in comparison with the wavelength. Lee [10] treated the multiple scattering by an arbitrary configuration of parallel, nonoverlapping infinite cylinders, and provided the solution for the “scattering by closely spaced radially-stratified parallel cylinders with an arbitrary number of stratified layers” [11]. Furthermore, Smith et al. [12] developed a formulation for cylinder gratings in conical incidence using a multipole method in modeling photonic crystal structures and study scattering matrices and “Bloch modes” in order to investigate the photonic band gap properties of woodpile structures [13]. In a more recent study, Henin et al. [14] presented a semianalytical solution by an array of circular dielectric cylinders and parallel-coated circular cylinders of arbitrary radii and positions [15].

The exact equations describing the behavior of the Fourier-Bessel multiple scattering coefficients of an infinite grating of dielectric circular cylinders, which are aligned along the y-axis and parallel to the z-axis, for obliquely incident plane electromagnetic waves, θi being the obliquity angle made with z-axis, were first derived by Kavaklıoğlu [16–18] for both TM and TE polarizations. The generalized representations associated with the reflected and transmitted fields were formulated in terms of these Fourier-Bessel multiple scattering coefficients for obliquely incident plane H-polarized waves in Kavaklıoğlu and Schneider [19]. In addition, they [20] derived the generalized form of Twersky’s functional equation [4] for the infinite grating at oblique incidence in matrix form in terms of the “Fourier-Bessel scattering coefficients of an isolated dielectric circular cylinder at oblique incidence” originally derived by Wait [21]. Moreover, Kavaklıoğlu and Schneider [22] acquired the asymptotic solution for the Fourier-Bessel multiple scattering coefficients of the infinite grating associated with obliquely incident and vertically polarized waves up to and including third order as a function of the cylinder radius to grating spacing when the grating spacing “d” is small compare to a wavelength. Recently, Kavaklıoğlu and Lang [23] demonstrated a rigorous proof for the validity of this asymptotic solution derived in [22].

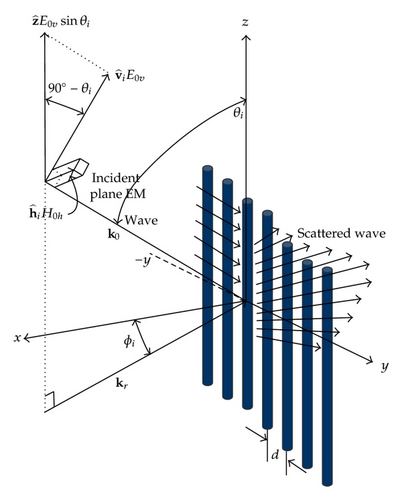
The purpose of this investigation is to acquire the exact conformation model for the Fourier-Bessel multiple scattering coefficients of an infinite array of penetrable circular cylinders associated with obliquely incident vertically polarized plane electromagnetic waves and to capture the exact representation of the aforementioned coefficients of the diffraction grating at oblique incidence in “matrix form.” In the generalized oblique incidence solution presented in this article, the direction of the incident plane wave makes an arbitrary oblique angle of arrival θi with the positive z-axis as depicted in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The configuration of the problem of scattering of waves by an infinite array of penetrable circular cylinders at oblique incidence (side view).

In addition, we have explicated and connoted that our proposed method of solution for the scattering coefficients is a new technique and an exact representation. Besides, the paper clearly describes how one can generate a numerical algorithm from this exact solution by the truncation of the system matrices associated with the undetermined multiple scattering coefficients. On the other hand, the objective of this paper is not to discover some numerical algorithm as its title designates, which would be completely approximate and requiring an error analysis.

2. Description of the Transverse Magnetic Multiple Scattering Coefficients of the Infinite Array at Oblique Incidence

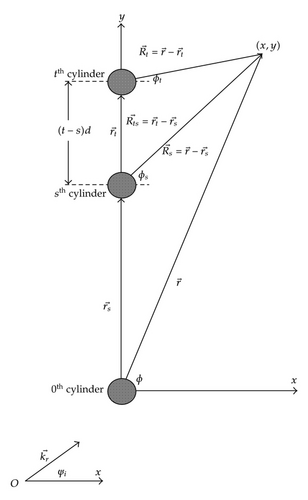
We consider a vertically polarized obliquely incident plane electromagnetic wave upon an infinite array of insulating circular dielectric cylinders having infinite length with radii a, dielectric constant εr, and relative permeability μr. The constituent cylinders of the infinite array are placed periodically along the y-axis, with their axis parallel to the z-axis, located at positions r0, r1, r2,…, and so forth, and separated by a distance of d.

For this configuration, the incident wave can be written in the cylindrical coordinate system (Rs, ϕs, z) of the sth cylinder in terms of the cylindrical waves referred to the axis of sth cylinder [16] as
()
In the representation above, denotes the vertical polarization vector associated with a unit vector having a component parallel to all the cylinders, ϕi is the angle of incidence in x-y plane measured from x-axis in such a way that ψi = π + ϕi as it is delineated in Figure 1, implying that the wave is arbitrarily incident in the first quadrant of the coordinate system, and Jn(x) denotes Bessel function of order n. In expression (2.1), we have
()
where k0 denotes the free space wave number with k0 : = 2π/λ0 and where λ0 is the wavelength of the incident radiation; θi is the obliquity angle made with z-axis. e−iωt time dependence is suppressed throughout the article, where ω represents the angular frequency of the incident wave in radians per second and t stands for time in seconds (Figure 2).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The geometry of the infinite grating problem (top view).
The exact solution associated with the z-component of the electric field intensity in the exterior of the infinite grating can be expressed in terms of the incident electric field in the coordinate system of the sth cylinder located at rs, plus a summation of cylindrical waves outgoing from the individual nth cylinder located at rn, which satisfies Silver-Müller radiation condition as |r − rn| → ∞, that is,
()
The generalized exact representation of the multiple scattered fields by an infinite grating of dielectric cylinders for obliquely incident plane waves has been rigorously treated by Kavaklıoğlu [16] for an arbitrary oblique angle of arrival θi with the positive z-axis, and it has been proved that the z-component of the total electric and magnetic fields in the exterior of the infinite grating for obliquely incident and vertically polarized plane electromagnetic waves can be written as
()
The infinite set of undetermined coefficients arising in (2.4) denotes the Fourier-Bessel multiple scattering coefficients for the infinite array of insulating dielectric cylinders corresponding to the vertically polarized obliquely incident plane electromagnetic waves, for  all  n ∈ Z where Z represents the set of all integers, and in (2.4) is given as
()
In addition, Qn and represent the multiple scattering effects, which are expressed as a linear combination of the undetermined Fourier-Bessel multiple scattering coefficients of the infinite grating at oblique incidence as
()
for all n ∈ Z. 𝒥n(krd) is the generalized form of the Schlömilch series for obliquely incident waves (Twersky [4–6], Kavaklıoğlu [18]) explicitly given as
()
where, Δ ≡ krd/2π  and denotes the nth order Hankel function of first kind, for all n ∈ Z. The series 𝒥n−m(krd) in expression (2.7) is the generalization of the “Schlömilch series for obliquely incident electromagnetic waves” (Twersky [6], Kavaklıoğlu [18]) and converges provided that krd(1 ± sin     ψi)/2π does not equal integers. The integral values of krd(1 ± sin  ψi)/2π are known as the “grazing modes” or “Rayleigh values” (Twersky [6]).

3. The Generalized Fourier-Bessel Multiple Scattering Coefficients of the Infinite Grating for Vertically Polarized Obliquely Incident Plane Electromagnetic Waves in Matrix Form

The equations describing the scattering coefficients for vertically polarized and obliquely incident plane electromagnetic waves are first derived in Kavaklıoğlu [16], which can be described as
()
for  all  n ∈ Z. In the equations above, we have
()
()
()
for all n ∈ Z for  ζ ∈ {ε, μ}, where k1 is defined as , F is defined as
()
and c stands for the speed of light in free space as
()
and in expression (3.3) and (3.4) are described as the first derivatives of these functions with respect to their arguments, that is, and .
Introducing the intrinsic impedance of free space as
()
two parameters that appears in the equations of the Fourier-Bessel multiple scattering coefficients of the infinite grating in (3.1), namely, and , can be acquired by employing (3.7) in (3.4) for ζ ∈ {ε, μ} as
()
for all n ∈ Z. Rearranging the equations in (3.1), we have modified the equations for the Fourier-Bessel multiple scattering coefficients as
()
for all n ∈ Z. Equations (3.9) for the special case of n = 0 can be simplified as
()
Or equivalently, (3.10) can be written as
()
for the Fourier-Bessel multiple scattering associated with the scattered electric and magnetic fields, respectively. Indicating those scattering coefficients corresponding to A0 and explicitly in (3.9), we have
()
{∀n ∈ Z∣n ≠ 0}. We have noticed that the equations (3.11) represent the solutions for A0 and which are expressed in terms of all the other Fourier-Bessel multiple scattering coefficients , {∀n ∈ Z∣n ≠ 0}. Therefore, we can insert these solutions of A0 and into (3.11) to eliminate A0 and terms from the equations of the scattering coefficients. For this purpose, we have first used (3.11) in the evaluation of the following identities as
()
{∀n ∈ Z∣n ≠ 0}. Using (3.13) in (3.12), we have acquired the equations for the scattering coefficients of the infinite grating of circular dielectric cylinders as
()
{∀  n ∈ Z∣n ≠ 0}. The equations in (3.14) together represent the complete set of equations for the Fourier-Bessel multiple scattering coefficients of the infinite grating of circular dielectric cylinders at oblique incidence. Incorporating the first terms inside the brackets into the infinite summation, (3.14) can be written more compactly as
()
{∀n ∈ Z∣n ≠ 0}. The equations in (3.15) represent the complete set of equations for the Fourier-Bessel multiple scattering coefficients and ’s of the infinite grating at oblique incidence. On the other hand, and are obtained from (3.10) in terms of all the other scattering coefficients, i.e., and ’s, {∀n ∈ Z∣n ≠ 0}. Defining a new set of parameters , ∀ζ ∈ {ε, μ}; and , {∀n ∈ Z∣n ≠ 0}, and {∀m ∈ Z∣m ≠ 0} as
()
()
()
and employing the expressions (3.16), (3.17), and (3.18) in the equations (3.15), we can express the equations for the generalized Fourier-Bessel multiple scattering coefficients of the infinite grating associated with obliquely incident and vertically polarized waves more compactly as
()
{∀n ∈ Z∣n ≠ 0}. We have obtained the following matrix equations from (3.19) as
()
In (3.20), we have defined
()
{∀n ∈ Z∣n ≠ 0}, where is an (∞ × ∞) diagonal matrix, defined for ζ ∈ {ε, μ}, and its elements , are given in (3.3),
()
where is an(∞ × ∞)  diagonal matrix defined for ζ ∈ {ε, μ} and its elements, , are given in (3.4),
()
where is an (∞ × ∞) diagonal matrix, and its elements, cn, are given in (3.2),
()
where is an (∞ × ∞) matrix, defined for  ζ ∈ {ε, μ}, and its elements, , are given in (3.16), and is an (∞ × ∞) identity matrix. Besides, we have
()
where and are (∞ × 1) vectors, and their elements , and are given in (3.17) and (3.18), respectively. On the other hand, the unknown scattering coefficients associated with the exterior electric and magnetic fields are defined as
()
and are (∞ × 1) unknown vectors for the Fourier-Bessel multiple scattering coefficients of the electric and magnetic fields of the infinite array of dielectric circular cylinders corresponding to the vertically polarized obliquely incident plane electromagnetic waves. We can use the definitions of (3.21)–(3.26) in combining (3.20) into a single matrix system of equations for the scattering coefficients of the infinite grating at oblique incidence, and write (3.20) as a unique matrix system of equation for all of the scattering coefficients as
()

4. Exact Solution to the “Twersky-Wait-Kavaklıoğlu Equations” for an Infinite Grating of Circular Dielectric Cylinders at Oblique Incidence: Transverse-Magnetic Mode

The purpose of this section is to acquire the solution to the exact matrix system of equations for transverse magnetic Fourier-Bessel multiple scattering coefficients of the infinite grating at oblique incidence. The matrix system of equations for the scattering coefficients of the exterior electric and magnetic fields corresponding to the vertically polarized obliquely incident plane electromagnetic waves expressed by (3.27) can be rewritten as two separate matrix equations as
()
()
From (4.1) we can solve for as
()
In a similar manner, we can solve from (4.2) for as
()
Using the expression of (4.4) for in (4.3), we have obtained the solution for as
()
or, equivalently
()
Defining two (∞ × ∞)  matrices in terms of the previously defined matrices, namely,
()
and inserting (4.7) into (4.5), (4.6), we can express as
()
Further evaluation of the expression (4.8) yields the multiple scattering coefficients for the electric fields in the exterior region of the infinite grating associated with obliquely incident vertically polarized electromagnetic waves, namely, as
()
Inserting the expression of in (4.9) into in (4.4), we have finally obtained the multiple scattering coefficients for the magnetic fields in the exterior region of the infinite grating associated with obliquely incident vertically polarized electromagnetic waves as
()
Combining (4.9) and (4.10) into a single matrix expression, we can write
()
This is the complete solution vector for the whole Fourier-Bessel multiple scattering coefficients of the infinite grating at oblique incidence.

5. Conclusion

In the closely related previous studies, the exact representations of the external fields corresponding to the obliquely incident plane electromagnetic waves and the exact equations describing the behavior of the associated Fourier-Bessel multiple scattering coefficients of an infinite array of penetrable circular cylinders, which are aligned along the y-axis and placed parallel to the z-axis, were derived [16–19] for both TM and TE polarizations. Furthermore, the generalized form of Twersky’s functional equation for the infinite grating at oblique incidence in matrix form was acquired [20] in terms of the Fourier-Bessel scattering coefficients of an isolated dielectric circular cylinder at oblique incidence, which was originally derived by Wait [21]. In a more recent treatment, by the implementation of the Ansatz proposed in [22], the asymptotic solution of the Fourier-Bessel multiple scattering coefficients associated with the obliquely incident and vertically polarized waves has been acquired as a function of cylinder radius to grating spacing up to and including the third order terms when the grating spacing, d, is small compare to a wavelength. In addition, a proof [23] for the validity of the asymptotic solution acquired in [22], have been provided.

In this investigation, we have presented a procedure for acquiring the conformation of the exact equations describing the behavior of the generalized Fourier-Bessel multiple scattering coefficients of an infinite array of penetrable circular cylinders associated with obliquely incident transverse magnetic plane waves in matrix form. This exact representation is formulated in terms of the multiplication of the two (∞ × ∞)  system matrices, and describes the exact solutions associated with the transverse magnetic multiple scattering coefficients at oblique incidence. Approximate expressions for the aforementioned multiple scattering coefficients can then easily be acquired by truncating these (∞ × ∞)  system matrices.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.