This paper considers a rumor transmission model with incubation that incorporates constant recruitment and has infectious force in the latent period and infected period. By carrying out a global analysis of the model and studying the stability of the rumor-free equilibrium and the rumor-endemic equilibrium, we use the geometric approach for ordinary differential equations which is based on the use of higher-order generalization of Bendixson’s criterion. It shows that either the number of rumor infective individuals tends to zero as time evolves or the rumor persists. We prove that the transcritical bifurcation occurs at R₀ crosses the bifurcation threshold R₀ = 1 by projecting the flow onto the extended center manifold. Since the rumor endemic level at the equilibrium is a continuous function of R₀, as a consequence for successful eradication of the rumor, one should simply reduce R₀ continuously below the threshold value 1. Finally, the obtained results are numerically validated and then discussed from both the mathematical and the sociological perspectives.

1. Introduction

Rumor is an important form of social interaction, and its spreading has a significant impact on human lives. Hayakawa [1] defines rumor as a kind of social phenomenon that a similar remark spreads on a large scale in a short time through chains of communication. Shibutani [2] regards rumor as collective problem solving, in which people “caught” in ambiguous situations try to caught “construe a meaningful interpretation…by pooling their intellectual resources.” Rumors may contain confidential information about public figures or news which concerns important social issues; they can shape the public opinion of a society or a market by affecting the individual beliefs of its members [3], and its spreading plays a significant role in a variety of human affairs.

Actually, the population dynamics underlying the diffusion of ideas holds many qualitative similarities to those involved in the spread of infections. In this paper, we apply a model similar to that used in epidemiology to the “transmission of a rumor.” To analyze the spreading and cessation of them, rumor transmissions are often modeled as social contagion processes. Pioneering contributions to their modeling are based on epidemiological models [4–6]. Therefore, the tracks of works on rumor spreading are closely relevant to epidemiological models [7–9], which involve the spread of a disease and the removal of infectious individuals. These models typically divide a population into classes that reflect the epidemiological status of individuals (e.g., susceptible, infected, recovered, etc.), who in turn transit between classes via mutual contact at given average rates. In this way, the models can capture average disease progression by tracking the mean number of people who are infected, who are prone to catch the disease, and who have recovered over time.

In this paper, we apply models similar to those used in epidemiology to the spread of rumor. By the term “rumor,” we refer generally to any concept that can be transmitted from person to person. It may refer to uncertain information, which takes time to discern between true and false, but it may also be a more fickle piece of information such as a colloquialism or a piece of news. What is important is that it is possible to tell if someone has adopted the rumor, understands and remembers it, and is capable of and/or active in spreading it to others.

The classical models for the spread of rumor were introduced by Daley and Kendall [10] and Maki and Thompson [11], and then many researchers have used the model extensively in the past for their quantitative studies [12–19]. In classical models, people are divided into three classes: ignorants (those not aware of the rumor), spreaders (those who are spreading it), and stiflers (those who know the rumor but have ceased communicating it after meeting somebody already informed), and they interact by pairwise contacts. In the Daley-Kendall (D-K) model, spreader-ignorant contact will convert the ignorant to spreader; spreader-spreader contact will convert both spreaders to stiflers; spreader-stifler contact will stifle the spreader. In the Maki-Thompson (M-T) model, the rumor is spread by directed contact of the spreaders with other individuals. Hence, when a spreader contacts another spreader, only the initiating one becomes a stifler. Bettencourt et al. [9] have worked on the spreading process of multiple varying ideas. Huang [14] studied the rumor spreading process with denial and skepticism, two models are established to accommodate skeptics. Kawachi [18] proposed and mathematically analyzed deterministic models for rumor transmission, which is extension of the deterministic D-K model. In Kawachi′s other extension model [19], he and his cooperators studied a flexible spreader-ignorant-stifler model where spreader-to-ignorant and stifler-to-spreader transitions are possible, while Lebensztayn and Machado [20] investigated the case where a new uninterested class of people exists. Pearce [21] and Gani [22] analyzed the probability generating functions in the stochastic rumor models by means of block-matrix methodology. In addition, Dickinson and Pearce [23] studied stochastic models for more general transient processes including epidemics and economics. In fact, independently of this series of studies, deterministic models for rumor transmission have been studied sporadically.

A number of studies proposed more complex models of rumor spreading based on several classical models of social networks including homogeneous networks, Erdos-Renyi (ER) random graphs, uncorrelated scale-free networks, and scale-free networks with assortative degree correlations [24–33], in particular those which were mediated by the internet, such as “virtual” communities and email networks. Those extended models include a general class of Markov processes for generating time-dependent evolution, and studies of the effects of social landscapes on the spread, either through Monte Carlo simulations over scale-free [34] or small-world [24] networks, but major shortcomings of these models were that either they neglected the topological characteristics of social networks or some of these models were not suitable for large-scale spreading process. Actually, Moreno et al. [34] studied the stochastic D-K model on scale-free networks and insisted that the uniformity of networks had a significant impact on the dynamic mechanism of rumor spreading. Isham et al. [26] studied the final size distribution of rumors on general networks. Sudbury [27] studied dynamic mechanisms of information transmission on social networks and insisted that the dynamic behavior of rumor spreading matched SIR model. As for applications, Zanette [24, 28] and Buzna et al. [31] established rumor spreading model on the small-world networks and found the existence of rumor spreading critical value. Liu et al. [32] revealed that the final percentage of population who heard the rumor decreases with a network structure parameter p; this idea was continually studied in another paper [33]. Zhao et al. [35] considered forgetting mechanism and researched rumor spreading on Live Journal.

The major difference between epidemiological models and rumor spreading models is the removal mechanism. During the past decades, various mathematical models for the propagation of a rumor within a population have been developed. Beyond obvious qualitative parallels, there are also important differences between the spread of rumor and diseases. The spread of rumor, unlike a disease, is usually an intentional act on the part of the transmitter and/or the adopter. A core element associated with the rumor always lacks effective verification, and some rumors that take time to identify, such as those involved in the confirmation of the news. One should take active efforts to discern between true and false and decide whether to transmit or not.

In information times, the network in people′s daily life plays an increasingly important role, and people can read information from many sources. Because network information has always suffered from a lack of credibility, people cannot believe it immediately, but are able to believe news from their friends and relatives more easily. Especially, rumors mostly come from network and then spread in real life mouth by mouth. Many rumors come from network and are hidden in the depths of one′s heart for a period of time before he/she becomes a spreader or a stifler in real life. Sometimes, many people would be better to believe that it exists than it does not. Actually, some people would not distinguish uncertain information from right and wrong; their interest is an important factor for deciding whether to spread rumor or not. So the classical rumor transmission model needs to be improved and perfected.

In this paper, we apply a general model, inspired by epidemiology and informed by our knowledge of the sociology of the spread dynamics, to the diffusion of the rumor. The paper deals with the rumor transmission model with incubation and varying total population. We provide a more detailed and realistic description of rumor spreading process with combination of incubation mechanism and the D-K model of rumor. The paper is organized as follows. In the next section, we review the D-K model and introduce a model with homogeneity in susceptibility and transmission. In Section 3, we introduce our general rumor transmission model with incubation and having constant immigration and discuss the existence of equilibrium. In Section 4, we carry out a qualitative analysis of the model. Stability conditions for the rumor-free equilibrium and the endemic equilibrium are derived, respectively. In Section 5, we draw simulations about the model and discuss the implications of these results and, from this, conclude what parameters have impact on each system so that we can come up with suggestions for possible preventative or control methods. Concluding remarks are given in Section 6.

2. Review of Daley-Kendall Framework

Daley and Kendall published a paper aiming to stochastically model the spread of rumors. They considered a closed homogeneously mixing population of N individuals. At any time, an individual can be classified as one of three categories: X(t) denotes those individuals who are ignorant of the rumor; Y(t) Denotes those individuals who are actively spreading the rumor; Z(t) denotes those individuals who know the rumor but have ceased spreading it. For all t, X(t) + Y(t) + Z(t) = N. They referred to these three types of individuals as ignorants, spreaders, and stiflers, respectively [10]. The rumor is propagated through the closed population by contact between ignorants and spreaders, following the law of mass action. They assume that any spreader involved in any pairwise meeting “infects” the “other.” If the “other” is an ignorant, then he/she will become a spreader; if the “other” is a spreader or a stifler, then the spreader(s) will become a stifler(s). A stifler will never, under any circumstances, infect a susceptible because of the definition of a spreader. Stiflers do not transmit the rumor.

Next, Cintron-Arias [36] proposed the following deterministic version of the D-K model:

(2.1)

This model has been extremely useful in the interpretation of the D-K because some analytical analysis can be done on this deterministic version of the model. Still, the D-K model makes some other assumptions. There is no inflow to the susceptible class or outflow from any of the classes. The model also assumes that everybody should be spreader immediately after they learn the rumor, and the process of thinking is virtually ignored. Along these same lines, their model does not take into account the personality of the person who is spreading or receiving the rumor. And finally, it does not allow for people who are “ignorant” to hear the rumor and then choose not to spread it. Still, their model was extremely innovative and is still very useful in the modeling and analysis of rumor spreading.

3. General Rumor Transmission Model with Incubation and Having Constant Immigration

In the following, we will concentrate on the model, based on “homogeneous mixing” with state variables as functions of time, which is more general than the XYZ type model and needs to be studied to investigate the role of incubation in rumor transmission. However, the transmission requires some time for individuals to pass from the infected to the spread state, and we assume that an ignorant individual first goes through a latent period (and is said to become exposed or in the class W) after infected before becoming spreaders or stiflers, and resulting model is of XWYZ type.

We divide the population into four classes: the ignorant class, the incubation class, the spreader class, and the stifler class. Each population densities at time t, respectively, are denoted by X(t), W(t), Y(t), and Z(t), each of which we call rumor class. Those who belong to the ignorant class, whom we call ignorants, do not know about the rumor. Those who belong to the incubation class, whom we call incubators, know about the rumor and require active effort to discern between true and false. In fact, someone would not distinguish uncertain information from right and wrong; their interest is an important factor for deciding whether to spread rumor or not, so incubation class also has infectious force. It is important to note, though, that this infectious force is only valid for the ignorant but not for all, since the incubator is not entirely dissuasive. Over time, someone firmly believes the rumor and becomes spreader, others do not believe it and become stiflers. Those who belong to the spreader class, whom we call spreaders, know about the rumor and spread it actively. Those who belong to the stifler class, whom we call stiflers, know about the rumor and do not spread it. The total population size at time t is denoted by N(t), with N = X + W + Y + Z. We assume that no transition of rumor class happens unless a spreader and incubator contact someone, and there exists infectious force in the latent period and infected period. The transfer diagram is depicted in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The basic scheme of population dynamics models for the spread of rumor.

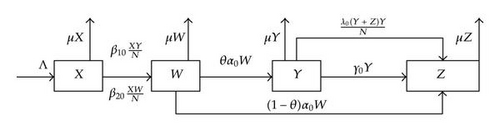
For the meantime, and we assume the rumor is “constant,” that is, the same remark is transmitted at all times. First, we consider the transmission of a constant rumor with variable population size, we assume that the transmission of a constant rumor in a population with constant immigration and emigration. All recruitment is into the ignorant class and occurs at a constant Λ, and the emigration rate is μ. Thus, the maximum value that 1/μ can take is the average lifespan of the rumor within a generation of researchers in the relevant community. We assume that Λ, μ are positive constants, and that emigration is independent of rumor class. When a spreader or incubator contacts an ignorant, the spreader or incubator transmits the rumor at a constant frequency, and the ignorant gets to know about it and requires time to discern between true and false and becomes rumor latent. Then the incubator does not always become a spreader, but may doubt its credibility and consequently become a stifler. And so, we assume that β₁₀XYΔt/N and β₂₀XWΔt/N are ignorants and incubators that change their rumor class and become exposed during the small interval (t, t + Δt), respectively, where β₁₀ and β₂₀ are positive constant numbers representing the product of the contact frequency and the probability of transmitting the rumor. We assume that α₀W incubators change their rumor class and become spreaders at a constant rate θ ∈ (0,1], and others become stiflers at rate 1 − θ, where α₀ is a positive constant number representing the proportion of incubators change their rumor-class. When two spreaders contact with each other, both of them transmit the rumor at a constant frequency. Hearing it again and again, the spreader gets bored, gradually loses interest in it, and consequently becomes a stifler. And so, we assume that λ₀Y²Δt/N spreaders become stiflers during the small interval (t, t + Δt), where λ₀ is a positive constant number. When a spreader contacts a stifler, the spreader transmits the rumor at a constant frequency, and after hearing it, the spreader tries to remove it, because the stifler shows no interest in it or denies it. As a result, the spreader becomes a stifler. And so, we assume that λ₀YZΔt/N spreaders become stiflers during the small interval (t, t + Δt). Any spreader may automatically lose interest in spreading, and it becomes a stifler at rate γ₀.

The model is described by the following system of differential equations:

(3.1)

Since the total population size, N(t) satisfies the equation dN/dt = Λ − μN, and N(t) varies over time and approaches a stable fixed point, Λ/μ, as t → ∞. We can obtain analytical results by considering the limiting system of (3.1) in which the total population is assumed to be constant N = N⁰ = Λ/μ (similar as in [37]). Let x = X/N, y = Y/N, z = Z/N, τ = μt, β₁ = β₁₀/μ, β₂ = β₂₀/μ, α = α₀/μ, λ = λ₀/μ, and γ = γ₀/μ. It is easy to verify that x, w, y, and z satisfy the system of differential equations

(3.2)

subject to the restriction x + w + y + z = 1. Also, we rewrite τ as t, determining z from z = 1 − x − w − y.

Then the reduced limiting dynamical system is given by

(3.3)

Letting the right side of each of the differential equations be equal to zero in system (3.3) gives the equation

(3.4)

The feasible region for (3.4) is

, and we study (3.4) in closed set

(3.5)

where

denotes the nonnegative cone and its lower dimensional faces. It can be verified that A is positively invariant with respect to (3.3). We denote by ∂A and Å the boundary and the interior of A in

, respectively.

Adding the first and second equations of system (3.4), and then substituting it into the last equation of system (3.4), we have

(3.6)

Substituting (3.6) into the second equation of (3.4), w satisfies the following equation:

(3.7)

So the system (3.4) always has the rumor-free equilibrium(RFE) P₀ = (1,0, 0) and unique rumor-endemic equilibrium(REE) P^* = (x^*, w^*, y^*), where w yields

(3.8)

with a = −β₂λα(α + 1); b = β₂λα − (α + 1)[β₁θα + β₂(γ + 1) + λα]; c = [β₁θα + β₂(γ + 1)]−(α + 1)(γ + 1) = (α + 1)(γ + 1)[R₀ − 1], where R₀ = (β₁θα + β₂(γ + 1))/((α + 1)(γ + 1)).

If β₂ > 0, so that (3.8) is quadratic, and if R₀ > 1, then we have c > 0, and there is a unique positive real root of (3.8), and thus, it is a unique rumor-endemic equilibrium. If R₀ ≤ 1, it implies that β₂ ≤ (α + 1) − (β₁θα/(γ + 1)) < (α + 1), then

(3.9)

There is no positive solution for above quadratic (3.8) because the a < 0 and c < 0, which means that the model has no positive equilibrium in this case. These results are summarized below.

(i)
If R₀ ≤ 1, then there is no positive equilibrium.
(ii)
If R₀ > 1, then there is a unique positive equilibrium P^* = (x^*, w^*, y^*).

In the next section, we will study the property of these equilibria and perform a global qualitative analysis of system (3.3).

4. Mathematical Analysis

The reduced limiting dynamical system (3.3) with initial conditions: x(0) = x₀ > 0, w(0) = w₀ > 0, and y(0) = y₀ > 0, and the local stability for both the equilibria are established as follows.

Theorem 4.1. The rumor-free equilibrium (RFE) P₀ is

(i)
locally asymptotically stable if R₀ < 1,
(ii)
unstable (saddle point) if R₀ > 1,
(iii)
a transcritical bifurcation occurs at R₀ = 1.

Proof. The variational matrix of system (3.3) at DFE is given by

(4.1)

The variational matrix leads to the characteristic equation

(4.2)

It follows that one eigenvalue is negative, that is, φ₁ = −1. Clearly, if R₀ < 1 and β₂ < (α + 1) − (β₁θα/(γ + 1)) < (α + γ + 2), then the other two eigenvalues of J(P₀) have negative real parts. If R₀ > 1, then two eigenvalues of J(P₀) have negative real parts, and one eigenvalue has positive real part. Hence, RFE is locally asymptotically stable if R₀ < 1 and unstable (saddle point) if R₀ > 1. The proof is completed for parts (i) and (ii).

Observing that

(4.3)

it follows that the RFE P₀ is locally stable when θ < θ^*, whereas it loses its stability when θ > θ^*. As a consequence, the critical value θ = θ^* is a bifurcation value. Next step is to investigate the nature of the bifurcation involving the rumor-free equilibrium P₀ at θ = θ^* (or equivalently at R₀ = 1).

In the following, we will make use of Theorem A.1, summarized in the appendix, which has been obtained in [38] and is based on the use of the center manifold theory [39]. Theorem A.1 prescribes the role of the coefficients m and n of the normal form representing the system dynamics on the central manifold, in deciding the direction of the transcritical bifurcation occurring at ϕ = 0 (see Appendices A and B and the notation defined therein). More precisely, if m < 0 and n > 0, then the bifurcation is forward.

We apply Theorem A.1 to show that system (3.3) may exhibit a forward bifurcation when θ = θ^*. First of all, observe that the eigenvalues of the matrix

(4.4)

are given by

(4.5)

Thus, φ₃ = 0 is a simple zero eigenvalue, and the other eigenvalues are real and negative. Hence, when θ = θ^* (or equivalently when R₀ = 1), the RFE P₀ is a nonhyperbolic equilibrium: the assumption (I) of Theorem A.1 is then verified.

Now denote by ω = (ω₁, ω₂, ω₃) ^T a right eigenvector associated with the zero eigenvalue φ₃ = 0. It follows

(4.6)

so that

(4.7)

Furthermore, the left eigenvector η = (η₁, η₂, η₃) satisfying η · ω = 1 is given by

(4.8)

so that

(4.9)

The coefficients m and n defined in Theorem A.1,

(4.10)

may be now explicitly computed. Taking into account system (3.3) and considering only the nonzero components of the left eigenvector v, it follows that

(4.11)

where Φ = α²(1 + γ + λ) + α(2 + 2γ + λ − β₂λ) + γ + 1 = (α + 1) ²(γ + 1) + λα(α + 1 − β₂). Since R₀ = 1, β₂ = (α + 1) − (β₁θα/(γ + 1)) < (α + 1), and Φ > 0, then the coefficient n is always positive, and the coefficient m is negative.

Now, by applying Theorem A.1, we may conclude that system (3.3) exhibits a transcritical bifurcation at R₀ = 1.

Theorem 4.2. If R₀ > 1, the rumor-endemic equilibrium (REE) P^* of the system (3.3) is locally asymptotically stable.

Proof. The Jacobian matrix at REE P^* is given by

(4.12)

Its characteristic equation is det (φE − J(P^*)) = 0, where E is the unit matrix and

(4.13)

So the characteristic equation becomes φ³ + C₁φ² + C₂φ + C₃ = 0, where

(4.14)

We have

(4.15)

Since 1 − x^* > 0, then C₁ > 0, C₂ > 0, C₃ > 0, and C₁C₂ − C₃ > 0. Hence, by Routh-Hurwitz criterion, the rumor-endemic equilibrium point P^* is locally asymptotically stable.

We analyze the global stability of the rumor-free and rumor-endemic steady states. Firstly, we consider the global stability of rumor-free equilibrium point. Here, we use the method developed by Castillo-Chavez et al. [40]. Now, we state two conditions which guarantee the global stability of the rumor-free state. Rewrite the model system (3.3) as

(4.16)

where u = (x) and v = (w, y), with u ∈ R denotes the number of uninfected individuals and v ∈ R² denoting (its components) the number of infected individuals including the latent and the infectious. The rumor-free equilibrium is now denoted by P₀ = (u₀, 0). The following conditions (H1) and (H2) must be met to guarantee a local asymptotic stability:

(H1)
for du/dt = F(u, 0), u₀ is globally asymptotically stable;
(H2)
, where , for (u, v) ∈ Ω,

where B = D_ZG(u₀, 0) is an M-matrix (the off-diagonal elements of B are nonnegative), and Ω is the region where the model makes sociological sense. Then, the following lemma holds.

Lemma 4.3. The fixed point P₀ = (u₀, 0) is a globally asymptotic stable equilibrium of (4.16) provided that R₀ < 1 and that assumptions (H1) and (H2) are satisfied.

Theorem 4.4. Suppose R₀ < 1. The rumor-free equilibrium P₀ is globally asymptotically stable.

Proof. let u = (x), v = (w, y), and P₀ = (u₀, 0), where u₀ = 1, then du/dt = F(u, v) = 1 − β₁xy − β₂xw − x. At x = x₀, F(u, 0) = 0 and du/dt = F(u, 0) = 1 − u. As t → ∞, u → u₀. Hence, u = u₀ is globally asymptotically stable.

Now

(4.17)

where

and

Clearly, , and B is an M-matrix; hence, above conditions (H1) and (H2) are satisfied, and hence by Lemma 4.3, the rumor-free equilibrium P₀ is globally asymptotically stable if R₀ < 1.

In the following, using the geometrical approach of Li and Muldowney in [41], we obtain simple sufficient conditions that the rumor-endemic steady state is globally asymptotically stable, we give a brief outline of this geometrical approach in Appendix B.

Theorem 4.5. If R₀ > 1, then the rumor-endemic equilibrium P^* of the system (3.3) is globally stable in Ω.

Proof. From Theorem 4.2, it is clear that R₀ > 1 implies the existence and uniqueness (as an interior equilibrium) of the rumor endemic equilibrium P^*, also P^*, if exists, is locally asymptotically stable. From Theorem 4.1 when R₀ > 1, P₀ is unstable. The instability of P₀, together with P₀ ∈ ∂Ω, implies the uniform persistence, that is, there exists a constant c > 0 such that lim _t→∞inf ξ(t) > c, ξ = (x, w, y).

The uniform persistence, because of boundedness of Ω, is equivalent to the existence of a compact set in the interior of Ω which is absorbing for the system (3.3). Hence, the condition (H3) in Appendix B is satisfied. Now, the second additive compound matrix J^[2](x, w, y) is given by

(4.18)

where

;

We consider the function P = P(x, w, y) = diag {1, w/y, w/y}, so that P_gP⁻¹ = diag {0, (w^′/w) − (y^′/y), (w^′/w) − (y^′/y)}.

Then,

(4.19)

Let

(4.20)

where B₁₁ = β₂x − β₁y − β₂w − α − 2, B₁₂ = [β₁xy/w, β₁xy/w], B₂₁ = [w/y(θα − λy), −λw] ^T,

(4.21)

Now consider the norm in R³ as |(ε₁, ε₂, ε₃) | = max {|ε₁ | , |ε₂ + ε₃|}, where (ε₁, ε₂, ε₃) denotes vector in R³ and denote by ψ the Lozinski measure with respect to this norm. It follows [41] that

(4.22)

where |B₁₂|, |B₂₁| are matrix norms with respect to the L¹ vector norm, and ψ₁ denotes the Lozinski

measure with respect to the L¹ norm.

Then,

(4.23)

Therefore,

(4.24)

Along each solution (x(t), w(t), y(t)) of the system with (x(0), w(0), y(0)) ∈ Q, where Q is the compact absorbing set we have

(4.25)

which implies that

(4.26)

Summarizing Theorems 4.1–4.5, we have the following results on the dynamics of the original system (3.3).

Theorem 4.6. (i) If R₀ < 1, then system (3.3) has a unique rumor-free equilibrium P₀ = (1,0, 0), which is a global attractor in the first octant.

(ii) If R₀ = 1, a transcritical bifurcation occurs at θ = θ^*.

(iii) If R₀ > 1, then system (3.3) has two equilibria, a rumor-free equilibrium (RFE) P₀ = (1,0, 0) and an rumor-endemic equilibrium P^* = (x*, w*, y*). The rumor-endemic equilibrium (REE) P^* is a global attractor in the interior of the first octant.

5. Discussions and Simulations

This paper deals with the rumor transmission model with incubation and varying total population. It concerns rumor with latent period, for example, many rumors come from network and are hidden in the depths of one′s heart for a period of time before he/she becomes a spreader or a stifler in real life. Our main results present the global dynamics of rumor transmission model with incubation and its transformed proportionate system, the process of communication correlations between the two systems in rumor eradication and persistence, and the effects of different management strategies on the rumor control.

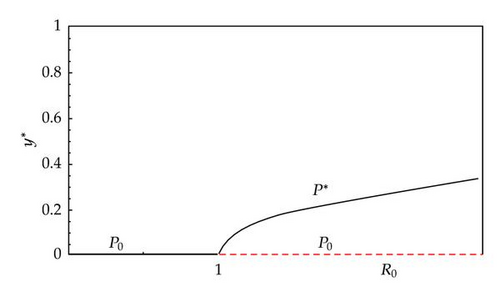
Numerical simulations (parameters and variables used in simulations are summarized in Table 1) carried out for system (3.3) show that the rumor “dies out” when the basic reproduction number R₀ < 1 (the threshold) (Figure 2), and the rumor persists at an “endemic” level when R₀ > 1 (Figure 3). We prove that the transcritical bifurcation occurs at R₀ = 1 (Figure 4) by projecting the flow onto the extended center manifold. Those parameters can be set according to rumors control requirements.

Table 1. Dimension of parameters and variables used in simulations.

Variable or parameter	Dimension	Implication
x, w, y, z	Dimensionless	Proportional population
X, W, Y, Z	Hundred thousand Day⁻¹	Number of Population
Λ	Hundred thousand Day⁻¹	The number of immigration population
β_i0 (i = 1,2)	Unity Day⁻¹	Rumor transmission coefficient
λ₀	Unity Day⁻¹	Rumor stifler coefficient
α₀	Dimensionless	Change rate for exposed
γ₀	Dimensionless	Change rate for spreaders
θ	Dimensionless	Believe and spread rate
μ	Dimensionless	The emigration rate
N	Hundred thousand	Total population

Where x = X/N, y = Y/N, z = Z/N, β = β₀/μ, α = α₀/μ, λ = λ₀/μ, and γ = γ₀/μ.

Rewriting R₀, we have

(5.1)

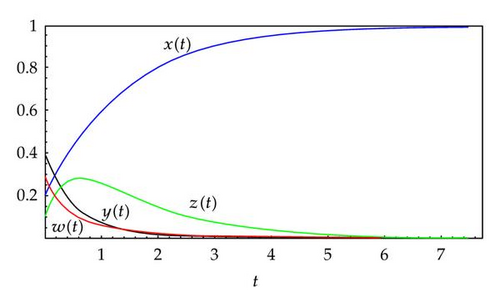
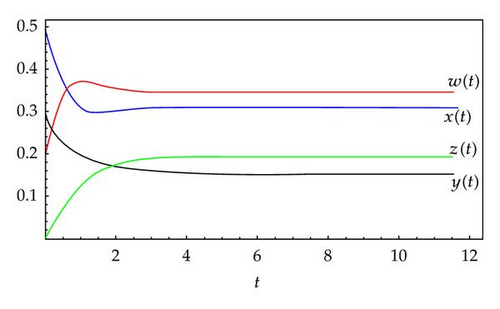
The threshold R₀ is increasing with the rumor transmission coefficient β_i, i = 1,2, the belief, and spread rate θ. If there exist many active members who believe and spread the rumor actively, then β_i, i = 1,2 and θ will be sufficiently large, then R₀ > 1 is easily, and the rumor will persist at an “endemic” level. Conversely, if the managers induct public views and remind the public of not relying on rumors more carefully, increasing the public’s ability to distinguish, then the parameters β_i, i = 1,2, and θ will become smaller and make the threshold R₀ < 1, and the rumor will “die out.”

When the rate of the incubators believe the rumor reaches its critical value

(5.2)

then R₀ = 1. So the condition required to eradicate the rumor from the population is that believe and spread rate (θ) must be lesser than the critical vaccination coverage (θ^*); otherwise, the rumor persists in the population.

Though the number of those who believe the rumor does not depend on θ explicitly, the believe and spread rate of the rumor is proportional to the “endemic” level of rumor. The effect of θ on the size of infected class is shown in Figure 5 for constant of other parameters. Numerical simulations indicate that the steady-state value y^* of the rumor infectives increases as θ increases (see Figure 5).

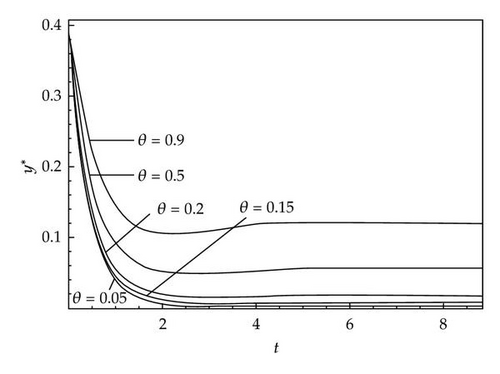
Actually, R₀ is an increasing function of the parameter β₂ and β₁. Thus, it is necessary and important for emergency management to control the rumor by decreasing the transmission force β_i, i = 1,2, and make R₀ less than one, with the aggressive control measures and policies, such as improving the ability of the signature verification for rumors and enhancing the transparency of the information in an emergency event, then the rumor transmission can be effectively controlled. Sometimes information disclosure can achieve management aims for rumor transmission more effectively and at far lower cost than traditional regulation.

If β₂ = 0, people could not spread the rumor before becoming spreaders or stiflers, it means that one should try to find out the truth of the matter and decide to believe the rumor or not. Actually, in that case, , and this means it is easier to make the threshold less that one, then the rumor will “die out” faster.

In the special cases when the population size remains constant (i.e., Λ = 0, and μ = 0), the latent period is negligible, and the model (3.1) reduces to a D-K rumor model with bilinear incidence.

6. Concluding Remarks

In the paper, a deterministic model for the transmission dynamics of rumor is developed and analyzed. We discuss the XWYZ model with constant immigration and incubation; this analysis results meet the actual circs better, more external, and easier to be understood. We derive a basic reproduction number R₀ and that it determines the global dynamics of system (3.3); if R₀ < 1, the rumor-free equilibrium(RFE) P₀ is globally asymptotically stable in A, and rumor can be eradicated; if R₀ > 1, a unique rumor endemic equilibrium (REE) P^* is globally asymptotically stable in the interior of the feasible region so that the rumor persists at the rumor endemic equilibrium level if it is initially present. As the bifurcation diagram (see Figure 4) shows, the occurrence of transcritical bifurcation (forward) has important consequences from the point of view of rumor control and thus for the eradication of the rumor. When the bifurcation parameter R₀ crosses the bifurcation threshold R₀ = 1, a rumor-endemic equilibrium enters the positive orthant. Since the “endemic” level at the equilibrium is a continuous function of R₀, as a consequence for successfully eradication of the rumor, one should simply reduce R₀ continuously below the threshold value 1.

Since some rumors spread in a certain group of people; we then can assume that the transmission coefficient is a function of parameters for special populations and time, which may take the nonautonomous system instead of the autonomous system, we leave this for the future work.

Acknowledgments

This work was partially supported by the National Natural Science Foundation of China (Nos. 70732003, 71071102) and the Construction of the Innovating Ability for Graduate (Z-120-016). The authors are very grateful to the anonymous referees for their valuable comments and suggestions that helped us improve the quality of this paper.

Appendices

A.

Theorem A.1. Let us consider a general system of ODEs with a parameter ϑ

(A.1)

Without loss of generality, we assume that ϑ = 0 is an equilibrium for (A.1).

Assume that

(I)
A = D_xf(0,0) is the linearization matrix of system (A.1) around the equilibrium x = 0 with ϑ = 0 evaluated at 0. Zero is a simple eigenvalue of A and all other eigenvalues of A have negative real parts;
(II)
matrix A has a (nonnegative) right eigenvector u and a left eigenvector v corresponding to the zero eigenvalue. Let f_k denote the kth component of f and
(A.2)
then the local dynamics of system (A.1) around x = 0 are totally determined by m and n:
(i)
m > 0, n > 0. When ϑ < 0, with |ϑ | ≪ 1, x = 0 is locally asymptotically stable, and there exists a positive unstable equilibrium; when 0 < ϑ ≪ 1, x = 0 is unstable, and there exists a negative and locally asymptotically stable equilibrium;
(ii)
m < 0, n < 0. When ϑ < 0, with |ϑ| ≪ 1, x = 0 is unstable; when 0 < ϑ ≪ 1, x = 0 is locally asymptotically stable, and there exists a positive unstable equilibrium;
(iii)
m > 0, n < 0. When ϑ < 0, with |ϑ| ≪ 1, x = 0 is unstable and there exists a locally asymptotically stable negative equilibrium; when 0 < ϑ ≪ 1, x = 0 is stable and a positive unstable equilibrium appears;
(iv)
m < 0, n > 0. When ϑ < 0 changes from negative to positive, x = 0 changes its stability from stable to unstable. Correspondently, a negative unstable equilibrium becomes positive and locally asymptotically stable.

Proof. See [38].

B.

Consider the autonomous dynamical system

(B.1)

where g : D → Rⁿ, D ⊂ Rⁿ open set and simply connected and g ∈ C¹(D). Denote by ξ(t, ξ₀) the solution to (B.1) such that ξ(0, ξ₀) = ξ₀. Let ξ^* be an equilibrium of (B.1), that is, g(ξ^*) = 0. Assume that the following hypotheses hold:

(H3)
there exists a compact absorbing set K ⊂ D,
(H4)
equation (B.1) has a unique equilibrium ξ^* in D.

We recall that ξ^* is said to be globally stable in D if it is locally stable, and all trajectories in D converge to ξ^*. For n ≥ 2, by a Bendixson criterion, we mean a condition satisfied by g which precludes the existence of nonconstant periodic solutions of (B.1). The classical Bendixson′s condition div g(ξ) < 0 for n = 2 is robust under C¹ local perturbations of g(ξ). For higher-dimensional systems, the C¹ robust properties are discussed in [41].

A point ξ₀ ∈ D is wandering for (B.1) if there exists a neighborhood U of ξ₀ and T > 0 such that U∩ξ(t, U) is empty for all t > T. Thus, for example, all equilibria and limit points are nonwandering. The following global-stability principle is established in Li and Muldowney [41] for autonomous systems in any finite dimension.

Lemma B.1. Suppose that assumptions (H3) and (H4) hold. Assume that (B.1) satisfies a Bendixson criterion that is robust under C¹ local perturbations of g(ξ) at all nonequilibrium nonwandering points for (B.1), then ξ^* is globally stable in D provided it is stable.

The following Bendixson criterion is given in [41] and shown to have the robustness required by Lemma B.1. Let P(ξ) be a

matrix-valued function that is C¹ on D. Assume that P⁻¹ exists and is continuous for ξ ∈ K, the compact absorbing set. A quantity

is defined as

(B.2)

where B = P_gP⁻¹ + PJ^[2]P⁻¹, the matrix P_g is (P_ij(ξ)) _g = (∂P_ij(ξ)/∂x) ^T · g(ξ) = ∇P_ijg(ξ) and the matrix J^[2] is the second additive compound matrix of the Jacobian matrix J, that is, J(ξ) = Dg(ξ). Let ψ(B) be the Lozinski

measure of B with respect to a vector norm |·| in R^N,

defined by

(B.3)

It is shown in [41] that, if D is simply connected, the condition rules out the presence of any orbit that gives rise to a simple closed rectifiable curve that is invariant for (B.1), such as periodic orbits, homoclinic orbits, and heteroclinic cycles. Moreover, it is robust under C¹ local perturbations of g(ξ) near any nonequilibrium point that is nonwandering. In particular, the following global-stability result is proved in Li and Muldowney [41].

Lemma B.2. Assume that D is simply connected and that the assumptions (H3) and (H4) hold. Then the unique equilibrium ξ^* of (B.1) is globally stable in D if .

References

1 Hayakawa H., Sociology of Rumor-Approach from Formal Sociology, 2002, Seikyusya, Tokyo, Japan.
Google Scholar
2 Shibutani T., Improvised News: A Sociological Study of Rumor, 1966, Bobbs-Merrill, Indianapolis, Ind, USA.
Google Scholar
3 Kosfeld M., Rumours and markets, Journal of Mathematical Economics. (2005) 41, no. 6, 646–664, https://doi.org/10.1016/j.jmateco.2004.05.001, 2156368, ZBL1135.91386.
10.1016/j.jmateco.2004.05.001
Web of Science® Google Scholar
4 Rapoport A., Spread of information through a population with socio-structural bias. I. Assumption of transitivity, 1953, 15, 523–533, 0058955.
Google Scholar
5 Rapoport A., Spread of information through a population with socio-structural bias. II. Various models with partial transitivity, 1953, 15, 535–546, 0058956.
Google Scholar
6 Rapoport A. and Rebhun L. I., On the mathematical theory of rumor spread, The Bulletin of Mathematical Biophysics. (1952) 14, 375–383, 0052085.
10.1007/BF02477853
Google Scholar
7 Dietz K., Epidemics and rumours: a survey, Journal of the Royal Statistical Society A. (1967) 130, no. 4, 505–528, 0223059, https://doi.org/10.2307/2982521.
10.2307/2982521
Web of Science® Google Scholar
8 Daley D. J. and Gani J., Epidemic modelling: An Introduction, 1999, 15, Cambridge University Press, Cambridge, Cambridge Studies in Mathematical Biology, https://doi.org/10.1017/CBO9780511608834, 1688203.
10.1017/CBO9780511608834
Google Scholar
9 Bettencourt L. M. A., Cintrón-Arias A., Kaiser D. I., and Castillo-Chávez C., The power of a good idea: quantitative modeling of the spread of ideas from epidemiological models, Physica A. (2006) 364, 513–536, 2-s2.0-33645136546, https://doi.org/10.1016/j.physa.2005.08.083.
10.1016/j.physa.2005.08.083
Web of Science® Google Scholar
10 Daley D. J. and Kendall D. G., Stochastic rumours, Journal of the Institute of Mathematics and its Applications. (1965) 1, 42–55, 0182064, https://doi.org/10.1093/imamat/1.1.42.
10.1093/imamat/1.1.42
Google Scholar
11 Maki D. P. and Thompson M., Mathematical Models and Applications, with Emphasis on Social, Life, and Management Sciences, 1973, Prentice-Hall, Englewood Cliffs, NJ, USA, 0366359.
Google Scholar
12 Daley D. J., Gani J. et al., Epidemic Modelling, 2000, Cambridge University Press, Cambridge, UK.
Google Scholar
13 Belen S., Kropa E., and Weber G. W., Rumours within time dependent Maki-Thompson Model, Working paper, 2008.
Google Scholar
14 Huang W., On Rumour Spreading with Skepticism and Denia, Working paper, 2011.
Google Scholar
15 Lefèvre C. and Picard P., Distribution of the final extent of a rumour process, Journal of Applied Probability. (1994) 31, no. 1, 244–249, 1260586, https://doi.org/10.2307/3215250, ZBL0796.60098.
10.2307/3215250
Web of Science® Google Scholar
16 Pittel B., On a Daley-Kendall model of random rumours, Journal of Applied Probability. (1990) 27, no. 1, 14–27, 1039181, https://doi.org/10.2307/3214592, ZBL0698.60061.
10.2307/3214592
Web of Science® Google Scholar
17 Thompson K., Estrada R. Castro, Daugherty D., and Arias A. Cintrn, A deterministic approach to the spread of rumors, Working paper, 2003, Washington, DC, USA.
Google Scholar
18 Kawachi K., Deterministic models for rumor transmission, Nonlinear Analysis. (2008) 9, no. 5, 1989–2028, https://doi.org/10.1016/j.nonrwa.2007.06.004, 2441764, ZBL1156.91460.
10.1016/j.nonrwa.2007.06.004
Google Scholar
19 Kawachi K., Seki M., Yoshida H., Otake Y., Warashina K., and Ueda H., A rumor transmission model with various contact interactions, Journal of Theoretical Biology. (2008) 253, no. 1, 55–60, 2-s2.0-44749085103, https://doi.org/10.1016/j.jtbi.2007.11.024.
10.1016/j.jtbi.2007.11.024
PubMed Web of Science® Google Scholar
20 Lebensztayn E. and Machado F. P., Limit theorems for a general stochastic rumour model, ARXIV. (2010) .
Google Scholar
21 Pearce C. E. M., The exact solution of the general stochastic rumour, Mathematical and Computer Modelling. (2000) 31, no. 10–12, 289–298, Stochastic models in engineering, technology, and management (Gold Coast, 1996)https://doi.org/10.1016/S0895-7177(00)00098-4, 1768764, ZBL1043.92526.
10.1016/S0895-7177(00)00098-4
Google Scholar
22 Gani J., The Maki-Thompson rumour model: a detailed analysis, Environmental Modelling and Software. (2000) 15, no. 8, 721–725, 2-s2.0-0034351078, https://doi.org/10.1016/S1364-8152(00)00029-3.
10.1016/S1364-8152(00)00029-3
Web of Science® Google Scholar
23 Dickinson R. E. and Pearce C. E. M., Rumours, epidemics, and processes of mass action: synthesis and analysis, Mathematical and Computer Modelling. (2003) 38, no. 11–13, 1157–1167, https://doi.org/10.1016/S0895-7177(03)90116-6, 2028298, ZBL1048.60083.
10.1016/S0895-7177(03)90116-6
Google Scholar
24 Zanette D. H., Dynamics of rumor propagation on small-world networks, Physical Review E. (2002) 65, no. 4, 2-s2.0-41349109719, https://doi.org/10.1103/PhysRevE.65.041908, 041908.
10.1103/PhysRevE.65.041908
CAS PubMed Web of Science® Google Scholar
25 Nekovee M., Moreno Y., Bianconi G., and Marsili M., Theory of rumour spreading in complex social networks, Physica A. (2007) 374, no. 1, 457–470, 2-s2.0-33751310571, https://doi.org/10.1016/j.physa.2006.07.017.
10.1016/j.physa.2006.07.017
Web of Science® Google Scholar
26 Isham V., Harden S., and Nekovee M., Stochastic epidemics and rumours on finite random networks, Physica A. (2010) 389, no. 3, 561–576, 2-s2.0-70350746051, https://doi.org/10.1016/j.physa.2009.10.001.
10.1016/j.physa.2009.10.001
Web of Science® Google Scholar
27 Sudbury A., The proportion of the population never hearing a rumour, Journal of Applied Probability. (1985) 22, no. 2, 443–446, 789367, https://doi.org/10.2307/3213787, ZBL0578.92025.
10.2307/3213787
Web of Science® Google Scholar
28 Zanette D. H., Critical behavior of propagation on small-world networks, Physical Review E. (2001) 64, no. 5, 050901, 2-s2.0-0035510399.
10.1103/PhysRevE.64.050901
CAS PubMed Web of Science® Google Scholar
29 Berenbrink P., Elsässer R., and Sauerwald T., M. de Berg, U. Meyer et al., Communication complexity of quasirandom rumor spreading, Algorithms—ESA 2010, 2010, Springer, Berlin, Germany, 134–145, 2762849, https://doi.org/10.1007/978-3-642-15775-2_12.
10.1007/978-3-642-15775-2_12
Google Scholar
30 Sauerwald T., Stauery A. et al., Rumor spreading and vertex expansion on regular graphs, Proceedings of the 22nd ACM-SIAM Symposium, January 2011, San Francisco, Calif, USA, 462–475.
Google Scholar
31 Buzna L., Peters K., and Helbing D., Modelling the dynamics of disaster spreading in networks, Physica A. (2006) 363, no. 1, 132–140, 2-s2.0-33645158226, https://doi.org/10.1016/j.physa.2006.01.059.
10.1016/j.physa.2006.01.059
Web of Science® Google Scholar
32 Liu Z., Lai Y. C., and Ye N., Propagation and immunization of infection on general networks with both homogeneous and heterogeneous components, Physical Review E. (2003) 67, no. 3, 2-s2.0-42749102826, 031911.
10.1103/PhysRevE.67.031911
CAS PubMed Web of Science® Google Scholar
33 Zhou J., Liu Z., and Li B., Influence of network structure on rumor propagation, Physics Letters A. (2007) 368, no. 6, 458–463, 2-s2.0-34548031635, https://doi.org/10.1016/j.physleta.2007.01.094.
10.1016/j.physleta.2007.01.094
CAS Web of Science® Google Scholar
34 Moreno Y., Nekovee M., and Pacheco A. F., Dynamics of rumor spreading in complex networks, Physical Review E. (2004) 69, no. 6, 2-s2.0-42749098327, https://doi.org/10.1103/PhysRevE.69.066130, 066130.
10.1103/PhysRevE.69.066130
CAS PubMed Web of Science® Google Scholar
35 Zhao L., Wang Q., [email protected], Cheng J., Chen Y., Wang J., and Huang W., Rumor spreading model with consideration of forgetting mechanism: a case of online blogging LiveJournal, Physica A. (2011) 390, no. 13, 2619–2625, https://doi.org/10.1016/j.physa.2011.03.010.
10.1016/j.physa.2011.03.010
Web of Science® Google Scholar
36 Cintron-Arias A., Modeling and parameter estimation of contact processes, Ph.D. thesis, 2006, Cornell University.
Google Scholar
37 Mischaikow K., Smith H., and Thieme H. R., Asymptotically autonomous semiflows: chain recurrence and Lyapunov functions, Transactions of the American Mathematical Society. (1995) 347, no. 5, 1669–1685, https://doi.org/10.2307/2154964, 1290727, ZBL0829.34037.
10.1090/S0002-9947-1995-1290727-7
Web of Science® Google Scholar
38 Castillo-Chavez C. and Song B., Dynamical models of tuberculosis and their applications, Mathematical Biosciences and Engineering. (2004) 1, no. 2, 361–404, https://doi.org/10.3934/mbe.2004.1.361, 2130673, ZBL1060.92041.
10.3934/mbe.2004.1.361
PubMed Web of Science® Google Scholar
39 Guckenheimer J. and Holmes P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 1983, 42, Springer, Berlin, Germany, 709768.
10.1007/978-1-4612-1140-2
Google Scholar
40 Castillo-Chavez C., Feng Z., and Huang W., Mathematical Approaches for Emerging and Re-Emerging Infectious Diseases: An Introduction, 2002, 125, Springer, New York, NY, USA, 229–250, 1938888, ZBL1021.92032.
10.1007/978-1-4757-3667-0_13
Google Scholar
41 Li M. Y. and Muldowney J. S., A geometric approach to global-stability problems, SIAM Journal on Mathematical Analysis. (1996) 27, no. 4, 1070–1083, https://doi.org/10.1137/S0036141094266449, 1393426, ZBL0873.34041.
10.1137/S0036141094266449
Web of Science® Google Scholar

Citing Literature

All articles

Analyzing the Dynamics of a Rumor Transmission Model with Incubation

Abstract

1. Introduction

2. Review of Daley-Kendall Framework

3. General Rumor Transmission Model with Incubation and Having Constant Immigration

4. Mathematical Analysis

5. Discussions and Simulations

6. Concluding Remarks

Acknowledgments

Appendices

A.

B.

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analyzing the Dynamics of a Rumor Transmission Model with Incubation

Abstract

1. Introduction

2. Review of Daley-Kendall Framework

3. General Rumor Transmission Model with Incubation and Having Constant Immigration

4. Mathematical Analysis

5. Discussions and Simulations

6. Concluding Remarks

Acknowledgments

Appendices

A.

B.

References

Citing Literature

Figures

References

Related

Information