Journal of Applied Mathematics
Volume 2012, Issue 1 308410
Research Article
Open Access

Numerical Analysis of a Linear-Implicit Average Scheme for Generalized Benjamin-Bona-Mahony-Burgers Equation

Hai-tao Che, 

Corresponding Author

Hai-tao Che

School of Management Science, Qufu Normal University, Rizhao 276800, China qfnu.edu.cn

School of Mathematics and Information Science, Weifang University, Weifang 261061, China wfu.edu.cn

Search for more papers by this author
Xin-tian Pan, 

Xin-tian Pan

School of Mathematics and Information Science, Weifang University, Weifang 261061, China wfu.edu.cn

Search for more papers by this author
Lu-ming Zhang, 

Lu-ming Zhang

Department of Mathematics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China nuaa.edu.cn

Search for more papers by this author
Yi-ju Wang, 

Yi-ju Wang

School of Management Science, Qufu Normal University, Rizhao 276800, China qfnu.edu.cn

Search for more papers by this author
First published: 05 March 2012
https://doi.org/10.1155/2012/308410
Citations: 7
Academic Editor: Yuantong Gu

Abstract

A linear-implicit finite difference scheme is given for the initial-boundary problem of GBBM-Burgers equation, which is convergent and unconditionally stable. The unique solvability of numerical solutions is shown. A priori estimate and second-order convergence of the finite difference approximate solution are discussed using energy method. Numerical results demonstrate that the scheme is efficient and accurate.

1. Introduction

The generalized Benjamin-Bona-Mahony-Burgers (GBBM-Burgers) equation is in the form [1]
()
where α > 0,   β are constants, p ≥ 1 is an integer, and u(x, t) represents the velocity of fluid in the horizontal direction x. When p = 1, (1.1) is called as the Benjamin-Bona-Mahony-Burgers (BBM-Burgers) equation. In the special case, when α = 0, (1.1) is described as the generalized Benjamin-Bona-Mahony equation
()
The Equation (1.2) which is usually called as the generalized regularized long-wave equation proposed by Peregrine [2] and Benjamin et al. [3], so-called generalized Benjamin-Bona-Mahony equation, has been studied by many authors [4–7]. This equation features a balance between the nonlinear dispersive effect but takes no account of dissipation.

In recent years, a vast amount of work and computation has been devoted to the initial value problem for the GBBM-Burgers equation. In [1], Al-Khaled et al. studied the GBBM-Burgers by Decomposition method. In [8], Hayashi et al. investigated large time asymptotics of solutions to the BBM-Burgers equation. In [9], Jiang and Xu investigated the asymptotic behavior of solutions of the initial-boundary value problem for the GBBM-Burgers equations. In [10], Yin et al. studied the large time behavior of traveling wave solutions to the Cauchy problem of the GBBM-Burgers equations. In [11], Mei studied the large time behavior of global solutions to the Cauchy problem of GBBM-Burgers equations. In [12], Kondo and Webler studied the global existence of solutions for multidimensional GBBM-Burgers equations. Kinami et al. discussed the Cauchy problem of the GBBM-Burgers equations by Fourier transform method and energy method [13]. However, there are few studies on finite difference approximations for (1.1) which we consider in this paper.

In a recent work [14], we have made some preliminary computation by proposing a linearized difference scheme for GRLW equation which is unconditionally stable and reduces the computational work, and the numerical results are encouraging. In this paper, we continue our work and propose a linear-implicit difference scheme for generalized BBM-Burgers equation which is unconditionally stable and second-order convergent.

In this paper, we consider the following initial-boundary value problem of the GBBM-Burgers equation
()
An outline of the paper is as follows. In Section 2, we describe a linear-implicit finite difference scheme for the GBBM-Burgers equation and prove the error estimates of 2 order. In Section 3, we show that the scheme is uniquely solvable. In Section 4, convergence and stability of the scheme are proved. In Section 5, numerical results are provided to test the theoretical results.

2. Finite Difference Scheme and Estimate for the Difference Solution

As usual, the following notations will be used:
()
where h = (xR − xL)/J and τ are the uniform spatial and temporal step sizes, respectively,
()
Let denote the approximation of u(xj, tn), . In this paper, we will denote C as a generic constant independent of step sizes h and τ.
We propose a three-level linear-implicit difference scheme for the solution of the problem (1.3)
()
()
()
()
For convenience, the last term of (2.3) is defined by
()

Lemma 2.1 (see [15].)For any two mesh functions , one has

()

Lemma 2.2. For any mesh function , one has

()

Proof. For , one has

()

Lemma 2.3 (Discrete Sobolev Inequality [16]). For any discrete function uh and for any given ε > 0, there exists a constant K(ε, n), depending only ε and n, such that

()

Theorem 2.4. Assume , then there is the estimation for the solution of difference scheme (2.3)–(2.6),

()

Proof. Computing the inner product of (2.3) with (i.e., un+1 + un−1), we obtain

()
Now, computing the fourth term of the left-hand side in (2.13), we have
()
According to Lemmas 2.1 and 2.2, and using (2.14), we get
()
We let
()
It follows from (2.15) that
()
Then we have
()
Using (2.18), we obtain
()
Equation (2.19) yields
()
Using Lemma 2.3, the proof of Theorem 2.4 is completed.

Remark 2.5. Theorem 2.4 implies that scheme (2.3)–(2.6) is unconditionally stable.

3. Solvability

Next, we will discuss the solvability of the scheme (2.3) based on the technique of Omrani et al. [17].

Theorem 3.1. The finite difference scheme (2.3) is uniquely solvable.

Proof. It is obvious that u0 and u1 are uniquely determined by (2.4)-(2.5). Now suppose u0,   u1,    … , un  (1 ≤ n ≤ N − 1) be solved uniquely. Considering the equation of (2.3) for un+1, we have

()
Computing the inner product of (3.1) with un+1, we have
()
where .

In view of difference properties and the boundary conditions (2.6), we obtain

()
It follows from (3.2) and (3.3) that
()
Noting that α > 0 and following from (3.4), we have
()
That is (3.1) has only a trivial solution. Therefore, the scheme (2.3) determines uniquely. This completes the proof.

Remark 3.2. All results above in this paper are correct for IBV problem of the BBM-Burgers equation with finite or infinite boundary.

4. Convergence and Stability of the Difference Scheme

First, we consider the truncation error of the difference scheme (2.3)–(2.6).

Suppose . Making use of Taylor expansion, we find
()
where and ri are the truncation errors of the difference scheme (2.3)–(2.6). It can be easily obtained that (see [18, 19])
()
()

Lemma 4.1. Assume u(x, t) is smooth enough, then the local truncation error of the finite difference scheme (2.3)–(2.6) is

()

Lemma 4.2 (see [16].)Suppose that the discrete function wh satisfies recurrence formula

()
where A, B, Cn  (n = 1, ⋯N) are nonnegative constants. Then
()
where τ is small, such that (A + B)τ ≤ ((N − 1)/2N)(N > 1).

Theorem 4.3. Assume and u ∈ C(4,3), then the solution of the difference scheme (2.3)–(2.6) converges to the solution of the problem (1.3) with order O(h2 + τ2) by the ||·||∞ norm.

Proof. Let . Subtracting (2.3)-(2.5) from (4.1)–(4.3), respectively, we have

()
For a simple notation, the last two terms of (4.7) are defined by
()
Computing the inner product of (4.7) with en+1 + en−1 (i.e., ), we get
()
Similarly to the proof of Theorem 2.4, we obtain
()
According to Theorem 2.4, we obtain
()
In addition, there exists obviously that
()
Substituting (4.10)–(4.12) into (4.9), we have
()
Let
()
Then (4.13) can be rewritten as
()
By Lemma 4.2, it can immediately be obtained that
()
To complete the proof, it is enough to find B0 estimate. From (4.7), we obtain
()
Using (4.3) and (4.8), we get
()
It follows from (4.17) and (4.18) that
()
Thus
()
According to Lemma 2.3, there exists that
()

Similarly, the following theorem can be proved.

Theorem 4.4. Under the conditions of Theorem 4.3, the solution of finite difference scheme (2.3)–(2.6) is stable by the ||·||∞ norm.

5. Numerical Experiments

In this section, we will compute several numerical experiments to verify the correction of our theoretical analysis in the above sections.

Example 5.1 (see [20].)Consider the following initial-boundary problem of BBM-Burgers equation:

()
()
()
We denote the scheme proposed in [20] as Scheme I and the scheme (2.3) in present paper as Scheme II. In computations, we choose the initial condition u0(x) = exp (−x2) [20]. The maximal errors of both schemes are listed in Table 1. We get that a second-order linear scheme is as accurate as Scheme I which is a nonlinear one.

Table 1. The maximal errors of numerical solutions at t = 10 with τ = 0.1 for α = 0.5 when p = 1.
h = 1/4   h = 1/8 h = 1/16 h = 1/32
Scheme I 2.486233e − 4 6.519728e − 5 1.618990e − 5 4.929413e − 6
Scheme II 2.438693e − 4 6.418263e − 5 1.594145e − 5 3.867502e − 6

Example 5.2 (see [13].)Consider the GBBM-Burgers equation

()
with an initial condition
()
and boundary conditions
()
In computations, we choose the initial condition u0(x) = 1/(1 + x4) [13]. Without loss of generality, We take p = 2,4, 8 and α = 0.5, β = 1. Since we do not know the exact solution of (5.4)–(5.6), an error estimate method in [21] is used. A comparison between the numerical solutions on a coarse mesh and those on a refine mesh is made. In order to obtain the error estimates, we consider the solution on mesh h = 1/160 as reference solution and obtain error estimates on mesh h =   1/4,  1/8,  1/16, and 1/32, respectively. We denote the scheme proposed in [13] as Scheme III and make a comparison with the scheme (2.3) in present paper as Scheme II when p = 4 in Table 2. The corresponding errors in the sense of L∞-norm and L2-norm are listed in Tables 3, 4, and 5, respectively. These three tables verify the second-order convergence and good stability of the numerical solutions.

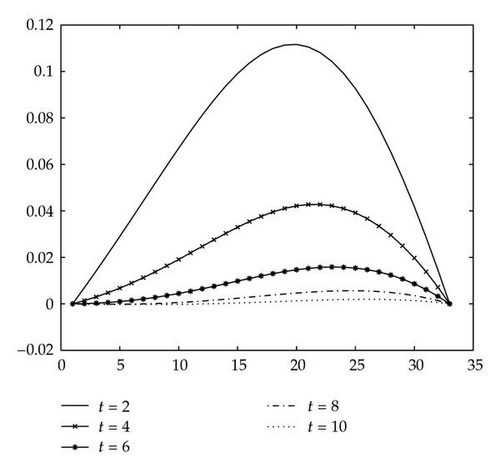
Figures 1 and 2 plot the numerical solutions computed by the linearly implicit scheme (2.3) with τ = 0.1, h = 0.03125, and α = 0.5 when p = 2, 8 at t = 2,4, 6,8, and 10, respectively. From Figures 1 and 2, it is easy to observe that the height of the numerical approximation to u is more and more low with time elapsing due to the effect of dissipative term αuxx. Both of them simulates that the continuous energy E(t) of the problem (1.3) in Theorem 2.4 decreases in time. Numerical experiments show our scheme is accurate and efficient.

Table 2. The maximal errors of numerical solutions at t = 10 with τ = 0.1 for α = 0.5 when p = 4.
h = 1/4   h = 1/8 h = 1/16 h = 1/32
Scheme II 5.293584e − 4 1.416254e − 4 3.480022e − 5 8.423768e − 6
Scheme III 5.069513e − 3 3.444478e − 3 1.916013e − 3 9.262223e − 4
Table 3. The errors of numerical solutions at t = 10 with τ = 0.1 when p = 2.
h   | | vn − un|| | | vn − un | |∞ | | vn/4 − un/4||/| | vn − un|| | | vn/4 − un/4 | |∞/| | vn − un | |∞
0.25 6.377969e − 4 9.352639e − 4 — —
0.125 1.582597e − 4 2.314686e − 4 4.030065 4.040566
0.0625 3.920742e − 5 5.893641e − 5 4.036473 3.927429
0.03125 9.501117e − 6 1.428261e − 5 4.126612 4.126445
Table 4. The errors of numerical solutions at t = 10 with τ = 0.1 when p = 4.
h   | | vn − un|| | | vn − un | |∞ | | vn/4 − un/4||/| | vn − un|| | | vn/4 − un/4 | |∞/| | vn − un | |∞
0.25 6.316492e − 4 9.262624e − 4 — —
0.125 1.568213e − 4 2.294480e − 4 4.027828 4.036916
0.0625 3.885715e − 5 5.828155e − 5 4.035841 3.936889
0.03125 9.416614e − 6 1.412454e − 5 4.126446 4.126262
Table 5. The errors of numerical solutions at t = 10 with τ = 0.1 when p = 8.
h   | | vn − un|| | | vn − un | |∞ | | vn/4 − un/4||/| | vn − un|| | | vn/4 − un/4 | |∞/| | vn − un | |∞
0.25 1.150448e − 4 1.822979e − 4 — —
0.125 2.981547e − 5 4.674950e − 5 3.858561 3.899462
0.0625 7.426232e − 6 1.167644e − 5 4.014885 4.003745
0.03125 1.801424e − 6 2.879611e − 6 4.122423 4.054867
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Numerical solution of u(x, t) with h = 0.03125, τ = 0.1 when p = 2.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Numerical solution of u(x, t) with h = 0.03125, τ = 0.1 when p = 8.

6. Conclusions

In this paper, we have presented a three-level linear-implicit finite difference scheme for the GBBM-Burgers equation, which has a wide range of applications in physics. The convergence and stability as well as second-order error estimate of the finite difference approximate solutions were discussed in detail. Numerical experiments show our scheme is accurate and efficient.

Acknowledgments

This work is supported by the fund of National Natural Science (11171193, 11171180, and 10901096) and the fund of Natural Science of Shandong Province (ZR2009AL019, ZR2011AM016), and the Youth Research Foundation of WFU (no. 2011Z17). The authors thank the referees for their valuable comments.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.