Volume 2012, Issue 1 282367

Research Article

Open Access

Generalization of the Analytical Exponential Model for Homogeneous Reactor Kinetics Equations

Abdallah A. Nahla,

Corresponding Author

Abdallah A. Nahla

[email protected]

Department of Mathematics, Faculty of Science, Tanta University, Tanta 31527, Egypt tanta.edu.eg

Department of Mathematics, Faculty of Science, Taif University, Taif 888, Saudi Arabia tu.edu.sa

Search for more papers by this author

Mohammed F. Al-Ghamdi,

Mohammed F. Al-Ghamdi

Department of Mathematics, Faculty of Science, Taif University, Taif 888, Saudi Arabia tu.edu.sa

Search for more papers by this author

Abdallah A. Nahla,

Corresponding Author

Abdallah A. Nahla

[email protected]

Department of Mathematics, Faculty of Science, Tanta University, Tanta 31527, Egypt tanta.edu.eg

Department of Mathematics, Faculty of Science, Taif University, Taif 888, Saudi Arabia tu.edu.sa

Search for more papers by this author

Mohammed F. Al-Ghamdi,

Mohammed F. Al-Ghamdi

Department of Mathematics, Faculty of Science, Taif University, Taif 888, Saudi Arabia tu.edu.sa

Search for more papers by this author

First published: 16 May 2012

https://doi.org/10.1155/2012/282367

Citations: 7

Academic Editor: Pablo González-Vera

Share a link

Email
Wechat
Bluesky

Abstract

Mathematical form for two energy groups of three-dimensional homogeneous reactor kinetics equations and average one group of the precursor concentration of delayed neutrons is presented. This mathematical form is called “two energy groups of the point kinetics equations.” We rewrite two energy groups of the point kinetics equations in the matrix form. Generalization of the analytical exponential model (GAEM) is developed for solving two energy groups of the point kinetics equations. The GAEM is based on the eigenvalues and the corresponding eigenvectors of the coefficient matrix. The eigenvalues of the coefficient matrix are calculated numerically using visual FORTRAN code, based on Laguerre’s method, to calculate the roots of an algebraic equation with real coefficients. The eigenvectors of the coefficient matrix are calculated analytically. The results of the GAEM are compared with the traditional methods. These comparisons substantiate the accuracy of the results of the GAEM. In addition, the GAEM is faster than the traditional methods.

1. Introduction

In real nuclear reactor problems that involve safety considerations, the coefficients of the space-time neutron diffusion equations depend upon the neutron flux density, precursor concentration of delayed neutrons groups, space, time, and temperature feedback. The numerical methods and the analytical approximations for solving the space-time neutron diffusion equations in the nuclear reactor have been of interest in nuclear physics and reactor design.

Three-dimensional nodal mixed dual method was used for the nuclear reactor kinetics equations with improved quasistatic model and the semiimplicit scheme to solve the precursor equations [1]. A rigorous weight function in the quasistatic method was presented to solve the time-dependent multigroup diffusion equations for subcritical systems with external sources [2]. Parallelised Krylov methods were applied to the improved quasistatic approach in addition to the direct, implicit time difference, approach for solving space-time dependent multigroup neutron diffusion equations [3]. The nodal diffusion method was presented to solve space-time neutron kinetics using the finite element, primal and mixed hybrid nodal methods [4]. A one-step implicit method and a nodal modal method were studied for the solution of the time-dependent neutron diffusion equations which-based on a hexagonal spatial mesh [5–7]. An adiabatic kinetics model was developed for a boiling water reactor (BWR) core simulator AETNA [8]. Mathematical modeling of the space-time kinetics phenomena in advanced heavy water reactor, a 920 MW thermal, vertical pressure tube type thorium-based nuclear reactor, was presented using nodal modal method [9]. Class of Padé and cut-product approximations were applied to solve the two energy groups space-time nuclear reactor kinetics equations in two dimensions [10]. Adaptive Matrix Formation (AMF) method was presented and applied to homogeneous, symmetric heterogeneous, and nonsymmetric heterogeneous reactors in the cases of two and three dimensions [11]. The generalized Runge-Kutta method was developed for solving the multigroup, multidimensional, static, and transient neutron diffusion kinetics equations [12]. Computation accuracy and efficiency of a power series analytic method were presented for the time-space-dependent neutron diffusion equations with adiabatic heat up and doppler feedback [13]. The multigroup integro-differential equations of the neutron diffusion kinetics were presented and solved numerically in multislab geometry with the use of the progressive polynomial approximation [14].

The different kinds of Padé approximations were applied to the nonlinear point kinetics equations including temperature feedback via analytical inversion method [15, 16]. The straightforward recurrence relation of a power series was presented to solve the point kinetics equations in the presence of delayed neutrons with Newtonian feedback [17]. The stability of generalized Runge-Kutta method of order four was studied for the stiff system point kinetics equations with temperature feedback reactivity [18, 19]. The analytical exponential model was generalized to solve the point kinetics equations of beryllium and heavy water moderated reactors with step, ramp, and temperature feedback reactivities [20]. Power series solution (PWS) was applied for solving the point kinetics equations with lumped model temperature feedback [21]. Recently, new analytical solution, based on the roots of inhour equation, the eigenvalues of the coefficient matrix, was presented and applied for the point kinetics equations with the constant, ramp, and temperature feedback reactivities [22].

In this work, the two energy groups of the point kinetics equations and the average one group of delayed neutron are introduced. The generalization of the analytical exponential model is calculated using the eigenvalues and the eigenvectors of the coefficient matrix. The eigenvalues and the corresponding eigenvectors of the coefficient matrix are calculated. The results of the generalization of the analytical exponential model are compared with the results of the traditional methods.

2. Mathematical Model

The two energy groups neutron diffusion equations governing the dynamic groups diffusion neutron flux and average one group of the precursor concentration of delayed neutrons behavior are written as follows [23–25]:

()

where Φ₁(r, t) and Φ₂(r, t) are fast and thermal neutron flux, C(r, t) is average one group of the precursor concentration of delayed neutrons, D₁ and D₂ are fast and thermal diffusion coefficients,

and

are fast and thermal absorption cross-sections,

and

are fast and thermal fission cross-sections,

is the scattering cross-section from fast-to-thermal neutron, ν is the neutron fission, v₁ and v₂ are fast and thermal neutron speed, λ is decay constant of average one group of delayed neutrons, and β is the fraction of delayed neutrons.

The neutron flux and the precursor concentration of delayed neutrons can be written as separable functions of space and time as

()

where n₁(t) and n₂(t) are the fast and thermal neutron density, c(t) is the precursor concentration density of delayed neutrons and

is the fundamental function which can be determined from the following:

()

where B² is the material buckling.

Substituting (2.2) and (2.3) into (2.1) yields

()

Let us consider that

and

are fast and thermal generation time of neutrons,

and

are fast and thermal diffusion length,

and

are fast and thermal multiplication factor, ρ₁ = (k₁ − 1)/k₁ and ρ₂ = (k₂ − 1)/k₂ are fast and thermal reactivities,

, μ₁ = β/l₁ and μ₂ = β/l₂.

Equations (2.4) are rewritten in the following form:

()

Aboanber [26] presented two-energy group two-point kinetic model of reflected reactor. So, (2.5) can be called “two energy groups of the point kinetics equations”.

The initial values of this system, dn₁(0)/dt = dn₂(0)/dt = dc(0)/dt = 0, take the following form

()

and the material buckling takes the form:

()

3. Generalization of the Analytical Exponential Model

Let us rewrite (2.5) in matrix form as follows

()

where

()

Using the exponential integrator [27, 28], we can determine the general solution of (3.1) as follows:

()

where B is the integral constant.

This solution includes the exponential function of the matrix A which can be calculated using generalization of the analytical exponential model [20, 29] as

()

where B_k are the constants, ω_k are the eigenvalues of the matrix A and U_k are the corresponding eigenvectors of the matrix A.

Using the initial condition Ψ(0) = Ψ₀ to determine the constants

, (3.4) becomes as follows

()

where, V_k are the eigenvectors of matrix A^T which corresponding to eigenvalues ω_k and satisfies the normalization condition

. The eigenvectors U_k and V_k of the coefficient matrix A and A^T, respectively, are calculated analytically in the next subsections.

Equation (3.5) gives good results only for a constant matrix A. But for variable matrix A, the solution of the equation (3.1) can be takes the form

()

where, the values of the eigenvalues ω_k and the corresponding eigenvectors U_k and V_k are calculated at time t_m + (h/2), and h = t_m+1 − t_m is the time step interval [t_m, t_m+1].

Equations (3.5) and (3.6) represent the solutions of the two energy groups of point kinetics equation with average one group of delayed neutrons. These solutions represent a generalization of the analytical exponential model for step and variable coefficient matrix A, respectively.

3.1. Eigenvalues of the Matrix A

The eigenvalues of the matrix A are determined from the following algebraic equation:

()

The equation (3.7) is called “inhour equation.” This equation has a 3rd degree algebraic equation. To determine the roots of (3.7), we use the visual FORTRAN code, based on Laguerre’s numerical method, to calculate the roots of an algebraic equation with real coefficients.

3.2. Eigenvectors of the Matrix A

The eigenvectors of the matrix A are determined analytically as follows:

()

3.3. Eigenvectors of the Matrix A^T

The eigenvectors of the matrix A^T are determined analytically as follows:

()

where

is the normalization factor.

4. Results and Discussions

To check the accuracy of the results of the mathematical model of two energy groups of the homogeneous reactor kinetics equations, it is applied to the three-dimensional homogeneous reactor. This reactor is a bare homogeneous cube of side length 200 cm on each side with two neutron groups and one precursor group. The parameters of the three-dimensional homogeneous reactor are taken from [11] and shown in Table 1. The mathematical model of two energy groups of the point kinetics equations are solved by the generalization of the analytical exponential model (GAEM). Two different types of problems; step and ramp reactivities, are applied.

Table 1. Parameters of three-dimensional homogeneous reactor [11].

Parameter	Group 1	Group 2
Diffusion coefficient D (cm)	1.35	1.08
Absorption cross-section Σ_a (cm⁻¹)	0.001382	0.0054869
Neutron fission ν (neutron)	2.41	2.41
Fission cross-section Σ_f (cm⁻¹)	0.000242	0.00408
Scattering cross-section	0.0023	0.0
Velocity v (cm/s)	3.0 × 10⁷	2.2 × 10⁵

Decay constant λ (s⁻¹)	0.08
Fraction of delayed neutron β	0.0064
K_eff	0.8952858

4.1. Step Reactivity

The thermal neutron flux at the center point of the two energy groups of the homogeneous reactor kinetics equations with a positive step reactivity, , is calculated in Table 2. The results of the GAEM for the two energy groups of the point kinetics equations have an accuracy comparable with the results of the adaptive matrix formation (AMF) [11], 3DKIN [30] and the exact solution for the space-time nuclear reactor kinetics equations.

Table 2. Thermal neutron flux at the center point of three-dimensional homogeneous reactor with a positive step reactivity.

Time (s)	3DKIN	AMF	GAEM		Exact
Time (s)	h = 0.001	h = 0.0001	h = 0.001	h = 0.0001	Exact
0.0	0.816	0.816356	0.816356	0.816356	0.816
0.05	1.124	1.127264	1.127320	1.127300	1.127
0.10	1.406	1.407563	1.407587	1.407538	1.407
0.15	1.660	1.660798	1.660782	1.660695	1.660
0.20	1.890	1.890179	1.890112	1.889979	1.890
0.30	2.289	2.288396	2.288189	2.287949	2.288
0.40	2.622	2.621201	2.620796	2.620432	2.620

The fast and thermal neutron flux of the two energy groups of the point kinetics equations with a negative step reactivity, , is calculated in Table 3. This table substantiates the accuracy of the results of the GAEM compared with the results of the AMF [11].

Table 3. Neutron flux at the center point of three-dimensional homogeneous reactor with a negative step reactivity.

Time (s)	AMF		GAEM
Time (s)	Fast	Thermal	Fast	Thermal
0.0	2.228929	0.816356	2.228929	0.816356
0.05	1.645481	0.601048	1.645513	0.601060
0.10	1.409437	0.513969	1.409514	0.513998
0.15	1.313217	0.478479	1.313283	0.478504
0.20	1.273214	0.463731	1.273261	0.463748
0.30	1.247508	0.454268	1.247519	0.454272
0.40	1.239679	0.451400	1.239661	0.451394

Figure 1. shows the fast and thermal neutron flux at three values for positive step reactivities, and −3(0.0000369). And, the fast and thermal neutron flux at three types of negative step reactivities, and +3(0.0000369), are shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Fast and thermal neutron flux at a positive step reactivity.

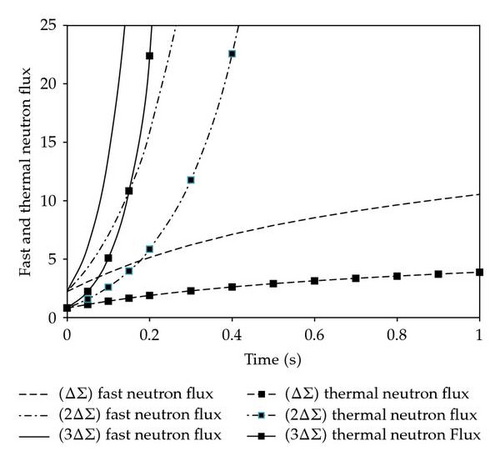
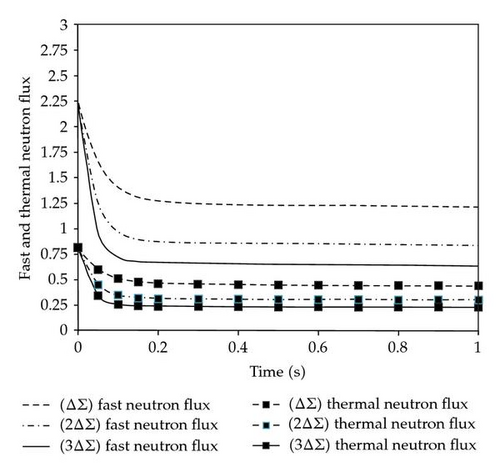
The calculation times, CPU times, of the GAEM to the AMF method are 0.43 s: 0.79 s at the same time step using personal desktop computer (processor: Core 2 Duo, 2.93 GHz). This means that the GAEM for two energy groups of the point kinetics equations is faster than the AMF for the space-time nuclear reactor kinetics equations.

4.2. Ramp Reactivity

To substantiate the accuracy and the efficiency of the generalization of the analytical exponential model for solving two energy groups of the point kinetics equations with linear ramp reactivity, it is applied to three dimensional homogeneous reactor. The fast and thermal neutron flux for a positive ramp reactivity, , are calculated in Table 4. This table is demonstrates the comparison between the results of the GAEM and AMF.

Table 4. Neutron flux at the center point of three dimensional homogeneous reactor with a positive ramp reactivity.

Time (s)	AMF		GAEM
Time (s)	Fast	Thermal	Fast	Thermal
0.0	2.228929	0.816356	2.228929	0.816356
0.05	2.276718	0.833995	2.276712	0.833993
0.10	2.399085	0.879151	2.399048	0.879137
0.15	2.580062	0.945931	2.579972	0.945898
0.20	2.816616	1.033217	2.816456	1.033158
0.30	3.484146	1.279522	3.483773	1.279385
0.40	4.529838	1.665354	4.529085	1.665078

The fast and thermal neutron flux of the two energy groups of the point kinetics equations with a negative ramp reactivity, , is calculated in Table 5.

Table 5. Neutron flux at the center point of three dimensional homogeneous reactor with a negative ramp reactivity.

Time (s)	AMF		GAEM
Time (s)	Fast	Thermal	Fast	Thermal
0.0	2.228929	0.816356	2.228929	0.816356
0.05	2.182204	0.799109	2.182170	0.799097
0.10	2.072954	0.758795	2.072892	0.758773
0.15	1.936615	0.708488	1.936528	0.708456
0.20	1.795565	0.656446	1.795460	0.656407
0.30	1.541171	0.562589	1.541033	0.562539
0.40	1.340555	0.488582	1.340396	0.488524

The fast and thermal neutron flux at different types of positive ramp reactivities, and −3(0.0000369 t), is shown in Figure 3. And also, the fast and thermal neutron flux at different types of negative ramp reactivities, and +3(0.0000369 t), are shown in Figure 4.

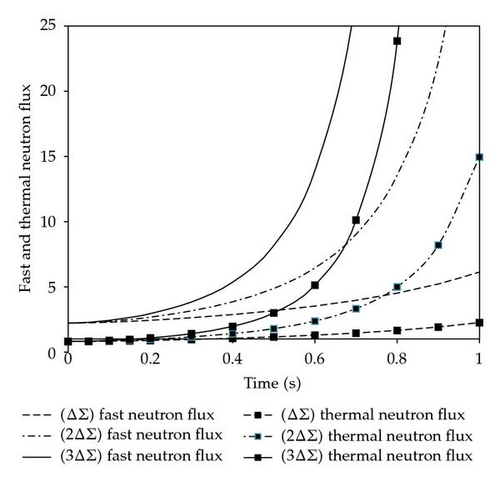
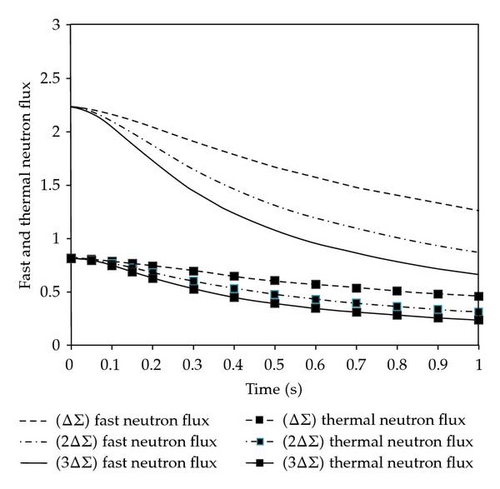
For ramp reactivity, The calculation times, CPU times, of the GAEM to the AMF method are 0.45 s: 0.81 s. This means, the GAEM is faster than the AMF.

5. Conclusions

Two energy groups of the point kinetics equations are represented a mathematical form for three dimensional homogeneous reactor kinetics equations and average one group of precursor delayed neutrons. The mathematical form was rewritten in the matrix form. Generalization of the analytical exponential model (GAEM) was developed to solve the new mathematical matrix form for three dimensional homogeneous reactor. This GAEM based on the eigenvalues and the corresponding eigenvectors of the coefficient matrix.

The results of GAEM were compared with the AMF, 3DKIN, and the exact solution for three dimensional homogeneous reactor. This comparison substantiated the accuracy of the results of the GAEM for different types of reactivities. In addition, the GAEM for the mathematical form, two energy groups of the point kinetics equations, is faster than any other traditional methods. So, this mathematical form may be one of the most important models for the neutron diffusion equations in the nuclear reactors.

References

1 Dahmani M., Baudron A. M., Lautard J. J., and Erradi L., A 3D nodal mixed dual method for nuclear reactor kinetics with improved quasistatic model and a semi-implicit scheme to solve the precursor equations, Annals of Nuclear Energy. (2001) 28, no. 8, 805–824, 2-s2.0-0035342171, https://doi.org/10.1016/S0306%2D4549(00)00089%2DX.
10.1016/S0306-4549(00)00089-X
CAS Web of Science® Google Scholar
2 Kobayashi K., A rigorous weight function for neutron kinetics equations of the quasi-static method for subcritical systems, Annals of Nuclear Energy. (2005) 32, no. 8, 763–776, 2-s2.0-16344362325, https://doi.org/10.1016/j.anucene.2005.01.011.
10.1016/j.anucene.2005.01.011
CAS Web of Science® Google Scholar
3 Gupta A., Modak R. S., Gupta H. P., Kumar V., and Bhatt K., Parallelised Krylov subspace method for reactor kinetics by IQS approach, Annals of Nuclear Energy. (2005) 32, no. 15, 1693–1703, 2-s2.0-28844448274, https://doi.org/10.1016/j.anucene.2005.05.003.
10.1016/j.anucene.2005.05.003
CAS Web of Science® Google Scholar
4 Grossman L. M. and Hennart J. P., Nodal diffusion methods for space-time neutron kinetics, Progress in Nuclear Energy. (2007) 49, no. 3, 181–216, 2-s2.0-34147139797, https://doi.org/10.1016/j.pnucene.2006.11.003.
10.1016/j.pnucene.2006.11.003
CAS Web of Science® Google Scholar
5 Ginestar D., Miro R., Verdu G., and Hennig D., A transient modal analysis of a BWR instability event, Journal of Nuclear Science and Technology. (2002) 39, no. 5, 554–563, 2-s2.0-0036577138.
10.1080/18811248.2002.9715234
CAS Web of Science® Google Scholar
6 Miró R., Ginestar D., Verdú G., and Hennig D., A nodal modal method for the neutron diffusion equation. Application to BWR instabilities analysis, Annals of Nuclear Energy. (2002) 29, no. 10, 1171–1194, 2-s2.0-0036643133, https://doi.org/10.1016/S0306%2D4549(01)00103%2D7.
10.1016/S0306-4549(01)00103-7
CAS Web of Science® Google Scholar
7 González-Pintor S., Ginestar D., and Verdú G., Time integration of the neutron diffusion equation on hexagonal geometries, Mathematical and Computer Modelling. (2010) 52, no. 7-8, 1203–1210, https://doi.org/10.1016/j.mcm.2010.03.020, 2718436.
10.1016/j.mcm.2010.03.020
Google Scholar
8 Tamitani M., Iwamoto T., and Moore B. R., Development of kinetics model for BWR core simulator AETNA, Journal of Nuclear Science and Technology. (2003) 40, no. 4, 201–212, 2-s2.0-0038538265.
10.1080/18811248.2003.9715350
CAS Web of Science® Google Scholar
9 Shimjith S. R., Tiwari A. P., Naskar M., and Bandyopadhyay B., Space-time kinetics modeling of Advanced Heavy Water Reactor for control studies, Annals of Nuclear Energy. (2010) 37, no. 3, 310–324, 2-s2.0-75849150246, https://doi.org/10.1016/j.anucene.2009.12.011.
10.1016/j.anucene.2009.12.011
CAS Web of Science® Google Scholar
10 Aboanber A. E. and Nahla A. A., Solution of two-dimensional space-time multigroup reactor kinetics equations by generalized Padé and cut-product approximations, Annals of Nuclear Energy. (2006) 33, no. 3, 209–222, 2-s2.0-32444445980, https://doi.org/10.1016/j.anucene.2005.11.003.
10.1016/j.anucene.2005.11.003
CAS Web of Science® Google Scholar
11 Aboanber A. E. and Nahla A. A., Adaptive matrix formation (AMF) method of space-time multigroup reactor kinetics equations in multidimensional model, Annals of Nuclear Energy. (2007) 34, no. 1-2, 103–119, 2-s2.0-33846913861, https://doi.org/10.1016/j.anucene.2006.07.012.
10.1016/j.anucene.2006.07.012
CAS Web of Science® Google Scholar
12 Aboanber A. E. and Hamada Y. M., Generalized Runge-Kutta method for two- and three-dimensional space-time diffusion equations with a variable time step, Annals of Nuclear Energy. (2008) 35, no. 6, 1024–1040, 2-s2.0-43449123063, https://doi.org/10.1016/j.anucene.2007.10.008.
10.1016/j.anucene.2007.10.008
CAS Web of Science® Google Scholar
13 Aboanber A. E. and Hamada Y. M., Computation accuracy and efficiency of a power series analytic method for two- and three- space-dependent transient problems, Progress in Nuclear Energy. (2009) 51, no. 3, 451–464, 2-s2.0-60449116418, https://doi.org/10.1016/j.pnucene.2008.10.003.
10.1016/j.pnucene.2008.10.003
CAS Web of Science® Google Scholar
14 Quintero-Leyva B., The multi-group integro-differential equations of the neutron diffusion kinetics. Solutions with the progressive polynomial approximation in multi-slab geometry, Annals of Nuclear Energy. (2010) 37, no. 5, 766–770, 2-s2.0-77950296202, https://doi.org/10.1016/j.anucene.2010.02.005.
10.1016/j.anucene.2010.02.005
CAS Web of Science® Google Scholar
15 Aboanber A. E. and Nahla A. A., Generalization of the analytical inversion method for the solution of the point kinetics equations, Journal of Physics. A. (2002) 35, no. 14, 3245–3263, https://doi.org/10.1088/0305%2D4470/35/14/307, 1914634.
10.1088/0305-4470/35/14/307
Google Scholar
16 Aboanber A. E. and Nahla A. A., Solution of the point kinetics equations in the presence of Newtonian temperature feedback by Padé approximations via the analytical inversion method, Journal of Physics. A. (2002) 35, no. 45, 9609–9627, https://doi.org/10.1088/0305%2D4470/35/45/309, 1946943.
10.1088/0305-4470/35/45/309
Google Scholar
17 Aboanber A. E. and Hamada Y. M., Power series solution (PWS) of nuclear reactor dynamics with newtonian temperature feedback, Annals of Nuclear Energy. (2003) 30, no. 10, 1111–1122, 2-s2.0-0037411137, https://doi.org/10.1016/S0306%2D4549(03)00033%2D1.
10.1016/S0306-4549(03)00033-1
CAS Web of Science® Google Scholar
18 Sanchez J., On the numerical solution of the point reactor kinetics equations by generalized Runge-Kutta methods, Nuclear Science and Engineering. (1989) 103, no. 1, 94–99, 2-s2.0-0024732173.
10.13182/NSE89-A23663
CAS Web of Science® Google Scholar
19 Aboanber A. E., Stability of generalized Runge-Kutta methods for stiff kinetics coupled differential equations, Journal of Physics. A. (2006) 39, no. 8, 1859–1876, https://doi.org/10.1088/0305%2D4470/39/8/006, 2209305.
10.1088/0305-4470/39/8/006
Google Scholar
20 Nahla A. A., Generalization of the analytical exponential model to solve the point kinetics equations of Be- and D2O-moderated reactors, Nuclear Engineering and Design. (2008) 238, no. 10, 2648–2653, 2-s2.0-49849094401, https://doi.org/10.1016/j.nucengdes.2008.04.002.
10.1016/j.nucengdes.2008.04.002
CAS Web of Science® Google Scholar
21 Sathiyasheela T., Power series solution method for solving point kinetics equations with lumped model temperature and feedback, Annals of Nuclear Energy. (2009) 36, no. 2, 246–250, 2-s2.0-58849163501, https://doi.org/10.1016/j.anucene.2008.11.005.
10.1016/j.anucene.2008.11.005
CAS Web of Science® Google Scholar
22 Nahla A. A., Analytical solution to solve the point reactor kinetics equations, Nuclear Engineering and Design. (2010) 240, no. 6, 1622–1629, 2-s2.0-77950936589, https://doi.org/10.1016/j.nucengdes.2010.03.003.
10.1016/j.nucengdes.2010.03.003
CAS Web of Science® Google Scholar
23 Hetrick D. L., Dynamics of Nuclear Reactors, 1993, American Nuclear Society, La Grange Park, Ill, USA.
Google Scholar
24 Glasstone S. and Sesonske A., Nuclear Reactor Engineering, 1994, Chapman & Hall.
10.1007/978-1-4615-7525-2_6
Google Scholar
25 Stacey W. M., Nuclear Reactor Physics, 2001, John Wiley & Sons, New York, NY, USA.
Google Scholar
26 Aboanber A. E., Spectral effects induced by the presence of a reflector for two-energy group two-point kinetic model of reflected reactors, Progress in Nuclear Energy. (2010) 52, no. 2, 197–205, 2-s2.0-70450224263, https://doi.org/10.1016/j.pnucene.2009.06.004.
10.1016/j.pnucene.2009.06.004
CAS Web of Science® Google Scholar
27 Blanes S. and Moan P. C., Fourth- and sixth-order commutator-free Magnus integrators for linear and non-linear dynamical systems, Applied Numerical Mathematics. (2006) 56, no. 12, 1519–1537, https://doi.org/10.1016/j.apnum.2005.11.004, 2257614.
10.1016/j.apnum.2005.11.004
Web of Science® Google Scholar
28 Hochbruck M. and Ostermann A., Exponential integrators, Acta Numerica. (2010) 19, 209–286, https://doi.org/10.1017/S0962492910000048, 2652783.
10.1017/S0962492910000048
Web of Science® Google Scholar
29 Quarteroni A., Sacco R., and Saleri F., Numerical Mathematics, 2000, 37, Springer, New York, NY, USA, Texts in Applied Mathematics, 1751750.
Web of Science® Google Scholar
30 Ferguson D. R. and Hansen K. F., Solution of the space-dependent reactor kinetics equations in the three dimension, Nuclear Science and Engineering. (1973) 51, 189–205.
10.13182/NSE73-A26594
CAS Web of Science® Google Scholar

Citing Literature

All articles

Generalization of the Analytical Exponential Model for Homogeneous Reactor Kinetics Equations

Abstract

1. Introduction

2. Mathematical Model