Volume 2012, Issue 1 246705

Research Article

Open Access

Decentralized Control of Uncertain Fuzzy Large-Scale System with Time Delay and Optimization

Hang Zhang,

Hang Zhang

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Xia Wang,

Xia Wang

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Yi-Jun Wang,

Corresponding Author

Yi-Jun Wang

[email protected]

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Zhao-Mei Sun,

Zhao-Mei Sun

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Hang Zhang,

Hang Zhang

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Xia Wang,

Xia Wang

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Yi-Jun Wang,

Corresponding Author

Yi-Jun Wang

[email protected]

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

Zhao-Mei Sun,

Zhao-Mei Sun

School of Information Science and Engineering, Central South University, Changsha 410075, China csu.edu.cn

Search for more papers by this author

First published: 26 March 2012

https://doi.org/10.1155/2012/246705

Citations: 1

Academic Editor: Huijun Gao

Share a link

Email
Wechat
Bluesky

Abstract

This paper studies the decentralized stabilization problem for an uncertain fuzzy large-scale system with time delays. The considered large-scale system is composed of several T-S fuzzy subsystems. The decentralized parallel distributed compensation (PDC) fuzzy control for each subsystem is designed to stabilize the whole system. Based on Lyapunov criterion, some sufficient conditions are proposed. Moreover, the positive definite matrices P_i and PDC gain K_ij can be solved by linear matrix inequality (LMI) toolbox of Matlab. Then, the optimization design method for decentralized control is also considered with respect to a quadratic performance index. Finally, numerical examples are given and compared with those of Zhang et al., 2004 to illustrate the effectiveness and less conservativeness of our method.

1. Introduction

Many real-life problems, such as power system, economic systems, societal system, and nuclear system are frequently of high dimension. Such systems are regarded as large-scale system. They consist of a number of subsystems which serve particular functions, share resources, and are governed by a set of interrelated goals and constrains [1]. Over the past decades, many methods have been to investigate the stability and stabilization of large-scale system [2–10].

Fuzzy systems of Takagi-Sugeno (T-S) models [11] have become an effective method to represent complex nonlinear dynamic system by fuzzy sets and fuzzy reasoning. The method of T-S model is feasible since, in many situations, human experts can provide linguistic descriptions of local systems in terms of IF-THEN rules [12–14]. Reference [15] proposed a control concept “parallel distributed compensation” (PDC) for fuzzy controller design of T-S fuzzy model. Under some conditions, PDC can stabilize the closed-loop fuzzy system asymptotically. Linear matrix inequalities (LMIs) methods to find the common positive matrix P_i always play a key role work in PDC design [16].

Now let us consider the control problem of large-scale system. Accordingly, suppose a large-scale system is composed of a number of subsystems with interconnection. Each subsystem is described by a T-S fuzzy model. That is, each subsystem dynamic is captured by a set of fuzzy implications that characterize local relations in the state space. Then, the global model of large-scale system can be achieved by smoothly connecting the local linear model in each fuzzy subspace together via the membership functions. Recently, the fuzzy decentralized control design methods and stability condition are addressed [17–24]. Wang and Luoh [17] have studied a fuzzy decentralized control design method for a fuzzy large-scale system on the assumption that all variables are available. Tseng and Chen [18] dealt with the model reference tracking control problem by using H_∞ decentralized fuzzy control, which relaxed the condition that the state variables are measurable. Wang and Zhang [19] considered the robust decentralized controller design method for nonlinear large-scale descriptor system. Hsiao et al. [20] proposed fuzzy decentralized control design methods for fuzzy large-scale system with time delays and gave the analysis of the closed-loop fuzzy large-scale system. Robust decentralized H_∞ output feedback controller was designed in [21]. Tong and Zhao [22] proposed a stabilization criterion of continuous-time interconnected fuzzy systems without uncertainties. Su and Liu [23] dealt with decentralized stabilization problem for a large-scale system in which the system is composed of several T-S fuzzy subsystems with nonlinear interconnections. Wang et al. [24] addressed robust H_∞ fuzzy controller design to overcome the parametric uncertainties of fuzzy large-scale systems without time delay and get H_∞ performance. Zhang et al. [25] proposed the stabilization problem of fuzzy large-scale system without parametric uncertainties.

However, the proposed decentralized control designs and the sufficient conditions of closed-loop system did not consider the parametric uncertainties or time delays, which is important in both theory and real-world application. In this paper, the stabilization problem of the uncertain fuzzy large-scale systems with time delays is considered. Based on decentralized control concept, we like to synthesize a PDC controller for each subsystem so that the whole system can be stabilized asymptotically. When applied to degenerated cases, (without uncertainties or time delay), the stabilization criteria are better than existing ones. Stability is one of the most important performance indecies, but it is not enough for control systems. Linear quadratic performance can reflect a lot of performance requirements, so a quadratic performance index is considered in this paper. Based on Lyapunov function stability theory, the optimization design method for decentralized control with respect to the quadratic performance index is transformed into solving linear inequality matrix by PDC controller.

This paper is organized as follows. In Section 2, the considered systems are stated and some preliminaries are presented.The problem of stabilization for fuzzy large-scale system with uncertainty is proposed in Section 3. Section 4 provides examples to illustrate the correctness of our theoretic results. Finally, a conclusion is given in Section 5.

2. System Description and Preliminaries

Consider a fuzzy large-scale system S, with uncertainties both in isolated subsystem and in their interconnection, which consists of J interconnected subsystems S_i. The ith fuzzy subsystem is described by the following equations:

(2.1)

where

(2.2)

for for all t ≥ 0, j = 1,2, …, r_i, k = 1,2, …, J, x_i(t) is the state vector, u_i(t) is the control input,

are known constant matrices with appropriate dimensions. τ_ki is the time delay. h_ij(t) is the normalized weigh in (2.6). F_ij(t) and

are time-varying matrices with appropriate dimensions satisfying

(2.3)

Each isolated subsystem S_i is represented by a T-S fuzzy model. The jth rule of this T-S fuzzy model is represented as follows.

Rule j. If z_1i(t) is M_j1i and … and z_pi(t) is M_jpi, then

(2.4)

where z_i(t) = [z_1i(t), z_2i(t), …, z_pi(t)] ^T, z_1i, …, z_pi(t) are premise variables, and M_jli (l = 1,2, …, p) are fuzzy sets. By “fuzzy blending,” the final output of the ith fuzzy subsystem is described as follows:

(2.5)

with

(2.6)

where M_jil(z_il(t)) is the grade of membership of z_il(t) in M_jil, and r_i is the number of fuzzy rules of subsystem S_i. We assumed that ω_ij(t) ≥ 0 for all t, j = 1,2, …, r_i. Therefore

(2.7)

Define a quadratic performance index

(2.8)

where Q_i and R_i are positive matrices.

The main propose of this paper is to synthesize a decentralized PDC fuzzy controller u_i(t) for each subsystem such that the closed-loop large-scale T-S fuzzy systems (2.1) is asymptotically stable and the optimization design method for decentralized control respect to the quadratic performance index.

Before starting the main results, we need the following lemmas.

Lemma 2.1 (see [26].)Let Q be any of n × n matrix; one will have for any constant k ≥ 0; and any positive matrix S > 0 that

(2.9)

for all x, y ∈ Rⁿ.

Lemma 2.2 (see [26].)Let D, E be any constant matrices and F^TF ≤ I, where a is a positive constant, all matrices with appropriate dimensions; one will have for any constant k > 0 such that

(2.10)

for all x, y ∈ Rⁿ.

Lemma 2.3 (see [27].)Let R_i be any positive matrix; one will have for any 0 ≤ h_ij(t) ≤ 1 such that

(2.11)

for all K_ij ∈ Rⁿ.

3. Stabilization and PDC Synthesis of Fuzzy Large-Scale System

In this section, the decentralized concept and PDC approach are applied to synthesize a local feedback controller for each local subsystem. Let the fuzzy controller be as the PDC form:

Rule j. If z_1i(t) is M_j1i and… and z_pi(t) is M_jpi, then

(3.1)

where i = 1,2, …, J, j = 1,2, …, r_i. The overall state feedback fuzzy control law is represented by:

(3.2)

Substituting (3.2) into (2.1), the closed-loop fuzzy subsystem becomes

(3.3)

Now, our work is to determine the local feedback gains K_ij such that the whole fuzzy large-scale system (3.3) is asymptotically stable.

Theorem 3.1. The fuzzy large-scale system (2.1) can be asymptotically stabilized by the decentralized PDC fuzzy control (3.2), if there exist matrices F_ij, positive definite matrices X_i to satisfy the following LMIs:

(3.4)

for i = 1,2, …, J, j = 1,2, …, r_i, n = 1,2, …, r_i, where

Proof. Let the Lyapunov functional be

(3.5)

where P_i > 0 is to be selected. It is obviously that there exist σ₁ and σ₂ such that

(3.6)

Taking the derivative of the V_i(t) along the trajectories of (3.3),

(3.7)

where

Using Lemma (2.2), we have

(3.8)

Using Lemma 2.1, we get

(3.9)

Noticing that the facts as follows:

(3.10)

Based on (3.7)–(3.10), we have

(3.11)

From Schur complement, we know

(3.12)

is equivalent to

(3.13)

where

, C_i = P_i[E_ij, C_1i, C_2i, …, C_Ji, D_1i, D_2i, …, D_Ji],

So we have while x_i(t) (i = 1,2, …, J) are not all zero vectors. Note that the matrix inequalities in (3.13) can be transformed into certain forms of linear matrix inequalities (LMIs). Therefore, multiplying both sides of matrix inequalities (3.13) by and applying the change of variables such that , , then (3.4) is obtained.

With the similar proof of Theorem 3.1, the stabilization criterion of large-scale system (2.1) without uncertainties is also discussed. The result is presented as follows.

Corollary 3.2. The fuzzy large-scale system (2.1) without uncertainties can be asymptotically stabilized by the decentralized PDC fuzzy control (3.2), if there exist matrices F_ij, positive definite matrices X_i to satisfy the following LMIs:

(3.14)

for i = 1,2, …, J, j = 1,2, …, r_i, n = 1,2, …, r_i, where

Proof. The proof is similar with that of Theorem 3.1; therefore details are omitted.

Remark 3.3. This corollary is similar with Theorem 1 in [10], so the theorem in this paper is more general.

Theorem 3.4. If there exist matrices F_ij, positive definite matrices X_i to satisfy the following LMIs:

(3.15)

the fuzzy large-scale system (2.1) can be asymptotically stabilized by the decentralized PDC fuzzy control (3.2), and the performance index (2.8) is satisfied the following inequality:

(3.16)

for i = 1,2, …, J, j = 1,2, …, r_i, n = 1,2, …, r_i, where

, L_iJ] ^T,

Proof. From the proof of Theorem 3.1, we know if

(3.17)

then

. Noticing that Q_i and R_i are positive matrices, if inequality

(3.18)

holds, we obtain

(3.19)

Using Lemma 2.3, we get

(3.20)

If (3.18) holds, we have

(3.21)

Therefore, multiply both sides of (3.18) by

, and let

. From Schur complement, the proof is completed.

4. Numerical Examples

In this section, some numerical simulations for uncertain fuzzy large-scale system will be given to illustrate the effectiveness of the proposed stabilization criteria and also compared with the existing results.

Example 4.1. Consider an uncertain FLSS time delays S composed of three fuzzy subsystems S_i, i = 1,2, 3 by the following equations:

(4.1)

in which

(4.2)

for i, k = 1,2, 3, j = 1,2.

(4.3)

Here, the T-S fuzzy models of the isolated subsystem are of the following:

Subsystem 1

Rule 1. If x₁₁(t) is M₁₁₁ then

(4.4)

Rule 2. If x₁₁(t) is M₂₁₁ then

(4.5)

and the membership functions for Rules 1 and 2 are, respectively, M₁₁₁(x₁₁(t)) = 1/(1 + exp⁡(−3x₁₁(t))), M₂₁₁(x₁₁(t)) = 1 − M₁₁₁(x₁₁(t)).

Subsystem 2

Rule 1. If x₁₂(t) is M₁₁₂ Then

(4.6)

Rule 2. If x₁₂(t) is M₂₁₂ then

(4.7)

and the membership functions for Rules 1 and 2 are, respectively,

, M₂₁₂(x₁₂(t)) = 1 − M₁₁₂(x₁₂(t)).

Subsystem 3

Rule 1. If x₁₃(t) is M₁₁₃ then

(4.8)

Rule 2. If x₁₃(t) is M₂₁₃ then

(4.9)

and the membership functions for Rules 1 and 2 are, respectively, M₁₁₃(x₁₃(t)) = 1/(1 + exp⁡(−1.5x₁₃(t))), M₂₁₃(x₁₃(t)) = 1 − M₁₁₃(x₁₃(t)).

It is noted that the above large-scale system without control (u_i(t) = 0) has unstable responses with initial conditions x₁(t) = [−3,3] ^T, x₂(t) = [−2,2] ^T, x₃(t) = [1, −1] ^T as shown in Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The state response with u_i(t) = 0.

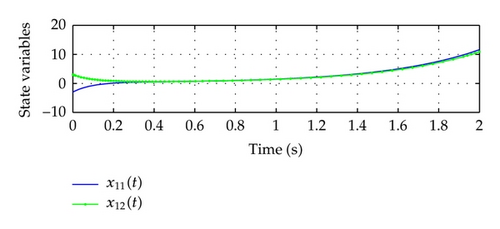
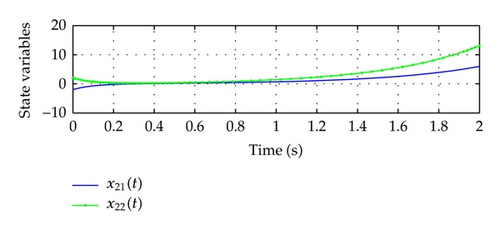
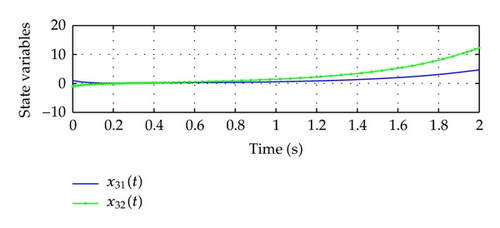
In order to stabilize the large-scale fuzzy system, three decentralized PDC fuzzy controllers are designed in the following.

Fuzzy Controller C1

Rule 1. If x₁₁(t) is M₁₁₁ then

(4.10)

Rule 2. If x₁₁(t) is M₂₁₁ then

(4.11)

Fuzzy Controller C2

Rule 1. If x₁₂(t) is M₁₁₂ then

(4.12)

Rule 2. If x₁₂(t) is M₂₁₂ then

(4.13)

Fuzzy Controller C3

Rule 1. If x₁₃(t) is M₁₁₃ then

(4.14)

Rule 2. If x₁₃(t) is M₂₁₃ Then

(4.15)

By using the approaches of Theorem 3.1, we obtain the matrices K_ij for subsystems S₁, S₂, and S₃:

(4.16)

The complete simulation results with initial conditions x₁(t) = [−3,3] ^T, x₂(t) = [−2,2] ^T, x₃(t) = [1, −1] ^T are shown in Figure 2. It is obvious that they are stabilized asymptotically.

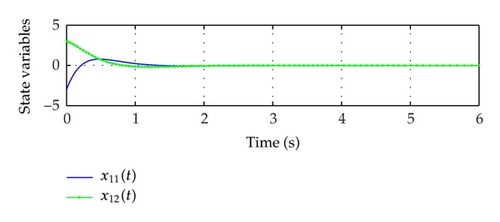
Example 4.2. Consider the fuzzy large-scale system S composed of two subsystems S_i as follows [25]:

(4.17)

where x₁(t) = [x₁₁(t), x₁₂(t)] ^T, x₂(t) = [x₂₁(t), x₂₂(t)] ^T

(4.18)

and the membership functions are, respectively,

, M₂₁₁(x₁₁(t)) = 1 − M₁₁₁(x₁₁(t)), M₁₁₂(x₂₁(t)) = 1/(1 + exp⁡(−x₂₁(t))), M₂₁₂(x₂₁(t)) = 1 − M₁₁₂(x₂₁(t)).

In order to stabilize the large-sale fuzzy system, three decentralized PDC fuzzy controllers are designed in the following.

Fuzzy Controller C1

Rule 1. If x₁₁(t) is M₁₁₁ then

(4.19)

Rule 2. If x₁₁(t) is M₂₁₁ then

(4.20)

Fuzzy Controller C2

Rule 1. If x₂₁(t) is M₁₁₂ then

(4.21)

Rule 2. If x₂₁(t) is M₂₁₂ then

(4.22)

We let

, R₁ = 1, R₂ = 2. By using the approaches of Theorem 3.4, we obtain

(4.23)

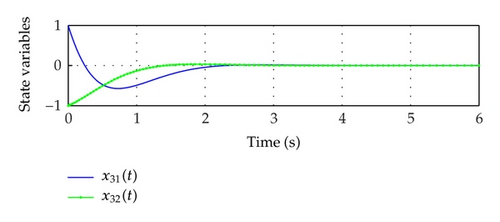
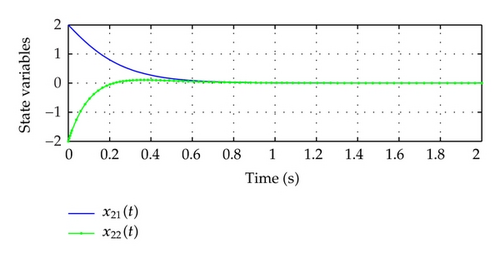
The control gain K_ij for subsystem S₁, S₂ is compared with [24] in Table 1. The complete simulation results with initial conditions x₁(t) = [1, −1] ^T, x₂(t) = [2, −2] ^T are shown in Figure 3.

Table 1. Comparison of fuzzy controller, for example, with Zhang et al. [25].

Index	K₁₁	K₁₂	K₂₁	K₂₂	J^*	∥K∥₂
Zhang et al. [25]	[10.7602 4.8931]	[7.1424 1.0899]	[2.2702 0.1348]	[1.9527 0.8715]	21.0606	14.2011
This paper	[9.0414 1.0000]	[2.0000 1.8284]	[1.1604 0.0740]	[0.3515 2.2722]	12.2288	9.8351

Remark 4.3. From Figure 3, we can see that the system can be stabilized through appropriate decentralized control. Obviously, in Table 1, we can see the method of this paper has smaller gain matrices and performance index, so it has better control effectiveness.

5. Conclusions

In this paper we explore the stabilization problems for uncertain fuzzy large-scale system with time delays. The decentralized PDC fuzzy controller has been designed under some conditions such that the whole closed-loop large-scale fuzzy system is asymptotically stable. Then, the optimization design method for decentralized control is also considered with respect to a quadratic performance index. Finally, numerical examples are provided to demonstrate the correctness and less conservativeness of the theoretical results. However, there are still some other problems to be addressed, such that time-varying delays and delay-dependent stability and stabilization of fuzzy large-scale system and the results developed in the paper can be extended to the case that the underlying systems are invovled with any switching dynamics.

Acknowledgment

This work is supported by the National Natural Science Foundation of China (60774045, 61075065).

References

1 Michel A. N. and Miller R. K., Qualitative Analysis of Large Scale Dynamical Systems, 1977, Academic Press, New York, NY, USA, 0444204, ZBL0494.93002.
Google Scholar
2 Chen B.-S. and Wang W.-J., Robust stabilization of nonlinearly perturbed large-scale systems by decentralized observer-controller compensators, Automatica. (1990) 26, no. 6, 1035–1041, https://doi.org/10.1016/0005%2D1098(90)90087%2DX.
10.1016/0005-1098(90)90087-X
Web of Science® Google Scholar
3 Cheng C.-F., Design of robust observation schemes for uncertain large scale systems, IEE Proceedings. (1997) 144, no. 5, 369–373.
Google Scholar
4 Gong Z., Decentralized robust control of uncertain interconnected systems with prescribed degree of exponential convergence, IEEE Transactions on Automatic Control. (1995) 40, no. 4, 704–707, 1324865, https://doi.org/10.1109/9.376105, ZBL0825.93660.
10.1109/9.376105
Web of Science® Google Scholar
5 Guan Z. H., Liu Y. Q., and Wen X. C., Decentralized stabilization of singular and time-delay large-scale control systems with impulsive solutions, IEEE Transactions on Automatic Control. (1995) 40, no. 8, 1437–1441, 1343810, https://doi.org/10.1109/9.402236, ZBL0836.93052.
10.1109/9.402236
Web of Science® Google Scholar
6 Jiang Z.-P., Repperger D. W., and Hill D. J., Decentralized nonlinear output-feedback stabilization with disturbance attenuation, IEEE Transactions on Automatic Control. (2001) 46, no. 10, 1623–1629, 1858067, https://doi.org/10.1109/9.956061, ZBL1049.93077.
10.1109/9.956061
Web of Science® Google Scholar
7 Labibi B., Lohmann B., Sedigh A. K., and Maralani P. J., Sufficient condition for stability of decentralised control, Electronics Letters. (2000) 36, no. 6, 588–590, https://doi.org/10.1049/el:20000392.
10.1049/el:20000392
Web of Science® Google Scholar
8 Liu P.-L. and Su T.-J., Stability for single and large-scale uncertain systems with time-varying delays, IEE Proceedings. (1999) 146, no. 6, 591–597, https://doi.org/10.1049/ip%2Dcta:19990681.
10.1049/ip-cta:19990681
Google Scholar
9 Tsay J.-T., Liu P.-L., and Su T.-J., Robust stability for perturbed large-scale time-delay systems, IEE Proceedings. (1996) 143, no. 3, 233–236.
Google Scholar
10 Zhang H. B. and Yu J. B., LMI-based stability analysis of fuzzy large-scale systems with time delays, Chaos, Solitons and Fractals. (2005) 25, no. 5, 1193–1207, 2144663, https://doi.org/10.1016/j.chaos.2004.11.065, ZBL1142.93376.
10.1016/j.chaos.2004.11.065
Web of Science® Google Scholar
11 Takagi T. and Sugeno M., Fuzzy identification of systems and its applications to modeling and control, IEEE Transactions on Systems, Man and Cybernetics. (1985) 15, no. 1, 116–132.
10.1109/TSMC.1985.6313399
Web of Science® Google Scholar
12 Tanaka K. and Wang H., Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach, 2001, John Wiley and Sons, New York, NY, USA.
10.1002/0471224596
Google Scholar
13 Zadeh L. A., Outline of new approach to the analysis of complex systems and decision processes, IEEE Transactions on Systems, Man, and Cybernetics. (1973) 3, no. 1, 28–44, 0309582, ZBL0273.93002.
10.1109/TSMC.1973.5408575
Web of Science® Google Scholar
14 Emami M. R., Türksen I. B., and Goldenberg A. A., Development of a systematic methodology of fuzzy logic modeling, IEEE Transactions on Fuzzy Systems. (1998) 6, no. 3, 346–361, https://doi.org/10.1109/91.705501.
10.1109/91.705501
Web of Science® Google Scholar
15 Tanaka K. and Sugeno M., Stability analysis and design of fuzzy control systems, Fuzzy Sets and Systems. (1992) 45, no. 2, 135–156, https://doi.org/10.1016/0165%2D0114(92)90113%2DI, 1149415, ZBL0758.93042.
10.1016/0165-0114(92)90113-I
Web of Science® Google Scholar
16 Wang H. O., Tanaka K., and Griffin M. F., An approach to fuzzy control of nonlinear systems: stability and design issues, IEEE Transactions on Fuzzy Systems. (1996) 4, no. 1, 14–23, https://doi.org/10.1109/91.481841.
10.1109/91.481841
Web of Science® Google Scholar
17 Wang W.-J. and [email protected], Luoh L., Stability and stabilization of fuzzy large-scale systems, IEEE Transactions on Fuzzy Systems. (2004) 12, no. 3, 309–315, https://doi.org/10.1109/TFUZZ.2004.825975.
10.1109/TFUZZ.2004.825975
Web of Science® Google Scholar
18 Tseng C.-S. and Chen B.-S., H_∞ decentralized fuzzy model reference tracking control design for nonlinear interconnected systems, IEEE Transactions on Fuzzy Systems. (2001) 9, no. 6, 795–809, https://doi.org/10.1109/91.971729.
10.1109/91.971729
Web of Science® Google Scholar
19 Wang Y. and Zhang Q.-L., Robust fuzzy decentralized control for nonlinear interconnected descriptor, 24, Proceedings of the IEEE Conference on Fuzzy Systems, 2001, 1392–1395.
Google Scholar
20 Hsiao F.-H., [email protected], Hwang J.-D., Chen C.-W., and Tsai Z.-R., Robust stabilization of nonlinear multiple time-delay large-scale systems via decentralized fuzzy control, IEEE Transactions on Fuzzy Systems. (2005) 13, no. 1, 152–163, https://doi.org/10.1109/TFUZZ.2004.836067.
10.1109/TFUZZ.2004.836067
Web of Science® Google Scholar
21 Xie Y., [email protected], Huang C., [email protected], Gui W., [email protected], Jiang Z., and [email protected], Yang C., [email protected], Decentralized robust H_∞ output feedback control for value bounded uncertain large-scale interconnected systems, Proceedings of the 26th Chinese Control Conference (CCC ′07), 2007, 583–589, https://doi.org/10.1109/CHICC.2006.4346884.
10.1109/CHICC.2006.4346884
Google Scholar
22 Tong S. C. and Zhao F. F., Decentralized fuzzy control and a new stabilization criterion for interconnected fuzzy systems, Control and Decision. (2009) 24, no. 8, 1235–1238, 2562890.
Google Scholar
23 Su K. and [email protected], Liu X., [email protected], Decentralized controllers for uncertain FLSS, 1, Proceedings of the IEEE International Conference on Automation and Logistics (ICAL ′08), 2008, 492–497, https://doi.org/10.1109/ICAL.2008.4636201.
10.1109/ICAL.2008.4636201
Google Scholar
24 Wang W.-J., [email protected], Lin W.-W., and Yang S.-H., Stabilization for large-scale fuzzy systems with decentralized fuzzy control, 2, Proceedings of the IEEE International Conference on Systems, Man and Cybernetics, 2007, 1716–1720, https://doi.org/10.1109/ICSMC.2006.384967.
10.1109/ICSMC.2006.384967
Google Scholar
25 Zhang Y.-G., Jing X., and Jian X., Decentralized stabilization of continuous-time fuzzy large-scale systems via LMI method, Systems Engineering and Electronics. (2004) 26, no. 6, 773–776.
Google Scholar
26 Yi Z. and Heng P. A., Stability of fuzzy control systems with bounded uncertain delays, IEEE Transactions on Fuzzy Systems. (2002) 10, no. 1, 92–96, https://doi.org/10.1109/91.983283.
10.1109/91.983283
Web of Science® Google Scholar
27 Guan X.-P. and [email protected], Chen C.-L., [email protected], Delay-dependent guaranteed cost control for T-S fuzzy systems with time delays, IEEE Transactions on Fuzzy Systems. (2004) 12, no. 2, 236–249, https://doi.org/10.1109/TFUZZ.2004.825085.
10.1109/TFUZZ.2004.825085
Web of Science® Google Scholar

Citing Literature

All articles

Decentralized Control of Uncertain Fuzzy Large-Scale System with Time Delay and Optimization

Abstract

1. Introduction

2. System Description and Preliminaries

3. Stabilization and PDC Synthesis of Fuzzy Large-Scale System

4. Numerical Examples

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Decentralized Control of Uncertain Fuzzy Large-Scale System with Time Delay and Optimization

Abstract

1. Introduction

2. System Description and Preliminaries

3. Stabilization and PDC Synthesis of Fuzzy Large-Scale System

4. Numerical Examples

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information