Journal of Applied Mathematics
Volume 2012, Issue 1 245051
Research Article
Open Access

Finite Element Preconditioning on Spectral Element Discretizations for Coupled Elliptic Equations

JongKyum Kwon, 

JongKyum Kwon

Department of Mathematics, Kyungpook National University, Daegu 702-701, Republic of Korea knu.ac.kr

Search for more papers by this author
Soorok Ryu, 

Soorok Ryu

Department of Mathematics, Kyungpook National University, Daegu 702-701, Republic of Korea knu.ac.kr

Search for more papers by this author
Philsu Kim, 

Philsu Kim

Department of Mathematics, Kyungpook National University, Daegu 702-701, Republic of Korea knu.ac.kr

Search for more papers by this author
Sang Dong Kim, 

Corresponding Author

Sang Dong Kim

Department of Mathematics, Kyungpook National University, Daegu 702-701, Republic of Korea knu.ac.kr

Search for more papers by this author
First published: 12 February 2012
https://doi.org/10.1155/2012/245051
Citations: 2
Academic Editor: Massimiliano Ferronato

Abstract

The uniform bounds on eigenvalues of are shown both analytically and numerically by the 𝒫1 finite element preconditioner for the Legendre spectral element system which is arisen from a coupled elliptic system occurred by an optimal control problem. The finite element preconditioner is corresponding to a leading part of the coupled elliptic system.

1. Introduction

Optimal control problems constrained by partial differential equations can be reduced to a system of coupled partial differential equations by Lagrange multiplier method ([1]). In particular, the needs for accurate and efficient numerical methods for these problems have been important subjects. Many works are reported for solving coupled partial differential equations by finite element/difference methods; or finite element least-squares methods ([2–5], etc.). But, there are a few literature (for examples, [6, 7]) on coupled partial differential equations using the spectral element methods (SEM) despite of its popularity and accuracy (see, e.g., [8]).

One of the goals in this paper is to investigate a finite element preconditioner for the SEM discretizations. The induced nonsymmetric linear systems by the SEM discretizations from such coupled elliptic partial differential equations have the condition numbers which are getting larger incredibly not only as the number of elements and degrees of polynomials increases but also as the penalty parameter δ decreases (see [5] and Section 4). Hence, an efficient preconditioner is necessary to improve the convergence of a numerical method whose number of iterations depends on the distributions of eigenvalues (see [9–12]). Particularly, the lower-order finite element/difference preconditioning methods for spectral collocation/element methods have been reported ([9, 10, 13–17], etc.).

The target-coupled elliptic type equations are as follows:
()
which is the result of Lagrange multiplier rule applied to a L2 optimal control problem subject to an elliptic equation (see [1]). Applying the 𝒫1 finite element preconditioner to our coupled elliptic system discretized by SEM using LGL (Legendre-Gauss-Lobatto) nodes, we show that the preconditioned linear systems have uniformly bounded eigenvalues with respect to elements and degrees.

The field of values arguments will be used instead of analyzing eigenvalues directly because the matrix representation of the target operator, even with zero convection term, is not symmetric. We will show that the real parts of eigenvalues are positive, uniformly bounded away from zero, and the absolute values of eigenvalues are uniformly bounded whose bounds are only dependent on the penalty parameter δ in (1.1) and the constant vector b in (1.1). Because of this result, one may apply a lower-order finite element preconditioner to a real optimal control problem subject to Stokes equations which requires an elliptic type solver.

This paper is organized as follows: in Section 2, we introduce some preliminaries and notations. The norm equivalences of interpolation operators are reviewed to show the norm equivalence of an interpolation operator using vector basis. The preconditioning results are presented theoretically and numerically in Section 3 and Section 4, respectively. Finally, we add the concluding remarks in Section 5.

2. Preliminaries

2.1. Coupled Elliptic System

Because we are going to deal with a coupled elliptic system, the vector Laplacian, gradient and divergence operators for a vector function , where T denotes the transpose, are defined by
()
With the usual L2 inner product 〈·, ·〉 and its norm ∥·∥, for vector functions and , define
()
and, for matrix functions U and V, define
()

We use the standard Sobolev spaces like H1(Ω) and on a given domain Ω with the usual Sobolev seminorm |·|1 and norm ∥·∥1. The main content of this paper is to provide an efficient low-order preconditioner for the system (1.1).

Multiplying the second equation by 1/δ, the system (1.1) can be expressed as
()
where
()
with the zero boundary condition . Let ℬ be another decoupled uniformly elliptic operator such that
()
with the zero boundary condition.

2.2. LGL Nodes, Weights, and Function Spaces

Let and be the reference LGL nodes and its corresponding LGL weights in I = [−1,1], respectively, arranged by −1 = :η0 < η1 < ⋯<ηN−1 < ηN∶ = 1. We use as the set of knots in the interval I such that −1 = :t0 < t1 < ⋯<tE−1 < tE∶ = 1. Here E denotes the number of subintervals of I. Denote N by the degree of a polynomial on each subinterval Ij∶ = [tj−1, tj] and by the set of kth-LGL nodes ξj,k in each subinterval Ij (j = 1, …, E) arranged by
()
where
()
and the corresponding LGL weights are given by
()
Let 𝒫k be the space of all polynomials defined on I whose degrees are less than or equal to k. The Lagrange basis for 𝒫N on I is given by satisfying
()
where δij denotes the Kronecker delta function.
We define as the subspace of continuous functions whose basis is piecewise continuous Lagrange polynomials of degree N on Ij with respect to 𝒢 and define as the space of all piecewise Lagrange linear functions with respect to 𝒢. Note that these basis functions have a proper support. See [9, 18] for detail. Let and . With the notation 𝒱 × 𝒱∶ = {[u,v]T   |   u, v ∈ 𝒱}, define and as subspaces of and , respectively. The basis functions for and are given respectively by
()
where p = 1,2, …, 2𝔑. For two dimensional (2D) case, let and be tensor product function spaces of one-dimensional function spaces and let and be subspaces of and , respectively. Now let us order the interior LGL points in Ω by horizontal lines as , where for μ, ν = 1,2, …, 𝔑. Accordingly, the basis functions for and are also arranged as the same way. Then, with the notations and , the basis functions of and are given, respectively, by
()
where .

2.3. Interpolation Operators

We denote C(Ω) as the set of continuous functions in Ω∶ = I × I. Let be the usual reference interpolation operator such that for u ∈ C(Ω) (see, e.g., [17]). The global interpolation operator is given by , where . Hence, it follows that for u ∈ C(Ω). With this interpolation operator , let us define the vector interpolation operator such that, for ,
()
Let and , where and i, j = 0, …, N, be the basis of [[𝒫N]] and [[𝒱N]], respectively. Let us denote and by the mass matrices such that
()
and denote and by the stiffness matrices such that
()
where .
According to Theorems 5.4 and 5.5 in [17], there are two absolute positive constants c0 and c1 such that for any ,
()
and for all u ∈ [[𝒱N]],
()
The extension of (2.17) to the interpolation operator leads to
()
for all , where the constants c0 and c1 are positive constants independent of E and N (see [18]).

Theorem 2.1. For all , there are positive constants c0 and c1 independent of E and N such that

()

Proof. By the definitions of the interpolation operator and the norms, we have

()
which completes the proof because of (2.18).

3. Analysis on 𝒫1 Finite Element Preconditioner

The bilinear forms corresponding to (2.4) and (2.6) are given by
()
()
where , and are the same matrices in (2.4) and . Note that the bilinear form β(·, ·) in (3.2) is symmetric but the bilinear form α(·, ·) in (3.1) is not symmetric. The following norm equivalence guarantees the existence and uniqueness of the solution in for the variational problem (3.1).

Proposition 3.1. For a real valued vector function , we have

()

Proof. Since b is a constant vector, , and is a real valued vector function, we have

()
Hence, (3.3) is proved because 0 < δ ≤ 1.

Lemma 3.2. If is a complex valued function in , then we have the following estimates:

()
where .

Proof. Let us decompose u and v in as u(x, y) = p(x, y) + iq(x, y) and v(x, y) = r(x, y) + is(x, y), where p, q, r, and s are real functions and i2 = −1. Then we have

()
()
()
Hence, one may see that the real part of is and the pure imaginary part is the sum of (3.6), (3.7), and (3.8). By Cauchy-Schwarz inequality, ϵ-inequality, and the range of 0 < δ ≤ 1, we have
()
Hence (3.5) is proved.

Let and be the spectrum (or set of eigenvalues) and field of values of the square matrix , respectively. Let and be the two dimensional stiffness matrices on the spaces and induced by (3.1) and (3.2), respectively. Then, we have the following.

Lemma 3.3. For , one has

()
where
()

Proof. Since is symmetric positive definite, there exists a unique positive definite square root of . So, we have

()
for . Now let be a short-hand notation for . Therefore, from the relation of spectrum and field of values (see [19] or [11]), it follows that
()
which completes the proof.

The following theorem shows the uniform bounds of eigenvalues which is independent of both N and E for our preconditioned system
()

Theorem 3.4. Let be the set of eigenvalues of

()
then, there are constants c0, C0, and Λδ independent of E and N, such that
()
where Λδ = C(1 + ∥b∥ + 1/δ).

Proof. Let be represented as . Then, its piecewise polynomial interpolation can be written as

()
Let . From the definitions of the bilinear forms, we have
()
This implies that
()
By Theorem 2.1 and Lemma 3.2, the real part of wλ satisfies
()
where the notation a ~ b means the equivalence of two quantities a and b which does not depend on E and N. Again, from Theorem 2.1 and Lemma 3.2, the absolute value of wλ satisfies
()
Therefore, from Lemma 3.3, the real parts and the absolute values of eigenvalues of satisfy (3.16).

Remark 3.5. Let the one dimensional (1D) bilinear forms for be

()
()
and denote and by the 1D stiffness matrices on the spaces and corresponding to the bilinear forms (3.22) and (3.23), respectively. Then one can easily get the same results as Theorem 3.4 for 1D case. Since the proof is similar to 2D case, we omit the statements.

Now, for actual numerical computations, we need 2D stiffness and mass matrices expressed as the tensor products of 1D matrices (see [20] for details). For this, let us denote 1D spectral element matrices as
()
and 1D finite element matrices
()
where and are the Lagrange basis of the spaces and , respectively. For actual computations for , , and , the inner product 〈·, ·〉 on the space will be computed using LGL quadrature rule at LGL nodes. Without any confusion, such approximate matrices can be denoted by same notations in the next section. We note that the approximate matrices , , and and the exact matrices , , and are equivalent, respectively, because of the equivalence of LGL quadrature on the polynomial space we used. For example, the mass matrix can be computed using the LGL weights {ρj,k} only.

4. Numerical Tests of Preconditioning

4.1. Matrix Representation

In this section we discuss effects of the proposed finite element preconditioning for the spectral element discretizations to the coupled elliptic system (1.1). For this purpose, first we set up one dimensional matrices and corresponding to (3.22) and (3.23) using the matrices in (3.24). One may have
()
Let be a constant vector in (1.1), then the 2D matrices and can be expressed as
()
where
()

4.2. Numerical Analysis on Eigenvalues

The linear system and the preconditioned linear system will be compared in the sense of the distribution of eigenvalues. As proved in Section 3, it is shown that the behaviors of spectra of are independent of the number of elements and degrees of polynomials.

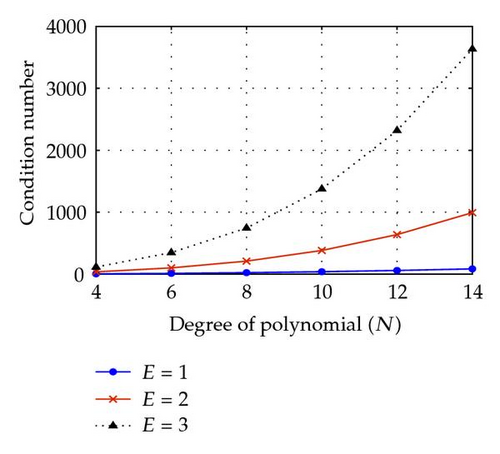
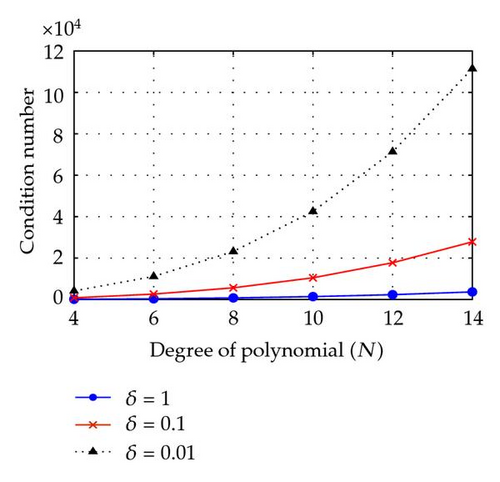
One may also see the condition numbers of these discretized systems by varying the penalty parameter δ. The condition numbers of are presented in Figure 1 for fixed δ = 1 (left) and fixed E = 3 (right) as increasing the degrees N of polynomials. It shows that such condition numbers depend on N, E, and δ. In particular, the smaller δ is, the larger condition number it yields.

Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
The condition numbers of the matrix when b = [1,1]T.
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
The condition numbers of the matrix when b = [1,1]T.

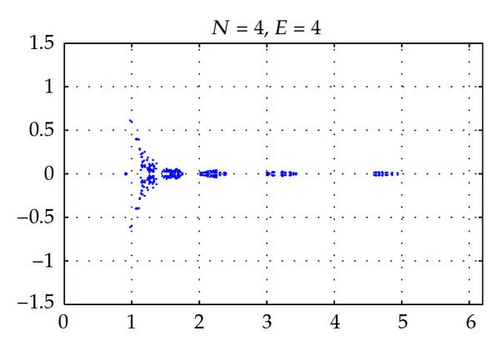
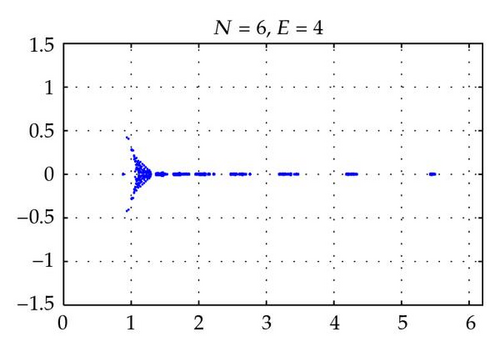
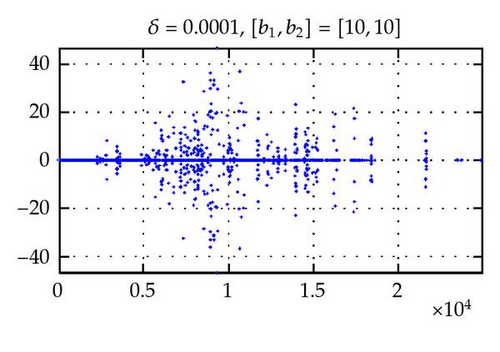
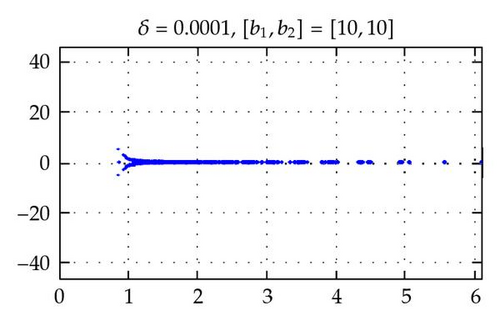
Figures 2 and 4 show the spectra of the resulting preconditioned operator for the polynomials of degrees N = 4,6, 8,10 and E = 4 when δ = 1 and δ = 10−4, respectively. Also, Figures 3 and 5 show the spectra of for E = 4,6, 8,10 and N = 4 for δ = 1 and δ = 10−4, respectively. The same axis scales are presented for the same δ when b = [1,1]T. As proven in Theorem 3.4, the eigenvalues of are independent of N and E, but they depend still on the penalty parameter δ.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 2 (d)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 1, b = [1,1]T.
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
The eigenvalues of for N = 4,6, 8,10 and E = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 10−4, b = [1,1]T.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
The eigenvalues of for E = 4,6, 8,10 and N = 4 when δ = 10−4, b = [1,1]T.

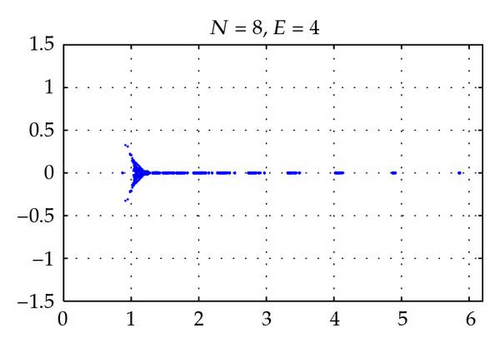
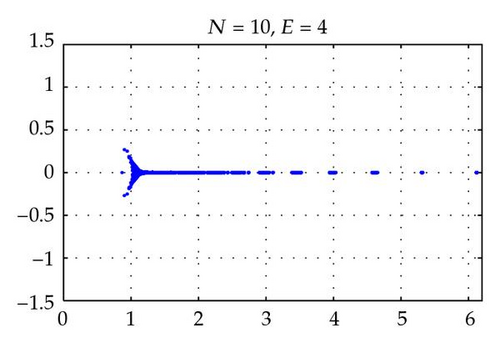
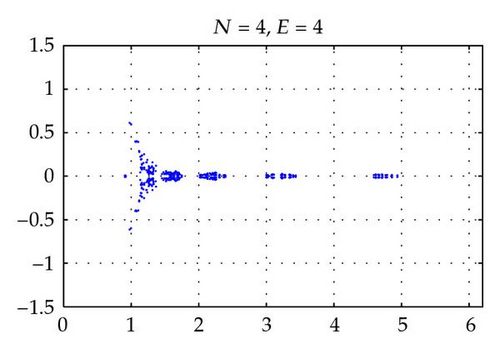
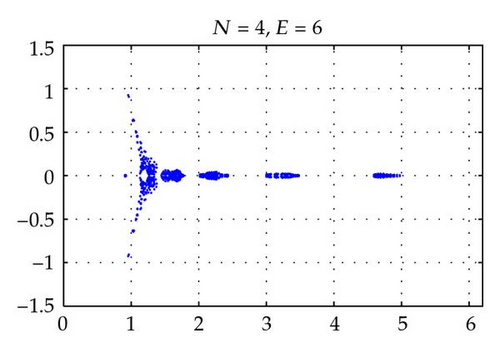
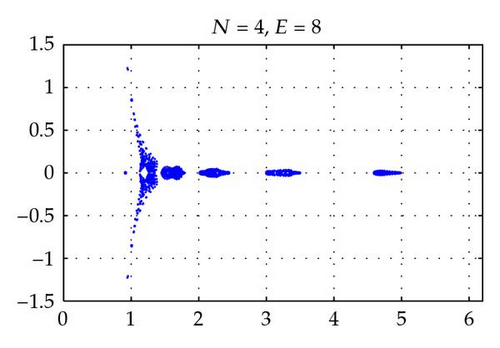
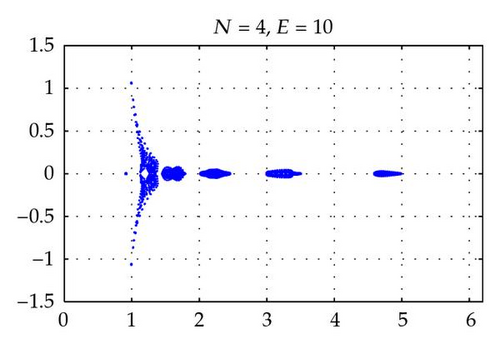
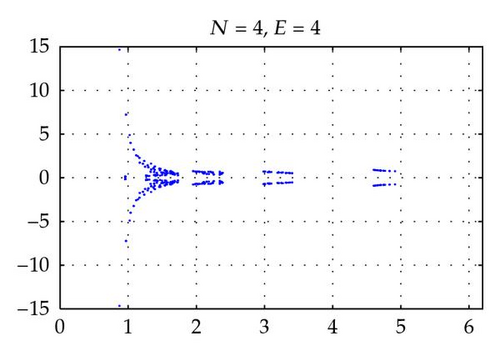
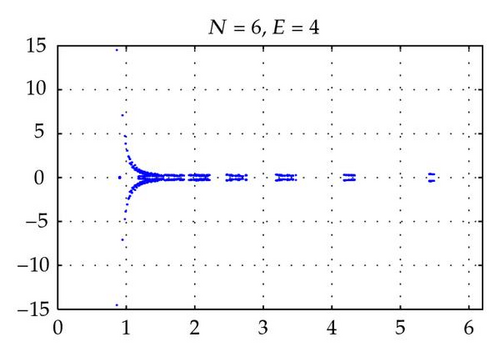
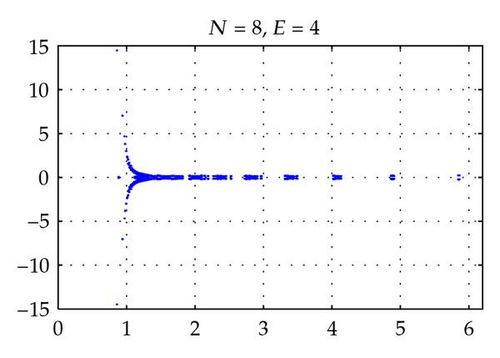
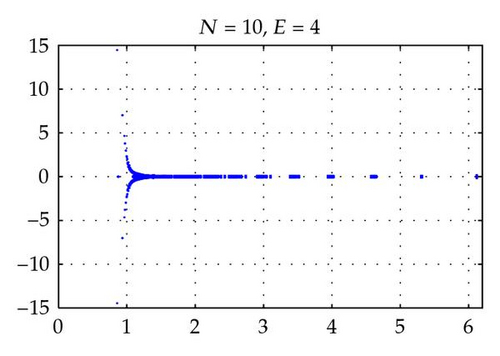
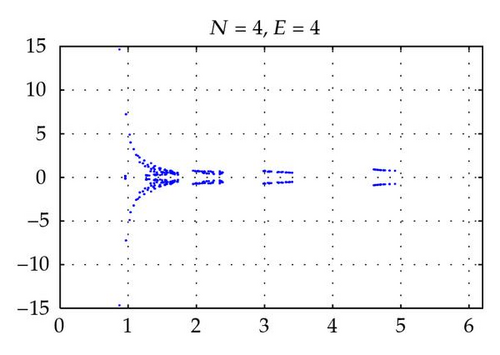
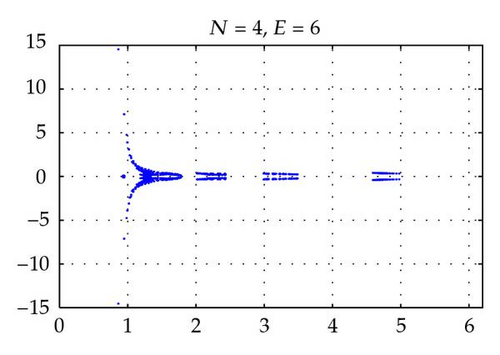
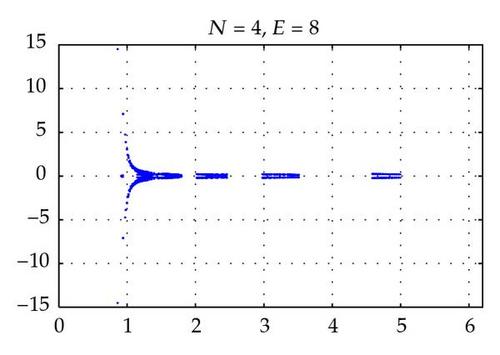
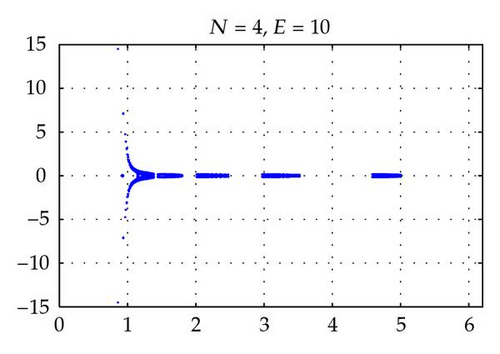
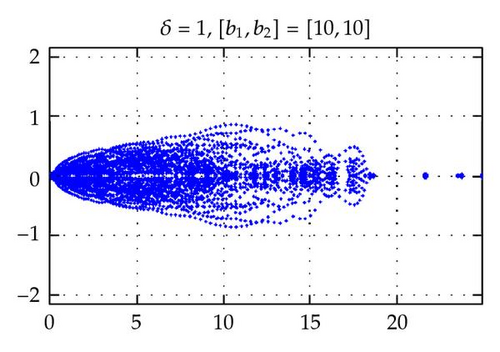
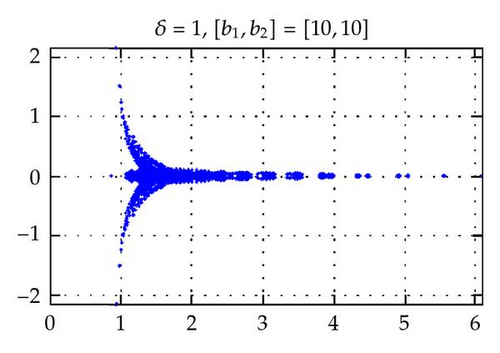
By choosing the convection coefficient b = [10,10]T, in Figure 6, the distributions of eigenvalues of (left) and (right) are presented for penalty parameters δ = 1,10−3 to examine their dependence. In this figure, we see that the distributions of eigenvalues (both real and imaginary part) of are strongly dependent on δ. The real parts of such eigenvalues are increased in proportion to 1/δ. On the other hand, as predicted by Theorem 3.4, the real parts of the eigenvalues of are positive and uniformly bounded away from 0. Moreover, the real parts are not dependent on δ and b (see Figures 2–6), and their moduli are uniformly bounded. The numerical results show that the imaginary parts of the eigenvalues are bounded by some constants which are dependent on δ and b. These phenomena support the theory proved in Theorem 3.4.

Details are in the caption following the image
Figure 6 (a)
Open in figure viewerPowerPoint
The eigenvalues of (left) and (right) for δ = 1 (top) and δ = 10−3 (bottom) when b = [10,10]T and N = 12, E = 4.
Details are in the caption following the image
Figure 6 (b)
Open in figure viewerPowerPoint
The eigenvalues of (left) and (right) for δ = 1 (top) and δ = 10−3 (bottom) when b = [10,10]T and N = 12, E = 4.
Details are in the caption following the image
Figure 6 (c)
Open in figure viewerPowerPoint
The eigenvalues of (left) and (right) for δ = 1 (top) and δ = 10−3 (bottom) when b = [10,10]T and N = 12, E = 4.
Details are in the caption following the image
Figure 6 (d)
Open in figure viewerPowerPoint
The eigenvalues of (left) and (right) for δ = 1 (top) and δ = 10−3 (bottom) when b = [10,10]T and N = 12, E = 4.

5. Concluding Remarks

An optimal control problem subject to an elliptic partial differential equation yields coupled elliptic differential equations (1.1). Any kind of discretizations leads to a nonsymmetric linear system which may require Krylov subspace methods to solve the system. In this paper, the spectral element discretization is chosen because it is very accurate and popular, but the resulting linear systems have large condition numbers. This situation now becomes one of disadvantages if one aims at a fast and efficient numerical simulation for an optimal control problem subject to even a simple elliptic differential equation. To overcome such a disadvantage, the lower-order finite element preconditioner is proposed so that the preconditioned linear system has uniformly bounded condition numbers independent of the degrees of polynomials and the mesh sizes. One may also take various degrees of polynomials on subintervals with different mesh sizes. In this case, similar results can be obtained without any difficulties. This kind of finite element preconditioner may be used for an optimal control problem subject to Stokes flow (see, e.g., [13]).

Acknowledgments

The authors would like to thank Professor. Gunzburg for his kind advice to improve this paper. This work was supported by KRF under contract no. C00094.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.