Volume 2012, Issue 1 237430

Research Article

Open Access

Robust Exponential Stability for LPD Discrete-Time System with Interval Time-Varying Delay

Kanit Mukdasai,

Corresponding Author

Kanit Mukdasai

[email protected]

Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand kku.ac.th

Centre of Excellence in Mathematics, CHE, Si Ayuthaya Road, Bangkok 10400, Thailand

Search for more papers by this author

Kanit Mukdasai,

Corresponding Author

Kanit Mukdasai

[email protected]

Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen 40002, Thailand kku.ac.th

Centre of Excellence in Mathematics, CHE, Si Ayuthaya Road, Bangkok 10400, Thailand

Search for more papers by this author

First published: 28 August 2012

https://doi.org/10.1155/2012/237430

Citations: 5

Academic Editor: B. V. Rathish Kumar

Share a link

Email
Wechat
Bluesky

Abstract

This paper investigates the problem of robust exponential stability for uncertain linear-parameter dependent (LPD) discrete-time system with delay. The delay is of an interval type, which means that both lower and upper bounds for the time-varying delay are available. The uncertainty under consideration is norm-bounded uncertainty. Based on combination of the linear matrix inequality (LMI) technique and the use of suitable Lyapunov-Krasovskii functional, new sufficient conditions for the robust exponential stability are obtained in terms of LMI. Numerical examples are given to demonstrate the effectiveness and less conservativeness of the proposed methods.

1. Introduction

Over the past decades, the problem of stability analysis of delay discrete-time systems has been widely investigated by many researchers. Because the existence of time delay is frequent, a source of oscillation instability performances degradation of systems. Stability criteria for discrete-time systems with time delay is generally divided into two classes: delay-independent ones and delay-dependent ones. Delay-independent stability criteria tend to be more conservative, especially for small-size delay; such criteria do not give any information on the size of the delay. On the other hand, delay-dependent stability criteria is concerned with the size of the delay and usually provide a maximal delay size. Moreover, robust stability of linear continuous-time and discrete-time systems subject to time-invariant parametric uncertainty has received considerable attention. An important class of linear time-invariant parametric uncertain system is linear parameter-dependent (LPD) system in which the uncertain state matrices are in the polytope consisting of all convex combination of known matrices. To address this problem, several results have been obtained in terms of sufficient (or necessary and sufficient) conditions; see [1–15] and references cited therein. Most of these conditions have been obtained via the Lyapunov theory approaches in which parameter dependent Lyapunov functions have been employed. These conditions are always expressed in terms of linear matrix inequalities (LMIs) which can be solved numerically by using available tools such as LMI toolbox in MATLAB. The results have been obtained for robust stability for LPD systems in which time delay occur in state variable such as [6, 11, 14] present sufficient conditions for robust stability of LPD continuous-time system with delays. However, a few results have been obtained for robust stability for LPD discrete-time systems with delay.

In this paper, we deal with the problem of robust exponential stability for uncertain LPD discrete-time system with interval time-varying delay. Combined with the linear matrix inequality technique and the use of suitable Lyapunov-Krasovskii functional, new sufficient conditions for the robust exponential stability are obtained in terms of LMI. Finally, numerical examples have demonstrated the effectiveness of the criteria.

2. Problem Formulation and Preliminaries

We introduce some notations and definitions that will be used throughout the paper. ℤ⁺ denotes the set of non negative integer numbers; ℝⁿ denotes the n-dimensional space with the vector norm ∥·∥; ∥x∥ denotes the Euclidean vector norm of x ∈ ℝⁿ; that is, ∥x∥² = x^Tx; M^n×r denotes the space of all matrices of (n × r)-dimensions; A^T denotes transpose of the Matrix A; A is symmetric if A = A^T; I denotes the identity matrix; λ(A) denotes the set of all eigenvalues of A; λ_max(A) = max {Reλ : λ ∈ λ(A)}; Matrix A is called semi positive definite (A ≥ 0) if x^TAx ≥ 0, for all x ∈ ℝⁿ; A is positive definite (A > 0) if x^TAx > 0 for all x ≠ 0; Matrix B is called semi-negative definite (B ≤ 0) if x^TBx ≤ 0, for all x ∈ ℝⁿ; B is negative definite (B < 0) if x^TBx < 0 for all x ≠ 0; A > B means A − B > 0; A ≥ B means A − B ≥ 0; * represents the elements below the main diagonal of a symmetric matrix.

Consider the following uncertain LPD discrete-time system with interval time-varying delay in the state

(2.1)

where k ∈ ℤ⁺, x(k) ∈ ℝⁿ is the system state and ϕ(s) is a initial value at s. A(α), B(α) ∈ M^n×n are uncertain matrices belonging to the polytope of the form

(2.2)

ΔA(k) and ΔB(k) are unknown matrices representing time-varying parameter uncertainties, we assumed to be of the form

(2.3)

The class of parametric uncertainties Δ(k), which satisfies

(2.4)

is said to be admissible where J is a known matrix satisfying

(2.5)

and F(k) is uncertain matrix satisfying

(2.6)

In addition, we assume that the time-varying delay h(k) is upper and lower bounded. It satisfies the following assumption of the form

(2.7)

where h₁ and h₂ are known positive integers.

Definition 2.1. The uncertain LPD discrete-time-delayed system in (2.1) is said to be robustly exponentially stable if there exist constant scalars 0 < a < 1 and b > 0 such that

(2.8)

for all admissible uncertainties.

Lemma 2.2 (see [5] Schur complement lemma.)Given constant matrices X, Y, Z of appropriate dimensions with Y > 0. Then X + Z^TY⁻¹Z < 0 if and only if

(2.9)

Lemma 2.3 (see [2].)Given constant matrices M₁, M₂, and M₃ of appropriate dimensions with . Then,

(2.10)

where Δ(k) = F(k)[I − JF(k)] ⁻¹, F(k) ^TF(k) ≤ I, for all k ∈ ℤ⁺ if and only if

(2.11)

for some scalar ϵ > 0.

3. Main Results

In this section, we present our main results on the robust exponential stability criteria for uncertain LPD discrete-time system with interval time-varying delays. We introduce the following notation for later use:

(3.1)

Lemma 3.1. For any in (3.1), P(α) and Q(α) given by

(3.2)

are parameter-dependent positive definite Lyapunov matrices such that

(3.3)

if and only if

(3.4)

Proof. Consider

(3.5)

We assume that

(3.6)

Using Lemma 2.2, we obtain

(3.7)

We rewrite the latter inequality as

(3.8)

Using Lemma 2.3, inequality (3.8) holds if and only if there exists ϵ > 0 such that

(3.9)

If we apply to (3.9), then we obtain

(3.10)

Premultiplying (3.10) by diag{I, I, P(α), I, I} and postmultiplying by diag{I, I, P(α), I, I}, we get that (3.4) and the lemma is proved.

Lemma 3.2. If there exist positive definite symmetric matrices P_i, Q_i, i = 1,2, …, N, and positive real numbers ϵ, ζ such that

(3.11)

then, for any

in (3.1), P(α) and Q(α) are parameter-dependent positive definite Lyapunov matrices in Lemma 3.1 such that (3.4) holds.

Proof. Consider

(3.12)

Using the fact that

, we obtain the following identities:

(3.13)

Then, it follows from (3.11), (3.12), and (3.13) that (3.4) holds. The proof of the lemma is complete.

Theorem 3.3. The system (2.1) is robustly exponentially stable if the LMI conditions (3.11) are feasible.

Proof. Consider the following Lyapunov-Krasovskii function for system (2.1) of the form

(3.14)

where

(3.15)

A Lyapunov-Krasovskii difference for the system (2.1) is defined as

(3.16)

Taking the difference of V₁(x(k)) and V₂(x(k)), the increments of V₁(x(k)) and V₂(x(k)) are

(3.17)

(3.18)

Form h(k) ≥ h₁, the two last terms of the right-hand side of the latter equality yield

(3.19)

Thus, we obtain

(3.20)

The increment of V₃(x(k)) is easily computed as

(3.21)

It is easy to see that

(3.22)

for simplicity, we let x(k − h(k)) = x_k−h. Since, h(k) ≤ h₂, we obtain that

(3.23)

Therefore, we conclude that

(3.24)

It follows form (3.24) that

(3.25)

where

and Y^T = [x(k) ^T x(k − h(k)) ^T]. By (3.11), (3.25), and Lemma 3.1, and 3.2, we obtain

(3.26)

where ω > 0. By (3.14), it is easy to see that

(3.27)

where

(3.28)

It can be shown that there always exists a scalar θ > 1 satisfying

(3.29)

For any scalar θ > 1, it follows from (3.26) and (3.27) that

(3.30)

where

(3.31)

Therefore, for any integer T ≥ h₂ + 1, summing up both sides of (3.30) from 0 to T − 1 gives

(3.32)

For h₂ ≥ 1,

(3.33)

From (3.32) and (3.33), we obtain

(3.34)

Observe

(3.35)

Then, it follows from (3.29), (3.33), and (3.35) that

(3.36)

By Definition 2.1, this means that the system (2.1) is robustly exponentially stable. The proof of the theorem is complete.

4. Numerical Example

Example 4.1. Consider the following uncertain LPD discrete-time system with time-varying delays (2.1) where h(k) = 2 + cos (kπ/2), that is, h₁ = 1, h₂ = 3 and

(4.1)

and

. By using LMI Toolbox in MATLAB, we use condition (3.11) in Theorem 3.3 for this example. The solutions of LMI verify as follows of the form ϵ = 1,

, and

(see Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The simulation solution of the states x₁(k) and x₂(k) in Example 4.1 for uncertain LPD discrete-time delayed system with initial conditions x₁(k) = 2 and x₂(k) = 4, k = −3, −2, −1,0, and α₁ = α₂ = 1/2 by using the method of Runge-Kutta order 4(h = 0.01) with Matlab.

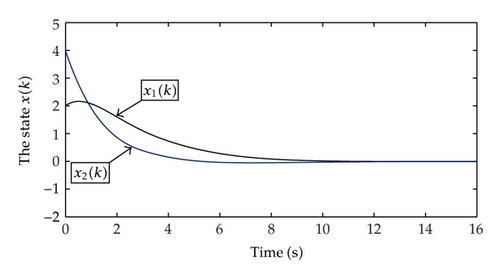
Example 4.2. Consider the following the LPD discrete-time system with time-varying delays (2.1) where, ΔA(k) = ΔB(k) = 0 with

(4.2)

Table 1 lists the comparison of the upper-bound delay for asymptotic stability of system (2.1) where ΔA(k) = ΔB(k) = 0 by different method. We apply Theorem 3.3 and see from Table 1 that our result is superior to those in [7, Theorem 3.2].

Table 1. Comparison of the maximum allowed time delay h₂.

Methods	h₂ (h₁ = 2)	h₂ (h₁ = 4)	h₂ (h₁ = 5)	h₂ (h₁ = 7)
Liu et al. [7] 2006	2	4	5	7
Our results	4	6	7	9

Acknowledgments

This work was supported by the Thailand Research Fund (TRF), the Office of the Higher Education Commission (OHEC), and the Khon Kaen University (Grant number MRG5580006), and the author would like to thank his advisor Associate Professor Dr. Piyapong Niamsup from the Department of Mathematics, Faculty of Science, Chiang Mai University, Chiang Mai, Thailand.

References

1 Botmart T. and Niamsup P., Robust exponential stability and stabilizability of linear parameter dependent systems with delays, Applied Mathematics and Computation. (2010) 217, no. 6, 2551–2566, https://doi.org/10.1016/j.amc.2010.07.068, 2733699, ZBL1207.93087.
10.1016/j.amc.2010.07.068
Web of Science® Google Scholar
2 Cui B. T. and Hua M. G., Robust passive control for uncertain discrete-time systems with time-varying delays, Chaos, Solitons and Fractals. (2006) 29, no. 2, 331–341, https://doi.org/10.1016/j.chaos.2005.08.039, 2211469, ZBL1147.93034.
10.1016/j.chaos.2005.08.039
Web of Science® Google Scholar
3 Fang M., Delay-dependent stability analysis for discrete singular systems with time-varying delays, Acta Automatica Sinica. (2010) 36, no. 5, 751–755, https://doi.org/10.3724/SP.J.1004.2010.00751, 2759582.
10.3724/SP.J.1004.2010.00751
Google Scholar
4 Fridman E. and Shaked U., Parameter dependent stability and stabilization of uncertain time-delay systems, IEEE Transactions on Automatic Control. (2003) 48, no. 5, 861–866, https://doi.org/10.1109/TAC.2003.811269, 1980597.
10.1109/TAC.2003.811269
Web of Science® Google Scholar
5 Gu K., Kharitonov V. L., and Chen J., Stability of Time-Delay Systems, 2003, Birkhäuser, Berlin, Germany.
10.1007/978-1-4612-0039-0
Google Scholar
6 He Y., Wu M., She J. H., and Liu G. P., Parameter-dependent Lyapunov functional for stability of time-delay systems with polytopic-type uncertainties, IEEE Transactions on Automatic Control. (2004) 49, no. 5, 828–832, https://doi.org/10.1109/TAC.2004.828317, 2057826.
10.1109/TAC.2004.828317
Web of Science® Google Scholar
7 Liu X., Martin R., Wu M., and Tang M., Delay-dependent robust stabilisation of discrete-time systems with time-varying delay, IEE Proceedings—Control Theory and Applications. (2006) 153, no. 6, 689–702, https://doi.org/10.1049/ip%2Dcta:20050223, 2350703.
10.1049/ip-cta:20050223
Web of Science® Google Scholar
8 Mao W. J., An LMI approach to D-stability and D-stabilization of linear discrete singular system with state delay, Applied Mathematics and Computation. (2011) 218, no. 5, 1694–1704, https://doi.org/10.1016/j.amc.2011.06.048, 2831392.
10.1016/j.amc.2011.06.048
Web of Science® Google Scholar
9 Mao W. J. and Chu J., D-stability and D-stabilization of linear discrete time-delay systems with polytopic uncertainties, Automatica. (2009) 45, no. 3, 842–846, https://doi.org/10.1016/j.automatica.2008.11.003, 2527274.
10.1016/j.automatica.2008.11.003
CAS Web of Science® Google Scholar
10 Mukdasai K. and Niamsup P., Robust stability of discrete-time linear parameter dependent system with delay, Thai Journal of Mathematics. (2010) 8, no. 4, 11–20, 2763648, ZBL1238.93077.
Google Scholar
11 Niamsup P. and Phat V. N., H_∞ control for nonlinear time-varying delay systems with convex polytopic uncertainties, Nonlinear Analysis. (2010) 72, no. 11, 4254–4263, https://doi.org/10.1016/j.na.2010.02.001, 2606782, ZBL1189.93041.
10.1016/j.na.2010.02.001
Web of Science® Google Scholar
12 De la Sen M., Robust stabilization of a class of polytopic linear time-varying continuous systems under point delays and saturating controls, Applied Mathematics and Computation. (2006) 181, no. 1, 73–83, https://doi.org/10.1016/j.amc.2006.01.013, 2270471, ZBL1143.93021.
10.1016/j.amc.2006.01.013
Web of Science® Google Scholar
13 Wu Z. G., Shi P., Su H., and Chu J., Delay-dependent exponential stability analysis for discretetime switched neural networks with time-varying delay, Neurocomputing. (2011) 74, no. 10, 1626–1631.
10.1016/j.neucom.2011.01.015
Web of Science® Google Scholar
14 Xia Y. and Jia Y., Robust stability functionals of state delayed systems with polytopic type uncertainties via parameter-dependent Lyapunov functions, International Journal of Control. (2002) 75, no. 16-17, 1427–1434, https://doi.org/10.1080/0020717021000023834, 1956388, ZBL1078.93054.
10.1080/0020717021000023834
Web of Science® Google Scholar
15 Zhang W. A. and Yu L., Stability analysis for discrete-time switched time-delay systems, Automatica. (2009) 45, no. 10, 2265–2271.
10.1016/j.automatica.2009.05.027
Web of Science® Google Scholar

Citing Literature

All articles

Robust Exponential Stability for LPD Discrete-Time System with Interval Time-Varying Delay

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

4. Numerical Example

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Robust Exponential Stability for LPD Discrete-Time System with Interval Time-Varying Delay

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

4. Numerical Example

Acknowledgments

References

Citing Literature

Figures

References

Related

Information