By using the integral bifurcation method, we study the nonlinear K(m, n) equation for all possible values of m and n. Some new exact traveling wave solutions of explicit type, implicit type, and parametric type are obtained. These exact solutions include peculiar compacton solutions, singular periodic wave solutions, compacton-like periodic wave solutions, periodic blowup solutions, smooth soliton solutions, and kink and antikink wave solutions. The great parts of them are different from the results in existing references. In order to show their dynamic profiles intuitively, the solutions of K(n, n), K(2n − 1, n), K(3n − 2, n), K(4n − 3, n), and K(m, 1) equations are chosen to illustrate with the concrete features.

1. Introduction

In this paper, we will investigate some new traveling-wave phenomena of the following nonlinear dispersive K(m, n) equation [1]:

()

where m and n are integers and σ is a real parameter. This is a family of fully KdV equations. When σ = 1, (1.1) as a role of nonlinear dispersion in the formation of patterns in liquid drops was studied by Rosenau and Hyman [1]. In [2–6], the studies show that the model equation (1.1) supports compact solitary structure. In [3], especially Rosenau’s study shows that the branch + (i.e., σ = 1) supports compact solitary waves and the branch − (i.e., σ = −1) supports motion of kinks, solitons with spikes, cusps or peaks. In [7, 8], Wazwaz developed new solitary wave solutions of (1.1) with compact support and solitary patterns with cusps or infinite slopes under σ = ± 1, respectively. In [9], by using the extend decomposition method, Zhu and Lü obtained exact special solutions with solitary patterns for (1.1). In [10], by using homotopy perturbation method (HPM), Domairry et al. studied the (1.1); under particular cases, they obtained some numerical and exact compacton solutions of the nonlinear dispersive K(2,2) and K(3,3) equations with initial conditions. In [11], by variational iteration method, Tian and Yin obtained new solitary solutions for nonlinear dispersive equations K(m, n); under particular values of m and n, they obtained shock-peakon solutions for K(2,2) equation and shock-compacton solutions for K(3,3) equation. In [12], the nonlinear equation K(m, n) is studied by Wazwaz for all possible values of m and n. In [13], by using Adomian decomposition method, Zhu and Gao obtained new solitary-wave special solutions with compact support for (1.1). In [14], by using a new method which is different from the Adomian decomposition method, Shang studied (1.1) and obtained new exact solitary-wave solutions with compact. In [15, 16], 1-soliton solutions of the K(m, n) equation with generalized evolution are obtained by Biswas. In [17], the bright and dark soliton solutions for K(m, n) equation with t-dependent coefficients are obtained by Triki and Wazwaz, especially, when m = n, the K(n, n) equation was studied by many authors; see [18–24] and references cited therein. Defocusing branch, Deng et al. [25] obtained exact solitary and periodic traveling wave solutions of K(2,2) equation. Also, under some particular values of m and n, many authors considered some particular cases of K(m, n) equation. Ismail and Taha [26] implemented a finite difference method and a finite element method to study two types of equations K(2,2) and K(3,3). A single compacton as well as the interaction of compactons has been numerically studied. Then, Ismail [27] made an extension to the work in [26], applied a finite difference method on K(2,3) equation, and obtained numerical solutions of K(2,3) equation [28]. Frutos and Lopez-Marcos [29] presented a finite difference method for the numerical integration of K(2,2) equation. Zhou and Tian [30] studied soliton solution of K(2,2) equation. Xu and Tian [31] investigated the peaked wave solutions of K(2,2) equation. Zhou et al. [32] obtained kink-like wave solutions and antikink-like wave solutions of K(2,2) equation. He and Meng [33] obtain some new exact explicit peakon and smooth periodic wave solutions of the K(3,2) equation by the bifurcation method of planar systems and qualitative theory of polynomial differential system.

From the aforementioned references, and references cited therein, it has been shown that (1.1) is a very important physical and engineering model. This is a main reason for us to study it again. In this paper, by using the integral bifurcation method [34–36], we mainly investigate some new exact solutions such as explicit solutions of Jacobian elliptic function type with low-power, implicit solutions of Jacobian elliptic function type, periodic solutions of parametric type, and so forth. We also investigate some new traveling wave phenomena and their dynamic properties.

The rest of this paper is organized as follows. In Section 2, we will derive the equivalent two-dimensional planar system of (1.1) and its first integral. In Section 3, by using the integral bifurcation method, we will obtain some new traveling wave solutions and discuss their dynamic properties; some phenomena of new traveling waves are illustrated with the concrete features.

2. The Equivalent Two-Dimensional Planar System to (1.1) and Its First Integral Equations

We make a transformation u(t, x) = ϕ(ξ) with ξ = x − vt, where the v is a nonzero constant as wave velocity. Thus, (1.1) can be reduced to the following ODE:

()

Integrating (2.1) once and setting the integral constant as zero yields

()

Let ϕ^′ = (dϕ/dξ) = y. The equation (2.2) can be reduced to a 2D planar system:

()

where ϕ ≠ 0. Obviously, the solutions of (2.2) include the solutions of (2.3) and constant solution ϕ = 0. We notice that the second equation in (2.3) is not continuous when ϕ = 0; that is, the function ϕ^′′(ξ) is not defined by the singular line ϕ = 0. Therefore, we make the following transformation:

()

where τ is a free parameter. Under the transformation (2.4), (2.3), and ϕ = 0 combine to make one 2D system as follows:

()

Clearly, (2.5) is equivalent to (2.2). It is easy to know that (2.3) and (2.5) have the same first integral as follows:

()

where h is an integral constant. From (2.6), we define a function as follows:

()

It is easy to verify that (2.5) satisfies

()

Therefore, (2.5) is a Hamiltonian system and 1/2ϕⁿ⁻¹ is an integral factor. In fact, (2.7) can be rewritten as the form H = E + T, where E = (1/2)My² = (1/2)M(ϕ^′) ² and T = (2σ/(n + m))ϕ^m+n − (2v/(n + 1))ϕⁿ⁺¹ with M = 2nϕ²ⁿ⁻².E denotes kinetic energy, and T denotes potential energy. Especially, when n = 1, M becomes a constant 2. In this case, the kinetic energy E only depends on movement velocity ϕ^′ of particle; it does not depend on potential function ϕ. So, according to Theorem 3.2 in [37], it is easy to know that (2.5) is a stable and nonsingular system when n = 1; in this case its solutions have not singular characters. When n > 1, (2.5) becomes a singular system; in this case some solutions of (2.5) have singular characters.

For the equilibrium points of the system (2.5), we have the following conclusion.

Case 1. When m is even number, (2.5) has two equilibrium points O(0,0) and A₀((v/σ)^1/(m−1), 0). From (2.7), we obtain

()

Case 2. When m is odd number and σv > 0, (2.5) has three equilibrium points O(0,0) and A_1,2(±(v/σ)^1/(m−1), 0). From (2.7), we also obtain h_O = H(0,0) = 0 and

()

Obviously, if n is odd, then

. If n is even, then

. Then h_O = H(0,0) = 0 whether m is odd number or even number.

3. Exact Solutions of Explicit Type, Implicit Type, and Parametric Type and Their Properties

3.1. Exact Solutions and Their Properties of (1.1) under h = h_O

Taking h = h_O = 0, (2.6) can be reduced to

()

(i)
When m = n > 1, (3.1) can be rewritten as

()

Substituting (3.2) into the first expression in (2.5) yields

()

Noticing that equation

has two roots ϕ = 0 and ϕ = [2nv/(n + 1)σ] ^1/(n−1), we take ([2nv/(n + 1)σ] ^1/(n−1), 0) as the initial value. Using this initial value, integrating (3.2) yields

()

After completing the aforementioned integral, we solve this equation; thus we obtain

()

Substituting (3.5) into (2.4), then integrating it yields

()

Thus, we respectively obtain a periodic wave solution and solitary wave solution of parametric type for the equation K(n, n) as follows:

()

On the other hand, (3.1) can be rewritten as

()

Using ([2nv/(n + 1)σ] ^1/(n−1), 0) as the initial value, substituting (3.9) into the first expression in (2.3) directly, we obtain an integral equation as follows:

()

Completing the aforementioned integral equation, then solving it, we obtain a periodic solution and a hyperbolic function solution as follows:

()

Obviously, the solution (3.7) is equal to the solution (3.11); also the solution (3.8) is equal to the solution (3.12). Similarly, taking the (0,0) as initial value, substituting (3.9) into the first expression in (2.3), then integrating them, we obtain another periodic solution and another hyperbolic function solution of K(n, n) equation as follows.

()

In fact, the solutions (3.11) and (3.13) have been appeared in [35], so we do not list similar solutions anymore at here. Next, we discuss a interesting problem as follows.

When σ > 0, from (3.11) and (3.13), we can construct two compacton solutions as follows:

()

The shape of compacton solutions (3.15) and (3.16) changes gradually as the value of parameter n increases. For example, when n = 2,15,400, respectively, the shapes of compacton solution (3.15) are shown in Figure 1.

(ii)
When n = 1, m > 1, (3.1) can be directly reduced to

()

Equation (3.17) is a nonsingular equation. Using ([2σ/(m + 1)v] ⁿ⁻¹, 0) as initial value and then substituting (3.17) into the first expression in (2.3) directly, we obtain a smooth solitary wave solution and a periodic wave solution of K(m, 1) equation as follows:

()

Also, the shape of solitary wave solution (3.18) changes gradually as the value of parameter m increases. When m = 2,20,200, respectively, its shapes of compacton solution (3.18) are shown in Figure 2.

(iii)
When n is even number and m = 2n − 1, (3.1) can be reduced to

()

It is easy to know that (2nv/(n + 1))ϕⁿ⁻¹ − (2nσ/(3n − 1))ϕ³⁽ⁿ⁻¹⁾ = 0 has three roots ϕ = 0 and ϕ = α, γ with

when σv > 0. In fact, γ = −α. Using these three roots as initial value, respectively, then substituting (3.20) into the first expression in (2.3), we obtain three integral equations as follows:

()

Completing the previous three integral equations, then solving them, we obtain three periodic solutions of Jacobian elliptic function for K(2n − 1, n) equation as follows:

()

Details are in the caption following the image — **Figure 1 (a) n = 2**
Open in figure viewer PowerPoint

The solution u in (3.15) shows a shape of compacton for parameters v = 2, and σ = 1.

The solutions (3.22) and (3.24) show two shapes of periodic wave with blowup form, which are shown in Figures 3(a) and 3(c). The solution (3.23) shows a shape of periodic cusp wave, which is shown in Figure 3(b).

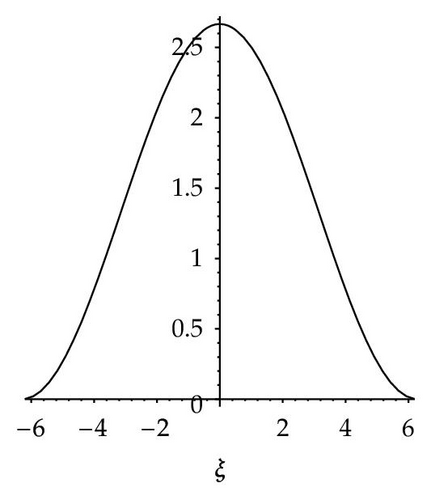
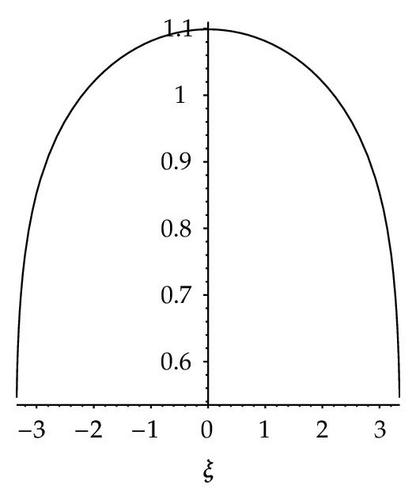
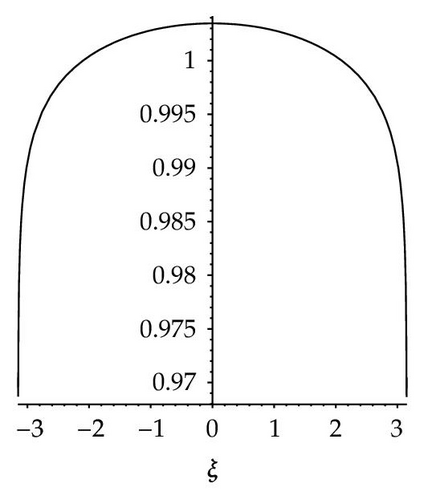
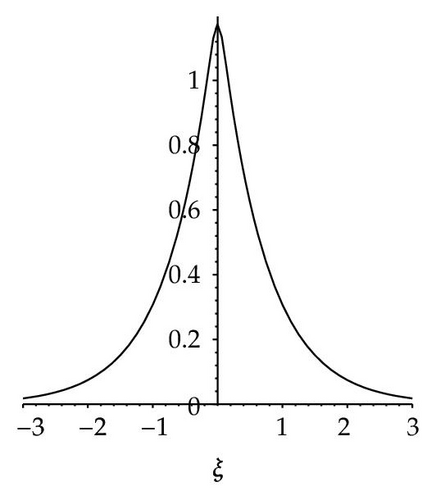
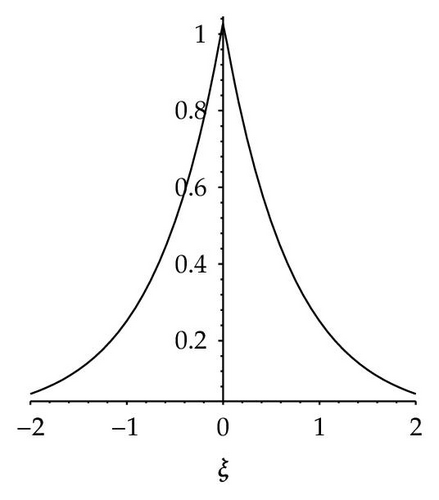
(iv)
When m = 3n − 2, n > 1, (3.1) can be directly reduced to

()

It is easy to know that the function

, where

. Using (a^1/(n−1), 0) and (0,0) as initial values, respectively, substituting (3.25) into the first expression in (2.3), we obtain four elliptic integral equations as follows.

(1)
When σ > 0, v > 0,

()

(2)
When σ > 0, v < 0,

()

(3)
When σ < 0, v < 0,

()

(4)
When σ < 0, v > 0,

()

Corresponding to (3.26), (3.27), (3.28), and (3.29), respectively, we obtain four periodic solutions of elliptic function type for K(3n − 2, n) equation as follows:

()

where

with

given previously.

The solution (3.30) shows a shape of periodic wave with blowup form, which is shown in Figure 4(a). The solution (3.31) shows s shape of compacton-like periodic wave, which is shown in Figure 4(b). The profile of solution (3.32) is similar to that of solution (3.30). Also the profile of solution (3.33) is similar to that of solution (3.31). So we omit the graphs of their profiles here.

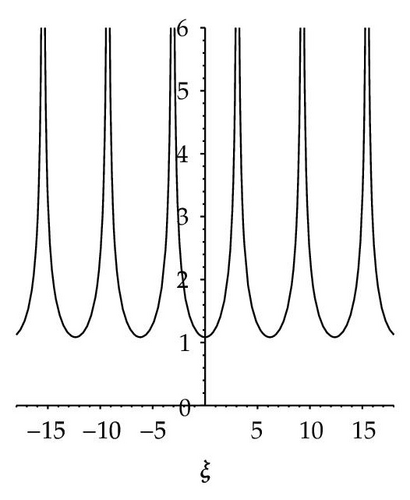
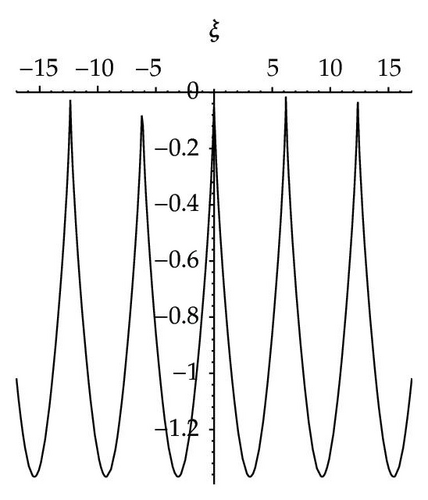
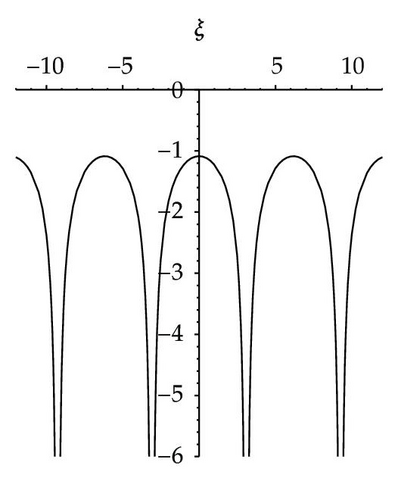
(v)
When m = (k − 1)n − k + 2, n > 1, k > 4, (3.1) can be directly reduced to

()

Suppose that ϕ₀ = ϕ(0) is one of roots for equation (2nv/(n + 1))ϕⁿ⁻¹ − (2nσ/(k(n − 1) + 2))ϕ^k(n−1) = 0. Clearly, the 0 is its one root. Anyone solution of K((k − 1)n − k + 2, n) equation can be obtained theoretically from the following integral equations:

()

The left integral of (3.35) is called hyperelliptic integral for ϕⁿ⁻¹ when the degree k is greater than four. Let ϕⁿ⁻¹ = z. Thus, (3.35) can be reduced to

()

In fact, we cannot obtain exact solutions by (3.36) when the degree k is grater than five. But we can obtain exact solutions by (3.36) when

, and σ < 0. Under these particular conditions, taking

as initial value, (3.36) becomes

()

Let

. We obtain

and 0 < Z ≤ 1. Thus, (3.37) can be transformed to

()

Completing (3.38) and refunded the variable z = ϕⁿ⁻¹, we obtain two implicit solutions of elliptic function type for K(4n − 3, n) equation as follows:

()

where

. The solutions also can be rewritten as

()

where the function F(φ, k) = Elliptic F(φ, k) is the incomplete Elliptic integral of the first kind.

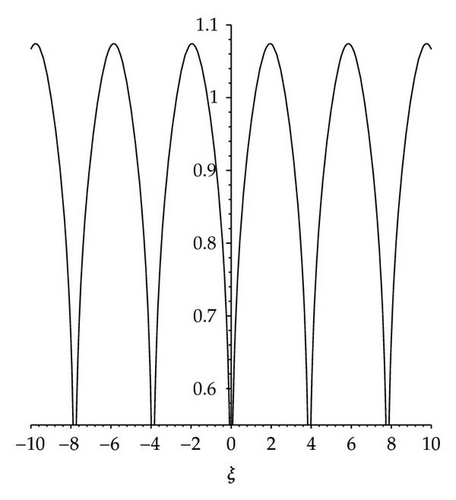
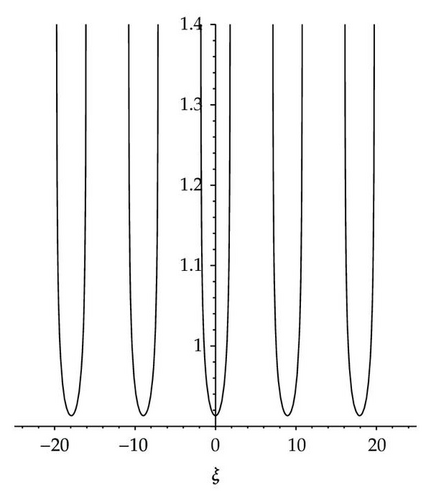
The two solutions in (3.40) are asymptotically stable. Under ,ϕ → 0 as ξ → ∞. Under , ϕ → 0 as ξ → −∞. The graphs of their profiles are shown in Figure 5.

3.2. Exact Solutions and Their Properties of (1.1) under h ≠ 0

In this subsection, under the conditions

, we will investigate exact solutions of (1.1) and discuss their properties. When h ≠ 0, (2.6) can be reduced to

()

Substituting (3.41) into the first expression of (2.3) yields

()

where ϕ_* is one of roots for equation h + (2nv/(n + 1))ϕⁿ⁺¹ − (2nσ/(n + m))ϕ^n+m = 0. However we cannot obtain any exact solutions by (3.42) when the degrees m and n are more great, because we cannot obtain coincidence relationship among different degrees n, n + 1 and n + m. But, we can always obtain some exact solutions when the degree m + n is not greater than four. For example, by using (3.42) directly, we can also obtain many exact solutions of K(2,1) and K(3,1) equations; see the next computation and discussion.

(i)
If m = n = 2, then (3.41) can be reduced to

()

Taking

as Hamiltonian quantity, substituting (3.43) and m = n = 2 into the first expression of (2.5) yields

()

Then −(v⁴/6σ³) + (4v/3)ϕ³ − σϕ⁴ = 0 has four roots, two real roots, and two complex roots as follows:

()

with

(1)
When σ > 0 and a > ϕ > b, taking b as initial value, then integrating (3.44) yields

()

Solving the aforementioned integral equation yields

()

where α₁ = (bA − aB)/(aB + bA), α = (A − B)/(A + B) and

with

and

Substituting (3.47) and n = 2 into (2.4) yields

()

where

, the Π(φ, α²/(α² − 1), k) is an elliptic integral of the third kind, and the function f₁ satisfies the following three cases, respectively:

In the previous three cases,

. Thus, by using (3.47) and (3.48), we obtain a parametric solution of Jacobian elliptic function for K(2,2) equation as follows:

()

(2)
When σ < 0 and b < a < ϕ < ∞, taking a as initial value, integrating (3.44) yields

()

Solving the aforementioned integral equation yields

()

where

and A and B are given in case (1). Substituting (3.51) and n = 2 into (2.4) yields

()

where

is an elliptic integral of the third kind, and the function

satisfies the following three cases, respectively:

In the previous three cases,

. Thus, by using (3.51) and (3.52), we obtain another parametric solution of Jacobian elliptic function for K(2,2) equation as follows:

()

In addition, when h < −v⁴/6σ³ , h + (4v/3)ϕ³ − σϕ⁴ = 0 has four complex roots; in this case, we cannot obtain any useful results for K(2,2) equation. When h > −v⁴/6σ³ , the case is very similar to (3.52); that is, the equation h + (4v/3)ϕ³ − σϕ⁴ = 0 has two real roots and two complex roots. So we omit the discussions for these parts of results.

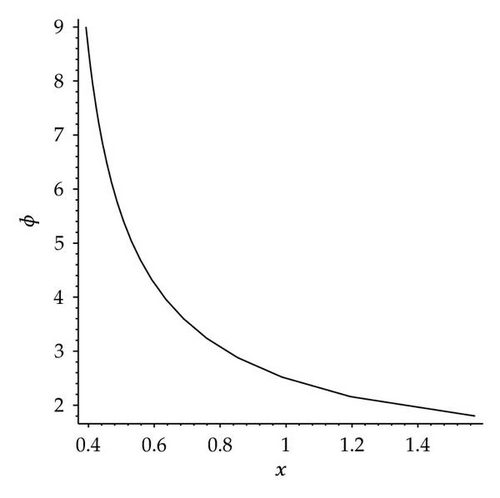
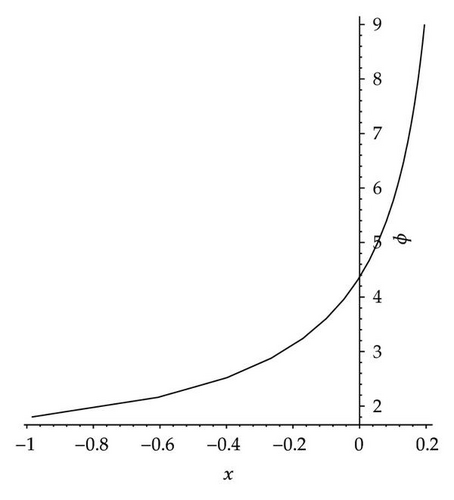
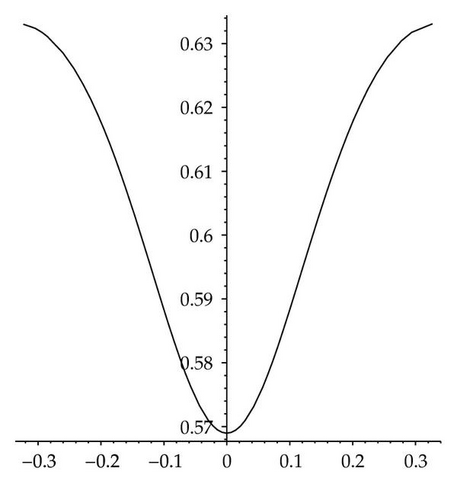
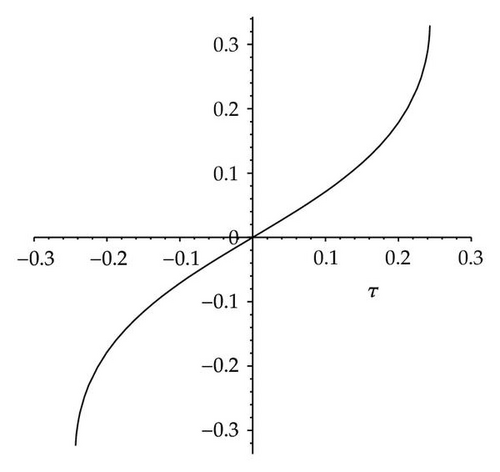
In order to describe the dynamic properties of the traveling wave solutions (3.49) and (3.53) intuitively, as an example, we draw profile figure of solution (3.53) by using the software Maple, when v = 4, and σ = −2, see Figure 6(a).

Figure 6(a) shows a shape of peculiar compacton wave; its independent variable ξ is bounded region (i.e., |ξ | < α₁ + 1); see Figure 6(b). From Figure 6(a), we find that its shape is very similar to that of the solitary wave, but it is not solitary wave because when |ξ | ≥ α₁ + 1, u ≡ 0. So, this is a new compacton.

(ii)
Under m = 2, n = 1, taking as Hamiltonian quantity, (3.42) can be reduced to

()

where ϕ_* is one of roots for the equation −(v³/3σ² ) + vϕ² − (2σ/3)ϕ³ = 0. Clearly, this equation has three real roots, one single root −v/2σ and two double roots v/σ, v/σ. If σ > 0, then the function

; if σ < 0, then the function

. In these two conditions, taking ϕ_* = −(v/2σ) as initial value and completing the (3.54), we obtain a periodic solution and a solitary wave solutions for K(2,1) as follows:

()

Similarly, taking ϕ_* = v/σ as initial value, we obtain two periodic solutions for K(2,1) as follows:

()

(iii)
Under m = 2, n = 1, taking arbitrary constant h as Hamiltonian quantity, (3.42) can be reduced to

()

where p = −3v/2σ, q = −3h/2σ. Write

. It is easy to know that Δ = 0 as

; this case is same as case (ii). So, we only discuss the case Δ < 0 in the next.

When h, σ, and v satisfy Δ < 0, ϕ³ + pϕ² + q = 0 has three real roots z₁, z₂, and z₃ such as

with

and v/σ > 0. Under these conditions, taking the z₁, z₂, and z₃ as initial values replacing ϕ_*, respectively, (3.57) can be reduced to the following three integral equations:

()

Integrating the (3.58), then solving them, respectively, we obtain three periodic solutions of elliptic function type for K(2,1) as follows:

()

where

, and

(iv)
When m = 3, n = 1, taking the constant as Hamiltonian quantity, (3.42) can be reduced to

()

Clearly, (v/σ) − ϕ² = 0 has two real roots

. Taking

as initial value, solving (3.62), we obtain a kink wave solution and an antikink wave solution for K(3,1) as follows:

()

where v < 0 shows that the waves defined by (3.63) are reverse traveling waves.

(v)
Under m = 3, n = 1, taking arbitrary constant h as Hamiltonian quantity and h ≠ −(v²/2σ), (3.42) can be reduced to

()

Clearly, ϕ⁴ − (2v/σ)ϕ² − (2h/σ) = 0 has four real roots

if σ < 0, v < 0, and 0 < h < −(v²/2σ) or σ > 0, v > 0, and − (v²/2σ) < h < 0; it has two real roots

and two complex roots

if σ < 0, v < 0, and h < 0 or σ > 0, v > 0, and h > 0; it has not any real roots if σ < 0, v < 0, and h > −v²/2σ or σ > 0, v > 0, and h < −v²/2σ.

(1)
Under the conditions σ < 0, v < 0, and 0 < h < −v²/2σ or σ > 0, v > 0, and − v²/2σ < h < 0, taking ϕ_* = r₁ as an initial value, (3.64) and (3.65) can be reduced to

()

where r₁ > r₂ > r₃ > r₄. Solving the integral equations (3.66), we obtain two periodic solutions of Jacobian elliptic function for K(3,1) equation as follows:

()

where

()

where

. The case for taking ϕ_* = r₂, r₃, r₄ as initial values can be similarly discussed; here we omit these discussions because these results are very similar to the solutions (3.67) and (3.68).

(2)
Under the conditions σ < 0, v < 0, and h < 0 or σ > 0, v > 0, and h > 0, respectively taking ϕ_* = s₁, s₂ as initial value, (3.64) and (3.65) can be reduced to

()

Solving the aforementioned two integral equations, we obtain two periodic solutions of Jacobian elliptic function for K(3,1) equation as follows:

()

where

with

, and s₁ and s₂ are given previously.

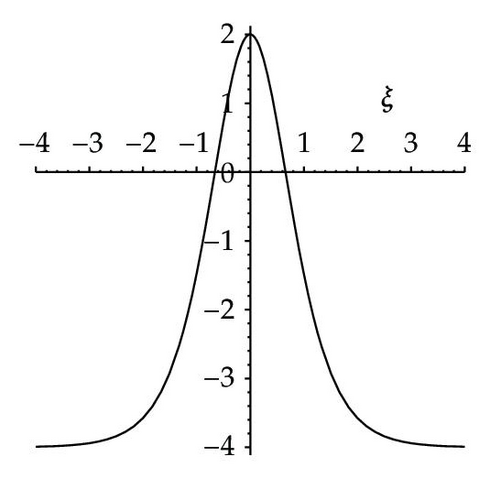
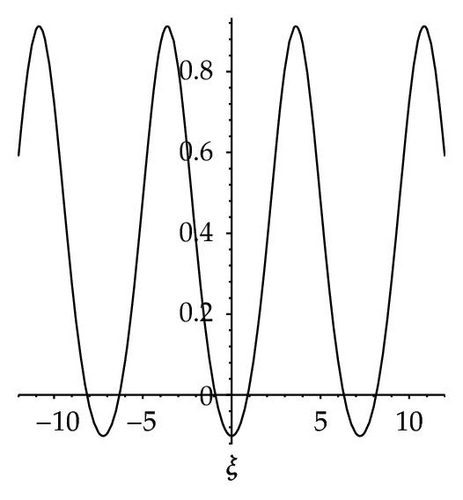
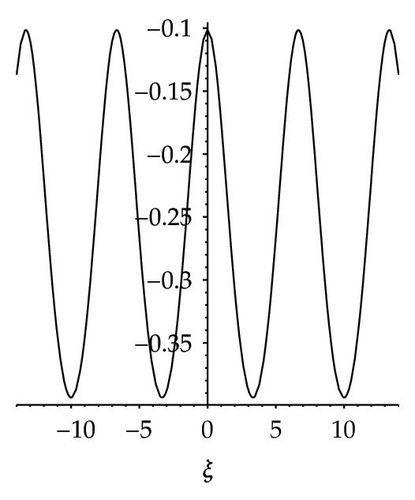
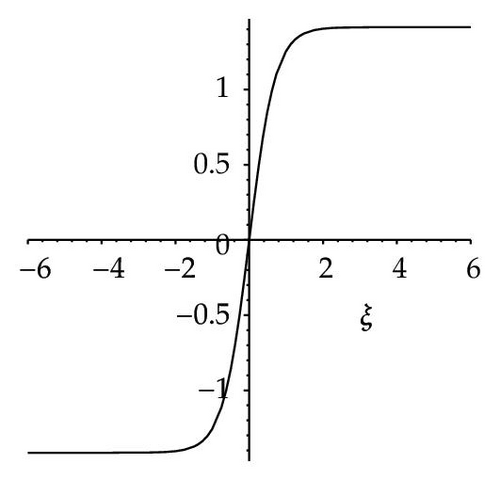
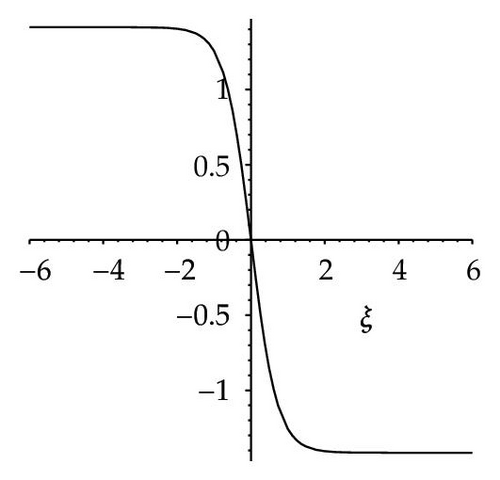
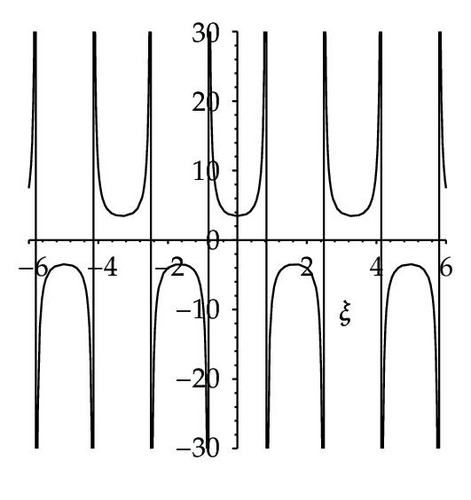
Among these aforementioned solutions, (3.59) shows a shape of solitary wave for given parameters v = 4, and σ = 1 which is shown in Figure 7(a). Equation (3.60) shows a shape of smooth periodic wave for given parameters v = 2, σ = 1, and h = 4 which is shown in Figure 7(b). Also (3.61) shows a shape of smooth periodic wave for given parameters v = 2, σ = 1, and h = 0.4 which is shown in Figure 7(c). Equation (3.63) shows two shapes of kink wave and antikink wave for given parameters v = −4, and σ = −2 which are shown in Figures 7(d)–7(e). Equation (3.68) shows a shape of singular periodic wave for given parameters v = −10, σ = −1, and h = 48 which is shown in Figure 7(f).

4. Conclusion

In this work, by using the integral bifurcation method, we study the nonlinear K(m, n) equation for all possible values of m and n. Some travelling wave solutions such as normal compactons, peculiar compacton, smooth solitary waves, smooth periodic waves, periodic blowup waves, singular periodic waves, compacton-like periodic waves, asymptotically stable waves, and kink and antikink waves are obtained. In order to show their dynamic properties intuitively, the solutions of K(n, n), K(2n − 1, n), K(3n − 2, n), K(4n − 3, n), and K(m, 1) equations are chosen to illustrate with the concrete features; using software Maple, we display their profiles by graphs; see Figures 1–7. These phenomena of traveling waves are different from those in existing literatures and they are very interesting. Although we do not know how they are relevant to the real physical or engineering problem for the moment, these interesting phenomena will attract us to study them further in the future works.

Acknowledgments

The authors thank the reviewers very much for their useful comments and helpful suggestions. This work was financially supported by the Natural Science Foundation of China (Grant no. 11161038). It was also supported by the Natural Science Foundations of Yunnan Province (Grant no. 2011FZ193) and Zhejiang Province (Grant no. Y2111160).

References

1 Rosenau P. and Hyman J. M., Compactons: solitons with finite wavelength, Physical Review Letters. (1993) 70, no. 5, 564–567, https://doi.org/10.1103/PhysRevLett.70.564, ZBL0952.35502.
10.1103/PhysRevLett.70.564
CAS PubMed Web of Science® Google Scholar
2 Rosenau P., Nonlinear dispersion and compact structures, Physical Review Letters. (1994) 73, no. 13, 1737–1741, https://doi.org/10.1103/PhysRevLett.73.1737, 1294558, ZBL0953.35501.
10.1103/PhysRevLett.73.1737
CAS PubMed Web of Science® Google Scholar
3 Rosenau P., On solitons, compactons, and lagrange maps, Physics Letters. A. (1996) 211, no. 5, 265–275, https://doi.org/10.1016/0375%2D9601(95)00933%2D7, 1377202, ZBL1059.35524.
10.1016/0375-9601(95)00933-7
CAS Web of Science® Google Scholar
4 Olver P. J. and Rosenau P., Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support, Physical Review E. (1996) 53, no. 2, 1900–1906, https://doi.org/10.1103/PhysRevE.53.1900, 1401317.
10.1103/PhysRevE.53.1900
CAS PubMed Web of Science® Google Scholar
5 Rosenau P., On nonanalytic solitary waves formed by a nonlinear dispersion, Physics Letters. A. (1997) 230, no. 5-6, 305–318, https://doi.org/10.1016/S0375%2D9601(97)00241%2D7, 1456684, ZBL1052.35511.
10.1016/S0375-9601(97)00241-7
CAS Web of Science® Google Scholar
6 Rosenau P., On a class of nonlinear dispersive-dissipative interactions, Physica D. (1998) 123, no. 1–4, 525–546, Nonlinear waves and solitons in physical systems (Los Alamos, NM, 1997)https://doi.org/10.1016/S0167%2D2789(98)00148%2D1, 1664944, ZBL0938.35172.
10.1016/S0167-2789(98)00148-1
Web of Science® Google Scholar
7 Wazwaz A. M., New solitary-wave special solutions with compact support for the nonlinear dispersive K(m, n) equations, Chaos, Solitons and Fractals. (2002) 13, no. 2, 321–330, https://doi.org/10.1016/S0960%2D0779(00)00249%2D6, 1860771, ZBL1028.35131.
10.1016/S0960-0779(00)00249-6
Web of Science® Google Scholar
8 Wazwaz A. M., Exact special solutions with solitary patterns for the nonlinear dispersive K(m, n) equations, Chaos, Solitons and Fractals. (2002) 13, no. 1, 161–170, https://doi.org/10.1016/S0960%2D0779(00)00248%2D4, 1859073, ZBL1027.35115.
10.1016/S0960-0779(00)00248-4
Web of Science® Google Scholar
9 Zhu Y. and Lü Z., New exact solitary-wave special solutions for the nonlinear dispersive K(m, n) equations, Chaos, Solitons and Fractals. (2006) 27, no. 3, 836–842, https://doi.org/10.1016/j.chaos.2005.04.057, 2166425, ZBL1088.35548.
10.1016/j.chaos.2005.04.057
Web of Science® Google Scholar
10 Domairry G., Ahangari M., and Jamshidi M., Exact and analytical solution for nonlinear dispersive K(m, p) equations using homotopy perturbation method, Physics Letters. A. (2007) 368, no. 3-4, 266–270, https://doi.org/10.1016/j.physleta.2007.04.008, 2336169, ZBL1209.65108.
10.1016/j.physleta.2007.04.008
CAS Web of Science® Google Scholar
11 Tian L. X. and Yin J. L., Shock-peakon and shock-compacton solutions for K(p, q) equation by variational iteration method, Journal of Computational and Applied Mathematics. (2007) 207, no. 1, 46–52, https://doi.org/10.1016/j.cam.2006.07.026, 2332945, ZBL1119.65099.
10.1016/j.cam.2006.07.026
Web of Science® Google Scholar
12 Wazwaz A. M., A reliable treatment of the physical structure for the nonlinear equation K(m, n), Applied Mathematics and Computation. (2005) 163, no. 3, 1081–1095, https://doi.org/10.1016/j.amc.2004.06.004, 2199467, ZBL1072.35580.
10.1016/j.amc.2004.06.004
Web of Science® Google Scholar
13 Zhu Y. and Gao X., Exact special solitary solutions with compact support for the nonlinear dispersive K(m, n) equations, Chaos, Solitons and Fractals. (2006) 27, no. 2, 487–493, https://doi.org/10.1016/j.chaos.2005.04.028, 2166403, ZBL1088.35547.
10.1016/j.chaos.2005.04.028
Web of Science® Google Scholar
14 Shang Y., New solitary wave solutions with compact support for the KdV-like K(m, n) equations with fully nonlinear dispersion, Applied Mathematics and Computation. (2006) 173, no. 2, 1124–1136, https://doi.org/10.1016/j.amc.2005.04.058, 2208001, ZBL1088.65094.
10.1016/j.amc.2005.04.058
Web of Science® Google Scholar
15 Biswas A., 1-soliton solution of the K(m, n) equation with generalized evolution and time-dependent damping and dispersion, Computers & Mathematics with Applications. (2010) 59, no. 8, 2536–2540, https://doi.org/10.1016/j.camwa.2010.01.013, 2607957, ZBL1193.35181.
10.1016/j.camwa.2010.01.013
Web of Science® Google Scholar
16 Biswas A., 1-soliton solution of the K(m, n) equation with generalized evolution, Physics Letters. A. (2008) 372, no. 25, 4601–4602, https://doi.org/10.1016/j.physleta.2008.05.002, 2424286, ZBL1221.35099.
10.1016/j.physleta.2008.05.002
CAS Web of Science® Google Scholar
17 Triki H. and Wazwaz A. M., Bright and dark soliton solutions for a K(m, n) equation with t-dependent coefficients, Physics Letters A. (2009) 373, no. 25, 2162–2165, https://doi.org/10.1016/j.physleta.2009.04.029, ZBL1229.35232.
10.1016/j.physleta.2009.04.029
CAS Web of Science® Google Scholar
18 Wazwaz A. M., General solutions with solitary patterns for the defocusing branch of the nonlinear dispersive K(m, n) equations in higher dimensional spaces, Applied Mathematics and Computation. (2002) 133, no. 2-3, 229–244, https://doi.org/10.1016/S0096%2D3003(01)00234%2DX, 1924614, ZBL1027.35118.
10.1016/S0096-3003(01)00234-X
Web of Science® Google Scholar
19 Wazwaz A. M., General compactons solutions for the focusing branch of the nonlinear dispersive K(n, n) equations in higher-dimensional spaces, Applied Mathematics and Computation. (2002) 133, no. 2-3, 213–227, https://doi.org/10.1016/S0096%2D3003(01)00233%2D8, 1924613, ZBL1027.35117.
10.1016/S0096-3003(01)00233-8
Web of Science® Google Scholar
20 Wazwaz A. M., The tanh method for a reliable treatment of the K(n, n) and the KP(n, n) equations and its variants, Applied Mathematics and Computation. (2005) 170, no. 1, 361–379, https://doi.org/10.1016/j.amc.2004.12.008, 2177229, ZBL1082.65586.
10.1016/j.amc.2004.12.008
Web of Science® Google Scholar
21 Wazwaz A. M., Compactons dispersive structures for variants of the K(n, n) and the KP equations, Chaos, Solitons and Fractals. (2002) 13, no. 5, 1053–1062, https://doi.org/10.1016/S0960%2D0779(01)00109%2D6, 1874790, ZBL0997.35083.
10.1016/S0960-0779(01)00109-6
Web of Science® Google Scholar
22 Wazwaz A. M., The tanh-coth method for new compactons and solitons solutions for the K(n, n) and the K(n + 1, n + 1) equations, Applied Mathematics and Computation. (2007) 188, no. 2, 1930–1940, https://doi.org/10.1016/j.amc.2006.11.076, 2335046, ZBL1119.65101.
10.1016/j.amc.2006.11.076
Web of Science® Google Scholar
23 Feng Z., Computations of soliton solutions and periodic solutions for the focusing branch of the nonlinear dispersive K(n, n) equations in higher-dimensional spaces, Applied Mathematics and Computation. (2006) 182, no. 1, 781–790, https://doi.org/10.1016/j.amc.2006.04.038, 2292086, ZBL1107.65088.
10.1016/j.amc.2006.04.038
Web of Science® Google Scholar
24 Abassy T. A., El Zoheiry H., and El-Tawil M. A., A numerical study of adding an artificial dissipation term for solving the nonlinear dispersive equations K(n, n), Journal of Computational and Applied Mathematics. (2009) 232, no. 2, 388–401, https://doi.org/10.1016/j.cam.2009.06.019, 2555409, ZBL1173.65053.
10.1016/j.cam.2009.06.019
Web of Science® Google Scholar
25 Deng X., Parkes E. J., and Cao J., Exact solitary and periodic-wave solutions of the K(2, 2) equation (defocusing branch), Applied Mathematics and Computation. (2010) 217, no. 4, 1566–1576, https://doi.org/10.1016/j.amc.2009.06.054, 2727399, ZBL1202.35185.
10.1016/j.amc.2009.06.054
Web of Science® Google Scholar
26 Ismail M. S. and Taha T. R., A numerical study of compactons, Mathematics and Computers in Simulation. (1998) 47, no. 6, 519–530, https://doi.org/10.1016/S0378%2D4754(98)00132%2D3, 1662379, ZBL0932.65096.
10.1016/S0378-4754(98)00132-3
Web of Science® Google Scholar
27 Ismail M. S., A finite difference method for Korteweg-de Vries like equation with nonlinear dispersion, International Journal of Computer Mathematics. (2000) 74, no. 2, 185–193, https://doi.org/10.1080/00207160008804933, 1760760, ZBL0955.65065.
10.1080/00207160008804933
Web of Science® Google Scholar
28 Ismail M. S. and Al-Solamy F. R., A numerical study of K(3, 2) equation, International Journal of Computer Mathematics. (2001) 76, no. 4, 549–560, https://doi.org/10.1080/00207160108805046, 1833773, ZBL0988.65078.
10.1080/00207160108805046
Web of Science® Google Scholar
29 Frutos J. D., Lopez Marcos M. A., and Sanz-Serna J. M., A finite difference scheme for the K(2, 2) compacton equation, Journal of Computational Physics. (1995) 120, no. 2, 248–252, https://doi.org/10.1006/jcph.1995.1161, 1349459, ZBL0840.65090.
10.1006/jcph.1995.1161
Web of Science® Google Scholar
30 Zhou J. B. and Tian L. X., Soliton solution of the osmosis K(2, 2) equation, Physics Letters. A. (2008) 372, no. 41, 6232–6234, https://doi.org/10.1016/j.physleta.2008.08.053, 2456447, ZBL1225.35194.
10.1016/j.physleta.2008.08.053
CAS Web of Science® Google Scholar
31 Xu C. H. and Tian L. X., The bifurcation and peakon for K(2, 2) equation with osmosis dispersion, Chaos, Solitons and Fractals. (2009) 40, no. 2, 893–901, https://doi.org/10.1016/j.chaos.2007.08.042, 2527834, ZBL1197.35253.
10.1016/j.chaos.2007.08.042
Web of Science® Google Scholar
32 Zhou J. B., Tian L. X., and Fan X. H., New exact travelling wave solutions for the K(2, 2) equation with osmosis dispersion, Applied Mathematics and Computation. (2010) 217, no. 4, 1355–1366, https://doi.org/10.1016/j.amc.2009.04.073, 2727373, ZBL1203.35258.
10.1016/j.amc.2009.04.073
Web of Science® Google Scholar
33 He B. and Meng Q., New exact explicit peakon and smooth periodic wave solutions of the K(3, 2) equation, Applied Mathematics and Computation. (2010) 217, no. 4, 1697–1703, https://doi.org/10.1016/j.amc.2009.10.007, 2727413, ZBL1203.35223.
10.1016/j.amc.2009.10.007
Web of Science® Google Scholar
34 Rui W., He B., Long Y., and Chen C., The integral bifurcation method and its application for solving a family of third-order dispersive PDEs, Nonlinear Analysis. Theory, Methods & Applications. (2008) 69, no. 4, 1256–1267, https://doi.org/10.1016/j.na.2007.06.027, 2426689, ZBL1144.35461.
10.1016/j.na.2007.06.027
Web of Science® Google Scholar
35 Rui W., Xie S., He B., and Long Y., Integral bifurcation method and its application for solving the modified equal width wave equation and its variants, Rostocker Mathematisches Kolloquium. (2007) no. 62, 87–106, 2352652, ZBL1148.35079.
Google Scholar
36 Rui W., Yao L., Long Y., He B., and Li Z., Integral bifurcation method combined with computer for solving a higher order wave equation of KdV type, International Journal of Computer Mathematics. (2010) 87, no. 1–3, 119–128, https://doi.org/10.1080/00207160801965321, 2598729, ZBL1182.65161.
10.1080/00207160801965321
Web of Science® Google Scholar
37 Rui W. and Lee Y. Y., Nonlinear single degree of freedom system with dynamic responses of smooth, non-smooth, and distorted travelling waves, International Journal of Nonlinear Sciences and Numerical Simulation. (2009) 10, no. 9, 1227–1235, https://doi.org/10.1515/IJNSNS.2009.10.9.1227.
10.1515/IJNSNS.2009.10.9.1227
Web of Science® Google Scholar

Citing Literature

All articles

Exact Traveling Wave Solutions of Explicit Type, Implicit Type, and Parametric Type for K(m, n) Equation

Abstract

1. Introduction

2. The Equivalent Two-Dimensional Planar System to (1.1) and Its First Integral Equations

3. Exact Solutions of Explicit Type, Implicit Type, and Parametric Type and Their Properties

3.1. Exact Solutions and Their Properties of (1.1) under h = h_O

3.2. Exact Solutions and Their Properties of (1.1) under h ≠ 0

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exact Traveling Wave Solutions of Explicit Type, Implicit Type, and Parametric Type for K(m, n) Equation

Abstract

1. Introduction

2. The Equivalent Two-Dimensional Planar System to (1.1) and Its First Integral Equations

3. Exact Solutions of Explicit Type, Implicit Type, and Parametric Type and Their Properties

3.1. Exact Solutions and Their Properties of (1.1) under h = hO

3.2. Exact Solutions and Their Properties of (1.1) under h ≠ 0

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

3.1. Exact Solutions and Their Properties of (1.1) under h = h_O