Advances in Acoustics and Vibration
Volume 2012, Issue 1 218429
Research Article
Open Access

A 3 DOF Model for an Electromagnetic Air Mount

HyungTae Kim, 

Corresponding Author

HyungTae Kim

Manufacturing System Division, KITECH, 35-3 Hongcheon, Ipjang, Chungnam, Cheonan, Republic of Korea kitech.re.kr

Search for more papers by this author
CheolHo Kim, 

CheolHo Kim

Manufacturing System Division, KITECH, 35-3 Hongcheon, Ipjang, Chungnam, Cheonan, Republic of Korea kitech.re.kr

Search for more papers by this author
SungBok Kang, 

SungBok Kang

Manufacturing System Division, KITECH, 35-3 Hongcheon, Ipjang, Chungnam, Cheonan, Republic of Korea kitech.re.kr

Search for more papers by this author
KangWon Lee, 

KangWon Lee

Manufacturing System Division, KITECH, 35-3 Hongcheon, Ipjang, Chungnam, Cheonan, Republic of Korea kitech.re.kr

Search for more papers by this author
JaeHo Baek, 

JaeHo Baek

RMS Technology, Techpia Building, 774 Dujeonng, Seobuk,Chungnam, Cheonan, Republic of Korea rmsmotion.com

Search for more papers by this author
HyunHee Han, 

HyunHee Han

Manufacturing System Division, KITECH, 35-3 Hongcheon, Ipjang, Chungnam, Cheonan, Republic of Korea kitech.re.kr

Search for more papers by this author
First published: 18 January 2012
https://doi.org/10.1155/2012/218429
Citations: 5
Academic Editor: Luc Gaudiller

Abstract

A 4 × 4 matrix model with three degrees of freedom is proposed as a means for controlling microvibrations and applied to an electromagnetic isolator. The model was derived from an assumption based on small- and low-frequency vibrations. The coordinates of the 3 DOF was composed of the 4 variables, representing a vertical position, pitch, roll, and a proof term. The coordinates were calculated from the 4 position sensors in the isolator and formulated into a 4 × 4 matrix, which possesses inversive full rank. The electro-magnetic isolator was built for a simulated machine in semiconductor manufacturing and consisted of a heavy surface plate, sensors, amps, a controller, and air springs with electromagnets. The electromagnets are installed in a pneumatic chamber of the individual air spring. The performance of the 3 DOF model was experimented and compared with that of a 1 DOF model in an impact test. The settling time in the result was reduced to 25%.

1. Introduction

Vibration is one of the important factors in semiconductor manufacturing, affecting the processes related to laser optics. Vibration is unpredictable, irregular, and generated by various sources. Studies have been conducted to isolate vibrational effects from the environment. Air spring is one of the solutions and has been used widely in industrial field. Sensitive machines, such as lithography, are placed on air springs in order to isolate vibration. An air spring accumulates air pressure in a chamber and floats a heavy load on a surface plate. This kind of isolator is usually called an air mount. An air mount supports tons of heavy weight under a manufacturing machine. The number of the air springs is determined by the weight which the air mount will support. The weight can be several tons including a surface plate and a manufacturing machine. The physical combination of the heavy load and the springs usually causes resonance at low-frequency vibrations. This causes long oscillation due to vibrational disturbances, producing problems in the manufacturing process. When a high-speed machine immediately stops at an instance, several seconds are required to regulate the vibration in the resonance frequency.

Active controls, such as pneumatic, electromagnetic (EM), and magnetorheological (MR) methods, are coupled with the air springs in an air mount. A pneumatic control is a commonly employed method for active control. Air pressure in the air chambers is controlled by adjusting air valves [1–3]. Although other active controls are applied in the air mount, the pneumatic control is essential because EM and MR cannot generate power as high as pneumatics. The pneumatics is in charge of large vibrations, the MR manages small vibrations, and EM controls micro-scale vibration. MR fluid can be used to reduce the oscillation in an air mount [4]. When vibration occurs in the mount, a damping force will increase and reduce oscillation due to the viscosity of the MR fluid. Piezoelectric (PZT) actuators can be applied to the air mount [5]. The PZT actuator is coupled with an air spring through a serial connection. EM actuators are another method to reduce the resonance [6]. The vibration in an air spring is varied by the EM force.

An air mount usually has multiple actuators, vibration occurs in a six DOF space, and a multi-DOF model is reported in many cases [7–9]. A common method isolating an air mount is controlling the air flow. Time delay control [10], predictive control [11], and conventional PID control [12] adjust the pneumatic status in order to isolate vibration.

Although EM may be applied as a means for controlling vibrations [13–16], the load capacity is not enough to sustain tons of mass; thus, it cannot be used in the manufacturing system. Microvibration can be managed by combining EM and pneumatic forces. Most of this air mount regulates vibration energy by vertical motion, so a rigid surface plate shows vertical, pitch, and roll motions. Planar and rotational motion is negligible for cases in which moving mass is excluded. A 3 DOF model of the air mount with these vertical, pitch, and roll motions; these can be considered under the assumption that microvibration occurs. However, a 3 DOF model in an air mount has 3 coordinate variables and four isolating devices. Thus, difficulty arises when finding the inverse matrix for the control algorithm. This study proposes a 3 DOF model for microvibration in typical isolators using 4 isolating devices. The model includes a control algorithm and contains an inversible matrix in the coordinate conversion. The proposed model was applied to an air mount which provided 4 EM air springs. The experiment was carried out for a single DOF and 3 DOF model.

2. Full-Rank 3 DOF Model

An air mount supported four air springs under a surface plate. The surface plate was assumed to be a rigid body exhibiting no deformation. Vertical, pitch, and roll motions of a surface plate can be derived from the motion of the four air springs. Noncontact sensors measured the displacements of individual air springs. The surface plate was heavy and large, making the vertical displacements of the air springs relatively small. Planar and rotational motion was not considered excluding moving mass. Motion of the air mount can be described by the variables in Figure 1. Vertical displacement of individual actuators is zn and that of center in the surface plate is z. The displacement of z can be calculated by averaging the vertical displacements of all of the actuators, as shown in
()
The planar distance between the center and the actuators is designated as d1 and d2. The roll and pitch angles are ϕ and θ, respectively. ϕ and θ can be derived from the zn, as shown in Figure 2. Equation (2) is the relative distance between z and z1:
()
The motions of other points can be written similarly, as given by the following equations:
()
The equation can be arranged for ϕ and θ without z:
()
ϕ and θ can be assumed as infinitesimal because d1 and d2 are relatively larger than zn. The d1 and d2 are 1000–3000 mm for the manufacturing machines, and zn is under hundreds of micron in common state and 3 mm in exceptional state. The angle due to the motion is approximately under 0.2 degree. If infinitesimal motion is assumed, sin ϕ and sin θ are approximated as ϕ and θ:
()
An additional coordinate, the proof term, ε, can be defined as follows:
()
The ε is the difference of diagonal pairs in the mount and should theoretically be zero. But the value of ε can be a small constant because of sensor noise and geometrical error. Therefore, ε can be used as an index for modelling errors. From (2) through (6), a full-rank matrix form can be derived as follows:
()
This matrix converts the actuator coordinate to that of the surface plate. d1 and d2 are positive, and the matrix is always inversible. The matrix can be symbolized as T for coordinate conversion:
()
T−1 is calculated as follows:
()
Differentiation of the coordinate can be obtained from
()
Differentiation is applied to (3)–(6) under the condition that cos ϕ ≈ 1, cos θ ≈ 1 for infinitesimal motion. Then, can be defined as follows:
()
Double differentiation can be formulated with
()
The following equation can be derived from infinitesimal motion, , and . Thus, the following relation can be obtained:
()
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Variables in an air mount.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Coordinate conversion in an air mount.

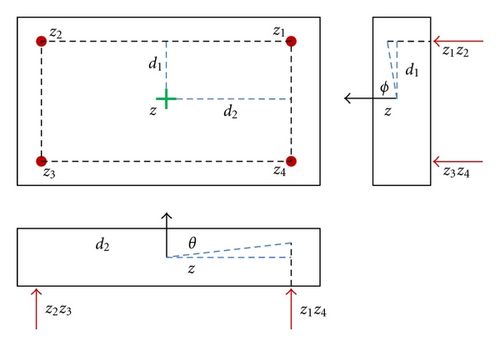
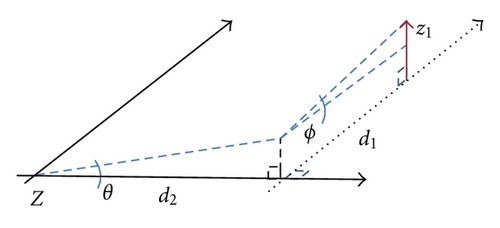
3. Control Method

An EM air spring is composed of EM parts, the pneumatics and attach assemblies. The pneumatics, which possesses damping and elastic characteristics, supports the heavy load. The characteristics are linear and in the microvibration range. The EM component generates the control force F, which reduces vibration. A disturbance force is exerted from the environment:
()
The EM force is governed by the electric current and the size of the gap between a coil and a magnet. If the gap is large enough to be placed in the linear range of the current under an assumption of microvibration, then the force is function of the current, F(I). The electric current is formed by voltage level V which is determined from control input and sensor outputs in a controller:
()
The V is determined by the error between the reference level and the measured level:
()
The P control is applied to the pneumatics using the feedback from mechanical levelers. A PD feedback control method is applied to the EM components with a noncontact displacement sensor. The 1 DOF model is defined by individual actuators that control the reference positions. The motion of the surface plate is defined as G(s), feedback is H(s), error is E(s), and the controller is K. When vibration occurs, a sensor in each actuator measures the vibration from a reference level and a controller determines the output of the actuator. The loop is formed for each sensor and actuator. The control loop is easy and simple to build and effective for uniaxial vertical vibration. However, the 1 DOF model is weak at accounting for multiaxial vibration because each actuator controls its own vibration without assisting other actuators.
The 3 DOF model attempts to control the vibration within a view of a surface plate. The control output of each actuator is determined in consideration of other sensors, so it can be better at managing multiaxial vibration. The 3 DOF model’s control loop can be constructed with the coordinate conversion. The air mount system has an actuator coordinate, so the conversion matrix to 3 DOF motion is necessary to form the feedback loop, as shown in Figure 3. The transfer function of the system can be summarized as follows:
()
1 DOF model forms a PD feedback loop and controls the vibration in individual measuring point. An EM spring is activated using its corresponding sensor, but the action is not coupled with other sensors. So, the 1 DOF model is actually SISO. However, the 3 DOF model is coupled with other sensors and generates multiple DOF motion, so the 3 DOF model is MIMO.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Control loop of the 3 DOF model for an air mount.

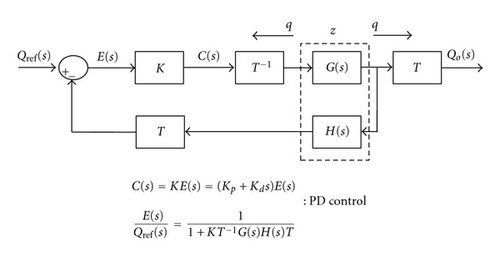
4. Experiment

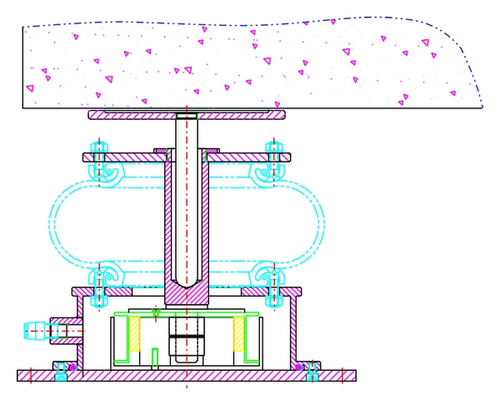
Figure 4 shows the air mount that was constructed for the experiment. The weight of the surface plate was 3.0 ton, and its size was 2000 mm × 2000 mm. Sensors and actuators were installed on each corner of the surface plate. Displacement due to vibration in common operating conditions of air mount is within hundreds of microns and ±3 mm in exceptional situation. The range of infinitesimal vibration was within ±50 μm. The internal structure of an EM air spring is shown in Figure 5. A magnet and a coil were installed in the air chamber. The magnet was fixed on the base, and a coil was attached under an upper plate. The upper plate was floated by compressed air, allowing relative motion between the magnet and the coil.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
An air mount with EM actuators.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Cross section of an EM air spring.

The impact point was a corner in the air mount, giving a 3 DOF vibration. A PC-based embedded system (NI PXI-8108) was used as a controller. The vibration was measured by gap sensors (Santec LS-500) with the accuracy of 3 um. An A/D board (NI PXI-6250) received the analog output of sensors. The control program was built by C++ and control period was 10 ms. The controller output was transferred to a 4-channel linear AMP via a D/A board (NI PXI-6733). The maximum power of the linear AMP was 250 W for each channel. The sensor output was also measured with an oscilloscope (Tek 2024B).

The test was conducted using the pneumatic control and not using the pneumatic control. EM force was not sufficiently large enough to recover the heavy weight, and air leakage was unavoidable in the air mount—thus, actual situations require a pneumatic control. However, if operating time is short, then the leak is negligible. The effect of the EM control can be easily monitored in the case in which a pneumatic control is not used. The PD gain for the 1 DOF model was 1.9 and 0.7. The PD gain for the 3 DOF model was 1.6/0.2, 1.3/0.2, 1.3/0.2, and 15.0/3.0 for (z, ϕ, θ, ε). An impact was acted on a corner of the surface plate to generate 3 DOF vibration and check the control performance.

The ε was monitored with a passive control using an impact applied at the center of the surface plate. Four triaxial accelerometers (PCB 3713D1FD3G) were used to measure acceleration. A high-speed A/D converter measured the signal of acceleration; a TMS-C6713-based DSP was used (DSignT C6713).

5. Results

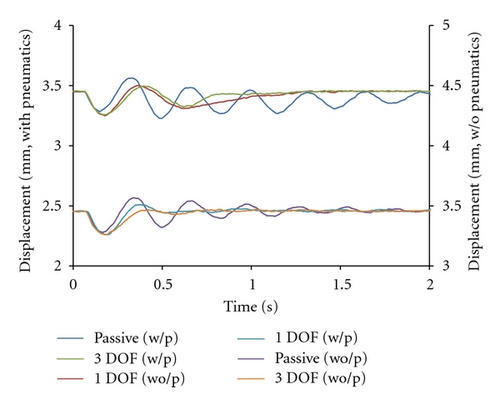
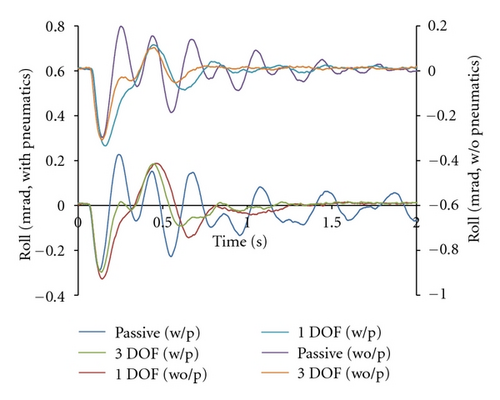
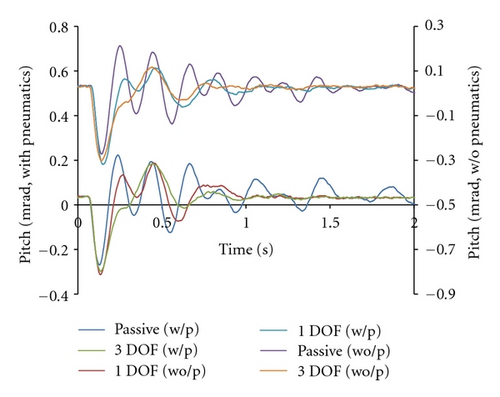
The control response of the 3 DOF model is shown in Figures 6–8. The horizontal axis represents time, and the vertical axis is displacement in Figure 6, roll in Figure 7, and pitch in Figure 8. The response of 6 experimental conditions is plotted in each figure. The conditions are passive control, 1 DOF EM control, and 3 DOF EM control with and without pneumatic control. Passive control signifies the state in which the pneumatic control was employed without an EM control. The settling time without the pneumatic control is faster than that with a pneumatic control. The pneumatic control allows air to leak in the mount and has a longer settling time to compensate the leakage. However, small amounts of air escape from the air mount, thus the mount can be used in short periods of time without a pneumatic control. Passive control takes the most amount of time to reach steady state. Roll motion is similar to pitch motion because the top shape of the surface plate is square. The settling time of 1 and 3 DOF with a pneumatic control was 0.6 sec. The settling time of 1 and 3 DOF without the pneumatic control was 1.2 and 0.9 sec, respectively. The response of the 3 DOF model was 25% faster than that of the 1 DOF model. Oscillation in the cases with an EM control is regulated faster than in those without an EM control. Exponential decay is shown in the plot due to slower response of a pneumatic control. An EM control was effective in the oscillation, and a pneumatic control is useful to reduce steady-state errors.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Motion of z-axis in an air mount.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Motion of ϕ-axis in an air mount.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Motion of θ-axis in an air mount.

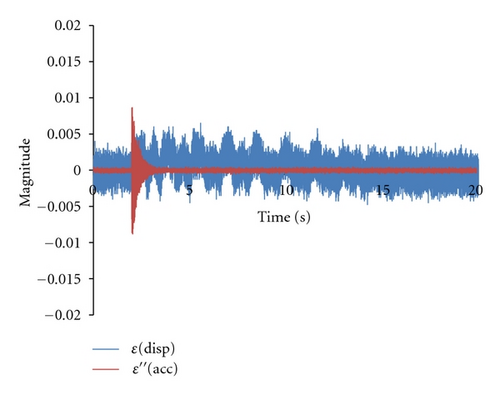
The response of ε is shown in Figure 9. The horizontal axis represents time, and the vertical axis is the magnitude of displacement and acceleration. Both of the responses fluctuated after impact and converged to zero in steady state. The level of the responses was small in value and was approximated in the noise level. A transient acceleration response occurred at the moment of impact. The transient response was 428 Hz and was considered to be a solid vibration of the surface plate due to the impact. Therefore, the transient response was not related to the motion of the surface plate and the proposed model is correct. The magnitude of ε was in noise level in the experiments.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Acceleration response of ε.

6. Conclusion

This study proposed a 3 DOF control method for an air mount that reduces microvibration and resonance in semiconductor manufacturing. The air mount was composed of a heavy weight and active air springs. The heavy weight was supported by 4 active air springs. The active air spring consisted of pneumatic and EM components. The EM components generated an EM force that reduced oscillation. The 3 DOF model was derived from the geometric conditions under an assumption of microvibration. The logic contained a 4 by 4 matrix which was full rank and inversible. The control signal of the EM components was determined by the 3 DOF model from a gap sensor. The 3 DOF model was experimentally applied to an air mount. The proposed model effectively controlled microvibration.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.