Volume 2012, Issue 1 205686

Research Article

Open Access

A Positivity-Preserving Numerical Scheme for Nonlinear Option Pricing Models

Shengwu Zhou,

Shengwu Zhou

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Wei Li,

Corresponding Author

Wei Li

[email protected]

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Yu Wei,

Yu Wei

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Cui Wen,

Cui Wen

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Shengwu Zhou,

Shengwu Zhou

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Wei Li,

Corresponding Author

Wei Li

[email protected]

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Yu Wei,

Yu Wei

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

Cui Wen,

Cui Wen

College of Sciences, China University of Mining and Technology, Jiangsu, Xuzhou 221116, China cumt.edu.cn

Search for more papers by this author

First published: 17 December 2012

https://doi.org/10.1155/2012/205686

Citations: 3

Academic Editor: Mohamad Alwash

Share a link

Email
Wechat
Bluesky

Abstract

A positivity-preserving numerical method for nonlinear Black-Scholes models is developed in this paper. The numerical method is based on a nonstandard approximation of the second partial derivative. The scheme is not only unconditionally stable and positive, but also allows us to solve the discrete equation explicitly. Monotone properties are studied in order to avoid unwanted oscillations of the numerical solution. The numerical results for European put option and European butterfly spread are compared to the standard finite difference scheme. It turns out that the proposed scheme is efficient and reliable.

1. Introduction

It is widely recognized that the value of a European option can be obtained by solving the linear Black-Scholes equation under quite restrictive assumptions (such as liquid, frictionless, and complete markets) [1, 2]. However, these restrictive assumptions are never fulfiled in reality. In order to conform the actual situation, many modified Black-Scholes models have been proposed in recent years, such as transaction costs (Leland [3], Palmer [4], Hoggard et al. [5], Barles and Soner [6], and Jandačka and Ševčovič [7]), illiquid market (Frey and Patie [8], Sircar and Papanicolaou [9], Liu and Yong [10], etc.), and volatility uncertainty (Avellaneda et al. [11]). These models result in quasilinear or fully nonlinear Black-Scholes equations.

In this paper, we are interested in the option pricing model with transaction costs proposed by Barles and Soner [6] that are motivated by Hodges and Neuberger [12]. In their model, the value V(S, t) of the option satisfies the following partial differential equation:

()

with the nonlinear volatility σ(V_SS) that reads

()

and the terminal condition

()

where S is the price of the underlying asset, T is the maturity date, r is the risk-free interest rate, σ₀ is the asset volatility, and

, with the proportional transaction cost μ, the risk aversion factor γ, and the number N of options to be sold. Ψ(x) is the solution of the following ordinary differential equation:

()

The existence and uniqueness of the solution of (1.1)–(1.3) have been shown by the theory of stochastic optimal control in [6]. However, analytical solutions cannot be found because of fully nonlinear properties of (1.1); thus, we need to compute the option values numerically.

There have been rich achievements for the numerical method of linear Black-Scholes equations (e.g., see [13–17]). As for the nonlinear situation, only a few results can be found. There is a stable numerical scheme developed in [7] (see also [18] for application to a general class of nonlinear Black-Scholes equations) for the so-called gamma equation (a quasilinear parabolic equation for the SV_SS). Recently Kútik and Mikula [19] did some progress in showing its stability and accuracy for nonlinear Black-Scholes equation. Company et al. [20–22] construct explicit finite difference schemes for (1.1)–(1.3), and consistency and stability are studied. However, they have the disadvantage that strictly restrictive conditions on the discretization parameters are needed to guarantee stability and positivity. The implicit schemes do not have this disadvantage, but they are quite time-consuming. Yousuf et al. [23] develop a new second-order exponential time differencing (ETD) scheme to avoid unwanted oscillations near the non-smooth nodes for the Hoggard-Whalley-Wilmott (HWW) model [5] based on the Cox and Matthews approach [24] and partial fraction version of the matrix exponential, but the theoretical analysis of stability and convergence are not studied. Some authors (for instance, Düring et al. [25] for European options, Dremkova and Ehrhardt [26] for American options) construct high-order compact difference schemes with frozen values of the nonlinear coefficient of the nonlinear Black-Scholes equation to make the scheme linear and show that the resulted linearized problem is stable.

On the other hand, since the value of option is nonnegative, it is very important to make numerical schemes preserve the positivity of solution. Several authors have developed some schemes that guarantee the positivity of solutions for ordinary differential equations [27, 28] and parabolic equations [29]. In [30], Chen-Charpentier and Kojouharov propose an unconditionally positivity-preserving scheme for linear advection-diffusion reaction equations. They construct a nontraditional discretization of the advection and diffusion terms by the approximation of the spatial derivatives using values at different time levels. Motivated by this work, we will develop the method to a nonlinear Black-Scholes equation, and some properties (such as stability, monotonicity, and consistency,) of numerical scheme are studied in this paper. The new numerical method unconditionally preserves the positivity of the solutions, the stability, and monotonicity of the scheme. In addition, the designed numerical approximations allow us to solve the discrete equation explicitly, which reduces the time of calculation and increases the efficiency of the methods.

The rest of the paper is organized as follows. In the next section the original problem (1.1)–(1.3) is transformed into a nonlinear diffusion problem by an appropriate change of variables and some properties of the function Ψ(x) are given. In Section 3, the discretization method is constructed. In Section 4, we prove the boundedness of coefficients, positivity, and monotonicity of the numerical scheme. Stability and consistency are studied in Section 5. In Section 6, numerical experiments for European put option and a European butterfly spread are presented to support these theoretical results. Finally, some conclusions are drawn in Section 7.

2. The Transformed Problem

For the convenience in the numerical processing and the study of the numerical analysis, we are going to transform the problem (1.1)–(1.3) into a nonlinear diffusion equation. Taking the variable transformation

()

the original problem (1.1)–(1.3) is transformed into

()

with the initial condition

()

and the boundary condition

()

The following two lemmas give the properties of the function Ψ appearing in (1.2), which will play an important role in the numerical analysis and numerical calculation.

Lemma 2.1 (see [20].)The solution Ψ of ordinary differential equation (1.4) exists and is unique, and it satisfies,

(i)
Ψ is an increasing function mapping the real line onto the interval (−1, +∞).
(ii)
Ψ = Ψ(A) is implicitly defined by
()
(iii)
if A > 0, then the function Ψ(A) is bounded and satisfies
()

where

()

Lemma 2.2 (see [20].)Let g(A) = AΨ(A), then g(A) is continuously differentiable at A = 0 and satisfies

()

where A₂ and d₂ are given by (2.7), and

()

3. The Unconditionally Positivity-Preserving Scheme

Since the value of an option is nonnegative, it is important that numerical scheme is positivity preserving.

We see that the problem (2.2) is described in an infinite domain ℝ⁺ × [0, T], which makes it difficult to construct scheme effectively. Let us consider the truncated numerical domain Ω = [0, B]×[0, T] and discretize it in the following form. We introduce a grid of mesh points (x, τ) = (x_i, τ_n), where x_i = ih, τ_n = nk, i = 0,1, …, N, n = 0,1, …, L, and the spatial step size given by h = B/N, and the time step size is k = T/L. Let us denote the approximation of u(x_i, τ_n) by

and define the following finite difference approximations of derivatives:

()

Clearly, the approximation used to calculate the second partial derivative of u with respect to x is nonstandard. From (2.2), we can obtain the positivity-preserving finite-difference numerical scheme as follows:

()

Scheme (3.2) is equivalent to

()

where

()

Remark 3.1. From property (i) of Lemma 2.1, Ψ takes values in the interval (−1, +∞), so the coefficients are nonnegative, that is, for any i, n.

Obviously, numerical scheme (3.3) is unconditionally positive for a nonnegative payoff . However, we cannot obtain the numerical solution explicitly since the nonlinear term involves the value u at the time level n + 1, which makes it quite difficult to prove the stability of the scheme presented previously. In fact, the numerical scheme (3.3) can only be solved by a nonlinear iteration in each time step which is quite time-consuming.

In order to obtain an efficient scheme, we correct the approximation of the nonlinear coefficients in (2.2) by using the standard second-order central difference. Thus the corrected numerical scheme is as follows:

()

where

()

Since the calculation of (3.5) for i = 0 and i = N requires us to know the fictitious values and , we obtain them using the linear extrapolation as follows:

()

Thus the values of boundary points turn out

()

The left boundary condition is not needed and in fact must not be prescribed in the case of a parabolic equation with degenerating diffusion term at x = 0. This is known in the literature as the Fichera condition [31] (see [18] for application in Black-Scholes equations, Chapter 8, (8.25)). The Fichera condition is just a comparison of the speed of degeneration versus. speed of advection at the boundary x = 0. Fortunately, the left boundary condition in (3.8) is a consequence of (3.5) with . The only boundary condition that can be prescribed is the right boundary condition at x = B. For the convenience in the numerical calculation, let us denote the vectors , then numerical scheme (3.5), (3.8) can be written in matrix form

()

where

()

In order to study the related properties of numerical scheme (such as monotonicity and stability), we need to know the behaviour of appearing in the nonlinear team .

Lemma 3.2. With the previous notation, appearing in the nonlinear team satisfies the scheme

()

Proof. From (3.6) and (3.7) we can know for i = 0 and i = N that

()

Putting (3.5) into the expression (3.6) of , and after a simple calculation we can obtain (3.12).

On the other hand, the most common option price sensitivities are the first and second derivatives with respect to the price of the underlying asset, that is, “delta” and “gamma”, respectively. These are important features in risk management and are challenging to compute numerically. From the transformation (2.1) we can obtain the approximations of Greeks of the option as follows:

()

4. Properties of the Numerical Scheme

4.1. Boundedness of the Coefficients

For the sake of convenience, we introduce the following definition.

Definition 4.1 (see [32].)If x = [x₁, x₂, …, x_N] is a vector in ℝ^N, then its 1-norm is denoted by , and maximum-norm is denoted by ∥x∥_∞ = max_1≤i≤N | x_i|.

The following theorem shows that the nonlinear team appearing in (3.5) is bounded.

Theorem 4.2. Let , then the following properties hold true.

(i)
∥Δⁿ∥₁ is nonincreasing.
(ii)
The nonlinear team appearing in (3.5) satisfies
()

where

()

with A₂, d₂, and Ψ′(A₂) given by (2.7).

Proof. Property (i) is proved using the induction principle over index n.

For n = 0, from Lemma 3.2 and by Remark 4.7, it follows that

()

Taking into account (3.13) and (4.3), we have

()

Thus property (i) is proved for n = 0.

Now, let us assume that property (i) holds true up n, that is,

()

For 1 ≤ i ≤ N − 1, from Lemma 3.2, it follows that

()

Taking into account

, we have

()

Hence property (i) is proved completely.

On the other hand, from (3.6) and the monotonic increasing property of Ψ (see Lemma 2.1), it follows that

()

Since x_i ∈ [0, B] and from the property (iii) and property (i) of Lemma 2.2, we have

()

Thus the proof of theorem is complete.

4.2. Positivity

Since the value of option is nonnegative, a nice property of the numerical scheme for the pricing equation is positivity-preserving.

Clearly, all the coefficients of the numerical scheme (3.5) are nonnegative (see Theorem 4.2). Hence, for a nonnegative payoff , the following result has been established.

Proposition 4.3. The numerical scheme (3.5), (3.8) is unconditionally positive.

Remark 4.4. is also unconditionally positive, that is, if for 0 ≤ i ≤ N, then for 0 ≤ i ≤ N, 0 ≤ n ≤ L.

4.3. Monotonicity

For the sake of convenience in the presentation, we introduce the following definition of a monotonicity preserving numerical scheme.

Definition 4.5 (see [31].)In numerical scheme , we say that it is monotonicity-preserving. If each time that or for all i, then it occurs that or for all i.

The next result shows the monotonicity of the numerical scheme.

Theorem 4.6. The numerical scheme (3.5), (3.8) is unconditionally monotonicity-preserving with 0 ≤ i ≤ N, 0 ≤ n ≤ L.

Proof. Let us write

()

Assuming that

for 0 ≤ i ≤ N − 1, 0 ≤ n ≤ L − 1, then from (3.5), it follows that

()

that substituting i by i + 1 one gets

()

From (4.10), (4.11), and (4.13), it follows that

()

Taking into account (4.1) and (4.14) for i and i + 1, we have

()

The monotonicity of the scheme in the internal mesh points has been proved.

In an analogous way, we can verify that

()

Similarly, we can prove that if , then for 0 ≤ i ≤ N − 1, 0 ≤ n ≤ L − 1.

Thus the proof of theorem is complete.

Remark 4.7. If the payoff f(x) is nondecreasing with f(0) = 0 (e.g., f(x) = max{x − K, 0}), then for a fixed n with 0 ≤ n ≤ L.

5. Stability and Consistency

5.1. Stability

Theorem 5.1. The difference scheme (3.5), (3.8) is unconditionally ∥·∥_∞-stable.

Proof. From (3.5), let us write

()

Since all the coefficients of (5.1) are nonnegative, then using triangle inequality, it follows that

()

so that

()

According to the definition of the maximum norm, it follows that

()

Thus the result is established.

5.2. Consistency

The proposed new difference scheme (3.5) is explicit, unconditionally positive, and unconditionally stable; however, it is not unconditionally consistent. There are extra truncation error terms since the approximations to second derivatives with respect to x are at different time levels.

The following theorem gives the consistency condition of the difference scheme (3.5).

Theorem 5.2. With the previous notation, suppose that the exact solution u of (1.1)–(1.3) satisfies . Then the local truncation error is given by

()

Proof. Let us write the scheme (3.5) in the form

()

Using Taylor′s expansion about (x_i, τ_n) and

, it follows that

()

where

()

From (5.5)–(5.8), it follows that the local truncation error takes the form

()

Let us introduce the notation

()

Using function g(A) introduced in Lemma 2.2, it follows that

()

From Lemma 2.2, (5.11), and

, it is easy to know that

()

Thus the result has been proved.

From Theorem 5.2, we can see that the meshes should satisfy k/h² → 0 as k and h go to zero in order to ensure the consistency. Therefore, the key to the convergence of the scheme is the consistency rather than the stability. In actual calculation, we can choose the time step depending on the spatial size so that inconsistent terms go to zero.

6. Numerical Experiments

In this section, we implement the positivity-preserving scheme (3.5), (3.8) on European put option and European butterfly spread. We analyse the effectiveness of the method and compare it with the numerical scheme (SFD1) given in [20] and a standard forward Euler finite difference scheme (SFD2)

()

which is analysed in [21]. The function Ψ is calculated with (2.5) using the “fsolve” function in Matlab. Both the experiments are performed for large values of σ₀ to visualize the sensitivity of the methods towards high volatility.

6.1. European Put Option

A European put option is a contract where the owner of the option has the right to sell an underlying asset S(t) for a fixed amount, known as the strike price K, at the expiry date T. The payoff function f(S) is given by

()

We choose the parameters as

()

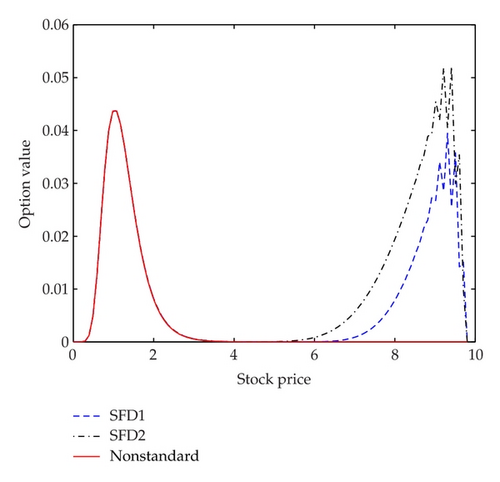
Equations (1.1)–(1.3) give analytical solution for only a = 0 (see [6]). Figure 1 (the left one: a = 0, the right one: a = 0.02) gives the option value using scheme (3.5) and schemes (SFD1 and SFD2) in [20, 21], which shows that our scheme stable, monotonous, and is able to produce solution that is close to the exact solution, but numerical solution of scheme (6.1) appears as spurious oscillation for k = 0.0005 and h = 0.1.

Details are in the caption following the image — **Figure 1 (a) a = 0**
Open in figure viewer PowerPoint

The values of European put option under different schemes with the computational parameters h = 0.1 and k = 0.0005.

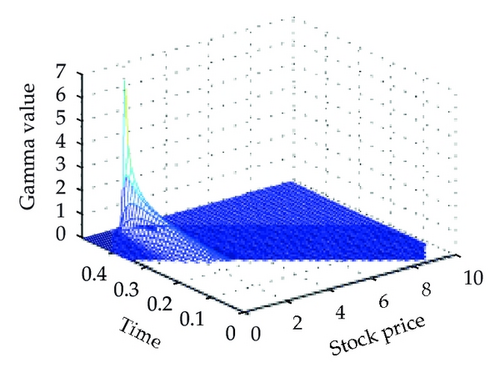
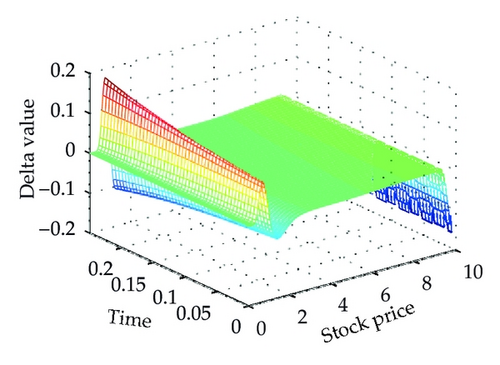
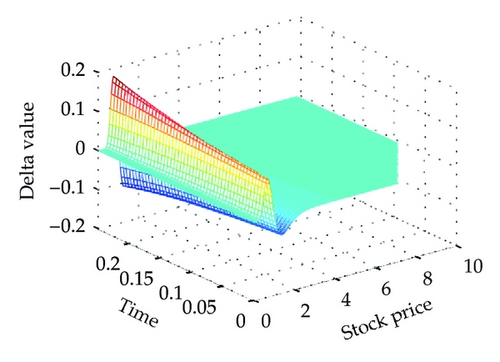
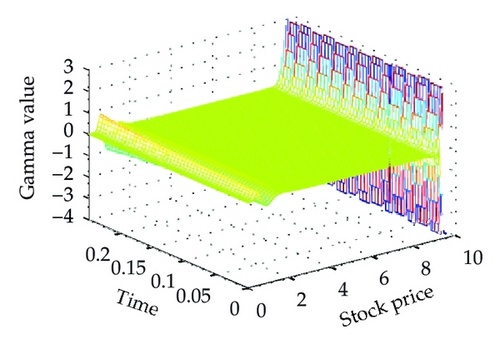
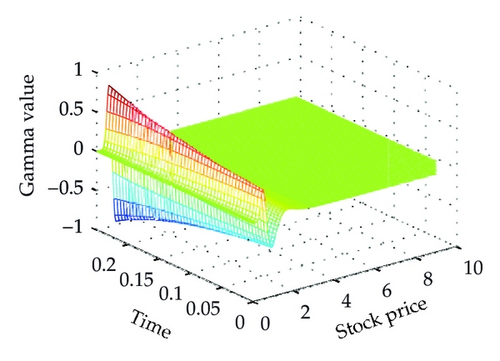
Moreover, Figure 2 presents the related hedging parameters of European put option using the two schemes. We can see that our proposed scheme produces smoother solutions than standard scheme for the delta and gamma. In addition, the gamma is positivity preserving and is maximal as it closes the strike price K = 2.

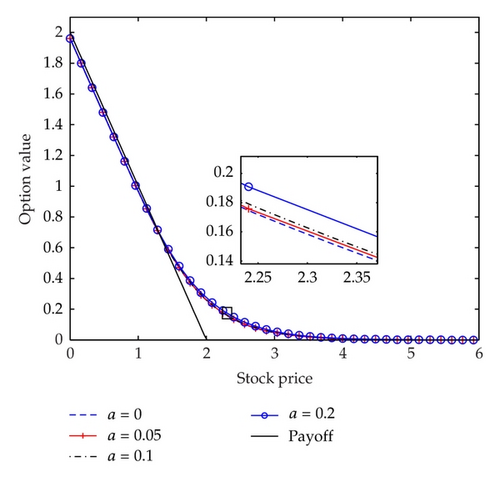
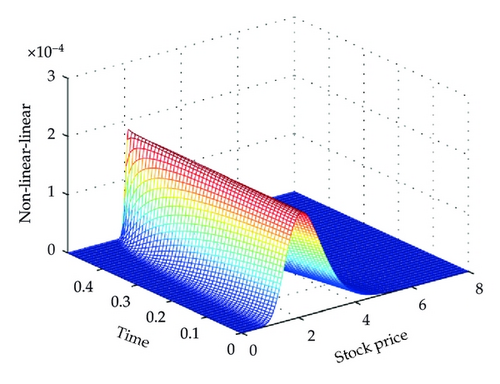
Next we consider the influence of transaction costs (parameter a) on the value of European put option (Figure 3). The left one shows the change of the option value with the parameter a, and the right one presents an evolution profile of the difference V_nonlinear(S, t) − V_linear(S, t) between our proposed scheme with transaction costs and without transaction costs. We can see that the difference is not symmetric, but decreases towards the expiry date, and is maximal close to the strike price K = 2, where the nonlinear value is significantly higher than the linear value.

6.2. European Butterfly Spread

A butterfly spread is a combination of three-call options with three-strike prices, in which one contract is purchased with two outside strike prices and two contracts are sold at the middle strike price. The payoff function f(S) is given by

()

where K₁, K₂, and K₃ are the strike prices that satisfy K₁ < K₂ < K₃ and K₂ = (K₁ + K₃)/2.

We choose the following parameters:

()

the time step k = 0.000455, and the spatial step h = 0.1.

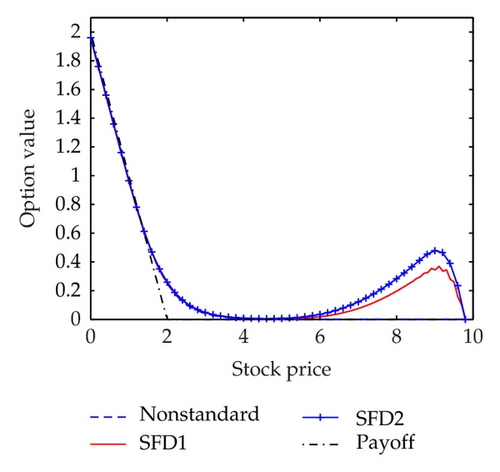
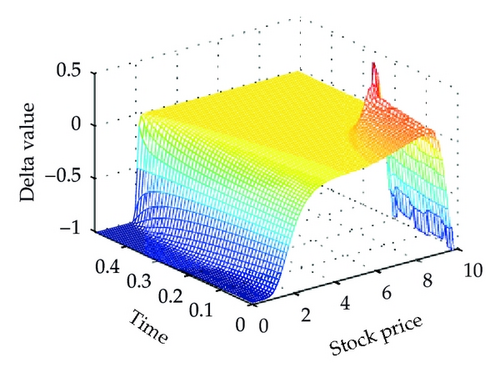
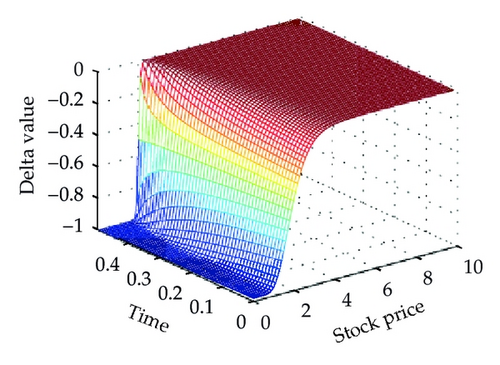
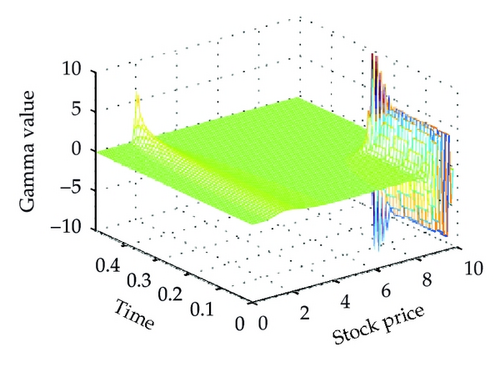
Figure 4 shows the different solutions of two schemes at t = 0 for a = 0.02. We can see that our proposed scheme is smooth and stable at the same step sizes. Moreover, Figure 5 shows the Greeks of the numerical solution calculated with scheme (3.14), which is different from the vanilla option. The standard scheme (the left one) is unstable and produces unwanted oscillations which are not present while using our proposed scheme (the right one).

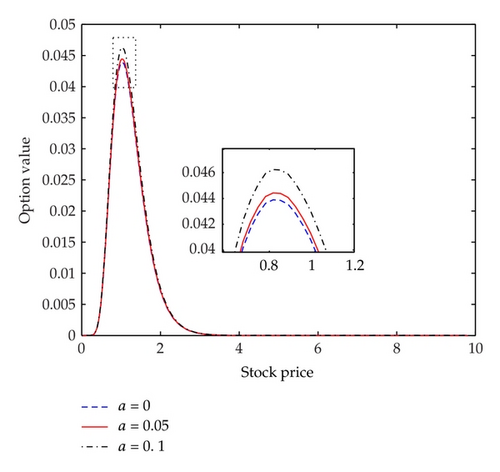
The last two figures show the value of European butterfly spread with different transaction costs (parameter a). It is evident from Figure 6 that butterfly spread becomes more expensive in the presence of transaction cost and the difference is maximal as it closes the strike price K₂ = 1, which is similar with the vanilla option.

7. Discussions and Conclusions

In this paper, we have extended the numerical method in [30] to nonlinear situation and presented the numerical scheme for a nonlinear Black-Scholes equation in the presence of transaction costs. The numerical method is based on a nonstandard approximation of the second partial derivative ∂²u(x_i, τ_n)/∂x² by

, and the nonlinear team is treated explicitly, which guarantees to solve the original problem without iteration. The scheme is unconditionally positive and stable, but it is conditionally consistent. In fact, as

, the scheme effectively solves the nonlinear parabolic equation

()

where

()

It means that the new scheme converges to a solution of (2.2) if k/h² → 0. Otherwise, (if k/h² is fixed) it converges to a solution of (2.2) in a different time scale. In fact, it can be seen from Theorem 5.2, where the truncation error really depends on the ratio k/h², which is also the reason that we consider the smaller ratio k/h² in the experiment. The numerical results show that our method produces better numerical solutions than the schemes in [20, 21] with the same step sizes. In the future work, we will extend the method to the problem of American option pricing.

Acknowledgments

The authors would like to thank the anonymous referees for several suggestions for the improvement of this paper. This work is supported by the Fundamental Research Funds for the Central Universities of China (Grant no. JGK101677).

References

1 Black F. and Scholes M., The pricing of options and corporate liabilities, Journal of Political Economy. (1973) 81, 637–659.
10.1086/260062
Web of Science® Google Scholar
2 Merton R. C., Theory of rational option pricing, The Rand Journal of Economics. (1973) 4, 141–183, 0496534.
Google Scholar
3 Leland H. E., Option pricing and replication with transaction costs, Journal of Finance. (1985) 40, 1283–1301.
10.1111/j.1540-6261.1985.tb02383.x
Web of Science® Google Scholar
4 Palmer K., A note on the Boyle—vorst discrete-time option pricing model with transactions costs, Mathematical Finance. (2001) 11, no. 3, 357–363, 2-s2.0-0035612326.
10.1111/1467-9965.00120
Web of Science® Google Scholar
5 Hoggard T., Whalley A. E., and Wilmott P., Hedging option portfolios in the presence of transaction costs, Advanced Futures and Options Research. (1994) 7, 21–35.
Google Scholar
6 Barles G. and Soner H. M., Option pricing with transaction costs and a nonlinear Black-Scholes equation, Finance and Stochastics. (1998) 2, no. 4, 369–397, https://doi.org/10.1007/s007800050046, 1809526, ZBL0915.35051.
10.1007/s007800050046
Google Scholar
7 Jandačka M. and Ševčovič D., On the risk-adjusted pricing-methodology-based valuation of vanilla options and explanation of the volatility smile, Journal of Applied Mathematics. (2005) no. 3, 235–258, https://doi.org/10.1155/JAM.2005.235, 2201973, ZBL1128.91025.
10.1155/JAM.2005.235
Google Scholar
8 Frey R. and Patie P., Risk management for derivatives in illiquid markets: a simulation study, Advances in Finance and Stochastics, 2002, Springer, Berlin, Germany, 137–159, 1929376, ZBL1002.91031.
10.1007/978-3-662-04790-3_8
Google Scholar
9 Sircar K. R. and Papanicolaou G., General Black-Scholes models accounting for increased market volatility from hedging strategies, Applied Mathematical Finance. (1998) 5, 45–82.
10.1080/135048698334727
Google Scholar
10 Liu H. and Yong J., Option pricing with an illiquid underlying asset market, Journal of Economic Dynamics & Control. (2005) 29, no. 12, 2125–2156, https://doi.org/10.1016/j.jedc.2004.11.004, 2185277, ZBL1198.91210.
10.1016/j.jedc.2004.11.004
Web of Science® Google Scholar
11 Avellaneda M., Levy A., and Paras A., Pricing and hedging derivative securities in markets with uncertain volatilities, Applied Mathematical Finance. (1995) 2, 73–88.
10.1080/13504869500000005
Google Scholar
12 Hodges S. D. and Neuberger A., Optimal replication of contingent claims under transaction costs, Review of Future Markets. (1989) 8, 222–239.
Google Scholar
13 Boyle P. P. and Tian Y., An explicit finite difference approach to the pricing of barrier options, Applied Mathematical Finance. (1998) 5, 19–43.
10.1080/135048698334718
Google Scholar
14 Zvan R., Forsyth P. A., and Vetzal K. R., A General Finite Element Approach for PDE Option Pricing Models, 1998, University of Waterloo, Ontario, Canada.
Google Scholar
15 Vázquez C., An upwind numerical approach for an American and European option pricing model, Applied Mathematics and Computation. (1998) 97, no. 2-3, 273–286, https://doi.org/10.1016/S0096%2D3003(97)10122%2D9, 1643127.
10.1016/S0096-3003(97)10122-9
Web of Science® Google Scholar
16 Tangman D. Y., Gopaul A., and Bhuruth M., Exponential time integration and Chebychev discretisation schemes for fast pricing of options, Applied Numerical Mathematics. (2008) 58, no. 9, 1309–1319, https://doi.org/10.1016/j.apnum.2007.07.005, 2444259, ZBL1151.91546.
10.1016/j.apnum.2007.07.005
Web of Science® Google Scholar
17 Wade B. A., Khaliq A. Q. M., Yousuf M., Vigo-Aguiar J., and Deininger R., On smoothing of the Crank-Nicolson scheme and higher order schemes for pricing barrier options, Journal of Computational and Applied Mathematics. (2007) 204, no. 1, 144–158, https://doi.org/10.1016/j.cam.2006.04.034, 2320203, ZBL1137.91477.
10.1016/j.cam.2006.04.034
Web of Science® Google Scholar
18 Sevcovic D., Stehlikova B., and Mikula K., Analytical and Numerical Methods for Pricing Financial Derivatives, 2011, Nova Science, Hauppauge, NY, USA.
Google Scholar
19 Kútik P. and Mikula K., Finite volume schemes for solving nonlinear partial differential equations in financial mathematics, Finite Volumes for Complex Applications. VI. Problems & Perspectives, 2011, 4, Springer, Heidelbergm, Germnay, 643–651, Springer Proceedings in Mathematics., https://doi.org/10.1007/978%2D3%2D642%2D20671%2D9_68, 2882342, ZBL1246.91150.
10.1007/978-3-642-20671-9_68
Google Scholar
20 Company R., Jódar L., and Pintos J.-R., A numerical method for European option pricing with transaction costs nonlinear equation, Mathematical and Computer Modelling. (2009) 50, no. 5-6, 910–920, https://doi.org/10.1016/j.mcm.2009.05.019, 2569252, ZBL1185.91174.
10.1016/j.mcm.2009.05.019
Google Scholar
21 Company R., Jódar L., and Pintos J.-R., Consistent stable difference schemes for nonlinear Black-Scholes equations modelling option pricing with transaction costs, Mathematical Modelling and Numerical Analysis. (2009) 43, no. 6, 1045–1061, https://doi.org/10.1051/m2an/2009014, 2588432, ZBL1175.91071.
10.1051/m2an/2009014
Web of Science® Google Scholar
22 Company R., Jódar L., Pintos J.-R., and Roselló M.-D., Computing option pricing models under transaction costs, Computers & Mathematics with Applications. (2010) 59, no. 2, 651–662, https://doi.org/10.1016/j.camwa.2009.10.028, 2575554, ZBL1189.91203.
10.1016/j.camwa.2009.10.028
Web of Science® Google Scholar
23 Yousuf M., Khaliq A. Q. M., and Kleefeld B., The numerical approximation of nonlinear Black-Scholes model for exotic path-dependent American options with transaction cost, International Journal of Computer Mathematics. (2012) 89, no. 9, 1239–1254, https://doi.org/10.1080/00207160.2012.688115, 2934804.
10.1080/00207160.2012.688115
Web of Science® Google Scholar
24 Cox S. M. and Matthews P. C., Exponential time differencing for stiff systems, Journal of Computational Physics. (2002) 176, no. 2, 430–455, https://doi.org/10.1006/jcph.2002.6995, 1894772, ZBL1005.65069.
10.1006/jcph.2002.6995
CAS Web of Science® Google Scholar
25 Düring B., Fournié M., and Jüngel A., High order compact finite difference schemes for a nonlinear Black-Scholes equation, International Journal of Theoretical and Applied Finance. (2003) 6, no. 7, 767–789, https://doi.org/10.1142/S0219024903002183, 2019728, ZBL1070.91024.
10.1142/S0219024903002183
Google Scholar
26 Dremkova E. and Ehrhardt M., A high-order compact method for nonlinear Black-Scholes option pricing equations of American options, International Journal of Computer Mathematics. (2011) 88, no. 13, 2782–2797, https://doi.org/10.1080/00207160.2011.558574, 2826512, ZBL1237.91228.
10.1080/00207160.2011.558574
Web of Science® Google Scholar
27 Burchard H., Deleersnijder E., and Meister A., A high-order conservative Patankar-type discretisation for stiff systems of production-destruction equations, Applied Numerical Mathematics. (2003) 47, no. 1, 1–30, https://doi.org/10.1016/S0168%2D9274(03)00101%2D6, 2003144, ZBL1028.80008.
10.1016/S0168-9274(03)00101-6
Web of Science® Google Scholar
28 Dimitrov D. T. and Kojouharov H. V., Positive and elementary stable nonstandard numerical methods with applications to predator-prey models, Journal of Computational and Applied Mathematics. (2006) 189, no. 1-2, 98–108, https://doi.org/10.1016/j.cam.2005.04.003, 2202966, ZBL1087.65068.
10.1016/j.cam.2005.04.003
Web of Science® Google Scholar
29 Dang Q. A. and Ehrhardt M., Adequate numerical solution of air pollution problems by positive difference schemes on unbounded domains, Mathematical and Computer Modelling. (2006) 44, no. 9-10, 834–856, https://doi.org/10.1016/j.mcm.2006.02.016, 2253755, ZBL1137.65395.
10.1016/j.mcm.2006.02.016
Web of Science® Google Scholar
30 Chen-Charpentier B. M. and Kojouharov H. V., An unconditionally positivity preserving scheme for advection-diffusion reaction equations, Mathematical and Computer Modellinghttps://doi.org/10.1016/j.mcm.2011.05.005.
10.1016/j.mcm.2011.05.005
Google Scholar
31 Fichera G., Sulle equazioni differenziali lineari ellittico-paraboliche del secondo ordine, Atti della Accademia Nazionale dei Lincei. (1956) 5, 1–30, 0089348, ZBL0075.28102.
Google Scholar
32 Golub G. H. and Van Loan C. F., Matrix Computations, 1996, 3rd edition, Johns Hopkins University Press, Baltimore, Md, USA, Johns Hopkins Studies in the Mathematical Sciences, 1417720.
CAS Web of Science® Google Scholar

Citing Literature

All articles

A Positivity-Preserving Numerical Scheme for Nonlinear Option Pricing Models

Abstract

1. Introduction

2. The Transformed Problem

3. The Unconditionally Positivity-Preserving Scheme