Choosing Improved Initial Values for Polynomial Zerofinding in Extended Newbery Method to Obtain Convergence
Abstract
In all polynomial zerofinding algorithms, a good convergence requires a very good initial approximation of the exact roots. The objective of the work is to study the conditions for determining the initial approximations for an iterative matrix zerofinding method. The investigation is based on the Newbery′s matrix construction which is similar to Fiedler′s construction associated with a characteristic polynomial. To ensure that convergence to both the real and complex roots of polynomials can be attained, three methods are employed. It is found that the initial values for the Fiedler′s companion matrix which is supplied by the Schmeisser′s method give a better approximation to the solution in comparison to when working on these values using the Schmeisser′s construction towards finding the solutions. In addition, empirical results suggest that a good convergence can still be attained when an initial approximation for the polynomial root is selected away from its real value while other approximations should be sufficiently close to their real values. Tables and figures on the errors that resulted from the implementation of the method are also given.
1. Introduction
The paper is organized as follows.
In Section 2, we have reviewed the iterative methods which have been used for finding roots of polynomials. In Section 3, the basis of the Fiedler’s theorems is reviewed. In Section 4, we have introduced Fiedler’s method by considering the initial values of Schmeisser’s method. In Sections 5 and 6, we have illustrated the solutions of polynomials by considering the initial values from a section of the complex plane and initial values from the circle with a certain radius, R. In Section 7, we have presented the results of choosing initial values for arbitrary degree polynomial in the Fiedler’s method to attain the convergence of the roots.
It is to be noted that in Sections 4, 5, 6, and 7 the tables given indicate the accuracy of our results. Moreover, the errors of the methods are shown by the figures. Importantly, in order to implement our methods and to obtain the results as illustrated by the figures and tables, we have utilized Matlab and Maple software. In Section 8, the analysis of the results is discussed. Finally, in Section 9, the conclusion of this research is given.
2. Review on Existing Methods
Graeffe’s root-squaring method replaces the given polynomial by another polynomial whose roots are the squares of the original polynomial. Newton’s method is an iterative procedure based on a Taylor series of the polynomial about the approximate root.
As for the study by Foster [3]: “Convergence requires a very good initial approximation of the exact root.” The algorithm of Jenkins and Traub involves three stages and the roots have to be computed in an approximately increasing order of magnitude in order to avoid instability that arises when deflating with a large root [4, 5]. The Laguerre’s method has cubic convergence for simple roots and also has linear convergence for multiple roots but each iteration requires that the first and second derivatives be evaluated at the estimated root, which makes the method computationally expensive [3, 6]. Trefethen and Toh [5, 7] studied on the convergence between roots of a given polynomial and eigenvalues of the Frobenius companion matrix [8] and also Traub and Reid have shown that these two sets are comparable.
For the case of polynomials with repeated roots, Hull and Mathon [9] presented an iterative polynomial zerofinding algorithm such that the iterations not only converge to simple roots but also converge to multiple roots. In 2005 Yan and Chieng [10] introduced a method that theoretically resolves the multiple-root issue. The proposed method adopts the Euclidean algorithm to obtain the greatest common divisor (GCD) of a polynomial and its first derivative. The multiple roots are then defaulted into simple ones and then the multiplicities of the roots are determined and calculated accordingly by applying conventional root-finding methods. In 2007, Winkler [11] denoted that GCD computations by Uspensky’s algorithm enable the multiplicity of each root to be calculated, and the initial estimates of the roots of a polynomial are obtained by solving several lower degree polynomials, all of whose roots are simple.
In some work, pejorative manifold have been applied. For example, Zeng [12] presented an algorithm which transforms the singular root-finding problem into a regular nonlinear least squares problem on a pejorative manifold and calculates multiple roots simultaneously from a given multiplicity structure and initial root approximations.
Besides stability considerations in most of the conventional zerofinding methods, convergence requires a good initial approximation of the exact roots. In this study, we consider the importance of choosing good initial approximation of the roots to ensure that convergence is attained. We present generally how to choose initial values by applying Fiedler’s theorems and remarks, and the hybrid between Schmeisser’s and Fiedler’s methods. The work partly focuses on the comparison of errors between the Schmeisser’s method and the Schmeisser-Fiedler’s method when the initial values for the Fiedler’s method are generated from the Schmeisser’s method, for solving the same polynomial. Moreover, this study also discusses the error of finding roots of a polynomial by using the Fiedler’s method, choosing initial values on a complex plane and on a circle. However, Malek and Vaillancourt [13] has similarly investigated on the finding of the roots of polynomials by choosing the initial values through the mentioned ways without paying attention to the comparison and condition of choosing desired initial values. In this study, we have especially investigated on the effects of attaining convergence, despite choosing only one initial value that is not sufficiently close to its exact value. The upcoming tables and figures show the associated error of the corresponding computations. What is more, the polynomials used in this research are not restricted to only a particular class of polynomials. It is also highlighted that one of the main tasks of this research is the implementation of all the methods that we have described here for solving polynomials and drawing related figures by Matlab and Maple software.
3. Fiedler’s Method
The basis of Fiedler’s method is a reflection of an important theorem in linear algebra: all roots of the characteristic polynomial of a real symmetric matrix are real. In fact, Fiedler’s method is Newbery’s expanded method [14] and it determines real symmetric matrix for polynomial with real roots. Required initial values in Fiedler’s method are chosen by some different ways: from the initial values supplied by Schmeisser’s method, randomly taken from a region in the complex plane, or from a circle with a large radius.
In the method of Fiedler, there are some important theorems for obtaining the companion matrix which are given as Theorems 3.1, 3.2, and 3.5 below. In fact, Fiedler’s Theorem is an advantage of general theorem described below.
Theorem 3.1 (see [15].)For n ≥ 1, assume that b1, b2, …, bn are n distinct numbers and
For i, k = 1,2, …, n, let A = diag (−w(bk)/u(bk)), and let C = (cik) such that
Then for each t with v(t) ≠ 0, the number −w(t)/V(t) is an eigenvalue of (u(t)/V(t))A − δDCD and dk/(t − bk) is the corresponding eigenvector.
We present the important result of the above theorem as follows.
Result 1. It is seen that by the selection of t0 as a root of u(t) in the above theorem, the matrix δDCD will have an eigenvalue given by − w(t0)/V(t0) and this number will be equal to t0 if unitary polynomials u(x) and w(x) are assumed such that w(x) = x[u(x) − v(x)] since we can write −w(t0)/V(t0) = − t0[u(t0) − V(t0)]/V(t0) = t0.
Theorem 3.2 (see [16], Fiedler’s Theorem.)Assume that u(x) is a unitary polynomial of degree n > 1, and b1, …, bn ∈ C are n distinct numbers such that u(bk) ≠ 0 for k = 1,2 … , n. Consider
-
,
-
If roots of u are distinct and real and b1, …, bn are approximations of the roots, then δ can be chosen as +1 or −1 in such a way that dk ∈ ℝ, thus A is real symmetric [16].
Remark 3.3. If u(x) and bk are all real then each dk is real or imaginary.
Remark 3.4. Schmeisser [16] have proved that if the roots of u are distinct and single and the numbers b1, …, bn are approximations of these roots, then the matrix A in Theorem 3.2 is a unitary matrix.
Theorem 3.5 (see [14].)Let u(x) be a unitary polynomial of n ≥ 1 such that
If all the roots of u(x) are simple and real and bk is approximation of these roots, then A is real and symmetric, that is, AT = A ∈ Rn × n. Thus the matrix A is similar to Newbery’s matrix.
According to the aforementioned theorems and remarks, we can find the roots of polynomials with estimating initial values b1, …, bn by using the methods of Fiedler and Schmeisser and also by generating the companion matrix A, where A = B − δddt ∈ Cn × n and by the definition dk as the root of δV′(bk) − u(bk) = 0. We present some examples of solving polynomials by applying Fiedler’s Theorem and Schmeisser’s method. Further, we will examine the condition when only one of the approximations of the roots is far from its real value. For future study, we will go through another approach for estimation of the roots without much restriction and without compromising the convergence of the method to the exact solutions with a high degree of accuracy.
4. Hybrid of Fiedler’s Method and Schmeisser’s Method
Schmeisser [16] generated a symmetric tridiagonal matrix, T, by using a modified Euclidean algorithm. According to Schmeisser’s theorem which is based on a modified Euclidean algorithm and the matrix T, we implemented the related algorithm using Matlab for solving monic polynomials. Consider a monic polynomial U(x) and the corresponding matrix T, after solving, det (T − λI) = (−1)nU(λ), we obtain the roots of U(x) approximately. In this method, we consider the obtained values of Schmeisser’s method as the desired initial values for Fiedler’s method.
Example 4.1. Consider the Wilkinson polynomial as follows:
| Roots of u(x) | Initial values of b[i] | Eigenvalues of U | Schmeisser error | Fiedler error |
|---|---|---|---|---|
| 1 | 0.99999999965 | 0.99999999988800000663 | 0.00E − 15 | 1.199E − 9 |
| 2 | 1.99999999999 | 1.99999999680000058 | 5.33E − 15 | 3.199E − 10 |
| 3 | 2.99999999998 | 2.9999999999359999597 | 2.66E − 15 | 6.400E − 10 |
| 4 | 3.99999999999 | 3.999999999679999014 | 1.421E − 14 | 3.20E − 10 |
| 5 | 5.00000000001 | 4.999999999999999988 | 2.66E − 15 | 1.200E − 17 |
| 6 | 6.00000000001 | 5.999999999999999626 | 0.00E − 15 | 3.74E − 16 |
| 7 | 7.00000000007 | 6.999999999999999984 | 1.68E − 14 | 1.600E − 17 |
| 8 | 8.00000000004 | 7.999999999999999551 | 1.15E − 14 | 4.490E − 16 |
| 9 | 9.00000000005 | 8.999999999999999997 | 3.55E − 15 | 3.000E − 18 |
| 10 | 10.00000000001 | 9.999999999999998875 | 1.78E − 15 | 1.125E − 15 |
| 11 | 11.00000000001 | 10.999999999999999904 | 5.33E − 15 | 9.600E − 16 |
| 12 | 12.00000000001 | 12.00000000000000001 | 7.11E − 15 | 1.000E − 17 |
| 13 | 13.00000000002 | 12.99999999999999974 | 5.33E − 15 | 2.600E − 16 |
| 14 | 14.00000000002 | 14.00000000000000019 | 1.78E − 15 | 1.900E − 16 |
| 15 | 15.00000000002 | 14.99999999999999982 | 7.11E − 15 | 1.800E − 16 |
| 16 | 16.00000000002 | 15.99999999999999977 | 1.776E − 14 | 2.300E − 16 |
| 17 | 17.00000000002 | 16.99999999999999949 | 3.55E − 15 | 5.100E − 16 |
| 18 | 18.00000000002 | 17.99999999999999949 | 7.11E − 15 | 5.100E − 16 |
| 19 | 19.00000000002 | 18.99999999999999977 | 1.421E − 14 | 2.230E − 15 |
| 20 | 20.00000000002 | 19.99999999999999916 | 2.487E − 14 | 8.400E − 16 |
Now, the error chart for the obtained results is given in Figure 1.
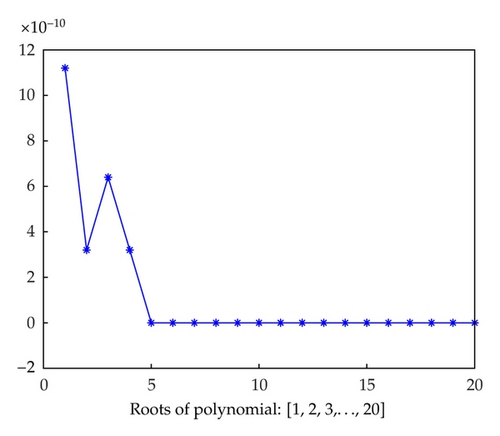
The second column of Table 1 gives the eigenvalues of the matrix generated by Schmeisser’s method. These values correspond to the respective roots of the given polynomial, when applying Schmeisser’s method. Subsequently, the values which are obtained by Schmeisser’s method are used in Fiedler’s method as initial approximations of the roots and the eigenvalues of the associated companion matrix A are then obtained. From row four to the last row of Table 1, it is clearly shown that the errors of solving the polynomial by Schmeisser’s method are higher than the errors accumulated from applying Fiedler’s method in which the desired initial values are acquired from Schmeisser’s method. Likewise, Figure 1 shows that the errors of Fiedler’s method by applying Schmeisser’s method for roots greater than 5 in Wilkinson polynomial decrease.
5. Fiedler’s Method Initial Values from a Section of the Complex Plane
In this method, we choose the initial values of Fiedler’s method taken from a section of the complex plane.
Example 5.1. Consider the polynomial u(x) = (x − i)(x − 2i)(x − 3i)(x − 4i)(x − 5i).
Using this method, we obtain the roots of this polynomial and the results are shown in Table 2.
The error chart is depicted in Figure 2.
The second column of Table 2 gives the approximated values of the roots when the initial values for solving polynomial of Example 5.1 are chosen from a complex plane using Fiedler’s method. Working on the generated matrix U, it was found that its eigenvalues converge to the respective real roots of the polynomial in the third column of Table 2. Referring to the fourth column, the errors of this method are adequately small in comparison with the real roots. Figure 2 depicts the results in Table 2, as well.
| Roots of u(x) | Initial values of b[i] | Eigenvalues of matrix U | Fiedler-error |
|---|---|---|---|
| 1i | 0.99999999999432932 i | 0.0 + 5.670 i E − 12 | |
| 2i | 2 + i | 1.99999999968706632 i | 0.0 + 3.129 i E − 10 |
| 3i | 7 + 3i | 8.122 × 10−191 + 2.9999999987826582 i | 0.0 + 1.217 i E − 10 |
| 4i | 4.0000000000806822 i | 0.0 + 8.68 i E − 12 | |
| 5i | 1 + 3i | 4.99999999982455368 i | 0.0 + 1.754 i E − 10 |

6. Fiedler’s Method with Initial Values from a Circle with R Radius
In this method, we choose the initial values of Fiedler’s method from a circle with radius R. It should be taken care that the approximations converge to smaller roots if R is considered to be sufficiently large (R > 10), and the method converges to larger roots if R is assumed to be adequately small R < 1).
Example 6.1. Consider the polynomial u(x) = (x − 11) (x − 12) (x − 13) (x − 14) using this method, R = 10 is chosen and we obtain the roots.
The results are shown in Table 3.
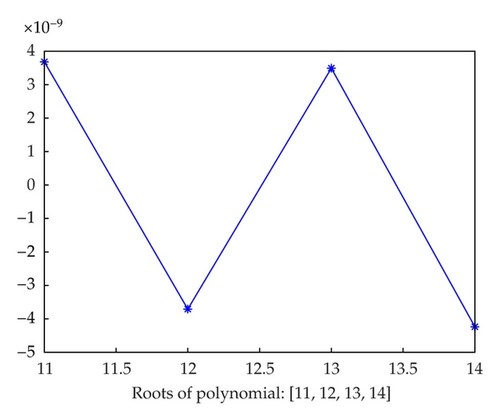
The error chart is depicted in Figure 3.
In Table 3, the second column points out the desired initial values for solving polynomial given in Example 6.1 by applying Fiedler’s method. They were taken from the circle with radius R = 10. After computing the eigenvalues of matrix U, given in the third column of Table 3, each corresponding to the respective roots of the polynomial, the errors of the method were satisfactorily small in comparison with real roots. Figure 3 illustrates the results in Table 3, as well.
| Roots of u(x) | Initial values of b[i] | Eigenvalues of matrix U | Fiedler error |
|---|---|---|---|
| 11 | 1 + 3 i | 11.000000036818370 | 3.681 E − 8 |
| 12 | −1 − 3 i | 11.9999999996290109 | 3.709 E − 8 |
| 13 | 13.0000000034938808 | 3.493 E − 8 | |
| 14 | 13.9999999957633268 | 4.236 E − 8 |
7. Approximation of Initial Values for Fiedler’s Method for Arbitrary Degree Polynomial
In this part, after a set of research about the polynomial with each degree, we obtained that if we want to choose the initial values b1, b2, …, bn we are allowed to choose one of the roots to be away from the real roots but the others must be close to the real ones.
Example 7.1. Consider the below polynomial:
The error chart for the results obtained is given in Figure 4.
| Roots of u(x) | Initial values of b[i] | Eigenvalues of matrix U | Fiedler error |
|---|---|---|---|
| 1 | 3.9 | 0.99999999999961600 | 5.293 E − 11 |
| 2 | 13.3 | 1.99999999999998450 | 1.023 E − 7 |
| 3 | 2.1 | 2.99999999999999287 | 2.476 E − 11 |
| 4 | 1.5 | 3.9999999999999702 | 1.524 E − 11 |
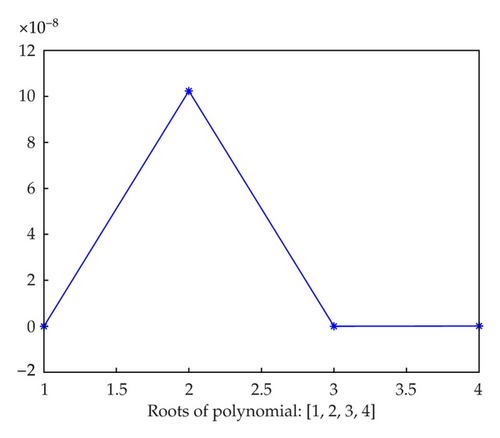
In Table 4, the second column shows the desired initial values for solving the polynomial, given in Example 7.1, by applying Fiedler’s method. In the second row, the amount of 13.3 is taken away from the exact value. In the third column, the eigenvalues of the matrix U which corresponds to the respective roots of polynomial are shown. The results are appropriately close to the real roots. Figure 4 illustrates the results in Table 4, as well.
8. Discussion
Many numerical methods, using linear algebra, linear programming, and Fourier analysis, have been developed for the solution of the polynomial (1.1). In this stage, we describe the disadvantages of the present methods and explain the findings of our results in the form of tables and figures.
Considering the disadvantages of the zerofinding methods, Winkler mentioned that the Graeffe’s root-squaring method fails when there are roots of equal magnitudes [11, p. 3]; however, by applying Fiedler’s method the algebraic equations which have roots with almost the same modulus can be solved [17]. In addition, Bairstow’s method is only valid for polynomials containing real coefficients avoiding complex arithmetic. Moreover, the algorithm of Jenkins and Traub also involves three stages and is only valid for polynomials with real coefficients. Another insufficient method like Laguerre’s technique is not completely perfect whereby each iteration requires that the first and second derivatives be evaluated at the estimated root, which makes the method computationally expensive. Muller’s method is a variant of Newton’s method and convergence in Newton’s method requires that the estimate be sufficiently near the exact root.
It can be gathered that the above methods have been facing some issues which need to be reviewed. The information in Table 1 shows that after choosing the desired initial values from the results obtained by Schmeisser’s method, the third column of Table 1, the approximate results are reasonable, having the accuracy of nearly 10−10 after ten iterations. By comparing the results in columns 4 and 5 of Table 1, it reveals that the Fiedler’s method, assuming the desired initial values taken from obtained values of Schmeisser’s method, is more accurate than solving the polynomial by Schmeisser’s method entirely.
It can be seen that 75 percent of the roots have accuracy up to almost 10−16. Similarly, Figure 1 also verifies that in case of roots which are greater than 5 the error of Fiedler’s method in which Schmeisser’s method is applied steadily decreases.
The information in Table 2 points out the estimated initial values which are chosen of a complex plane. The results obtained by Fiedler’s method in Example 4.1 are reasonable and nearly have accuracy of 10−11. Figure 2 confirms the same results as well.
Choosing suitable initial values on the circle with R = 10 in Example 6.1 along with comparison of the third column in Table 3 and the real roots of the polynomial concludes that the results which were found by using this method are reasonable. These results roughly have accuracy of 10−14. Likewise, Figure 3 confirms the similar findings.
In the second column of Table 4 while the real roots are {1, 2, 3, 4}, only one of approximation of the roots is chosen away from the exact value. In Example 7.1, we have considered an initial value approximately equals 13.3 for the real root 2. According to the third column of Table 4, the eigenvalues of matrix U correspond to the roots of polynomial. the results were adequately close to the real roots with an accuracy of 10−10. Similarly, Figure 4 also proves this statement.
9. Conclusion
Fiedler’s different algorithms are described. As mentioned earlier, it can be seen that among existing numerical algorithms, we are not able to say that there is a special algorithm for every arbitrary polynomial that is better than other ones and also there are the zerofinding explicit formulas for maximum fifth-degree polynomial. In order to find the roots of an arbitrary polynomial, we could find the roots of polynomial with high accuracy by using one of the algorithms presented in this paper. In the case of using these algorithms for choosing the initial values, we are able to choose these values from Schmeisser’s method or by selection from a square or circle or by an arbitrary selection that all values must be closed to the real ones except for one of them. In addition, besides stability considerations, in future work we are interested to find the root-finding algorithms with less limitation of good initial approximation of the roots to ensure convergence besides stability considerations. In this case, future studies should consider whether we can find an approach of polynomial zerofinding which ensures convergence to the roots even though some of the initial values may not necessarily be closed to the real roots.
Acknowledgments
The authors would like to acknowledge UTM Research University Grant, vote no. Q.J130000.7126.04J05, Ministry of Higher Education (MOHE), Malaysia, for supporting the research. The authors are thankful to the referees for their constructive comments which improved the presentation of the paper.




