Volume 2012, Issue 1 158983

Research Article

Open Access

Vibration of an Offshore Structure Having the Form of a Hollow Column Partially Filled with Multiple Fluids and Immersed in Water

Hsien-Yuan Lin,

Corresponding Author

Hsien-Yuan Lin

[email protected]

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

Jeng-Nan Lee,

Jeng-Nan Lee

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

Wen-Hao Sung,

Wen-Hao Sung

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

Hsien-Yuan Lin,

Corresponding Author

Hsien-Yuan Lin

[email protected]

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

Jeng-Nan Lee,

Jeng-Nan Lee

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

Wen-Hao Sung,

Wen-Hao Sung

Department of Mechanical Engineering, Cheng Shiu University, Kaohsiung 83347, Taiwan csu.edu.tw

Search for more papers by this author

First published: 26 September 2012

https://doi.org/10.1155/2012/158983

Citations: 1

Academic Editor: Carl M. Larsen

Share a link

Email
Wechat
Bluesky

Abstract

This paper employs the numerical assembly method (NAM) to determine the exact frequency-response amplitudes of an offshore structure such as piles or towers having the form of a hollow column filled with multiple fluids, immersed in water, carrying an eccentric tip mass supported by a translational spring and/or a rotational spring, and subjected to a harmonic force. The hollow column is modeled as a Bernoulli-Euler cantilever beam fixed at the bottom. For the case of zero harmonic force, the simultaneous equations of the vibration system reduce to an eigenvalue problem so that the natural frequencies and mode shapes of the beam can also be obtained. The effect of height of filled fluids on the characteristics of free vibration is also presented.

1. Introduction

In offshore engineering, structures such as towers or piles immersed in water can be predicted with rational accuracy from a fixedly supported beam with a tip mass. Many important papers [1–5] have been published in the field. Those researches was assumed that the beam was solid or empty hollow. Chan and Zhang [6] presented the natural frequency of a cantilever tube filled with only one liquid by using the continuity and equilibrium conditions at the liquid level position. Amabili [7] studied the free vibration of circular cylindrical shells and tubes completely filled with one dense fluid and partially immersed in one different fluid. Wu at el. [8–10] used three different methods to present the natural frequencies and mode shapes of an immersed solid beam carrying an eccentric tip mass with rotary inertia. Lin [11–13] presented the exact natural frequencies and mode shape of a beam carrying multiple concentrated elements.

From the foregoing literature review one finds that the literature regarding determination of the natural frequencies and mode shapes of a hollow beam (partially or completely) filled with fluids of different densities and (partially or completely) immersed in different fluids is little. In this paper an accurate method is presented to determine the natural frequencies and mode shapes of an immersed hollow beam filled with fluids of different densities and carrying an eccentric tip mass supported by a rotational spring and a translational spring. The vibration characteristics of the beam system subjected to a harmonic force are also presented.

In the exploratory offshore drilling operations, the long slender vertical cylindrical pipe placed between the sea surface and the ocean floor for conveying various fluids is called “riser.” In the existing literature concerning the analyses of marine risers [14], the fluids in the “riser” are assumed to be uniform with constant mass density for simplicity. In practice, the last assumption may be different from the actual situations to some degree, because the riser pipe may be filled with several fluids with different mass densities simultaneously, such as water, gas, oil, or clay. For this reason, this paper tries to present a technique to study the dynamic behaviors of a pipe filled with multiple fluids and immersed in water. Because the presented mathematical model is closer to the marine risers, it is believed that more satisfactory results will be obtained.

In order to confirm the reliability of the presented approach, the numerical example illustrated in this paper is also conducted by using the FEM and good agreement is achieved. One of the predominant merits for the presented approach is that its numerical results belong to the “exact solutions” and may be the benchmark for evaluating the accuracy of the other approximate methods (such as FEM).

2. Theoretical Model

Figure 1 shows the sketch of a immersed hollow beam filled with fluids of different densities and carrying an eccentric tip mass with rotary inertia, rotational spring, and translational spring supports. The points corresponding to the locations of fluid interfaces and/or applied concentrated forces are referred to as “stations.” The positions of stations are defined by x_n(n = 1, …, n) and the subscript of x_n refer to the numbering of the stations. Symbol “⊗” denotes the center of mass of the tip mass. E is Young’s modulus of the beam, I is moment of inertia of the cross-sectional area of the beam, d_o and d_s are outer and inner diameters of the hollow beam, respectively, is mass per unit length of the beam, ρ_t, ρ_o, and ρ_s are the density of the stainless steel beam, density of the outer fluid (water) of the hollow beam, and density of the filled fluids of the hollow beam, respectively. M_e is the tip mass, J_e is its moment of inertia, k_Te is the translational spring constant of supporting tip mass, k_Re is the rotational spring constant of supporting tip mass, e_m is the distance between the upper end of beam and center of gravity of the tip mass, and e_k is the distance between the upper end of beam and the translational spring support.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The sketch of an immersed hollow beam filled with fluids of different densities, subjected to a force, and carrying an eccentric tip mass supported by a translational and a rotational spring.

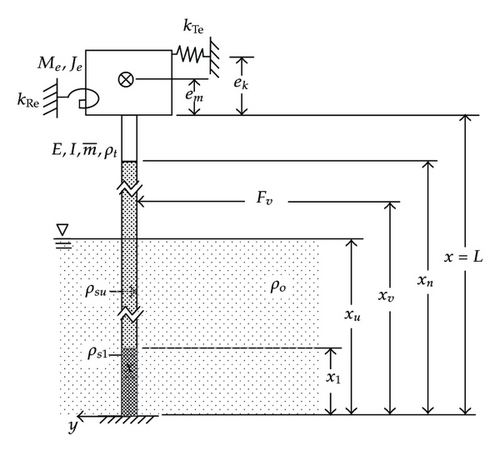
2.1. Equation of Motion and Displacement Function

The differential equation of motion for the ith beam segment of a uniform immersed hollow beam filled with fluids of different densities, subjected to a harmonic force, and carrying an eccentric tip mass supported by a rotational spring and a translational spring (cf. Figure 1) with small deflections is given by

()

with

, and

given by

()

where

, and

are the mass per unit length of the ith beam segment, outer fluid (added) mass per unit length of the ith beam segment, and filled fluid (added) mass per unit length of the ith beam segment, respectively, y_i(x, t) is the transverse displacement at position x and time t for the ith beam segment, and F(t) is a force at time t. Besides, δ(x − x_i) is the Dirac delta with x_i denoting the coordinate at which the concentrated force F(t) is applied.

If the applied concentrated force takes the form

()

then, in the steady state, one has

()

where Y_i(x) is the amplitude of y_i(x, t), ω_e is the exciting frequency of the applied harmonic forces,

is amplitude of F(t), and

Substitution of (2.6), (2.7) into (2.1) gives

()

where

()

Equation (2.8) is a nonhomogeneous equation, and its “complete” solution takes the form

()

in which C₁, C₂, C₃, and C₄ are the unknown integration constants. From (2.10), one sees that, for any beam segment on which no concentrated force F(t) being applied, its displacement function will take the form

()

2.2. Coefficient Matrix [B_u] for an Intermediate Fluid Interface

If the station numbering of an intermediate fluid interface is u, then the continuity of deformations and the equilibrium of moments and forces at station u require that

()

Substitution of (2.11) into (2.12)–(2.15) leads to

()

Writing (2.17)–(2.20) in matrix form, one has

()

where

()

In the above equations (2.25) and (2.26), the symbols, [] and {}, denote the rectangular matrix and column vector, respectively. The coefficient matrix [B_u] is placed in (A.1) of Appendix A.

2.3. Coefficient Matrix [B_v] for an Intermediate Applied Force

If the station numbering for the intermediate harmonic concentrated force normal to the beam is v, then the continuity of deformations and equilibrium of moments and forces require that

()

From (2.11), (2.27)–(2.30), one obtains

()

Writing (2.31)–(2.34) in matrix form, one has

()

And the coefficient matrix [B_v] is placed in (B.1) of Appendix B.

2.4. Coefficient Matrices [B₀] and [B_N] for the Two Ends of the Entire Beam

The lower end of hollow beam is fixed as shown in Figure 1, then the boundary condition is

()

From (2.11), (2.38), one obtains

()

where

()

If the tip of the beam is carrying an eccentric mass with rotary inertia, a rotational spring, and translational spring as shown in Figure 1, then the boundary conditions are

()

where

()

n is the total number of intermediate stations.

From (2.11) and (2.42)–(2.43), one obtains

()

Writing (2.45)–(2.46) in matrix form, one has

()

where

()

And the coefficient matrix [B_N] is placed in (C.1) of Appendix C.

2.5. Determination of Natural Frequencies and Mode Shapes of the Beam

The integration constants relating to the lower-end and upper-end supports of the beam are defined by (2.41) and (2.54), respectively, while those relating to the intermediate stations are defined by (2.26) and (2.36) depending upon the interface of fluid and/or the concentrated force being located there. The associated coefficient matrices are given by [B₀] (cf. (2.40)), [B_u](cf. (A.1) of Appendix A), [B_v] (cf. (B.1) of Appendix B) and [B_N] (cf. (C.1) of Appendix C). From the last equations concerned, one may see that the identification number for each element of the last coefficient matrices is shown on the top side and right side of each matrix. Therefore, using the numerical assembly technique, one may obtain a matrix equation for all the integration constants of the entire beam

()

For the case of free vibrations, the applied force amplitude

is zero and (2.55) reduces to

()

Nontrivial solution of (2.56) requires that its coefficient determinant is equal to zero, that is,

()

which is the frequency equation for the present problem.

In this paper, the incremental search method is used to find the natural frequencies of the vibrating system, ω_v (v = 1,2, …). With respect to each natural frequency ω_v, one may obtain the corresponding integration constants from (2.56). The substitution of the last integration constants into the displacement functions of the associated beam segments will determine the corresponding mode shape of the entire beam, Y^(v)(ξ).

2.6. Determination of Forced Vibration Response of the Beam

For the case of forced vibrations, from (2.55), one has

()

Thus, if the exciting frequency ω_e (or the associated dimensionless frequency parameter Ω_e) of the harmonic forces is given, then one may obtain the corresponding integration constants from (2.58). The substitution of last integration constants into the displacement functions of associated beam segments will determine the corresponding vibration amplitude |Y(ξ)|.

3. Numerical Results and Discussions

Before the vibration analysis of an immersed hollow beam filled with fluids of different densities, subjected to a force, and carrying an eccentric tip mass supported by a translational and a rotational spring is performed, the reliability of the theory and the computer program developed for this paper are confirmed by comparing the present results with those obtained from the existing literature.

3.1. Reliability of the Developed Computer Program

The first example studied is a fixedly supported immersed beam carrying tip mass with rotary inertia and eccentricity e = 0.5 m and two intermediate lumped masses kg located at x₂ = 13 m and x₃ = 14 m, respectively, for the case of draft ratio and water density ρ = 1000 Kg/m³. The dimensions of the solid beam are as follows: Young’s modulus = 2.068 × 10¹¹N/m², diameter d= 0.3 m, mass density ρ = 7850 Kg/m³, and total length L = 15 m. The lowest four natural frequencies of the immersed beam are shown in Table 1. From Table 1, one sees that the results of this paper are in good agreement with those of [9].

Table 1. The lowest four natural frequencies of a fixedly supported immersed beam carrying an eccentric tip mass and two intermediate lumped masses.

Methods	Parameters						Natural frequencies (rad/sec)
Methods							ω₁	ω₂	ω₃	ω₄
Present	13	14	0.1	0.1	0.1	0.1	2.5978	10.0440	42.3158	109.7077
[9]	13	14	0.1	0.1	0.1	0.1	2.5978	10.0441	42.3158	109.7078

3.2. Natural Frequencies and Mode Shapes of the Immersed Hollow Beam Filled with Two Kinds of Fluids Carrying an Eccentric Tip Mass with Rotary Inertia, Translational and Rotational Spring Supports

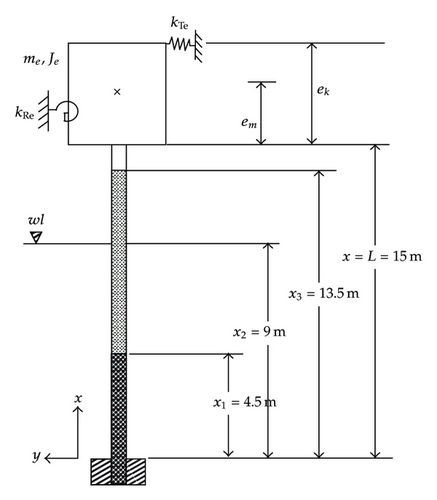
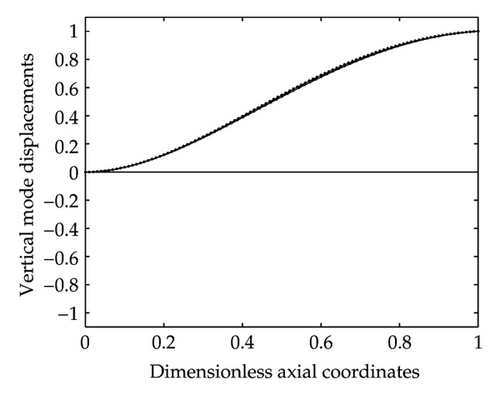
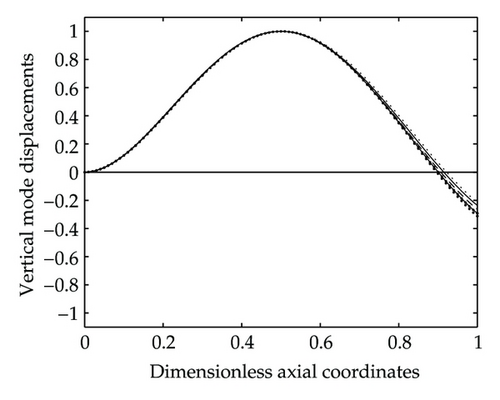
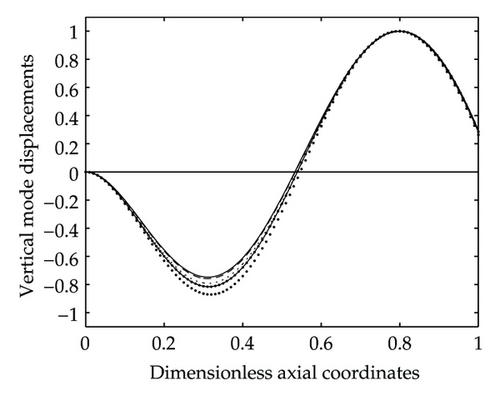
The second example studied is a immersed hollow beam filled with two kinds of fluids and carrying an eccentric tip mass with rotary inertia, translational and rotational spring supports (cf. Figure 2). The parameters of the steel hollow beam are as follows: total length L = 15 m, outer diameter d_o = 0.6 m, inner diameter m, Young’s modulus E = 2.068×10¹¹ N/m², density ρ_t = 7850 kg/m³, density of the inner upper fluids ρ_s2 = 1000 kg/m³, and density of the inner lower fluid ρ_s1 = 1400 kg/m³. The nondimensional parameters of the eccentric tip mass are as follows: mass ; rotary inertia of the tip mass ; constants of the rotational spring support ; constants of the translational spring support ; distance between the fixed point of the tip mass and its center of gravity ; distance between the fixed point of the tip mass and the translational spring support ; the nondimensional height of the beam immersed in water ; height of filled lower fluid ; height of filled with upper fluid , respectively. The lowest four natural frequencies and non-dimensional parameters for the hollow beam are shown in Table 2. In order to confirm the reliability of the presented results, the current example is also conducted by using the FEM with the lowest four natural frequencies shown in Table 2. From the table one sees that the lowest four natural frequencies of the hollow beam obtained from FEM are very close to those obtained from the presented approach; furthermore, they decrease with increasing the height of filled upper fluid due to its added mass. Corresponding to the four natural frequencies listed in Table 2, the lowest four mode shapes of the hollow beam are shown in Figures 3(a)–3(c), respectively, where (a), (b), and (c) refer to the 1st,2nd, and 3rd mode shapes of the hollow beam. Besides, the curves − − − −, — — — —, – – – –, …………, and −·−·− denote the mode shapes of the hollow beam filled with the upper fluid height , respectively.

Table 2. The lowest four natural frequencies of the immersed hollow beam filled with two kinds of fluids and carrying an eccentric tip mass with a translational and a rotational spring supports (cf. Figure 2).

Dimensionless parameters						Methods	Natural frequencies (rad/sec) (dimensionless frequency parameters (Ω))
							ω₁ (Ω₁)	ω₂ (Ω₂)	ω₃ (Ω₃)	ω₄ (Ω₄)
0.3	0.4	1	0.01	30	10	Present	24.6479 (2.8932)	71.9802 (4.9442)	159.2279 (7.3536)	268.8851 (9.5559)
0.3	0.5	1	0.01	30	10	Present	24.5520	69.9351	158.3664	267.6327
0.3	0.5	1	0.01	30	10	FEM	24.5521	69.9352	158.3665	267.6331
0.3	0.6	1	0.01	30	10	Present	24.3869	68.0844	158.2174	261.6957
0.3	0.6	1	0.01	30	10	FEM	24.3869	68.0844	158.2176	261.6961
0.3	0.7	1	0.01	30	10	Present	24.1460	66.9012	156.6135	256.6476
0.3	0.7	1	0.01	30	10	FEM	24.1460	66.9013	156.6136	256.6480
0.3	0.8	1	0.01	30	10	Present	23.8382	66.4282	153.3229	255.8103
0.3	0.8	1	0.01	30	10	FEM	23.8383	66.4283	153.3231	255.8107

3.3. Forced Vibration Responses of the Hollow Beam Filled with Two kinds of Fluids, Immersed in Water and Carrying an Eccentric Tip Mass

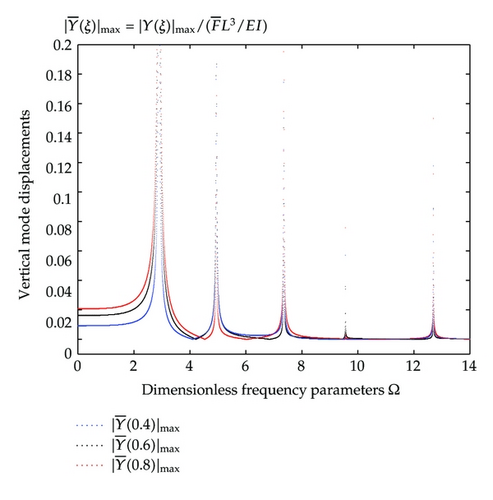
The beam system of the present example is the same as the last one but the beam subjected to a harmonic force is located at ξ = 0.8. For each value of Ω (from 0 to 13.0 with interval ΔΩ = 0.001), one may obtain the integration constants from (2.58). Then we compute the vibration amplitudes when it is placed in different locations on the beam. Figure 4 shows the relationship between the dimensionless frequency parameters (Ω) and the dimensionless response amplitudes for the points located at ξ = 0.4, 0.6, and 0.8, where the horizontal axis is the dimensionless frequency parameter (Ω) and the vertical axis is the dimensionless vibration amplitude (). The blue, black, and red curves are for points located at locations ξ = 0.4, 0.6, and 0.8, respectively. The vibration amplitudes for the point located at either ξ = 0.4, 0.6 or 0.8 have peaks when the dimensionless frequency parameter Ω≈ 2.9, 4.9, 7.4, 9.6, and 12.7. This is because when the dimensionless frequency parameter Ω is near any of the natural frequencies of the beam, as shown in the parenthesis of line 1 of Table 2, resonance appears.

4. Conclusion

The results presented in this work have found that one can obtain the lowest several “exact” natural frequencies and corresponding mode shapes of an immersed hollow beam partially filled with two kinds of fluids and carrying an eccentric tip mass with rotary inertia, rotational and translation spring supports. For the beam subjected to a harmonic force, one can determine the frequency-response curve for any point of the beam using this method. Because a peak will appear in each curve when the exciting frequency of the harmonic force is near any of natural frequencies of the beam, one can determine natural frequencies of the beam based on the peaks of any frequency-response curve.

Appendices

A.

Consider the following:

()

where 𝔅 denotes sinθ_u, ℭ denotes

, 𝔇 denotes

, 𝔈 denotes

, 𝔊 denotes cos θ_u, ℌ denotes

, ℑ denotes

, 𝔎 denotes

, 𝔄 denotes sinh θ_u, 𝔉 denotes

, 𝔐 denotes

, 𝔑 denotes

, 𝔒 denotes cosh θ_u, 𝔓 denotes

, 𝔔 denotes

, ℜ denotes

, 𝔖 denotes −sinθ_u+1, 𝔗 denotes

, 𝔘 denotes

, 𝔙 denotes

, 𝔚 denotes −cos θ_u+1, 𝔛 denotes

, 𝔜 denotes

, ℨ denotes

, 𝔞 denotes −sinh θ_u+1, 𝔟 denotes

, 𝔠 denotes

, 𝔡 denotes

, 𝔢 denotes −cosh θ_u+1, 𝔣 denotes

, 𝔤 denotes

, and 𝔥 denotes

B.

Consider the following:

()

where 𝔦 denotes sinθ_v, 𝔧 denotes

, 𝔨 denotes

, 𝔩 denotes

, 𝔪 denotes cos θ_v, 𝔫 denotes

, 𝔬 denotes

, 𝔭 denotes

, 𝔮 denotes sinh θ_v, 𝔯 denotes

, 𝔰 denotes

, 𝔱 denotes

, 𝔲 denotes cosh θ_v, 𝔳 denotes

, 𝔴 denotes

, 𝔵 denotes

, 𝔶 denotes −sinθ_v+1, 𝔷 denotes

, 𝕫 denotes

, 𝕪 denotes

, 𝕩 denotes −cos θ_v+1, 𝕨 denotes

, 𝕧 denotes

, 𝕦 denotes

, 𝕥 denotes −sinh θ_v+1, 𝔰 denotes

, 𝕣 denotes

, 𝕢 denotes

, 𝕡 denotes −cosh θ_v+1, 𝕠 denotes

, 𝕟 denotes

, and 𝕞 denotes

C.

Consider the following:

()

where 𝔸 denotes (δ1sin θ_N + ηcos θ_N), 𝔹 denotes (κsin θ_N + ψ1cos θ_N), ℂ denotes (δ1cos θ_N − ηsin θ_N), 𝔻 denotes (κcos θ_N − ψ1sin θ_N), 𝔼 denotes (δ2sinh θ_N + ηcosh θ_N), 𝔽 denotes (κsinh θ_N + ψ2cosh θ_N), 𝔾 denotes (δ2cosh θ_N + ηsinh θ_N), and ℍ denotes (κcosh θ_N + ψ2sinh θ_N).

References

1 Nagaya K., Transient response in flexure to general uni-directional loads of variable cross-section beam with concentrated tip inertias immersed in a fluid, Journal of Sound and Vibration. (1985) 99, no. 3, 361–378, 2-s2.0-0022421099.
10.1016/0022-460X(85)90374-8
Web of Science® Google Scholar
2 Nagaya K. and Hai Y., Seismic response of underwater members of variable cross section, Journal of Sound and Vibration. (1985) 103, no. 1, 119–138, 2-s2.0-0022421684.
10.1016/0022-460X(85)90251-2
Web of Science® Google Scholar
3 Chang J. Y. and Liu W. H., Some studies on the natural frequencies of immersed restrained column, Journal of Sound and Vibration. (1989) 130, no. 3, 516–524, 2-s2.0-0024964560.
10.1016/0022-460X(89)90075-8
Web of Science® Google Scholar
4 Uściłowska A. and Kołodziej J. A., Free vibration of immersed column carrying a tip mass, Journal of Sound and Vibration. (1998) 216, no. 1, 147–157, 2-s2.0-0039996698.
10.1006/jsvi.1998.1694
Web of Science® Google Scholar
5 Öz H. R., Natural frequencies of an immersed beam carrying a tip mass with rotatory inertia, Journal of Sound and Vibration. (2003) 266, no. 5, 1099–1108, 2-s2.0-0141741258, https://doi.org/10.1016/S0022%2D460X(03)00052%2DX.
10.1016/S0022-460X(03)00052-X
Web of Science® Google Scholar
6 Chan K. T. and Zhang J. Z., Free vibration of a cantilever tube partially filled with liquid, Journal of Sound and Vibration. (1995) 182, no. 2, 185–190, 2-s2.0-0001333105, https://doi.org/10.1006/jsvi.1995.0190.
10.1006/jsvi.1995.0190
Web of Science® Google Scholar
7 Amabili M., Vibrations of circular tubes and shells filled and partially immersed in dense fluids, Journal of Sound and Vibration. (1999) 221, no. 4, 567–585, 2-s2.0-0001413736.
10.1006/jsvi.1998.2050
Web of Science® Google Scholar
8 Wu J. S. and Chen C. T., An exact solution for the natural frequencies and mode shapes of an immersed elastically restrained wedge beam carrying an eccentric tip mass with mass moment of inertia, Journal of Sound and Vibration. (2005) 286, no. 3, 549–568, 2-s2.0-21444435095, https://doi.org/10.1016/j.jsv.2004.10.008.
10.1016/j.jsv.2004.10.008
Web of Science® Google Scholar
9 Wu J. S. and Hsu S. H., A unified approach for the free vibration analysis of an elastically supported immersed uniform beam carrying an eccentric tip mass with rotary inertia, Journal of Sound and Vibration. (2006) 291, no. 3–5, 1122–1147, 2-s2.0-31644431509, https://doi.org/10.1016/j.jsv.2005.07.032.
10.1016/j.jsv.2005.07.032
Web of Science® Google Scholar
10 Wu J. S. and Hsu S. H., The discrete methods for free vibration analyses of an immersed beam carrying an eccentric tip mass with rotary inertia, Ocean Engineering. (2007) 34, no. 1, 54–68, 2-s2.0-33751002622, https://doi.org/10.1016/j.oceaneng.2005.12.003.
10.1016/j.oceaneng.2005.12.003
Web of Science® Google Scholar
11 Lin H. Y., Dynamic analysis of a multi-span uniform beam carrying a number of various concentrated elements, Journal of Sound and Vibration. (2008) 309, no. 1-2, 262–275, 2-s2.0-35448988542, https://doi.org/10.1016/j.jsv.2007.07.015.
10.1016/j.jsv.2007.07.015
Web of Science® Google Scholar
12 Lin H. Y., On the natural frequencies and mode shapes of a multi-span and multi-step beam carrying a number of concentrated elements, Structural Engineering and Mechanics. (2008) 29, no. 5, 531–550, 2-s2.0-47549099802.
10.12989/sem.2008.29.5.531
Web of Science® Google Scholar
13 Lin H. Y., On the natural frequencies and mode shapes of a multispan Timoshenko beam carrying a number of various concentrated elements, Journal of Sound and Vibration. (2009) 319, no. 1-2, 593–605, 2-s2.0-56749138211, https://doi.org/10.1016/j.jsv.2008.05.022.
10.1016/j.jsv.2008.05.022
Web of Science® Google Scholar
14 Chakrabarti S. K. and Frampton R. E., Review of riser analysis techniques, Applied Ocean Research. (1982) 4, no. 2, 73–90, 2-s2.0-0020116590.
10.1016/S0141-1187(82)80002-3
Google Scholar

Citing Literature

All articles

Vibration of an Offshore Structure Having the Form of a Hollow Column Partially Filled with Multiple Fluids and Immersed in Water

Abstract

1. Introduction

2. Theoretical Model

2.1. Equation of Motion and Displacement Function

2.2. Coefficient Matrix [B_u] for an Intermediate Fluid Interface

2.3. Coefficient Matrix [B_v] for an Intermediate Applied Force

2.4. Coefficient Matrices [B₀] and [B_N] for the Two Ends of the Entire Beam

2.5. Determination of Natural Frequencies and Mode Shapes of the Beam

2.6. Determination of Forced Vibration Response of the Beam

3. Numerical Results and Discussions

3.1. Reliability of the Developed Computer Program

3.2. Natural Frequencies and Mode Shapes of the Immersed Hollow Beam Filled with Two Kinds of Fluids Carrying an Eccentric Tip Mass with Rotary Inertia, Translational and Rotational Spring Supports

3.3. Forced Vibration Responses of the Hollow Beam Filled with Two kinds of Fluids, Immersed in Water and Carrying an Eccentric Tip Mass

4. Conclusion

Appendices

A.

B.

C.

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Vibration of an Offshore Structure Having the Form of a Hollow Column Partially Filled with Multiple Fluids and Immersed in Water

Abstract

1. Introduction

2. Theoretical Model

2.1. Equation of Motion and Displacement Function

2.2. Coefficient Matrix [Bu] for an Intermediate Fluid Interface

2.3. Coefficient Matrix [Bv] for an Intermediate Applied Force

2.4. Coefficient Matrices [B0] and [BN] for the Two Ends of the Entire Beam

2.5. Determination of Natural Frequencies and Mode Shapes of the Beam

2.6. Determination of Forced Vibration Response of the Beam

3. Numerical Results and Discussions

3.1. Reliability of the Developed Computer Program

3.2. Natural Frequencies and Mode Shapes of the Immersed Hollow Beam Filled with Two Kinds of Fluids Carrying an Eccentric Tip Mass with Rotary Inertia, Translational and Rotational Spring Supports

3.3. Forced Vibration Responses of the Hollow Beam Filled with Two kinds of Fluids, Immersed in Water and Carrying an Eccentric Tip Mass

4. Conclusion

Appendices

A.

B.

C.

References

Citing Literature

Figures

References

Related

Information

2.2. Coefficient Matrix [B_u] for an Intermediate Fluid Interface

2.3. Coefficient Matrix [B_v] for an Intermediate Applied Force

2.4. Coefficient Matrices [B₀] and [B_N] for the Two Ends of the Entire Beam