Volume 2012, Issue 1 156095

Research Article

Open Access

Superconvergence Analysis of Finite Element Method for a Second-Type Variational Inequality

Dongyang Shi,

Dongyang Shi

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Search for more papers by this author

Hongbo Guan,

Hongbo Guan

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Department of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou 450002, China zzu.edu.cn

Search for more papers by this author

Xiaofei Guan,

Corresponding Author

Xiaofei Guan

[email protected]

Department of Mathematics, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author

Dongyang Shi,

Dongyang Shi

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Search for more papers by this author

Hongbo Guan,

Hongbo Guan

Department of Mathematics, Zhengzhou University, Zhengzhou 450001, China zzu.edu.cn

Department of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou 450002, China zzu.edu.cn

Search for more papers by this author

Xiaofei Guan,

Corresponding Author

Xiaofei Guan

[email protected]

Department of Mathematics, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author

First published: 26 November 2012

https://doi.org/10.1155/2012/156095

Citations: 1

Academic Editor: Song Cen

Share a link

Email
Wechat
Bluesky

Abstract

This paper studies the finite element (FE) approximation to a second-type variational inequality. The supe rclose and superconvergence results are obtained for conforming bilinear FE and nonconforming EQ^rot FE schemes under a reasonable regularity of the exact solution u ∈ H^5/2(Ω), which seem to be never discovered in the previous literature. The optimal L²-norm error estimate is also derived for EQ^rot FE. At last, some numerical results are provided to verify the theoretical analysis.

1. Introduction

Variational inequality (VI) theory has been playing an important role in the obstacle problem, contact problem, elasticity problem, and so on [1]. FE methods for solving VI problems have attracted more and more attentions. For example, as regards to the first type-VI case, the authors of [2] used piecewise quadratic FE to approximate the obstacle problem and suggested the error order between the FE solution and the exact solution should be O(h^3/2). The authors of [3] first obtained the error bound O(h^3/2−ε) (for any ε> 0) for the above FE when the obstacle vanished. Then through a detailed analysis, the authors of [4] obtained the same error bound as the ones of [3] under the hypothesis that the free boundary has finite length. Later, the authors of [5] obtained the same error bound as the ones of [3] for the same element without the hypothesis of finite length of the free boundary. Furthermore, [6] investigated the Wilson’s element approximation to the obstacle problem and derived the error bound with order O(h). The authors of [7] obtained the same error estimate with order O(h) on anisotropic meshes by making the full use of the bilinear part of the Wilson element, which relaxed the interpolation restriction and simplified the proofs of [5, 6]. Recently, the authors of [8] proposed a class of nonconforming FE methods for the parabolic obstacle VI problem with moving grids and obtained the optimal error estimates on anisotropic meshes. On the other hand, some studies [9–11] have been devoted to FE approximation to Signorini problem which arises in contact problems and obtained different error estimates under different assumptions. The authors of [12] derived the convergence result of O(h^3/4 | log h|^1/4) if the displacement field is of H² regularity and also showed that if stronger but reasonable regularity is available (u ∈ W^2,p, p > 2), the above result can be improved to optimal order O(h). The authors of [13] applied a class of Crouzeix-Raviart-type FEs to Signorini problem and obtained O(h) order estimate on anisotropic meshes. The authors of [14] used the bilinear FE to approximate the frictionless Signorini problem by virtue of the information on the contact zone and derived a superconvergence rate of O(h^3/2) when the exact solution u ∈ H^5/2(Ω). The authors of [15] presented the nonconforming Carey FE approximation to the problem of [14] and obtained the same convergence and superconvergence results are also obtained.

For the second type case, the authors of [16] proposed a Galerkin FE schemes for deriving a posteriori error estimates for a friction problem and a model flow of Bingham fluid. The authors of [17] considered the FE approximation to the plate contact problem and obtained some error estimates by employing the technique of mesh dependent norm.

In this paper, we will consider the following second type-VI problem [18, 19]:

()

where Ω ⊂ R² is a bounded convex polygonal domain; K^* is defined as follows:

()

in which Γ = ∂Ω, Γ_d ⊂ Γ and

. a(u, v) = ∫_Ω (∇u∇v + μuv)dx dy, μ is a positive constant,

, and

()

and g and k are positive constants. (1.1) may describe many practical engineering problems and attracts many scholars’ interests. For instance, the authors of [20] obtained the O(h^1/2−ε) error estimate of energy norm for linear FE; the authors of [21] got the O(h^1/2) error estimate in energy norm by improving the result of [20] for u ∈ H^3/2(Ω); the authors of [22] derived the optimal O(h²) error estimate of L² norm and O(h) error estimate of energy norm when u ∈ H²(Ω). But all the above studies mentioned above only paid attention to the convergence analysis for the conforming FE with no consideration on the superconvergence property, although it is surely an interesting and useful phenomenon in scientific computing of industrial problems [23].

In this paper, as a first attempt, we try to investigate the superconvergence of conforming and nonconforming FE schemes for problem (1.1) with a reasonable assumption of u ∈ H^5/2(Ω). The rest of this paper is organized as follows. In the next section, we give the equivalent form of (1.1) and the conforming bilinear FE (see [14]) approximation of (1.1). Moreover, superclose result of O(h^3/2) is derived under the broken energy norm. In Section 3, the nonconforming EQ^rot FE (see [26]) approximation is used, and the same superclose result is obtained under the energy norm; the optimal error estimate of L²-norm is also derived when u ∈ H²(Ω). In Section 4, we construct a postprocessing interpolation operator to obtain the superconvergence properties. In Section 5, we present some numerical results to verify the theoretical analysis.

2. The Equivalent Form and Conforming FE Scheme

It has been shown in [21, 22] that (1.1) is equivalent to

()

and (2.1) has the unique solution u in K^*. It can be verified that φ(t) satisfies the following two properties: for all a, b ∈ R¹,

()

Let T_h be a rectangular partition with a maximum size h in (x, y) plane, K ∈ T_h a general element;

and

are the conforming bilinear FE space and the nonconforming EQ^rot FE space. We denote by

and

the associated interpolation operators on

and

, respectively. In the meantime, we denote

by a convex set associated with K^* in

(i = 1, 2) as follows:

()

where F is an edge of K. The following two lemmas will play an important role in the FE analysis, which can be found in [14, 24], respectively.

Lemma 2.1. For all u ∈ H²(Ω), F ⊂ ∂K, there holds .

Lemma 2.2. Let u ∈ H^5/2(Ω), then for , there holds

()

where

The corresponding conforming FE approximation version of (2.1) reads as

()

Theorem 2.3. Let u ∈ H^5/2(Ω) be the exact solution of (1.1) and the bilinear FE solution of (2.6), then there holds

()

here and later, c is a generic positive constant, which is independent of h, K, and u.

Proof. Subtracting (2.1) from (2.6), then taking v = v_h in it, one can get

()

Let

and

. Taking v_h = ξ in the above equation, there yields

()

By the definition of a(v, v), we have

()

Noticing (2.3), we have

; thus

()

in which

From (2.2) and Lemma 2.1, I₁ can be estimated as

()

Applying the interpolation theory and Lemma 2.2, we get

()

The desired result follows directly from the combination of (2.12) and (2.13).

3. The Nonconforming FE Scheme

The corresponding nonconforming FE approximation scheme of (2.1) reads as

()

where a_h(u, v) = ∑ _K∫_K (∇u∇v + μuv)dx dy.

First, we introduce the following Lemma 3.1, which can be found in [25].

Lemma 3.1 (see [25].)If , one has

()

By using the similar technique in [26], one now states and proves the following important conclusion.

Lemma 3.2. For all , there holds

()

where

Proof. Let Z₁ = (x₀ − h_x, y₀ − h_y), Z₂ = (x₀ + h_x, y₀ − h_y), Z₃ = (x₀ + h_x, y₀ + h_y), and Z₄ = (x₀ − h_x, y₀ + h_y) be the four vertices of K, . We define operators P₀ and P_0i as

()

respectively, where |K| and |F_i| denote the measures of K and F_i, respectively.

It can be checked that

()

By the definition of P₀₁, we get

()

Noticing that equals and ∂v_h/∂x is only dependent on x, we can derive that

()

Similarly, M₂ + M₄ ≤ ch^3/2 | u|_5/2,K | v_h|_1,K. By using the same technique as [14, 15], M can be estimated as

()

Thus the desired result follows.

Theorem 3.3. Let u ∈ H^5/2(Ω) be the exact solution of (1.1) and the nonconforming FE solution of (3.1). Then one has

()

Proof. Subtracting (2.1) from (3.1) gives

()

For convenience, we still denote and . Taking in (3.10) yields

()

By Lemma 3.1, we can derive that

()

Noticing Lemma 3.2 and using the analysis technique of Theorem 2.3, one can immediately get the desired result.

Remark 3.4. As a by-product, if we assume u ∈ H²(Ω) instead of u ∈ H^5/2(Ω), the consistency error can be estimated as

()

which can be found in [26]. Then we can derive the following optimal error estimate:

()

Now we start to give the L²-norm estimate through a duality argument.

Theorem 3.5. Let u ∈ K²(Ω) and be the solutions of (1.1) and (3.1), respectively, there holds

()

Proof. Let ω ∈ H²(Ω) be the solution of the following auxiliary elliptic problem:

()

in which β(x) = (φ(u) − φ(u_h))/(u − u_h), then

()

By (3.16) and Lemma 3.1, we can derive that

()

where

. These three terms can be estimated one by one as follows. By (3.14), (3.17), and the interpolation theory, J₁ can be estimated as

()

By the trace theorem, (3.17), and Lemma 2.1, one gets

()

By (3.13), (3.14), and (3.17), we have

()

The desired result follows the combination of the above estimates of J₁, J₂, and J₃.

Remark 3.6. As to the L²-norm error estimate of bilinear FE scheme, the readers may refer to [21, 22].

4. The Global Superconvergence Result

In order to obtain the global superconvergence, we combine the four neighbouring elements K₁, K₂, K₃, K₄ ∈ T_h into one new rectangular element K₀, whose four edges are L₁, L₂, L₃, and L₄. T_2h represents the corresponding new partition. For the conforming FE scheme, we construct the postprocessing operator

as follows:

()

in which Z_j is the four vertices and four mid point of edges of K₀. For the nonconforming FE scheme, we construct the postprocessing

operator as

()

It is easy to validate that the interpolation operator is well posed and has the following properties [23]:

()

Theorem 4.1. If u ∈ H^5/2(Ω) is the exact solution of (1.1), u_h is the conforming or nonconforming FE solution. The following superconvergence result

()

holds.

Proof. By (4.3), one gets

()

Noticing , the proof is completed.

5. Numerical Results

In this section, we will present an example to confirm the correctness of our theoretical analysis. In (1.1), we choose Ω = [0,1]×[0,1] with boundary . The right hand term f = 1. Since there may be no exact solution to the above problem, we use the conforming FE solution on a sufficient refined mesh h = 1/256 as the reference solution. Then we compare the conforming and nonconforming FE solutions (see Figure 1) on the coarser meshes (h = 1/2, 1/4, 1/8, 1/16, 1/32, 1/64) with the reference one in Tables 1 and 2.

Table 1. The error estimates for conforming FE scheme.

h	1/2	1/4	1/8	1/16	1/32	1/64
	2.1780E−02	6.6596E−03	1.8851E−03	5.1760E−04	1.3861E−04	3.5405E−05
order	/	1.8084	1.8796	1.9084	1.9324	1.9786
	5.3923E−03	1.5926E−03	4.1215E−04	1.0371E−04	2.5691E−05	6.1214E−06
order	/	1.8401	1.9657	1.9935	2.0092	2.0486

Table 2. The error estimates for nonconforming FE scheme.

h	1/2	1/4	1/8	1/16	1/32	1/64
	1.1264E−01	4.6572E−02	1.8679E−02	8.0004E−03	3.1977E−03	1.3906E−03
order	/	1.5552	1.5790	1.5280	1.5817	1.5164
	8.1523E−02	3.1059E−02	1.0260E−02	3.1725E−03	9.4359E−04	2.7340E−04
order	/	1.6201	1.7399	1.7983	1.8336	1.8578
	1.0995E−02	2.7109E−03	6.4263E−04	1.5941E−04	3.9258E−05	9.3430E−06
order	/	2.0139	2.0539	2.0078	2.0151	2.0498

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The conforming FE solution (a) and the nonconforming FE solution (b) on the 64 × 64 mesh.

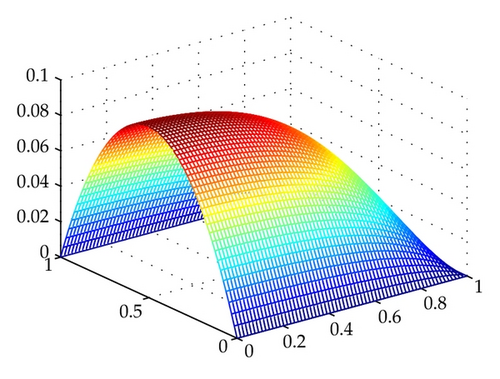
From the above tables, we can see that the conforming and nonconforming FE solutions both converge. At the same time, the superconvergence results in our experiments are a little better than the theoretical ones. We may explain this phenomenon with some special properties of this nonconforming FE that we have not discovered.

Acknowledgments

The first author was supported by the National Natural Science Foundation of China under Grant 10971203. The third author was supported by the National Natural Science Foundation of China under Grant 11126132. The authors would like to thank the referees for their valuable suggestions and corrections, which contribute significantly to the improvement of the paper.

References

1 Hartman P. and Stampacchia G., On some non-linear elliptic differential-functional equations, Acta Mathematica. (1966) 115, 271–310, 0206537, https://doi.org/10.1007/BF02392210, ZBL0142.38102.
10.1007/BF02392210
Web of Science® Google Scholar
2 Strang G., The finite element method—linear and nonlinear applications, Proceedings of the International Congress of Mathematicians, 1974, Vancouver, Canada, 429–435, 0423842.
Google Scholar
3 Brezzi F. and Sacchi G., A finite element approximation of a variational inequality related to hydraulics, Calcolo. (1976) 13, no. 3, 257–273, 0520171, ZBL0353.76068.
10.1007/BF02575934
Google Scholar
4 Brezzi F., Hager W. W., and Raviart P.-A., Error estimates for the finite element solution of variational inequalities, Numerische Mathematik. (1977) 28, no. 4, 431–443, 0448949, https://doi.org/10.1007/BF01404345, ZBL0369.65030.
10.1007/BF01404345
Web of Science® Google Scholar
5 Wang L., On the quadratic finite element approximation to the obstacle problem, Numerische Mathematik. (2002) 92, no. 4, 771–778, https://doi.org/10.1007/s002110100368, 1935809, ZBL1049.65062.
10.1007/s002110100368
Web of Science® Google Scholar
6 Wang L., On the error estimate of nonconforming finite element approximation to the obstacle problem, Journal of Computational Mathematics. (2003) 21, no. 4, 481–490, 1990208, ZBL1053.65049.
Web of Science® Google Scholar
7 Shi D. Y. and Wang C. X., Anisotropic nonconforming finite element approximation to variational inequality problems with displacement obstacle, Chinese Journal of Engineering Mathematics. (2006) 23, no. 3, 399–406, 2252283, ZBL1115.65340.
Google Scholar
8 Shi D. and Guan H., A class of Crouzeix-Raviart type nonconforming finite element methods for parabolic variational inequality problem with moving grid on anisotropic meshes, Hokkaido Mathematical Journal. (2007) 36, no. 4, 687–709, 2378286, ZBL1181.65100.
10.14492/hokmj/1272848028
Google Scholar
9 Ben Belgacem F., Numerical simulation of some variational inequalities arisen from unilateral contact problems by the finite element methods, SIAM Journal on Numerical Analysis. (2000) 37, no. 4, 1198–1216, https://doi.org/10.1137/S0036142998347966, 1756422, ZBL0974.74055.
10.1137/S0036142998347966
Web of Science® Google Scholar
10 Belhachmi Z. and Belgacem F. B., Quadratic finite element approximation of the Signorini problem, Mathematics of Computation. (2003) 72, no. 241, 83–104, https://doi.org/10.1090/S0025%2D5718%2D01%2D01413%2D2, 1933319, ZBL1112.74446.
10.1090/S0025-5718-01-01413-2
Web of Science® Google Scholar
11 Ben Belgacem F. and Renard Y., Hybrid finite element methods for the Signorini problem, Mathematics of Computation. (2003) 72, no. 243, 1117–1145, https://doi.org/10.1090/S0025%2D5718%2D03%2D01490%2DX, 1972730, ZBL1023.74043.
10.1090/S0025-5718-03-01490-X
Web of Science® Google Scholar
12 Hua D. and Wang L., The nonconforming finite element method for Signorini problem, Journal of Computational Mathematics. (2007) 25, no. 1, 67–80, 2292428, ZBL1142.65369.
Web of Science® Google Scholar
13 Shi D. Y., Mao S. P., and Chen S. C., A class of anisotropic Crouzeix-Raviart type finite element approximations to the Signorini variational inequality problem, Chinese Journal of Numerical Mathematics and Applications. (2005) 27, no. 1, 69–78, 2148218.
Google Scholar
14 Li M., Lin Q., and Zhang S., Superconvergence of finite element method for the Signorini problem, Journal of Computational and Applied Mathematics. (2008) 222, no. 2, 284–292, https://doi.org/10.1016/j.cam.2007.10.058, 2474630, ZBL1148.74044.
10.1016/j.cam.2007.10.058
Web of Science® Google Scholar
15 Shi D., Ren J., and Gong W., Convergence and superconvergence analysis of a nonconforming finite element method for solving the Signorini problem, Nonlinear Analysis A. (2012) 75, no. 8, 3493–3502, https://doi.org/10.1016/j.na.2012.01.007, 2901332.
10.1016/j.na.2012.01.007
Web of Science® Google Scholar
16 Hage D., Klein N., and Suttmeier F. T., Adaptive finite elements for a certain class of variational inequalities of second kind, Calcolo. (2011) 48, no. 4, 293–305, https://doi.org/10.1007/s10092%2D011%2D0040%2D2, 2855533, ZBL1239.65042.
10.1007/s10092-011-0040-2
Web of Science® Google Scholar
17 An R. and Li K. T., Mixed finite element approximation for the plate contact problem, Acta Mathematica Scientia. (2010) 30, no. 3, 666–676, 2682940, ZBL1240.74014.
CAS Google Scholar
18 Zhou S., Variational Inequalities and Its FEM, 1994, Hunan University press, Changsha, China.
Google Scholar
19 Kikuchi N. and Oden J. T., Contact Problem in Elasticity, 1988, 8, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, Pa, USA, SIAM Studies in Applied Mathematics, 961258.
10.1137/1.9781611970845
Google Scholar
20 Glowinski R., Lions J.-L., and Trémolières R., Numerical Analysis of Variational Inequalities, 1981, 8, North-Holland Publishing, Amsterdam, The Netherlands, Studies in Mathematics and its Applications, 635927.
Google Scholar
21 Wang L. H., The finite element approximation to a second type variational inequality, Mathematica Numerica Sinica. (2000) 22, no. 3, 339–344, 1797954.
Google Scholar
22 Zhang T. and Li C. J., Finite element approximation to the second type variational inequality, Mathematica Numerica Sinica. (2003) 25, no. 3, 257–264, 2001159.
Web of Science® Google Scholar
23 Lin Q. and Lin J., Finite Element Methods: Accuracy and Improvement, 2006, Science Press, Beijing, China.
Google Scholar
24 Brenner S. C. and Scott L. R., The Mathematical Theory of Finite Element Methods, 1994, 15, Springer, Berlin, Germany, 1278258.
10.1007/978-1-4757-4338-8
Google Scholar
25 Shi D. Y. and Guan H. B., A kind of full-discrete nonconforming finite element method for the parabolic variational inequality, Acta Mathematicae Applicatae Sinica. (2008) 31, no. 1, 90–96, 2449850.
Google Scholar
26 Shi D., Mao S., and Chen S., An anisotropic nonconforming finite element with some superconvergence results, Journal of Computational Mathematics. (2005) 23, no. 3, 261–274, 2133919, ZBL1074.65133.
Web of Science® Google Scholar

Citing Literature

All articles

Superconvergence Analysis of Finite Element Method for a Second-Type Variational Inequality

Abstract

1. Introduction

2. The Equivalent Form and Conforming FE Scheme

3. The Nonconforming FE Scheme

4. The Global Superconvergence Result

5. Numerical Results

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Superconvergence Analysis of Finite Element Method for a Second-Type Variational Inequality

Abstract

1. Introduction

2. The Equivalent Form and Conforming FE Scheme

3. The Nonconforming FE Scheme

4. The Global Superconvergence Result

5. Numerical Results

Acknowledgments

References

Citing Literature

Figures

References

Related

Information