Convergence and Stability in Collocation Methods of Equation u′(t) = au(t) + bu([t])
Abstract
This paper is concerned with the convergence, global superconvergence, local superconvergence, and stability of collocation methods for u′(t) = au(t) + bu([t]). The optimal convergence order and superconvergence order are obtained, and the stability regions for the collocation methods are determined. The conditions that the analytic stability region is contained in the numerical stability region are obtained, and some numerical experiments are given.
1. Introduction
There are some authors who have considered the stability of numerical solutions for this kind of equations (see [6–8]). Though (1.1) is a delay differential equation (see [9–11]), the delay function t − [t] is discontinuous. In [12], the convergence and superconvergence of collocation methods for a differential equation with piecewise linear delays is concerned.
Definition 1.1 (see Wiener [5].)A solution of (1.1) on [0, ∞) is a function u(t) that satisfies the following conditions.
- (1)
u(t) is continuous on [0, ∞).
- (2)
The derivative u′(t) exists at each point t ∈ [0, ∞), with the possible exception of the point [t]∈[0, ∞), where one-sided derivatives exist.
- (3)
(1.1) is satisfied on each interval [k, k + 1)⊂[0, ∞) with integral endpoints.
2. Existence and Uniqueness of Collocation Methods
So we can obtain the following theorem.
Theorem 2.1. Assume that the given functions in (1.1) satisfy a, b ∈ ℝ, K ∈ C(D), where D : = {(t, s) : 0 ≤ s ≤ t ≤ T}. Then there exists an so that for the mesh Ih with mesh diameter h > 0 satisfying , and each of the linear algebraic systems (2.10) has a unique solution Yn ∈ ℝm. Hence the collocation of (2.4) defines a unique collocation solution for the initial-value problem (1.1), and its representation on the subinterval [tn, tn+1] is given by (2.11).
3. Global Convergence Results
In the following, unless otherwise specified, the derivatives of u and uh denote the left derivatives.
Theorem 3.1. Assume the following:
- (1)
the given functions in (1.1) satisfy a, b ∈ ℝ, K ∈ Cm(D);
- (2)
is the collocation solution to (1.1) defined by (2.10) and (2.11) with .
Proof. The collocation error eh : = u − uh satisfies the equation
Denote
Equation (3.14) now leads to the estimate
4. Global Superconvergence Results
Theorem 4.1. Assume that the assumptions (2) of Theorem 3.1 hold, and let (1) be replaced by a, b ∈ Cd(I) and K ∈ Cd(D), with d ≥ m + 1. If the m collocation parameters {ci} are subject to the orthogonality condition
Proof. Let
It following from (4.3) that the collocation error eh = u − uh satisfies the equation
We assume for t ∈ [k − 1, k]
5. The Local Superconvergence Results on Ih
Theorem 5.1. Assume the following:
- (a)
a, b ∈ Cm+κ(I) and K ∈ Cm+κ(D), for some κ with 1 ≤ κ ≤ m and value as specified in (b) below,
- (b)
The m distinct collocation parameters {ci} are chosen so that the general orthogonality condition
()
Then, for all meshes Ih with , the collocation solution corresponding to the collocation points Xh based on these {ci} satisfies
6. Numerical Stability
Definition 6.1 (see [6].)Process (2.11) for (1.1) is called asymptotically stable at (a, b) if and only if for all m ≥ M and h = 1/m.
- (i)
(I − xA) is invertible.
- (ii)
for any given ui (1 ≤ i ≤ m) relation (6.4) defines Uk (k = 1,2, …) that satisfy Uk → 0 for k → ∞.
Definition 6.2 (see [6].)The set of all pairs (a, b) at which the process (2.11) for (1.1) is asymptotically stable is called asymptotical stability region denoted by S.
Theorem 6.3 (see [6].)Suppose that the collocation method is A0-stable and the stability function is given by the (r, s)-Padé approximation to the exponential ex. Then H1⊆S if and only if r is even.
Theorem 6.4 (see [6].)Suppose that the stability function of the collocation method is given by the (r, s)-Padé approximation to the exponential ez. Then H2⊆S if and only if s is even.
Theorem 6.5 (see [6].)For all the collocation methods, we have H0⊆S.
Using the above theorems we can formulate the following result.
Theorem 6.6 (see [6].)Suppose that the collocation method is A0-stable and the stability function is given by the (r, s)-Padé approximation to the exponential ex. Then H0⊆S and H⊆S if and only if both r and s are even,
Corollary 6.7. For the A-stable higher order collocation methods, it is easy to see from Theorem 6.6.
- (i)
For the ν-stage Gauss-Legendre method, H⊆S if and only if ν is even.
- (ii)
For the ν-stage Lobatto IIIA method, H⊆S if and only if ν is old.
- (iii)
For the ν-stage Radau IIA method, H1⊆S if and only if ν is old and H2⊆S if and only if ν is even.
7. Numerical Experiments
For illustrating the convergence and superconvergence orders in this paper, we choose m = 2 and m = 3 and use the Gauss collocation parameters: , , the Radau IIA collocation parameters: c1 = 1/3, c2 = 1, the Lobatto IIIA collocation parameters: c1 = 0, c2 = 1, and three sets of random collocation parameters: c1 = 1/4, c2 = 1/2; c1 = 1/3, c2 = 2/3; c1 = 2/3, c2 = 1, respectively, for m = 2; and we use the Gauss collocation parameters: , c2 = 1/2, and , the Radau IIA collocation parameters: , , and c3 = 1, the Lobatto IIIA collocation parameters: c1 = 0, c2 = 1/2, and c3 = 1, and three sets of random collocation parameters: c1 = 1/3, c2 = 1/2, c3 = 2/3; c1 = 1/4, c2 = 1/3, c3 = 1/2; c1 = 1/2, c2 = 2/3, c3 = 1, respectively, for m = 3. In Tables 1, 2, 3, and 4 we list the absolute values of the absolute errors of ut = 10 for the six collocation parameters and for m = 2 and m = 3, respectively, and the ratios of the absolute values of the errors of N = 100 over that of N = 200.
| N | Gauss | Radau IIA | Lobatto IIIA | (1/4, 1/2) | (1/3, 2/3) | (2/3, 1) |
|---|---|---|---|---|---|---|
| 21 | 1.2551e − 03 | 3.1476e − 04 | 1.3124e − 03 | 2.9655e + 02 | 1.3113e − 03 | 9.3953e − 06 |
| 22 | 4.5928e − 06 | 1.4601e − 06 | 8.5094e − 04 | 1.2874e − 03 | 6.4778e − 05 | 8.1731e − 10 |
| 23 | 2.4209e − 10 | 7.8934e − 11 | 8.1731e − 10 | 8.5023e − 07 | 1.0324e − 08 | 9.3978e − 10 |
| 24 | 6.1162e − 12 | 2.8697e − 11 | 7.7079e − 11 | 5.7012e − 10 | 1.3715e − 10 | 1.8633e − 10 |
| 25 | 3.4588e − 13 | 4.5808e − 12 | 3.9746e − 11 | 4.1164e − 11 | 2.0163e − 11 | 4.3362e − 11 |
| 26 | 2.1210e − 14 | 6.2301e − 13 | 1.2117e − 11 | 7.6587e − 12 | 4.4835e − 12 | 1.1275e − 11 |
| Ratio | 1.6307e + 01 | 7.3526e + 00 | 3.2802e + 00 | 5.3747e + 00 | 4.4973e + 00 | 3.8460e + 00 |
| N | Gauss | Radau IIA | Lobatto IIIA | (1/3, 1/2, 2/3) | (1/4, 1/3, 1/2) | (1/2, 2/3, 1) |
|---|---|---|---|---|---|---|
| 21 | 3.1476e − 04 | 9.9709e − 05 | 1.2551e − 03 | 1.2301e − 03 | 4.9431e + 04 | 4.8903e − 06 |
| 22 | 3.2248e − 11 | 1.6050e − 08 | 4.5928e − 06 | 2.6790e − 06 | 9.5944e − 04 | 3.2687e − 09 |
| 23 | 4.7508e − 12 | 2.0843e − 11 | 2.4209e − 10 | 6.7725e − 11 | 7.9577e − 11 | 1.1031e − 10 |
| 24 | 6.3943e − 14 | 5.8750e − 13 | 6.1162e − 12 | 6.7093e − 12 | 2.9944e − 11 | 1.6213e − 11 |
| 25 | 9.5085e − 16 | 1.9290e − 14 | 3.4588e − 13 | 4.1702e − 13 | 3.1783e − 12 | 2.5836e − 12 |
| 26 | 1.0192e − 17 | 6.3187e − 16 | 2.1210e − 14 | 2.5846e − 14 | 3.3739e − 13 | 3.7792e − 13 |
| Ratio | 9.3298e + 01 | 3.0528e + 01 | 1.6307e + 01 | 1.6135e + 01 | 9.4201 | 6.8363e + 00 |
| N | Gauss | Radau IIA | Lobatto IIIA | (1/4, 1/2) | (1/3, 2/3) | (2/3, 1) |
|---|---|---|---|---|---|---|
| 21 | 9.0789e − 01 | 9.1680e − 01 | 9.1647e − 01 | 9.0070e − 01 | 9.1460e − 01 | 9.1700e − 01 |
| 22 | 2.3033e − 01 | 8.6133e − 01 | 4.2429e − 01 | 5.4055e − 01 | 7.4023e − 01 | 9.1661e − 01 |
| 23 | 8.9360e − 03 | 1.2191e − 01 | 8.3085e − 02 | 1.3822e − 01 | 1.5563e − 01 | 7.6499e − 01 |
| 24 | 5.0981e − 04 | 9.9479e − 03 | 5.9089e − 02 | 3.4017e − 02 | 2.8752e − 02 | 1.5140e − 01 |
| 25 | 3.1272e − 05 | 1.0927e − 03 | 1.8134e − 02 | 8.7800e − 03 | 6.5674e − 03 | 2.5303e − 02 |
| 26 | 1.9458e − 06 | 1.2993e − 04 | 4.7169e − 03 | 2.2713e − 03 | 1.6041e − 03 | 5.3924e − 03 |
| Ratio | 1.6071e + 01 | 8.4098e + 00 | 3.8445e + 00 | 3.8656e + 00 | 4.0940e + 00 | 4.6924e + 00 |
| N | Gauss | Radau IIA | Lobatto IIIA | (1/3, 1/2, 2/3) | (1/4, 1/3, 1/2) | (1/2, 2/3, 1) |
|---|---|---|---|---|---|---|
| 21 | 4.8459e − 02 | 9.0087e − 01 | 9.0789e − 01 | 9.0508e − 01 | 7.4280e − 02 | 9.1693e − 01 |
| 22 | 7.0515e − 03 | 5.0901e − 02 | 2.3033e − 01 | 8.2874e − 02 | 2.5303e − 02 | 8.3086e − 02 |
| 23 | 9.4311e − 05 | 1.3131e − 03 | 8.9360e − 03 | 9.9825e − 03 | 1.2122e − 02 | 6.3787e − 02 |
| 24 | 1.4090e − 06 | 3.5203e − 05 | 5.0981e − 04 | 6.1535e − 04 | 2.2659e − 03 | 7.4707e − 03 |
| 25 | 2.1766e − 08 | 1.0294e − 06 | 3.1272e − 05 | 3.8124e − 05 | 3.4308e − 04 | 7.9289e − 04 |
| 26 | 3.3592e − 10 | 3.1217e − 08 | 1.9458e − 06 | 2.3768e − 06 | 4.7157e − 05 | 9.0681e − 05 |
| Ratio | 6.4794e + 01 | 3.2977e + 01 | 1.6071e + 01 | 1.6040e + 01 | 7.2752e + 00 | 8.7437e + 00 |
From the above tables, we can see that the convergence orders are consistent with our theoretical analysis.
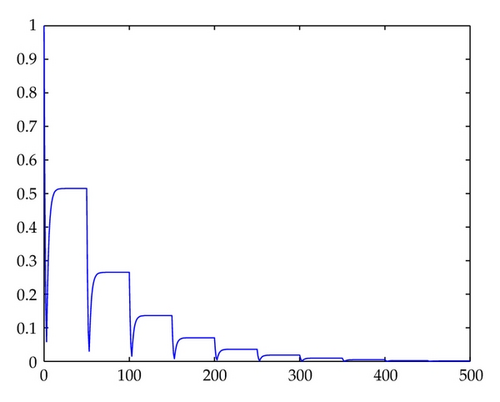
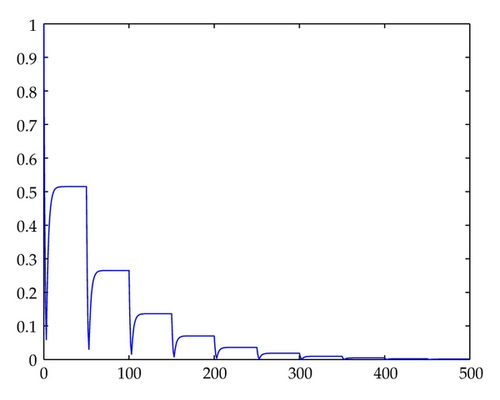
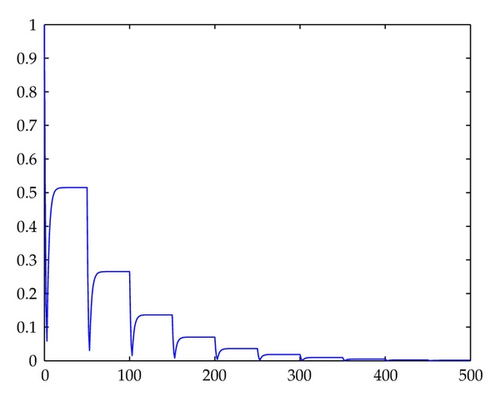
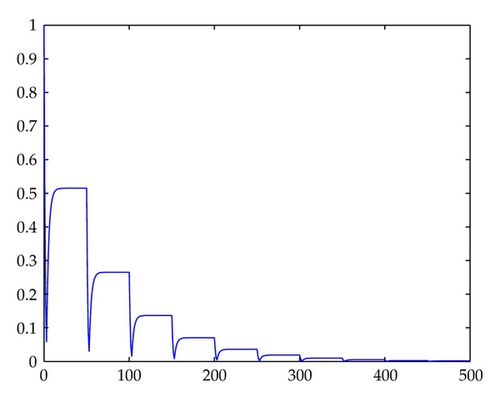
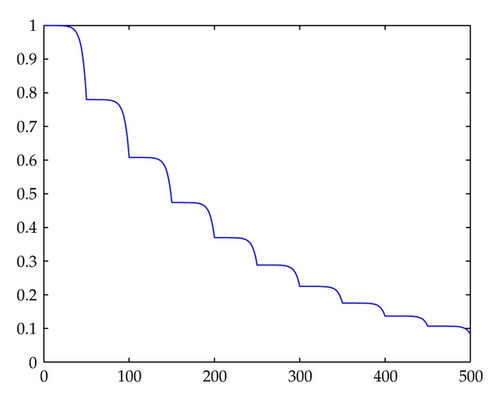
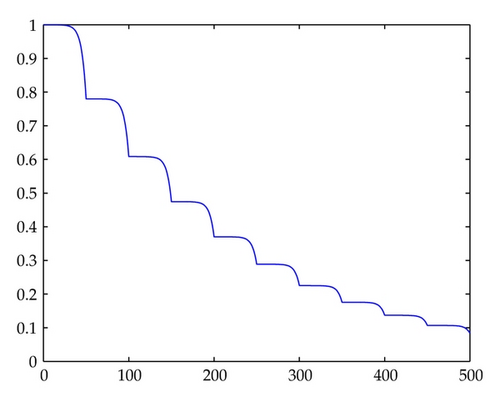
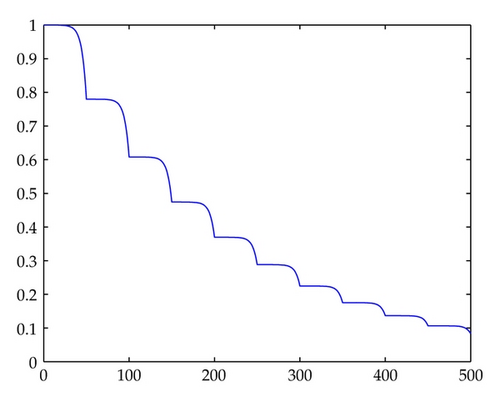
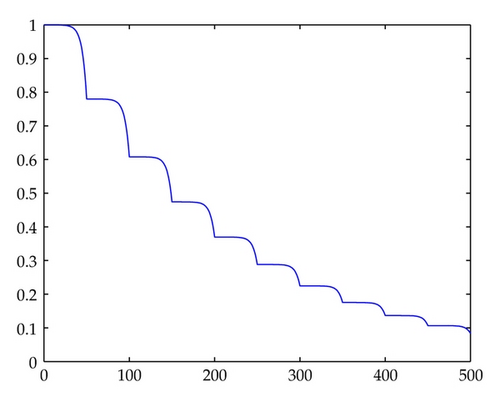
In Figures 1, 2, 3, 4, 5, 6, 7, and 8, we draw the absolute values of the numerical solution of collocation methods. It is easy to see that the numerical solution is asymptotically stable.
Acknowledgments
This work is supported by the Research Fund of the Heilongjiang Provincial Education Department (no. 11551363, no. 12511414), the National Nature Science Foundation of China (no. 11101130).




