Volume 2012, Issue 1 106830

Research Article

Open Access

Lag Synchronization of Coupled Multidelay Systems

Luo Qun

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Peng Hai-Peng,

Corresponding Author

Peng Hai-Peng

[email protected]

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Xu Ling-Yu,

Xu Ling-Yu

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Yang Yi Xian,

Yang Yi Xian

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Luo Qun,

Luo Qun

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Peng Hai-Peng,

Corresponding Author

Peng Hai-Peng

[email protected]

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Xu Ling-Yu,

Xu Ling-Yu

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

Yang Yi Xian,

Yang Yi Xian

Information Security Center, Beijing University of Posts and Telecommunications, P.O. Box 145, Beijing 100876, China bupt.edu.cn

Search for more papers by this author

First published: 28 June 2012

https://doi.org/10.1155/2012/106830

Citations: 3

Academic Editor: Mohamed A. Zohdy

Share a link

Email
Wechat
Bluesky

Abstract

Chaos synchronization is an active topic, and its possible applications have been studied extensively. In this paper we present an improved method for lag synchronization of chaotic systems with coupled multidelay. The Lyapunov theory is used to consider the sufficient condition for synchronization. The specific examples will demonstrate and verify the effectiveness of the proposed approach.

1. Introduction

Since synchronization of chaotic systems was first realized by Fujisaka and Yamada [1] and Pecora and Carroll [2], chaos synchronization has received increasing interest and has become an active research topic. Currently its possible applications in various fields are in great interest, for example, applications to control theory [3], telecommunications [4–7], biology [8, 9], lasers [10, 11], secure communications [12], and so on.

Roughly speaking, chaotic communication schemes rely on the synchronization technique: the information signal is mixed at the master, and a driving signal is then generated and is sent to the slave; as a result, their chaotic trajectories remain in step with each other during temporal evolution. Besides identical synchronization [13], several new types of chaos synchronization of coupled oscillators have occurred, that is, generalized synchronization [12], phase synchronization [14], lag synchronization [15], anticipation synchronization [16], and projective synchronization [17].

Lag synchronization can be realized when the strength of the coupling between phase-synchronized oscillators is increased. There, the driving signal is constituted by the sum of multiple nonlinear transformations of delayed state variable [18]. Master and slave′s formulas are in the form of single delay [19, 20] and multidelay [21–23]. From the application point of view, this new multidelay synchronization, different from conventional synchronization without lag, offers a significant advantage in terms of security of communication. Since the constructed state variable of the master system with lag becomes more complex than that of the conventional system, multilag systems achieve high security. Intruders cannot reconstruct the attractors of driving signal by using conventional reconstruction methods [24, 25] so as not to decipher the transferred message.

In the present paper, we proposed a systematic and rigorous scheme for lag synchronization of coupled multidelay systems based on the Lyapunov stability theory. Furthermore, the zero solution of lag synchronization differential equation is globally asymptotically stable. The effectiveness of the proposed scheme is confirmed by the numerical simulation of specific example.

2. The Schemes of Lag Synchronization

2.1. The Proposed Lag Synchronization Model

Lag synchronization was first investigated by Rosenblum [15], and it can be considered that the state variable of the slave is delayed by the positive time lag τ_d in comparison with that of the master while their amplitudes follow each other, that is, lim _t→∞|y(t) − x(t − τ_d)| = 0.

We consider the following model of lag synchronization.

Master:

(2.1)

Driving signal:

(2.2)

Slave:

(2.3)

where coefficients α, m_i, k_i, n_i, α_i, β_i, γ_i, W ∈ ℜ, and P, Q, R are positive integers. State variables x, y ∈ ℜ, and f_i(·), g_i(·), h_i(·) ∈ ℜ → ℜ are three continuous nonlinear functions. The driving signal DS(t) in (2.2) is constituted by the sum of multiple nonlinear transformations of delayed state variable;

is added with Wx(t − τ_d). The polynomial −Wy(t) is added to the right side of

, forming the slave equation which is shown as (2.3).

2.2. Proof for the Lag Synchronization Model

The desired synchronization manifold is expressed by the following relation y(t) → x(t − τ_d) as t → ∞, where τ_d is a lag time.

We choose suitable DS(t) to satisfy e(t) = y(t) − x(t − τ_d) → 0 as t → ∞.

Assumption 2.1. Q = P + R − I, I < min {P, Q, R} where I is integer. When i = 1, …, I, f_i ≡ g_i ≡ h_i,

(2.4)

Assumption 2.2. When j = 1, …, (P − I), g_I+j ≡ f_I+j,

(2.5)

When j = 1, …, (R − I), g_P+j ≡ h_I+j,

(2.6)

Assumption 2.3. Nonlinearity f_i (i = 1, …, I) satisfies Lipshitz condition; that is, there exists a positive constant L for all time variables a and b, such that |f_i(a + b) − f_i(a)| ≤ L|b| (i = 1, …, I).

Here we give the sufficient condition for system synchronization.

Theorem 2.4. If the system (2.1), (2.2), and (2.3) satisfies Assumptions 2.1, 2.2, and 2.3 and if

(2.7)

then lim _t→∞[y(t) − x(t − τ_d)] = 0.

Proof. The dynamics of synchronization error is

(2.8)

By applying Assumption 2.1, (2.8) can be rewritten as

(2.9)

By applying Assumption 2.2, if Q − I = (P − I) + (R − I) and y(t − γ_i) = x(t − γ_i − τ_d) + e(t − γ_i), we have

(2.10)

where e(t − γ_I+j) = 0 as well as synchronization established, in fact, e(t − γ_I+j) reduces during establishing the synchronization regime.

From (2.10) and (2.9) we get

(2.11)

Define a Lyapunov function [26] as

(2.12)

Then, we obtain

(2.13)

Here, we have

(2.14)

According to Assumption 2.1, we have

(2.15)

In our model, can be rewritten as (1/2)Ie²(t). By Assumption 2.3, we have

(2.16)

According to 2xy ≤ x² + y², where x, y ∈ ℜ, we get

(2.17)

Finally, we obtain

(2.18)

The proof is completed.

Note 1. The advantages of our lag synchronization model are as follows.

(1)
The nonlinear function f(·) satisfies |f(a + b) − f(a)| ≤ L|b|, so the zero solution of lag synchronization error system is globally asymptotically stable. The condition for synchronization is easy to be realized.
(2)
We can choose nonlinear function in many ways, and f_i, g_i, h_i vary as i changes. Moreover, the format of function can be different even if i is the same value.
(3)
In order to enhance the complexity of the system, P, Q, R can be different positive integers, and the number of multiple time delays can be chosen as many values.

3. Numerical Simulations

The following example will demonstrate synchronization between systems with multidelay. Functions of systems are chosen from the set of {sin u, u/(1 + u⁸), u/(1 + u¹⁰)}. Let us consider synchronization model with the master′s and slave′s equations defined as.

Master:

(3.1)

Slave:

(3.2)

Therefore the equation for driving signal is chosen as.

Driving signal:

(3.3)

where P = 5, Q = 7, R = 4, I = 2 satisfy Q = P + R − I.

According to (2.4)–(2.6), the relation of the delays and parameters is expressed as

m₁ − k₁ = n₁, m₂ − k₂ = n₂, k₃ = m₃, k₄ = m₄, k₅ = m₅, k₆ = −n₃, k₇ = −n₄,
β₁ = α₁ + τ_d = γ₁ + τ_d, β₂ = α₂ + τ_d = γ₂ + τ_d, β₃ = α₃ + τ_d, β₄ = α₄ + τ_d, β₅ = α₅ + τ_d, β₆ = γ₃ + τ_d, β₇ = γ₄ + τ_d.

The value of parameters for simulation is adopted as

α = 2.0, W = 100, m₁ = −15.4, m₂ = −16.0, m₃ = −0.35, m₄ = −20.0, m₅ = −18.5,
n₁ = −0.2, n₂ = −0.1, n₃ = −0.25, n₄ = −0.4,
k₁ = −15.2, k₂ = −15.9, k₃ = −0.35, k₄ = −20.0, k₅ = −18.5, k₆ = 0.25, k₇ = 0.4,
τ_d = 3.0, α₁ = 3.4, α₂ = 4.5, α₃ = 6.5, α₄ = 5.3, α₅ = 2.9,
γ₁ = 3.4, γ₂ = 4.5, γ₃ = 2.0, γ₄ = 7.3,
β₁ = 6.4, β₂ = 7.5, β₃ = 9.5, β₄ = 8.3, β₅ = 5.9, β₆ = 5.0, β₇ = 10.3.

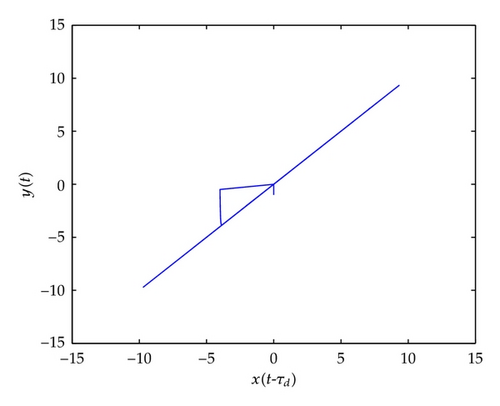
In Figure 1, the portrait of x(t − τ_d) versus y(t) illustrates that the lag synchronization of coupled partly nonidentical systems is established. However their trajectories do not remain in step with each other during a short part of evolution, because they are not in synchronization as t < τ_d.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Portrait of x(t − 3.0) versus y(t).

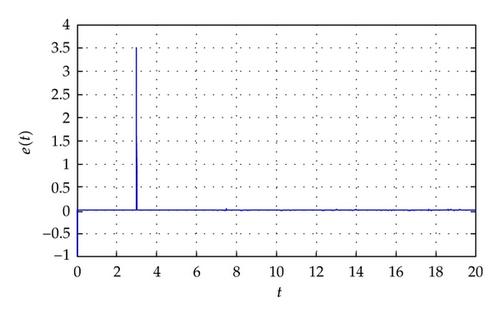
It is clear to observe from Figure 2 that synchronization error e(t) leaps at a sudden as τ_d = 3.0 and vanishes eventually in a short time. Then e(t) stays at zero.

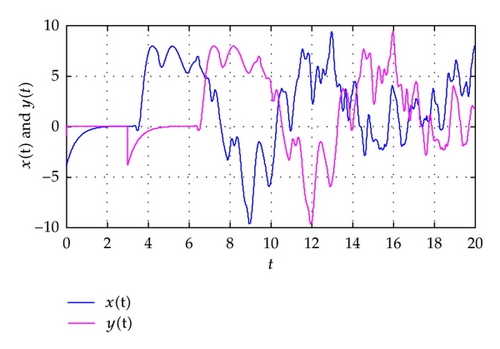
As shown in Figure 3, the slave′s state variable is retarded with the time length of τ_d = 3.0 in comparison with master′s. The desired lag synchronization is realized.

4. Conclusions

In this paper, we have presented a lag synchronization model as well as researched on it. Based on Lyapunov theory, the sufficient conditions of the synchronization model are given. Simulation results of the lag synchronization model are provided to illustrate the effectiveness and feasibility of the proposed method.

Acknowledgments

This work is supported by the National Natural Science Foundation of China (Grants nos. 61170269, 61121061), the Specialized Research Fund for the Doctoral Program of Higher Education (Grant no. 20100005110002) and the Fundamental Research Funds for the Central Universities (Grant no. BUPT2011RC0211).

References

1 Fujisaka H. and Yamada T., Stability theory of synchronized motion in coupled-oscillator systems, Progress of Theoretical Physics. (1983) 69, no. 1, 32–47, https://doi.org/10.1143/PTP.69.32, 699754, ZBL1171.70306.
10.1143/PTP.69.32
CAS Web of Science® Google Scholar
2 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, https://doi.org/10.1103/PhysRevLett.64.821, 1038263, ZBL0938.37019.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
3 Pyragas K., Continuous control of chaos by self-controlling feedback, Physics Letters A. (1992) 170, no. 6, 421–428, 2-s2.0-34250315551.
10.1016/0375-9601(92)90745-8
Web of Science® Google Scholar
4 Cuomo K. M. and Oppenheim A. V., Circuit implementation of synchronized chaos with applications to communications, Physical Review Letters. (1993) 71, no. 1, 65–68, 2-s2.0-12044251580, https://doi.org/10.1103/PhysRevLett.71.65.
10.1103/PhysRevLett.71.65
CAS PubMed Web of Science® Google Scholar
5 Wu C. W. and Chua L. O., A unified framework for synchronization and control of dynamical systems, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (1994) 4, no. 4, 979–998, https://doi.org/10.1142/S0218127494000691, 1314086, ZBL0875.93445.
10.1142/S0218127494000691
Web of Science® Google Scholar
6 Brown R., Rulkov N. F., and Tracy E. R., Modeling and synchronizing chaotic systems from time-series data, Physical Review E. (1994) 49, no. 5, 3784–3800, 2-s2.0-0001581120, https://doi.org/10.1103/PhysRevE.49.3784.
10.1103/PhysRevE.49.3784
CAS Web of Science® Google Scholar
7 Kocarev L. and Parlitz U., General approach for chaotic synchronization with applications to communication, Physical Review Letters. (1995) 74, no. 25, 5028–5031, 2-s2.0-11944272386, https://doi.org/10.1103/PhysRevLett.74.5028.
10.1103/PhysRevLett.74.5028
CAS PubMed Web of Science® Google Scholar
8 Han S. K., Kurrer C., and Kuramoto Y., Dephasing and bursting in coupled neural oscillators, Physical Review Letters. (1995) 75, no. 17, 3190–3193, 2-s2.0-4244104642, https://doi.org/10.1103/PhysRevLett.75.3190.
10.1103/PhysRevLett.75.3190
CAS PubMed Web of Science® Google Scholar
9 Elson R. C., Selverston A. I., Huerta R., Rulkov N. F., Rabinovich M. I., and Abarbanel H. D. I., Synchronous behavior of two coupled biological neurons, Physical Review Letters. (1998) 81, no. 25, 5692–5695, 2-s2.0-0001410639.
10.1103/PhysRevLett.81.5692
CAS Web of Science® Google Scholar
10 Fabiny L., Colet P., Roy R., and Lenstra D., Coherence and phase dynamics of spatially coupled solid-state lasers, Physical Review A. (1993) 47, no. 5, 4287–4296, 2-s2.0-0000565989, https://doi.org/10.1103/PhysRevA.47.4287.
10.1103/PhysRevA.47.4287
CAS PubMed Web of Science® Google Scholar
11 Yu W., Cao J., Wong K.-W., and Lü J., New communication schemes based on adaptive synchronization, Chaos. (2007) 17, no. 3, https://doi.org/10.1063/1.2767407, 2356970, ZBL1163.37387.
10.1063/1.2767407
Web of Science® Google Scholar
12 Rulkov N. F., Sushchik M. M., Tsimring L. S., and Abarbanel H. D. I., Generalized synchronization of chaos in directionally coupled chaotic systems, Physical Review E. (1995) 51, no. 2, 980–994, 2-s2.0-33744833457, https://doi.org/10.1103/PhysRevE.51.980.
10.1103/PhysRevE.51.980
CAS PubMed Web of Science® Google Scholar
13 Huang D. and Guo R., Identifying parameter by identical synchronization between different systems, Chaos. (2004) 14, no. 1, 152–159, https://doi.org/10.1063/1.1635095, 2039637, ZBL1080.37092.
10.1063/1.1635095
PubMed Web of Science® Google Scholar
14 Rosenblum M. G., Pikovsky A. S., and Kurths J., Phase synchronization of chaotic oscillators, Physical Review Letters. (1996) 76, no. 11, 1804–1807, 2-s2.0-4243262725.
10.1103/PhysRevLett.76.1804
CAS PubMed Web of Science® Google Scholar
15 Rosenblum M. G., Pikovsky A. S., and Kurths J., From phase to lag synchronization in coupled chaotic oscillators, Physical Review Letters. (1997) 78, no. 22, 4193–4196, 2-s2.0-0031548743.
10.1103/PhysRevLett.78.4193
CAS Web of Science® Google Scholar
16 Voss H. U., Anticipating chaotic synchronization, Physical Review E. (2000) 61, no. 5 A, 5115–5119, 2-s2.0-0001399571.
10.1103/PhysRevE.61.5115
CAS Web of Science® Google Scholar
17 Mainieri R. and Rehacek J., Projective synchronization in three-dimensional chaotic systems, Physical Review Letters. (1999) 82, no. 15, 3042–3045, 2-s2.0-0000777715.
10.1103/PhysRevLett.82.3042
CAS Web of Science® Google Scholar
18 Pyragas K., Syncronization of coupled timedelaysystems: analytical estimations, Physical Review E. (1998) 58, 3067–3071.
10.1103/PhysRevE.58.3067
CAS Web of Science® Google Scholar
19 Shahverdiev E. M., Sivaprakasam S., and Shore K. A., Lag synchronization in time-delayed systems, Physics Letters, Section A. (2002) 292, no. 6, 320–324, 2-s2.0-0037074482, https://doi.org/10.1016/S0375-9601(01)00824-6.
10.1016/S0375-9601(01)00824-6
CAS Web of Science® Google Scholar
20 Shahverdiev E. M., Sivaprakasam S., and Shore K. A., Lag times and parameter mismatches in synchronization of unidirectionally coupled chaotic external cavity semiconductor lasers, Physical Review E. (2002) 66, no. 3, 037202/1–037202/4, 2-s2.0-41349113563, https://doi.org/10.1103/PhysRevE.66.037202, 037202.
10.1103/PhysRevE.66.037202
CAS Web of Science® Google Scholar
21 Shahverdiev E. M., Nuriev R. A., Hashimov R. H., and Shore K. A., Chaos synchronization between the Mackey-Glass systems with multiple time delays, Chaos, Solitons and Fractals. (2006) 29, no. 4, 854–861, https://doi.org/10.1016/j.chaos.2005.08.128, 2222136, ZBL1142.37330.
10.1016/j.chaos.2005.08.128
Web of Science® Google Scholar
22 Wu C. W. and Chua L. O., A simple way to synchronize chaotic systems with applications to secure communication systems, International Journal of Bifurcation and Chaos. (1993) 3, no. 6, 1619–1627.
10.1142/S0218127493001288
Web of Science® Google Scholar
23 Hoang T. M. and Nakagawa M., Enhancing security for chaos-based communication system with change in synchronization manifolds′ delay and in encoder′s parameters, Journal of the Physical Society of Japan. (2006) 75, no. 6, 2-s2.0-33847295797, https://doi.org/10.1143/JPSJ.75.064801, 064801.
10.1143/JPSJ.75.064801
Web of Science® Google Scholar
24 Hoang T. M., Minh D. T., and Nakagawa M., Chaos synchronization of multi-delay feedback systems with multi-delay driving signal, Journal of the Physical Society of Japan. (2005) 74, no. 8, 2374–2378, 2-s2.0-24644443704, https://doi.org/10.1143/JPSJ.74.2374.
10.1143/JPSJ.74.2374
CAS Web of Science® Google Scholar
25 Hoang T. M. and Nakagawa M., Synchronization of coupled nonidentical multidelay feedback systems, Physics Letters, Section A. (2007) 363, no. 3, 218–224, 2-s2.0-33846705717, https://doi.org/10.1016/j.physleta.2006.11.004.
10.1016/j.physleta.2006.11.004
CAS Web of Science® Google Scholar
26 Khalil H. K., Nonlinear Systems, 2002, 3rd edition, Prentice Hall.
Web of Science® Google Scholar

Citing Literature

All articles

Lag Synchronization of Coupled Multidelay Systems

Abstract

1. Introduction

2. The Schemes of Lag Synchronization

2.1. The Proposed Lag Synchronization Model

2.2. Proof for the Lag Synchronization Model

3. Numerical Simulations

4. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Lag Synchronization of Coupled Multidelay Systems

Abstract

1. Introduction

2. The Schemes of Lag Synchronization

2.1. The Proposed Lag Synchronization Model

2.2. Proof for the Lag Synchronization Model

3. Numerical Simulations

4. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information