Journal of Metallurgy
Volume 2011, Issue 1 895146
Review Article
Open Access

Survey of BGFA Criteria for the Cu-Based Bulk Amorphous Alloys

D. Janovszky, 

Corresponding Author

D. Janovszky

Hungarian Academy of Science-University of Miskolc, Materials Science Research Group, Miskolc-Egyetemvaros H3515, Hungary uni-miskolc.hu

Search for more papers by this author
K. Tomolya, 

K. Tomolya

Hungarian Academy of Science-University of Miskolc, Materials Science Research Group, Miskolc-Egyetemvaros H3515, Hungary uni-miskolc.hu

Search for more papers by this author
M. Sveda, 

M. Sveda

Hungarian Academy of Science-University of Miskolc, Materials Science Research Group, Miskolc-Egyetemvaros H3515, Hungary uni-miskolc.hu

Search for more papers by this author
A. Roosz, 

A. Roosz

Hungarian Academy of Science-University of Miskolc, Materials Science Research Group, Miskolc-Egyetemvaros H3515, Hungary uni-miskolc.hu

Search for more papers by this author
First published: 26 December 2010
https://doi.org/10.1155/2011/895146
Citations: 1
Academic Editor: Livio Battezzati

Abstract

To verify the effect of composition on the bulk glass forming ability (BGFA) of Cu-based alloys, properties have been collected from the literature (~100 papers, more than 200 alloys). Surveying the BGFA criteria published so far, it has been found that the atomic mismatch condition of Egami-Waseda is fulfilled for all the Cu-based BGFAs, the λ value being above 0,3. The Zhang Bangwei criterion could be applied for the binary Cu-based alloys. The Miracle and Senkov criteria do not necessarily apply for Cu based bulk amorphous alloys. The critical thickness versus γ = Tx/(Tg + Tl) plot of Lu and Liu extrapolates to γ = 0.36, somewhat higher than the 0.33 value found in other BGFA alloys. The Park and Kim parameter correlates rather poorly with the critical thickness for Cu based alloys. The Cheney and Vecchino parameter is a good indicator to find the best glass former if it is possible to calculate the exact liquids projection. In 2009 Xiu-lin and Pan defined a new parameter which correlates a bit better with the critical thickness. Based on this survey it is still very difficult to find one parameter in order to characterize the real GFA without an unrealized mechanism of crystallization.

1. Introduction

In the field of metallic materials development the most important aims are to improve the strength, hardness, and the wear resistance without the important decreasing of the plasticity. The copper-based bulk metallic glasses (BMGs) occupy a special place in the family of BMGs owing to their relatively low priced. The serial industrial applications were blocked in the recent past by the small thickness of formed metallic glasses; the maximum size of Cu-based metallic glasses is still restricted to a few mm (12 mm has been reported [1]), at the time being. In order to develop new bulk metallic glasses with larger size there is imperative need for the quantification of GFA.

The BGFA criteria would tell both the type and atomic percentage of the glass forming elements. Inoue defined three empirical rules for the bulk amorphous alloys systems [2]. More and more researchers define further GFA criteria since the first metallic glass was published. There is not a standard definition of GFA up to now; some researcher characterizes the GFA with the critical cooling rate; however the exact measuring of critical cooling rate is very difficult. From the engineering aspect, the critical thickness would be a good choice of the measuring the GFA, nevertheless the critical thickness strongly depends on processing parameters and the impurities. We have selected seven BGFA criteria from the literature, and we have applied them for Cu-based BMGs published so far in the literature (more than 200 alloys). In this work the seven GFA parameters are presented in chronological order.

2. BGFA Criteria

2.1. Egami-Waseda Criterion Structural Factor

In 1984 Egami and Waseda published a correlation between the atomic size ratio of the constituent elements and the glass forming ability for binary systems [3]. This is valid for glass forming under rapid quenching. The λ0 parameter of Egami and Waseda, determined by the product of the minimal glass forming concentration, , and atomic volume mismatch, ΔνB/νA, (see (1)) should be larger than 0.1 for glass forming B element in the A-based amorphous alloy:
()
where rB and rA are the atomic radii. We have calculated this value of λ0 for all Cu-based bulk amorphous alloys with ci concentration of the ith element in the alloys and the volume mismatch νi/νA. The values of λ0 were found to be above 0.2 for all the BMG alloys reported. The overage values of λ0 for different bulk amorphous systems are in Table 1.
Table 1. The overage value of λ0 for some representative Cu-based bulk amorphous alloy system.
Alloy λ0 Alloy λ0
Cu-Zr-Ti 0,352 Cu-Zr-Al 0,485
Cu-Zr-Ti-Ni 0,278 Cu-Hf 0,509
Cu-Zr-Ti-Hf 0,451 Cu-Hf-Ti 0,400

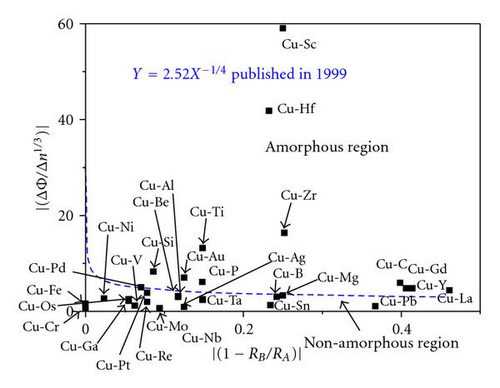
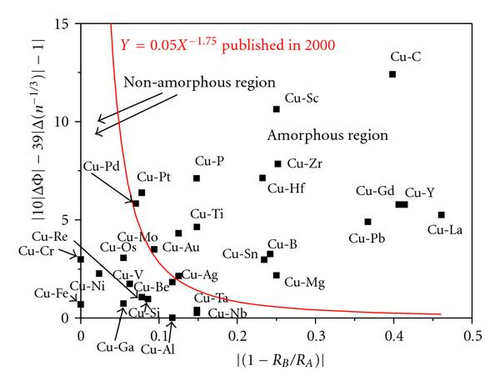
2.2. Bangwei Criterion Based on Miedema’s Model

In 1999 Bangwei et al. [4] have invented a combination of the size factor (X) and an electron factor (Y) which are formulated with the help of the atomic mismatch and chemical coordinates of Miedema [5], The X and Y are given as follows:
()
()
where ΔΦ = ΦA − ΦB, , rx, rA are the atomic radii, and Φ and n are Miedema’s coordinates [6], respectively. The element A is always the copper. Later they changed the electron factor [7] to
()
For glass forming ability both the size and electron factor should be large. When only one parameter is large, then the production of fully amorphous alloy needs very high cooling rate. We have calculated these factors for 31 binary alloys and plotted them in Figures 1(a) and 1(b), using the electron factors given by (3) and (4), respectively. The equations for dividing the amorphous and nonamorphous regions are given in the figures. Although these plots predict that the Cu-metalloid binary alloys are good glass formers, they usually have not been prepared by melts spinning as to the authors knowledge. The reason of this is complex (it can be accounted for physical properties in the liquid state e.g., immiscibility of the elements). Nevertheless, these plots are useful in predicting the good GFA for Cu and early transition elements combinations.
Details are in the caption following the image
Figure 1 (a)
Open in figure viewerPowerPoint
Bangwei plot for Cu-based binary alloys using equations published in 1999 (a) and 2000 (b).
Details are in the caption following the image
Figure 1 (b)
Open in figure viewerPowerPoint
Bangwei plot for Cu-based binary alloys using equations published in 1999 (a) and 2000 (b).

2.3. Senkov-Miracle Criterion Structural Factor

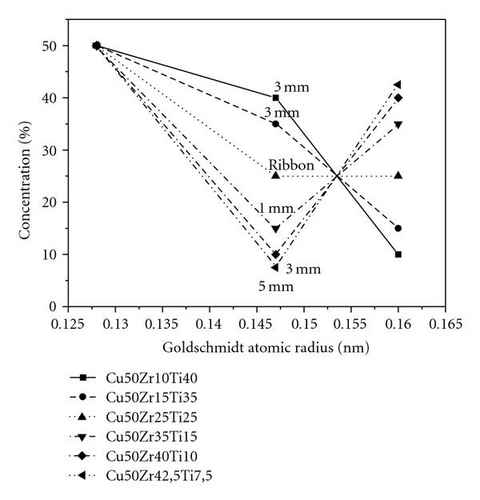
In 2001 Senkov and Miracle examined different bulk amorphous alloys based on Mg, Cu, Zr, Al, Ni, Fe, and Pd. They represented the concentration of elements versus the atomic size, obtaining different distributions for bulk amorphous alloys. They concluded that a concave upward plot generally characterizes the good glass forming ability [11]. Unfortunately, critical cooling rates and critical thicknesses are given only in limited number of publications [6, 8]. In Figure 2 numbers note the maximum thickness of the amorphous alloys. It can be seen that the very similar plots have different maximum thickness (Figure 2(a)). For the same maximal thickness (e.g., 3 mm) the curve plotted in Figure 2(b) could show concave upward shape or concave downward shape tendency. Based on these findings we can assert that the Senkov and Miracle criterion does not apply to Cu-based bulk amorphous alloys.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Atomic distributions in several Cu-based amorphous alloys: (a) alloys [8], (b) alloys [6].
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Atomic distributions in several Cu-based amorphous alloys: (a) alloys [8], (b) alloys [6].

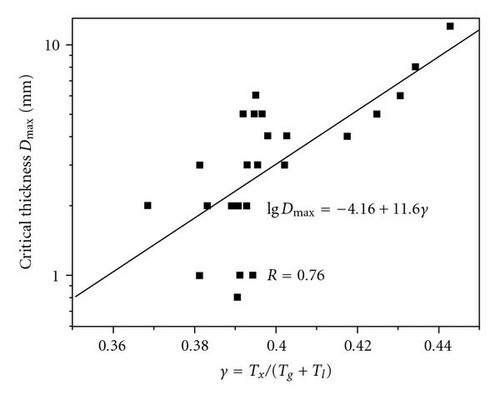
2.4. Lu and Liu Criterion Based on the Measured Thermal Parameters

The critical cooling rate for glass formation (Rc) may be a proper measure of the GFA of the alloy. The Rc is the minimum cooling rate necessary to keep the melt without precipitation of any crystals during solidification. In 2002 Lu and Liu defined a new GFA parameter (γ), which depends on the glass temperature (Tg), crystallization temperature (Tx), and the liquidus temperature (Tl) [12]. This GFA parameter is not considering the properties of the elements but it characterizes the properties of already produced amorphous alloys;
()
In the literature there is only a small amount of datas relative to the critical cooling rate, so alternatively the maximum section size of BMG (Dmax ) has often been used as a measure of GFA. We have selected 25 different Cu-based bulk amorphous alloys, where the maximum diameter has been examined and the same heating rate (40 K/min) has been used in the measurements of thermal parameters [6, 9, 10]. The relationship between the γ  value and Dmax  is shown in Figure 3. The critical thickness for bulk amorphous alloy can be estimated by using the formula
()
The value of the statistical correlation parameter has evidenced a poor correlation in our calculations.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Critical thickness (Dmax ) as a function of the γ  parameter [6, 9, 10].

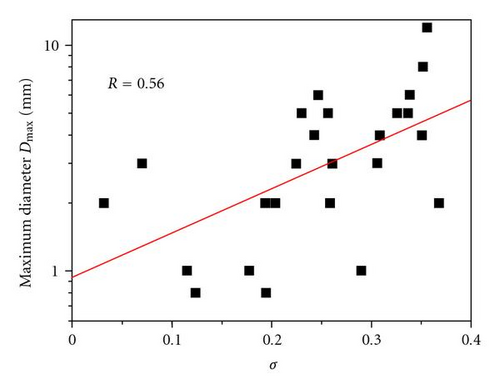
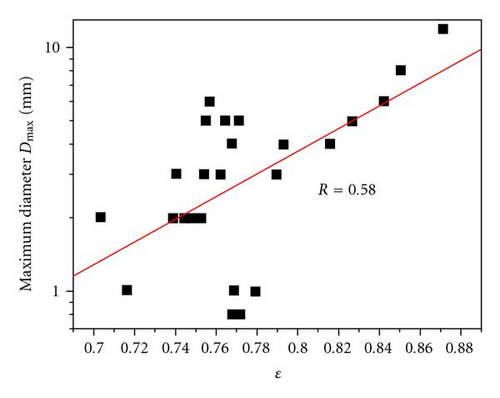
2.5. Park and Kim Criterion Structural Factor

In 2005 Park et al. proposed to bring in a parameter (σ) for GFA of ternary alloys [13]. They combined the effects of melting temperature depression and atomic size mismatch between the constituting elements;
()
where , xi and stand for the mole fraction and melting point, respectively, of the ith component in an n-component alloy system. A P′  parameter represents the effective atomic mismatch of each solute atom;
()
The σ parameter exhibits a very poor correlation with the critical thickness in the case of Cu-based alloys (Figure 4(a)). Later Park and Kim mention a new ε parameter [9];
()
The new ε  parameter also shows a poor correlation for GFA, although the ε parameter was an attempt to calculate the stability of the liquid (Figure 4(b)).
Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
A Correlation between σ (a,) and ε  (b) for GFA and Dmax  for Cu-based BMG-forming alloys [6, 9, 10].
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
A Correlation between σ (a,) and ε  (b) for GFA and Dmax  for Cu-based BMG-forming alloys [6, 9, 10].

2.6. Cheney and Vecchino Parameter Based on Phase Diagram

The individual composition of the bulk glassy alloys with high GFA usually is almost identical to a deep eutectic composition. However the liquidus projection of amorphisable alloys is not well known, especially in case of the multicomponent systems. In 2007 Cheney and Vecchino used ThermoCalc TCC software in order to calculate the liquidus temperature. They proposed an α parameter in order to describe the depth of an eutectic composition within an alloy system:
()
where xi and Ti stand for the mole fraction and melting temperature of element i and Tl actual liquids temperature. α value of an eutectic is greater than one, and the peak in the α parameter profile is the ideal composition for bulk glass design. Based on this calculation the best glass formers are shown to have large regions where the alpha parameter is higher than 1.

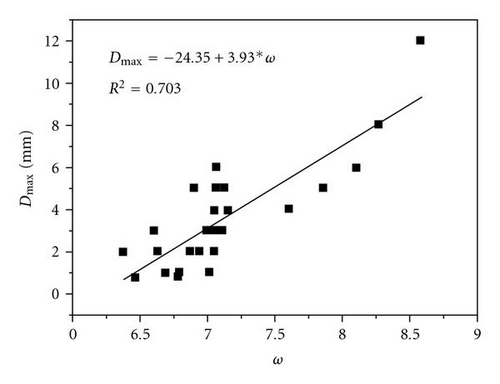
2.7. Xiu-lin and Pan Criterion Based on Thermodynamic Approach

In 2009 Xiu-lin and Pan proceeded from Thomson and Spaepen’s expression and they have defined a ω parameter:
()
where Tx is the crystallization temperature and Tl liquids temperature. It is a linear function between ω and the critical section thickness (Zc), according to authors. The new ω  parameter shows a better correlation for GFA although this parameter was formed with much approximation and neglect (Figure 5). In one alloy system this criterion is a good aidance in order to find the composition with best GFA, but this parameter is not adaptable to compare two different alloy systems.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
A Correlation between ω and Dmax  for Cu based BMG-forming alloys [6, 9, 10].

3. Conclusions

Following the studies of articles we have concluded that composing a good criterion for BGFA is very difficult. First of all it is not a standard definition for GFA parameter; generally it is measured by critical thickness which is depended from technologies. Most criteria are based on atomic structure and thermodynamics but this is a kinetic problem. The following complements need to be mentioned:
  • (1)

    The critical cooling rate is less studied in the literature although it is an important aspect during the solidification. The authors of the present work believe that the method applies for crystalline alloys, estimating the cooling rate from the secondary dendrite arm distances [14–16].

  • (2)

    The critical thickness was given only in some cases, often without mentioning the measuring error.

  • (3)

    The characteristic temperatures (Tg, Tx, and  Tl) measured by DSC and DTA depend on the heating rates. One may use only those temperatures which were measured with the same heating rate. Especially, the liquidus temperature is affected by a great error.

  • (4)

    The composition of ingots has not been analysed in general; there are different data relative to the same nominal composition. For example Tg changes from 700 K [17] to 724 K [9] at 40 K/min heating rate and the liquid temperature changes from 1152 K [17] to 1175 K [9] at 10 K/min heating rate in the case of Cu60Zr30Ti10 alloy.

  • (5)

    The BGFA parameters do not take the undercooling of the crystallize phases into consideration. Every phase has a different undercooling and a critical cooling rate.

As a summary of this survey we can state that in order to characterize the real GFA we have to establish a real GFA criterion based on the mechanism of crystallisation which is not one single indicator but some associated indicators.

To our knowledge with numerical simulation methods it has not been possible to give a reliable forecast for the mechanism of nucleus formation with the ab inito method.

Researchers have to do numerous experiments to finding out the best BMG composition.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.