Journal of Applied Mathematics
Volume 2011, Issue 1 721349
Research Article
Open Access

Dispersion of Love Waves in a Composite Layer Resting on Monoclinic Half-Space

Sukumar Saha, 

Corresponding Author

Sukumar Saha

BAS Division, CSIR-Central Road Research Institute, New Delhi 110025, India csir.res.in

Search for more papers by this author
First published: 17 July 2011
https://doi.org/10.1155/2011/721349
Citations: 1
Academic Editor: M. A. Fontelos

Abstract

Dispersion of Love waves is studied in a fibre-reinforced layer resting on monoclinic half-space. The wave velocity equation has been obtained for a fiber-reinforced layer resting on monoclinic half space. Shear wave velocity ratio curve for Love waves has been shown graphically for fibre reinforced material layer resting on various monoclinic half-spaces. In a similar way, shear wave velocity ratio curve for Love waves has been plotted for an isotropic layer resting on various monoclinic half-spaces. From these curves, it has been observed that the curves are of similar type for a fibre reinforced layer resting on monoclinic half-spaces, and the shear wave velocity ratio ranges from 1.14 to 7.19, whereas for the case isotropic layer, this range varies from 1.0 to 2.19.

1. Introduction

Fiber-reinforced composite materials have become very attractive in many engineering applications recently due to their superiority over the structural materials in applications requiring high strength and stiffness in light-weight material. Consequently, the characterization of their mechanical behavior is an utmost requirement. The monoclinic system is the largest symmetry system with almost a third of all minerals belonging to one of its classes. This system contains two nonequal axes (a and b) that are perpendicular to each other and a third (c), that is, inclined with respect to the axes. The a and c axis lie in a plane. The a-c plane can be, but is not always, a mirror plane with left side of b-axis a reflection of the right side. Fledspar which is an example of monoclinic material is the name of a group of rock-forming minerals which make up as much as 60% of earth’s crust. Feldspars crystallize from magma in both intrusive and extrusive igneous rocks, and they also can occur as compact minerals, as veins, and are also present in many types of metamorphic rock. Rock formed entirely of plagioclase feldspar is known as an orthosite. Feldspars are also found in many types of sedimentary rock. The wave propagation in reinforced medium was studied by Chattopadhyay and Choudhury [1] and in crystalline monoclinic plate was studied by Chattopadhyay and Bandyopadhyay [2]. Propagation of elastic waves in laminated composite plates was studied by Datta et al. [3]. Chattopadhyay et al. [4] studied the propagation, reflection, and transmission of shear waves in monoclinic media and obtained a dispersion equation for a monoclinic layer overlying monoclinic half-space. Besides these, a large number of papers on elastic wave propagation have been published in different journals. Without going into details of research works in this field, we mention papers by Kim [5] and Nayfeh [6]. In this paper, we have computed the ranges of shear wave velocity ratio and the corresponding wave numbers for Love waves at a layer of fiber-reinforced material resting on monoclinic half-space and compared them with shear wave velocity ratio of Love waves at isotropic layer resting on monoclinic half-space. Using these values the dispersion curves have also been obtained.

2. Formulation of the Problem

The constitutive equations for fibre-reinforced linearly elastic medium whose referred direction is that of a are (Spencer [7])
(2.1)
where τij, are components of stress, eij, are components of infinitesimal strain, and aij are components of a, all referred to Cartesian coordinates. The vector a may be a function of position. The coefficients λ, μL, μT, α, and β are elastic constants with dimension of stress. If a is so chosen that its components are (0,0, 1). The stress components (2.1) become
(2.2)
where 2eij = (ui,j + uj,i) and ui  (i = 1,2, 3) are the displacement components.
In this problem, we consider a fiber-reinforced of anisotropic layer −h ≤ x2 ≤ 0 resting on the monoclinic half-space (x2 ≥ 0) in the x3 − x2 plane. The x3-axis is chosen parallel to the layer in the direction of propagation of the disturbance. The strain-displacement relations for a monoclinic crystal medium are
(2.3)
where , and are displacement components in the directions x1,   x2, and x3, respectively, and Si  (i = 1,   2, …6) are the strain components. The stress-strain relations for a rotating x2-cut plate of quartz which exhibits monoclinic symmetry with x1 being the diagonal axis are
(2.4)
where Ti  (i = 1,2, 3) are the normal stresses Ti  (i = 4,5, 6) are the shearing stresses, Cij = Cji (i, j = 1,2, 3,4, 5,6) are the elastic constants. In the study of seismic waves, when s-pulses are polarized so that all particles of the substance move horizontally during its passage, the wave motion is called SH-wave. Our problem is to investigate the propagation of such waves in the media which consist of two separate media in which upper medium is a layer of thickness h, and the lower one is monoclinic half-space.

3. Solution of the Problem

For wave propagating in the x3-direction and causing displacements in the x1-direction only, we assume that u2 = u3 = 0 and u1 = u1(x3, x2, t) = u1(x2, x3, t). For the shear wave propagating in the x3-x2 plane, ∂/∂x1 = 0. So the equation of motion for shear wave takes the form
(3.1)
Putting the values of τ12 and τ13, the above equation takes the form given below
(3.2)
For wave changing harmonically u1(x3, x2, t) = u(x2)exp [i(kx3 − ωt)], where k = wave number, ω = (kc) is the angular frequency, and c is the speed of simple harmonic waves of wavelength (2π/k). Substituting this value of u1 in the equation of motion, it transforms into
(3.3)
The solution of this equation is
(3.4)
Therefore,
(3.5)
Equation of motion for the lower half-space has been obtained by
(3.6)
using the values of T5 and T6. Finally, the equation has been obtained as
(3.7)
where is the displacement in the x1 direction in the lower half-space. We assume that
(3.8)
is the solution of the above differential equation. So, by substituting this to the above equation, we obtain the solution as
(3.9)

3.1. Boundary Conditions

The boundary conditions in the plane x2 = −h at the top of the system
(3.10)
At the interface, that is, at x2 = 0,
(3.11)
(3.12)
From (3.10),
(3.13)
From (3.11), we obtain
(3.14)
From (3.12), we obtain
(3.15)
Therefore,
(3.16)
So,
(3.17)
where
(3.18)
Finally,
(3.19)
this equation (3.19) gives the velocity of love wave in an elastic fiber-reinforced layer of finite thickness h resting on the monoclinic half-space which may be naturally a stable rock layer of large thickness. So, it is a possible case that a road of fiber-reinforced composite material has been constructed on a rock surface. To make it seismically stable, the knowledge of probable velocity of Love wave will be a necessary precondition. In this context, this study will be helpful. The real root of this equation can be found for the values of c given below
(3.20)
If we transform the upper and lower layer as isotropic medium with different rigidity and density, the wave equation (3.19) takes the form shown below, by taking C56 = 0,   C66 = C55 = μ0,    and μT = μL = μ,
(3.21)
where rigidity and density for upper and lower media are μ, ρ and μ0, ρ′, respectively. This equation is well-known Love wave equation for classical case. By taking, C66 = μT  ,     C55   =   μL,   C56   = 0, the wave equation (3.19) transforms to the case of wave equation for a fiber-reinforced layer resting on fiber-reinforced half-space derived by Sengupta and Nath [8].

4. Numerical Results and Discussion

The range of shear wave velocity ratio of Love wave has been obtained from (3.20), and within this range, the corresponding values of kh are obtained from (3.19) by considering different material constants of fiber-reinforced layer and monoclinic half-space. These values have been plotted to obtain the shear wave velocity ratio curve. We have obtained a set of shear wave velocity ratio curve for fiber-reinforced layer resting on half-spaces of different materials (monoclinic and isotropic). Similarly, a set of shear wave velocity curves for isotropic layer resting on monoclinic and isotropic half-spaces have also been obtained. These are specified in details in Cases 2 and 1, respectively, below.

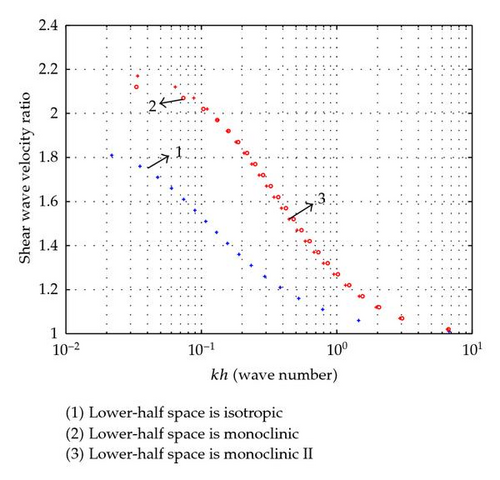
Case 1. Here we have considered three sets of arrangements; in all these, top layer is isotropic-I, and lower half-spaces are (i) isotropic-II with different material constants from isotropic-I, (ii) lower half-space is monoclinic, and (iii) lower half-space is monoclinic II, respectively. The material constants are = 6 × 109 N/m2, ρ = 2300 kg/m3 for isotropic-I and   μ = 25 × 109 N/m2, ρ = 2700 kg/m3 for isotropic-II. The material constants for monoclinic are as C55   = 0.94 × 1011 N/m2, C56   = −0.11 × 1011 N/m2, C66 = 0.93 × 1011 N/m2, and ρ = 7800 kg/m3 and for monoclinic-II are C55   = 0.60 × 1011 N/m2, C56   = 0.09 × 1011 N/m2, C66   = 0.75 × 1011 N/m2, ρ = 4700 kg/m3given by Tiersten [9]. Using these values, shear wave velocity ratio curves have been plotted for corresponding values of kh obtained from (3.19). The range of values for shear wave velocity ratio and kh are given in Table 1, and curves are given in Figure 1.

Table 1. Ranges of shear wave velocity ratio and ranges of kh for isotropic layer.
Isotropic layer resting on half-space Range of shear wave velocity ratio Range of kh
Isotropic 1.0–1.85 Large value–0.00058
Monoclinic 1.0–2.1922 Large value–0.013
Monoclinic II 1.0–2.1949 Large value–0.06071
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Shear wave velocity ratio curve for Love waves at isotropic layer resting on monoclinic half-Space.

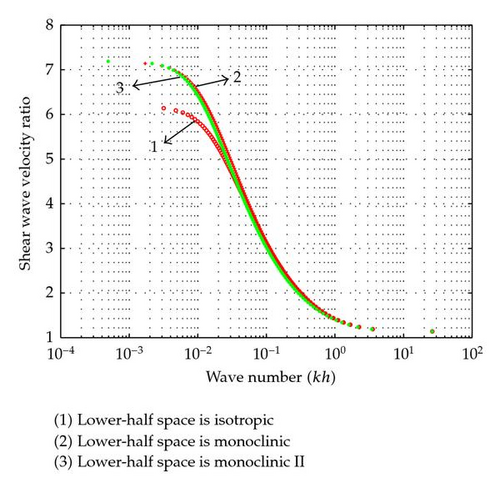
Case 2. In this case, we have plotted three dispersion curves as in Case 1. Here the upper layer is taken as fibre-reinforced layer, and the lower half-spaces are taken as in Case 1 of three separate arrangements, and the material constants are the same as earlier. The material constants for fibre-reinforced layer are  μL = 2.45 × 109 N/m2, μT = 1.89 × 109 N/m2, and  ρ = 7800 kg/m3. Shear wave velocity ratio curve for Love waves at fibre-reinforced layer has been plotted for all these three cases and shown in Figure 2, and the ranges of shear wave velocity ratio and wave number are shown in Table 2.

From the results it has been observed that shear wave velocity ratio for Love waves at fibre-reinforced layer is very much higher than at isotropic layer.

Table 2. Ranges of shear wave velocity ratio and kh for fiber-reinforced layer.
Reinforced layer resting on half-space Range of shear wave velocity ratio Range of kh
Isotropic 1.14–6.15 Large value–0.0028
Monoclinic 1.14–7.16 Large value–0.0125
Monoclinic II 1.14–7.19 Large value–0.0110
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Shear wave velocity ratio curve for Love waves at fibre-reinforced layer resting on monoclinic half-Space.

5. Conclusions

From the curves plotted and results tabulated, it has been clearly observed that the shear wave velocity ratio for a fiber-reinforced layer resting on any layer whether it is isotropic or monoclinic is always much higher than on the isotropic layer resting on similar half-spaces. For the case of fiber-reinforced layer, shear wave velocity ratio ranges from 1.14 to 6.15, 1.14 to 7.16, and 1.14 to 7.19, for isotropic half-spaces, monoclinic and monoclinic-II half-spaces, respectively. In the contrary for the case of an isotropic layer, the shear wave velocity ratio ranges from 1.0 to 1.85, 1.0 to 2.19, and 1.0 to 2.19 for the case isotropic, monoclinic, and monoclinic-II half-spaces, respectively.

Acknowledgments

S. Saha is very much thankful to Director CRRI, for his permission to publish this paper. S. Saha is also very much thankful to the reviewer for valuable comments to modify this paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.