International Journal of Differential Equations
Volume 2011, Issue 1 619623
Research Article
Open Access

On Spectrum of the Laplacian in a Circle Perforated along the Boundary: Application to a Friedrichs-Type Inequality

G. A. Chechkin, 

G. A. Chechkin

Department of Differential Equations, Faculty of Mechanics and Mathematics, Moscow Lomonosov State University, Moscow 119991, Russia msu.ru

Narvik University College, Postboks 385, 8505 Narvik, Norway hin.no

Search for more papers by this author
Yu. O. Koroleva, 

Corresponding Author

Yu. O. Koroleva

Department of Differential Equations, Faculty of Mechanics and Mathematics, Moscow Lomonosov State University, Moscow 119991, Russia msu.ru

Department of Engineering Science and Mathematics, Luleå University of Technology, 971 87 Luleå, Sweden ltu.se

Search for more papers by this author
L.-E. Persson, 

L.-E. Persson

Narvik University College, Postboks 385, 8505 Narvik, Norway hin.no

Department of Engineering Science and Mathematics, Luleå University of Technology, 971 87 Luleå, Sweden ltu.se

Search for more papers by this author
P. Wall, 

P. Wall

Department of Engineering Science and Mathematics, Luleå University of Technology, 971 87 Luleå, Sweden ltu.se

Search for more papers by this author
First published: 15 November 2011
https://doi.org/10.1155/2011/619623
Citations: 1
Academic Editor: Mayer Humi

Abstract

In this paper, we construct and verify the asymptotic expansion for the spectrum of a boundary-value problem in a unit circle periodically perforated along the boundary. It is assumed that the size of perforation and the distance to the boundary of the circle are of the same smallness. As an application of the obtained results, the asymptotic behavior of the best constant in a Friedrichs-type inequality is investigated.

1. Introduction

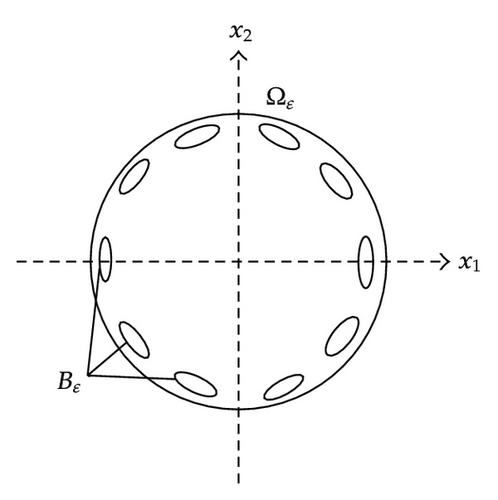
We study a two-dimensional eigenvalue problem for the Laplace operator in a unit circle periodically perforated along the boundary. It is assumed that the size of perforation and the distance to the boundary of the circle are of the same smallness. The asymptotic behavior of the spectrum of the considered boundary-value problem is investigated in this paper. We construct and verify the asymptotic expansion for the eigenvalues with respect to the small parameter describing the microinhomogeneous structure of the domain. A similar problem was considered in [1] for the case of perforation located along the plane part of the boundary. The case studied in this paper is much more complicated since the eigenvalues of multiplicity more than one can appear. The technique for asymptotic analysis of such kind of problem can be found, for example, in [2, 3].

The obtained results are used for asymptotic expansion of the best constant in a Friedrichs-type inequality for functions from the space H1, vanishing on the boundary of the perforation and satisfying homogeneous Neuman condition on the boundary of the circle. Analogous questions concerning the asymptotic behavior of the best constant in Friedrichs-type inequality in domains having microinhomogeneous structure in a neighborhood of the boundary were studied in [1, 4–11]. In the remaining part of this introduction, we will give a short description of some of the most important results in these papers to put the results obtained in this paper into a more general frame.

In paper [4], the authors proved a Friedrichs-type inequality for functions, having zero trace on the small periodically alternating pieces of the boundary of a two-dimensional domain. The total measure of the set, where the function vanishes, tends to zero. It turns out that for this case the constant in the Friedrichs-type inequality is bounded. Moreover, the precise asymptotics of the constant in the derived Friedrichs-type inequality is described as the small parameter characterizing the microinhomogeneous structure of the boundary, tends to zero.

Paper [5] is devoted to the asymptotic analysis of functions depending on the small parameter, which characterizes the microinhomogeneous structure of the domain where the functions are defined. The authors considered a boundary-value problem in a two-dimensional domain perforated nonperiodically along the boundary in the case when the diameter of circles and the distance between them have the same order. In particular, it was proved that the Dirichlet problem is the limit for the original problem. Moreover, some numerical simulations were used to illustrate the results. As an application, a Friedrichs-type inequality was derived for functions vanishing on the boundary of the cavities. It was proved that the constant in the obtained inequality is close to the constant in the inequality for functions from . The three-dimensional case of the same problem is considered in [8].

In paper [9], the author considered a three-dimensional domain, which is aperiodically perforated along the boundary in the case when the diameter of the holes and the distance between them have the same order. A Friedrichs-type inequality was derived for functions from the space H1 vanishing on the boundaries of cavities. In particular, it was shown that the constant in the derived inequality tends to the constant of the classical inequality for functions from when the small parameter describing the size of perforation tends to zero.

Paper [1] (see also [7]) deals with the construction of the asymptotic expansion for the first eigenvalue of a boundary-value problem for the Laplacian in a perforated domain. This asymptotics gives an asymptotic expansion for the best constant in a corresponding Friedrichs-type inequality.

Paper [11], is devoted to the Friedrichs-type inequality, where the domain is periodically and rarely perforated along the boundary. It is assumed that the functions satisfy homogeneous Neumann boundary conditions on the outer boundary and that they vanish on the perforation. In particular, it is proved that the best constant in the inequality converges to the best constant in a Friedrichs-type inequality as the size of the perforation goes to zero much faster than the period of perforation. The limit Friedrichs-type inequality is valid for functions in the Sobolev space H1.

Some generalizations of Friedrichs-type inequalities are Hardy-type inequalities. There exist several books devoted to this topic, see [12–16]. The first attempts to generalize the classical results concerning Hardy-type inequalities in fixed domains to domains with microinhomogeneous structure one can find in [6, 10].

Paper [6] deals with a three-dimensional weighted Hardy-type inequality in the case when the domain Ω is bounded and has nontrivial microstructure. It is assumed that the small holes are distributed periodically along the boundary. The main result is the validity of a weighted Hardy-type inequality for the class of functions from the Sobolev space H1 having zero trace on the small holes under the assumption that a weight function decreases to zero in a neighborhood of the microinhomogenity on the boundary.

In paper [10], the author derived a new two-dimensional weighted Hardy-type inequality in a rectangle for the class of functions from the Sobolev space H1 vanishing on small alternating pieces of the boundary. The dependence of the best constant in the derived inequality on the small parameter describing the size of microinhomogenity was established.

This paper is organized as follows: in Section 2 we give all necessary definitions and state the spectral problem. Section 3 is devoted to the construction of the leading terms of asymptotic expansion, while the complete expansions for the simple and multiple eigenvalues are constructed in Sections 4 and 5, respectively. The verification of the constructed asymptotics is given in Section 6. Finally, in Section 7, the obtained results are applied to describe the asymptotic behavior for the best constant in a Friederichs-type inequality considered in a perforated domain.

2. Preliminaries

Consider a unit circle Ω centered at the origin. We introduce the polar system of coordinates (θ, r) in Ω. Introduce a small parameter ɛ = 2/N,   N ≫ 1, and consider the open set Bɛ which is the union of small sets periodically distributed along the boundary. Each of these small sets can be obtained from the neighboring one by rotation about the origin through the angle ɛπ. Finally, we define and ∂Bɛ = Γɛ, see Figure 1. Let us describe the geometry of Bɛ in details. Consider the semi-strip:
()
Let B be an arbitrary two-dimensional open domain with a smooth boundary that is symmetric the vertical axis and lies in a disk of a fixed radius a < 1 centered at the point (0,1), see Figure 2. Let Ba be the union of the π-integer translations of B along the axis ξ1. Then we define Bɛ as the image of Ba under the mapping θ = ɛξ1, r = 1 − ɛξ2.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Perforated circle.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Cell of periodicity.
Consider the following spectral problem:
()
The problem,
()
is the limit one for (2.2). This fact can be established analogously as in [17, 18], by using the same technique.

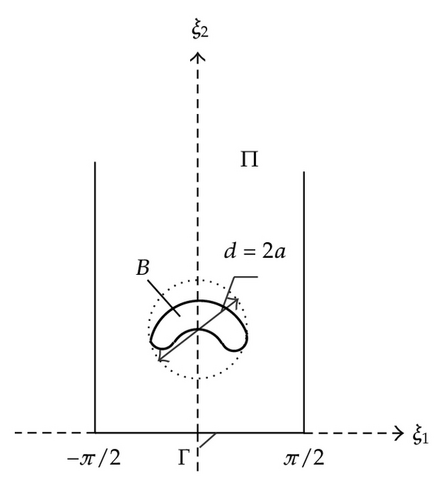
Remark 2.1. In particular, it can be proved that the number of eigenvalues (bearing in mind the multiplicities) of the original problem converging to the eigenvalue of the limit (homogenized) problem is equal to the multiplicity of the mentioned eigenvalue of the limit problem (for the method of proof see, e.g., [19]).

Remark 2.2. The limit spectral problem (2.3) is studied very well. In particular, if the eigenvalue λ0 is simple, then the corresponding eigenfrequency of (2.3) is the zero-point of the Bessel-function 𝒥0, and the corresponding eigenfunction has the form 𝒥0(k0r). One can find the definition of Bessel-functions, for example, in [20, Section 4.7].

The goal of this paper is to construct and verify the asymptotic expansion for the eigenvalues of (2.2). The obtained asymptotics is used for studying the behavior of the best constant in a Friedrichs-type inequality for functions belonging to the Sobolev class H1(Ωɛ, Γɛ) (see the definition of H1(Ωɛ, Γɛ) in Section 7). One of the main results of this paper is the following asymptotics for λɛ converging to λ0:
()
where λi are some fixed constants which can be calculated according to (4.23) and (4.15) in the case of simple λɛ and according to (5.10) and (4.15) when λɛ is of multiplicity two. In particular, λ1 < 0 which implies that λɛ < λ0.

3. Construction of the Leading Terms of the Asymptotic Expansion

Suppose that λ0 is the simple eigenvalue for (2.3) and the corresponding eigenfunction u0 is normalized in L2(Ω). Our aim is to construct the leading terms of the asymptotic expansions for λɛ converging to λ0 as well as uɛ converging to u0. We use the method of boundary-layer functions (see [21]) for this purpose. We are looking for eigenvalues and eigenfunctions in the following form:
()
where ξ = (ξ1, ξ2),  ξ1 = θ/ɛ,  ξ2 = (1 − r)/ɛ, and
()
Substituting the first expansion from (3.1) and the sum u0 + ɛu1 from the second expansion in (2.2) and equating terms at the same power of ɛ, we get the equation for u1:
()
The existence of the solution for (3.3) is given in the following proposition.

Proposition 3.1. For any λ1, there exists the smooth solution of (3.3) satisfying the boundary condition

()

Proof. The existence of the smooth solution follows from the classical results on regular solutions of elliptic equations (see e.g., [22]). In order to get u1 as the unique solution, one can add the condition of mutual orthogonality:

()

By multiplying (3.3) by u0, integrating (3.3) over Ω, and twice integrating by parts the obtained equation, we find that

()
Taking into account the fact that u0 is the normalized (in L2(Ω)) solution of (2.3) and since u1 satisfies (3.5), we can deduce that
()
Then (3.7) leads to (3.4) and the proof is complete.

However, the approximation u0 + ɛu1 does not satisfy the condition on Γɛ. This forces us to introduce an additional term α0v in second expansion of (3.1) to satisfy the appropriate boundary condition. We assume that the function v has exponential decay as ξ2 → ∞ and is π-periodical with respect to ξ1. Under this assumption, α0v “almost” does not destroy (2.2) in the sense that the norm of additional contribution is small. The rigorous explanation is given in Section 6. Proceeding, we have that
()
Taking into account (2.3) and (3.3), we see that v has to satisfy the equation
()
Rewrite Δx in polar coordinates and pass to the ξ-variables in the argument of v:
()
Finally, replacing formulas 1/(ɛ − ɛ2ξ2) and 1/(1 − ɛξ2) 2 with Taylor series with respect to ɛ, substituting the obtained formula for Δx(α0v) in (3.9), and equating terms at ɛ−2, we deduce that
()
Now we derive the boundary conditions for function v. Substituting the second series from (3.1) in boundary conditions from (2.2) and using (3.2), we have
()
which implies that
()
Taking into account (3.4), we derive the boundary conditions for v on ∂B and on Γ:
()
Summing up (3.11) and (3.14), we get the following boundary-value problem for v:
()
Define the function Y as the solution of the following boundary-value problem in the cell of periodicity:
()
It was proved in [7] that there exists the solution of (3.16), which is even with respect to ξ1 and has the asymptotics:
()
where
()
and |B| is the area of the domain B.

The following lemma gives the conditions to obtain v as an exponentially decaying function as ξ2 → ∞.

Lemma 3.2. Assume that F is π-periodic with respect to ξ1 function with exponential decay as ξ2 → ∞, and let v be a π-periodic solution of the boundary-value problem:

()
with finite Dirichlet integral in Π. Then there exists the unique weak solution, which has asymptotics . To obtain v as a function with exponential decay as ξ2 → ∞, it is necessary and sufficient to have
()

Proof. The existence of the solution with asymptotics follows from the classical results on elliptic boundary-value problems in cylindric domains (see, e.g., [23] and [24, Chapters 2, 5]). Let us verify (3.20). Define ΠR = Π∩{0 < ξ2 < R} and ΓR = {ξ : −π/2 < ξ1 < π/2, ξ2 = R}. By multiplying the equation from (3.15) by Y, integrating it over , and using the property of Y, we get that

()
Passing to the limit as R → ∞, we obtain that
()
This can be rewritten as
()
Then v has exponential decay as ξ2 → ∞ if and only if C = 0 which is equivalent to (3.20). The proof is complete.

In order to obtain v as function with exponential decay as ξ2 → ∞, one must have
()
where we denote . However, (3.24) implies that
()
Integrate the identities :
()
Passing to the limit as R → ∞, we find that
()
Then (3.25) and (3.27) together with Remark 2.2 imply that
()

4. Complete Expansion in the Case of the Simple Eigenvalue λ0

Assume that λ0 is the simple eigenvalue of the limit problem. Now we construct the complete expansion in the following form:
()
where χ is a smooth cutoff function, which equals to one when 1/2 < r < 1 and zero when r < 1/4:
()
()
Here ,vi(ξ) are π-periodic in ξ1 functions with exponential decay as ξ2 → ∞. One can easily show that (4.2) solves the equation:
()
if and only if .
We are looking for , which solves the equation:
()
If (4.4) and (4.5) are satisfied, then uɛ from (4.1) is the solution of
()
where . Our aim is to construct so that F will be of small order as ɛ → 0. This is the reason why we need to have vi as exponentially decaying functions.
Now we derive the formula for the Laplacian in ξ-variables:
()
By substituting the Taylor series for the functions
()
in (4.7), we get the final formula for Δx:
()
Substituting (2.4) and (4.3) in (4.5) and taking into account (4.9), we deduce the following formula:
()
By equating terms of the same power of ɛ, we obtain that
()
Consider now the boundary conditions from (2.2). According to the property of χ,
()
in a small neighborhood of ∂Ω. Moreover, on ∂Ω, it yields that
()
We assume that the function k(ɛ) has asymptotics:
()
and since λɛ = k2(ɛ), we can derive the following formulas for λi:
()
Rewriting as a Taylor series with respect to ɛ, we have
()
Substituting (4.16) in (4.13), using (4.14), and equating the terms with the same powers of ɛ, we get the following boundary condition for vi, i = 1,2, …:
()
where
()
Consider now the boundary conditions on small holes. Analogously,
()
Substituting the Taylor series for 𝒥0(k(ɛ)(1 − ɛξ2)) with respect to ɛ in the last formula, using (4.14), and equating the terms with the same powers of ɛ in equation uɛ = 0 on Γɛ, we get the following boundary condition for vi,   i = 1,2, …, on ∂B:
()
where fi are polynomials of power i with respect to ξ2 with coefficients which depend on (k0, k1, …, ki−1). The precise formula for fi can be derived for each fixed i. For example, we have that
()
The following Lemma is useful for our analysis. For the proof see for example,[3].

Lemma 4.1. Suppose that F and v satisfy the conditions of Lemma 3.2. (a) If F is even with respect to ξ1, then v is even; (b) if F is odd with respect to ξ1 and A1 = A2 = 0, then v is odd with respect to ξ1 and decays exponentially as ξ2 → ∞.

Theorem 4.2. There exist numbers ki and π-periodic in ξ1 functions vi with finite Dirichlet integral in Π and exponential decay as ξ2 → ∞, such that these functions are solutions of the following boundary-value problems:

()
Moreover, the constants are defined by the formula:
()
In particular,
()
()

Proof. Let v be the solution of boundary-value problem (3.15). It can be easily verified that

()
is a solution of (4.22), (4.20), (4.17) for f1, g1, and k1 defined by (4.21), (4.18), and (4.24). For any k2 boundary-value problem (4.22), (4.20), (4.17) for v2 has a π-periodic solution with finite Dirichlet integral. By Lemma 3.2 and (3.27), v2 has exponential decay as ξ2 → ∞ if and only if k2 is given by (4.23) for i = 2. Let us verify formula (4.25) without applying the general (4.23). It is obvious that
()
By using that fact one can write the boundary-value problem for v2 as
()
It can be verified that the function
()
is π-periodic with finite Dirichlet integral in Π, has exponential decay as ξ2 → ∞, and satisfies problem (4.28) for k2 defined by (4.25). We can use the induction process to finalize the proof.

Since ki are defined by (4.23), we can calculate λi by using (4.15). Denote
()
where λɛ,N and vɛ,N are the partial sums of (2.4) and (4.3), respectively.

Theorem 4.2 implies the validity of the following useful result.

Theorem 4.3. For any integer N > 0, the function uɛ,N is the solution of the boundary-value problem

()
where , and N1 → ∞ as N → ∞.

Proof. According to the definition of uɛ,N, we have that

()
where
()
Passing from (x1, x2) variables to polar coordinates (r, θ), we get that
()
()

By using the fact that lim x→∞xe−αx = 0 and due to the result of Theorem 4.2, we have that, for any 1 ≤ i ≤ N,

()
where m is fixed. Hence, vɛ,N = O(ɛN+m). Similarly, taking into account (4.34) and (4.35), we can deduce that
()
Consequently,
()
Furthermore,
()

According to the definition of χ, the support of ∇xχ and Δxχ is the set {1/4 ≤ r ≤ 1/2}. Summarizing, we have that

()
and we can derive that
()
Therefore,
()
Consider now uɛ,N on Γɛ:
()
where βj are the coefficients of the Taylor series of the function . Hence, aɛ,N = O(ɛN+1) and
()
which yields that as N → ∞. Analogously, one can verify that as N → ∞. The proof is complete.

5. Complete Expansion in the Case of Multiple Eigenvalue λ0

In this section we consider the case when λ0 is of multiplicity two. The asymptotics of the eigenvalue were constructed in the form (2.4) and
()
()
()
In this case,
()
where are polynomials of power i with respect to ξ2 with coefficients which depend on (k0, k1, …, ki−1). Moreover,
()
where
()
()
Substituting (5.3) and (2.4) in (4.5), passing to the variables ξ and (θ, ρ), and collecting all the terms with equal order of ɛ, we get two systems of equations for and :
()
()

Theorem 5.1. There exist numbers ki and π-periodic in ξ1 even functions and odd functions with finite Dirichlet integral in Π, which have exponential decay as ξ2 → ∞, such that these functions are solutions of the boundary-value problems (5.8), (5.4), (5.5), and (5.9), (5.7), respectively. Moreover, the constants ki are defined by the formula:

()

Proof. The problems (5.8), (5.5), (5.4) for functions coincide with problems (4.22), (4.17), and (4.20) (if one change by and fi, gi by the respective ). Therefore the construction of and k1, k2 is just the same as the construction from the proof of Theorem 4.2. Due to (5.9), (5.7), the problem for is as follows:

()
The function is even (due to (4.26)) and, hence, the right-hand side is odd in (5.11) and is even in (5.8). By Lemma 3.2 and Theorem 4.2, we conclude that there exists the even solution of (5.11) with exponential decay. Then we can use the iteration process to complete the proof.

Denote
()
where λɛ,N and vɛ,N are the partial sums of (2.4) and (5.3), respectively.

Theorem 5.1 implies the validity of the following result.

Theorem 5.2. For any integer N > 0, the function uɛ,N is the solution of the boundary-value problem:

()
where , and N1 → ∞ as N → ∞.

Proof. The proof is analogous to the proof of Theorem 4.3. Hence, we omit the details.

6. Verification of the Asymptotics

Consider the boundary-value problem:
()
where F ∈ L2(Ω) and λ ≠ λ0 is some fixed number.
Similarly to the techniques used in [3, 18], one can show that the boundary-value problem (6.1) has the solution Uɛ ∈ H1(Ω) and the following representation holds:
()
for λ close to the simple eigenvalue λ0 of the problem (2.3) and
()
for λ close to multiple eigenvalue λ0 of the problem (2.3). Here uɛ is normalized in L2(Ω) eigenfunctions to (2.2) and is orthonormalized in L2(Ω) eigenfunctions to (2.2). Moreover,
()
where the constant C is independent on ɛ and λ. It follows from (6.2) and (6.4) that
()
Consider now the case of simple λ0. Define the function:
()
where uɛ,N and v are the solutions of (4.31) and (3.15), respectively, and C(B) is given by (3.18). Then, by Theorem 4.3, is the solution of (6.1) if
()
Taking into account (6.5), (6.7), and the fact that , we can conclude that for each fixed N,
()
Therefore the asymptotics constructed in Section 4 coincide with the expansion of λɛ. For the case of multiple λ0, one can use the same technique. The difference is follows: one should use (6.3) instead of (6.2) and Theorem 5.2 instead of Theorem 4.3. The asymptotics of λɛ are completely verified.

7. Application to a Friedrichs-Type Inequality

Consider the sets Ωɛ, Γɛ, which were defined in Section 2.

Definition 7.1. The Sobolev class H1(Ωɛ, Γɛ) is the class of functions from H1(Ωɛ) having zero trace on Γɛ.

Theorem 7.2. Let u ∈ H1(Ωɛ, Γɛ). Then a Friedrichs-type inequality

()
holds, where the best constant Kɛ has the asymptotics
()
as ɛ → 0. Here k0 is the smallest root of the Bessel function 𝒥0 and the constant C(B) is given by (3.18).

Proof. The geometric approach developed in [5, 9] allows us to state that there is a constant K > 0 such that

()
The idea and method of proof are exactly similar to the ones which were used in the mentioned papers. We are interested in the behavior of the best possible constant as ɛ → 0. Clearly, the best constant , where is the smallest eigenvalue of the boundary-value problem (2.2) (due to the variational formulation of the smallest eigenvalue). Therefore, we can apply (2.4) and (3.28) to derive the asymptotic expansion for Kɛ:
()
Since we are interested in the smallest eigenvalue , we have to choose the smallest positive root of 𝒥0(k0) = 0 as k0, precisely, k0 = 2,405. Then, we get, after some simple calculations and using (4.15) and (3.28),
()
The proof is complete.

Acknowledgments

This paper was completed during the stay of the second author as PostDoc at Luleå University of Technology in 2010-2011. The second author wants to express many thanks to Luleå University of Technology (Sweden) for financial support and wonderful conditions to work. The work of the first and the second authors was supported in part by RFBR (Project no. 09-01-00353) and the work of the forth author was supported by a grant from the Swedish Research Council (Project no. 621-2008-5186). The authors also thank referee for several suggestions, which have improved the final version of this paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.