International Journal of Differential Equations
Volume 2011, Issue 1 603183
Research Article
Open Access

Role of Delay on Planktonic Ecosystem in the Presence of a Toxic Producing Phytoplankton

Swati Khare, 

Corresponding Author

Swati Khare

School of Mathematics and Allied Sciences, Jiwaji University, MP Gwalior 474011, India jiwaji.edu

Search for more papers by this author
O. P. Misra, 

O. P. Misra

School of Mathematics and Allied Sciences, Jiwaji University, MP Gwalior 474011, India jiwaji.edu

Search for more papers by this author
Chhatrapal Singh, 

Chhatrapal Singh

School of Mathematics and Allied Sciences, Jiwaji University, MP Gwalior 474011, India jiwaji.edu

Search for more papers by this author
Joydip Dhar, 

Joydip Dhar

Department of Applied Sciences, ABV-Indian Institute of Information Technology and Management, MP Gwalior 474010, India iiitm.ac.in

Search for more papers by this author
First published: 11 October 2011
https://doi.org/10.1155/2011/603183
Citations: 10
Academic Editor: Gershon Wolansky

Abstract

A mathematical model is proposed to study the role of distributed delay on plankton ecosystem in the presence of a toxic producing phytoplankton. The model includes three state variables, namely, nutrient concentration, phytoplankton biomass, and zooplankton biomass. The release of toxic substance by phytoplankton species reduces the growth of zooplankton and this plays an important role in plankton dynamics. In this paper, we introduce a delay (time-lag) in the digestion of nutrient by phytoplankton. The stability analysis of all the feasible equilibria are studied and the existence of Hopf-bifurcation for the interior equilibrium of the system is explored. From the above analysis, we observe that the supply rate of nutrient and delay parameter play important role in changing the dynamical behaviour of the underlying system. Further, we have derived the explicit algorithm which determines the direction and the stability of Hopf-bifurcation solution. Finally, numerical simulation is carried out to support the theoretical result.

1. Introduction

The study of plankton system is an important area of research in marine ecology. Phytoplankton perform great service for earth. They provide food for marine life, oxygen for human being and also absorb half of the carbon dioxide which may be contributing to the global warming [1]. The dynamics of rapid (massive) increase or almost equal decrease of phytoplankton population is a common feature in marine plankton ecology and known as bloom. Blooms of red tide produce chemical toxin, a type of paralytic poison which can be harmful to zooplankton, fin fish, shellfish, fish, birds, marine mammals, and humans also. Some species, such as the dinoflagellate Alexandrium tamarense and the diatom Pseudo-nitzschia australis [2] produce potent toxins which are liberated into the water before they are eaten, and they may well affect zooplankton when they are in water. It is now well established that a significant number of phytoplankton species produce toxin, such as Pseudo-nitzschia, Gambierdiscus toxicus, Prorocentrum, Ostrepsis, Coolia monotis, Thecadinium, Amphidinium carterae, Dinophysis, Gymnodinium breve, Alexandrium, Gymodinium catenatum, Pyrodinium bahamense, Pfiesteria piscicida, Chrysochromulina polylepis, Prymnesium patelliferum, and P. parvum [3, 4]. Reduction of grazing pressure due to toxin is an important phenomena in plankton ecology [5, 6]. In aquatic system, toxin-producing phytoplankton may act as controlling factor in the phytoplankton-zooplankton interaction dynamics. Efforts have been made to study the role of toxin producing phytoplankton on the phytoplankton-zooplankton dynamics [7–9]. Toxicity may be the strong mediator of zooplankton feeding rate as shown by field studies [4, 10] and laboratory study [11].

Many researchers have been showing keen interest to investigate the direction and stability of Hopf-bifurcation of the system as refer their in [12, 13].

Our current study is motivated by [7, 8, 14], who have considered nutrient interaction with phytoplankton, phytoplankton interaction with zooplankton. The study of interacting species system with nutrient cycling which contributes to the growth of nutrient is carried out in [9, 14, 15]. A model can be more realistic if a delay effect (or time-lag) is being considered in the conversion from one species to another species [15–17]. The prey-predator systems with time delay are deeply considered by [18, 19] and many researchers have used distributed delay in their models [15, 16].

2. Mathematical Model Formulation

Let N(t) denote the concentration of nutrient at time t, x(t) denotes the biomass of toxic producing phytoplankton in the habitat that are partially harmful to zooplankton biomass, y(t). We assume a constant supply rate of nutrient (i.e., N0) in the system. The loss of nutrient due to leaching is assumed to be given by the term aN. We take a1 as the growth rate of phytoplankton biomass, w as the rate of predation of phytoplankton by zooplankton, and w1 denotes the corresponding conversion rate of zooplankton. The phytoplankton and zooplankton interaction is assumed to follow the Holling type-II functional response [20, 21] with D as half saturation constant. Again, the specific rate of nutrient uptake by per unit biomass of phytoplankton in unit time is considered to be bN and depletion of zooplankton biomass due to toxin-producing phytoplankton is given by the term c1xy. We further assume that phytoplankton and zooplankton biomass deplete due to natural mortality at the rate of b1 and a2, respectively, and k is the fraction of dead phytoplankton biomass that is being recycled back to the nutrient pool. With these assumption and notations, the resultant dynamics of the system under consideration is given by the following set of differential equations [14]:
()
with nonnegative initial conditions N(0), x(0), y(0) > 0. The above system of equations can be nondimensionalised using the relations x1 = N/D, x2 = x/D, x3 = y/D, τ = at, and introducing the new parameters α = N0/aD, β = bD/a, γ = b1/a, β1 = a1D/a, μ = w/a, μ1 = w1/a, ξ = a2/a, and ξ1 = c1D/a. The non-dimensionalised equations of the above system (2.1) are as follows in which we have replaced τ by t and get
()
with initial conditions: x1(0) > 0,   x2(0) > 0,   x3(0) > 0, where, α, β, γ, β1, μ, μ1, ξ, ξ1, and 0 < k < 1 are positive constants.
In this paper, our mathematical model is an extension of the system (2.2) which is studied earlier [14]. Now, we have introduced distributed delay in the digestion of nutrient by phytoplankton. The system (2.2) can be written as
()
where f(s) = f(x1) = x1(s), α1 is delay parameter,
()
putting
()
The above system of delay differential equation can be written as
()
with the additional initial condition: R(0) > 0.

3. Boundedness and Equilibria of the System

In this section, we will establish that the system (2.6) is bounded. We begin with the following lemma.

Lemma 3.1. The system (2.6) is uniformly bounded in Ω1, where

()
η1 = min {(1 − α), γ(1 − kβ1/β), ξ, α1}.

Proof. Let us consider a time dependent function:

()
Clearly,
()
Using (2.6) in the above expression we obtain
()
where η1 is chosen as the minimum of {(1 − α1), γ(1 − kβ1/β), ξ, α1}. Thus,
()
Now applying the theorem of differential inequalities [22], we obtain
()
as t → ∞, R → x1, which gives
()
Hence the solution of the system (2.6) is bounded in Ω1.

We now consider the existence of possible equilibria of the system (2.6). The system of (2.6) has three feasible equilibria, namely,
  • (i)

    boundary equilibrium: E1 ≡ (α, 0,0, α),

  • (ii)

    boundary equilibrium: E2 ≡ (γ/β1, (αβ1 − γ)/(β − kβ1)γ, 0, γ/β1). The boundary equilibrium E2 exists if either γ/α < β1 < β/k or β/k < β1 < γ/α is satisfied, that is, growth rate of phytoplankton biomass lies between the fraction of natural death rate of phytoplankton biomass to constant supply rate of nutrient and the fraction of nutrient uptake by phytoplankton biomass to fraction of dead phytoplankton biomass,

  • (iii)

    positive interior equilibrium: , where

    ()
    The positive interior equilibrium E3 exists if μ1 > ξ + ξ1, that is, the growth rate of zooplankton biomass is greater than the sum of natural death rate and death due to harmful phytoplankton, and also if means that concentration of nutrient at equilibrium is greater than the fraction of natural death rate of phytoplankton biomass to the depletion rate of nutrient uptake by phytoplankton biomass.

4. Dynamic Behaviour and Hopf-Bifurcation

In the previous section we observed that the system of (2.6) have three equilibria, namely, E1(α, 0,0, α), E2(γ/β, (αβ1 − γ)/(β − kβ1)γ, 0, γ/β), and . We will now examine the dynamical behaviour of the system about all the feasible equilibria.

The variational matrix for the system of (2.6) evaluated at E1 is
()

The eigenvalues of the characteristic equation of V1 are λ1 = −1, λ2 = (αβ1 − γ), λ3 = −ξ, and λ4 = −α1. It is seen from these eigenvalues that the equilibrium E1 is locally asymptotically stable if β1 < γ/α, which means that the growth rate of phytoplankton due to the availability of nutrient is less than the fraction of natural death rate of phytoplankton biomass to the constant input rate of nutrient.

The variational matrix for the system of (2.6) evaluated about E2 is
()
where
()
The eigenvalues λ1, λ2, and λ3 of the above matrix are the roots of the following cubic equation:
()
and the fourth eigenvalue is given by λ4 = j33.

Clearly, λ1, λ2, and λ3 have negative real parts if (αβ − kγ)(β − kβ1) > 0, β1 > γ/α, that is, growth rate of phytoplankton biomass is greater then the fraction of natural death rate of phytoplankton biomass to constant supply rate of nutrient and are satisfied, the eigenvalue λ4 is negative when . Thus, we can state the following theorem.

Theorem 4.1. The second boundary equilibrium E2 is linearly asymptotically stable if

()
are satisfied.

For the sake of convenience, the equilibrium points of the system is shifted to new points (n1, n2, n3, n4) through transformations , , , n4 = R − R*.

In terms of the new variables, the dynamical equations (2.6) can be written as in matrix form as
()
where dot(·) cover X denotes the derivative with respect to time. Here AX is the linear part of the system and B represents the nonlinear part. Moreover,
()
The eigenvalues of the matrix A help to understand the stability of the system. The characteristic equation for the variational matrix A is given by
()
where
()
Using the Routh-Hurwitz criteria [21, 23], we derive that the equilibrium E3 is locally asymptotically stable, if A1 > 0, A3 > 0, A1A2 > A3, and . Here the conditions A1 > 0, A3 > 0, A1A2 > A3, and requires
()
where , , , r4 = p2p3g2α1, , , , L4 = L1 + p1g2α1.

Thus, we can state the following theorem.

Theorem 4.2. The interior equilibrium E3 if it exists is linearly asymptotically stable when

()
are satisfied.

Now, we will study the Hopf-bifurcation [24, 25] of the system given by (2.6), taking α (i.e., constant input rate of nutrient) as the bifurcation parameter. The necessary and sufficient conditions for the existence of the Hopf-bifurcation for α = α*, if it exists, are (i) Ai(α*) > 0, i = 1,2, 3,4 (ii) A1(α*)A2(α*) > A3(α*) (iii) , and (iv) the eigenvalues of the characteristic equation (4.8) should be of the form λi = ui + ivi, where dui/dα ≠ 0, i = 1,2, 3,4. The condition becomes
()
where G1 = h1 + f1, , G3 = h3 − 2q5q6 − f3, , , , , , h1 = l2q5, h2 = l1q5 − l2q6, h3 = l1q6 + l3q5, h4 = l3q6, q1 = p1 − k2g6, q2 = k2g5, q3 = (p2k6 − p1k2)g5, q4 = (p2k6 − p1k2)g6 + g2α1, , , q7 = p2g2α1k6g5, q8 = p2k6g2α1g6, , g3 = 1/g2, g4 = g1/g2, , , , . Therefore, one pair of eigenvalues of the characteristic equation (4.8) at α = α* are of the form λ1,2 = ±iv, where v is positive real number.
Now, we will verify the Hopf-bifurcation condition (iv), putting λ = u + iv in (4.8), we get
()
On separating the real and imaginary parts and eliminating v between real and imaginary parts, we have
()
()
Substituting the value of v2 from (4.15) in (4.14), we get
()
differentiating with respect to α and putting α = α*,we have
()
Hence we can state the following theorem.

Theorem 4.3. The system (2.6) has a Hopf-bifurcation at α* > 0 such that

()

At the Hopf-bifurcation point, the equilibrium state loses its stability and bifurcates to a periodic orbit. We obtain the value of α at the Hopf-bifurcation point denoted as α* and solve the equation
()
At the Hopf-bifurcation point, where the real parts of complex conjugate eigenvalues are zero, the roots of (4.8) are
()
where , , and .
Next, we seek a transformation matrix P which reduces the matrix A to the form
()
where the nonsingular matrix P is given as
()
where, a11 = v2c − edα1 − α1v, a12 = α1vc + v3 + edω, , , , , , , a41 = (ω2 + ed)α1, a42 = vcα1, , , , , .

To achieve the normal form of (4.6), we make another change of variable, that is, X = PY, where .

Through some algebraic manipulations, (4.6) takes the form
()
where Ω = P−1AP and
()
where, f1(y1, y2, y3, y4) = −β(a11y1 + a12y2 + a13y3 + a14y4)(a22y2 + a23y3 + a24y4), f2(y1, y2, y3, y4) = −μp4(a22y2 + a23y3 + a24y4)(a31y1 + a31y3 + a31y4)+(a22y2 + a23y3 + a24y4)(a41y1 + a42y2 + a43y3 + a44y4)β1 + p2p4(a22y2 + a23y3 + a24y4), f3(y1, y2, y3, y4) = −p2p4(a22y2 + a23y3+a24y4)(a31y1 + a31y3+a23y3 + a24y4) 2(a31y1+a31y3 + a31y4)−(a22y2 + a23y3 + a24y4)(a31y1 + a31y3 + a31y4)ξ1, f4(y1, y2, y3, y4) = 0.
Equation (4.23) is the normal form of (4.6) from which the stability coefficient can be computed. In (4.6), on the right hand side the first term is linear and the second one is nonlinear in y’s. For evaluating the direction of bifurcating solution, we can evaluate the following quantities at α = α* and origin
()
()
()
()
()
Thus, we can determine g11, g20, g02, g21 from (4.25), (4.26), (4.27), and (4.29), respectively. Thus, we can compute the following values:
()
which determine the qualities of bifurcation periodic solution in the center manifold at the critical value α*.

Theorem 4.4. The parameter μ2 determines the direction of the Hopf-bifurcation if μ2 > 0  (μ2 < 0), then the Hopf-bifurcation is supercritical (subcritical) and the bifurcation periodic solutions exist for α > α*(α > α*); β2 determines the stability of bifurcating periodic solution; the bifurcation periodic solutions are orbitally asymptotically stable (unstable) if β2 < 0  (β2 > 0); τ2 determines the periodic of the bifurcating periodic solution; the period increases (decreases) if τ2 > 0  (τ2 < 0).

5. Numerical Example

In this section, we have performed numerical simulation for both systems (2.2) as well as (2.6) using MATLAB. We are taking parametric values β = 0.3,   γ = 0.2,   k = 0.3,   β1 = 0.25,   μ = 0.2,   μ1 = 0.19,   ξ = 0.05,   ξ1 = 0.01 for both systems. The behavior of the system (2.2) with different values of α. From Figures 1, 2, 3, 4, it is observed that as α increases, the stable system starts oscillating. Again, with these set of values and α1 = 0.12, we get a positive root of (4.12) is α = α* = 1.1680. Therefore, one pair of eigenvalues of the characteristic equation (4.8) at α = α* = 1.1680 are of the form λ1,2 = ±iv, where v is positive real number. Here the positive interior equilibrium is E3(1.06505,0.3967,0.462745). It follows from Section 4, Theorem 4.3, that α* = 1.1680, the positive equilibrium E3 is stable when α < α* (see Figure 7) and the system (2.6) undergoes a Hopf-bifurcation at α > α* (see Figure 8). Now keeping α = 1.1, further reduction of α1 at 0.01 and 0.07 are shown on Figures 5-6. Moreover, we can determine the stability and direction of periodic bifurcation from the positive equilibrium at the critical point α*. For instance, when α = α* = 1.1680, g11 = −0.0000105695 − 0.0000200596i, g20 = 0.0000362402 − 5.6110710−6i, g02 = −0.0000151012 + 0.0000457302i, g21 = −6.90210−8 − 4.0204810−8i, C1(0) = −4.0826910−8 + 1.6292810−9i, u′(α*) = 0.00115975. It follows from (4.30) that μ2 > 0 and β2 < 0. Therefore, the bifurcation takes place when α crosses α* to the right (α > α*), and the corresponding periodic orbits are orbitally asymptotically stable, as depicted in Figure 8.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.1775.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Stable phase-space diagram for the system with nutrient, phytoplankton, and zooplankton at α = 1.25.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.3.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.1, α1 = 0.01.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.1, α1 = 0.07.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Stable phase-space diagram for the system with nutrient, phytoplankton, and zooplankton at α = 1.1, α1 = 0.12.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Phase-space diagram for nutrient, phytoplankton, and zooplankton at α = 1.1775, α1 = 0.12.

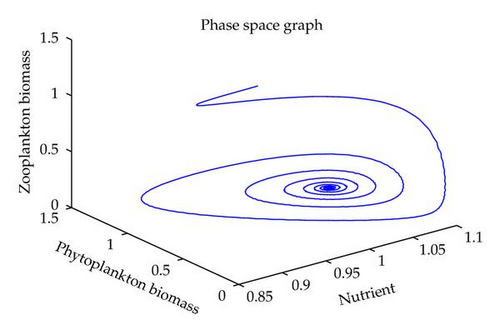
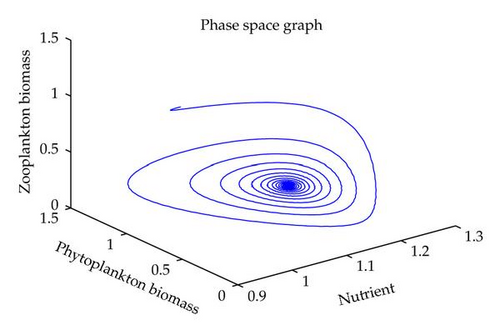
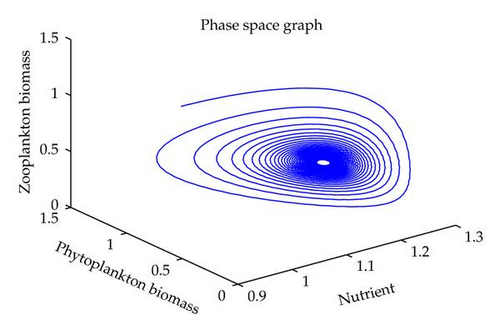
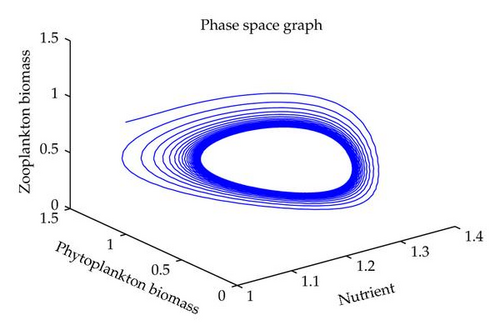
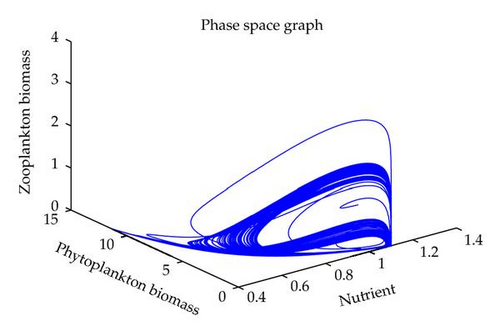
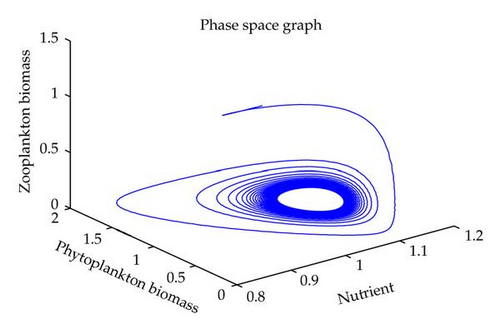
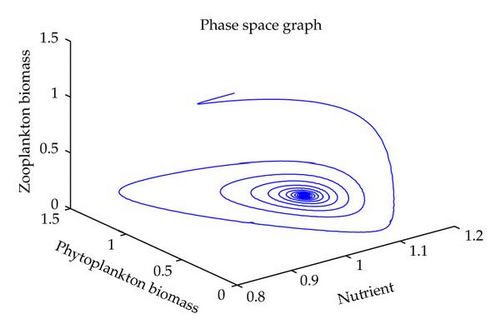
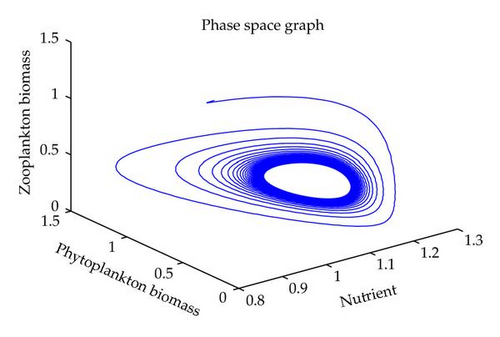
6. Conclusion

In this paper, we have studied the role of delay on plankton ecosystem in the presence of a toxic producing phytoplankton. In this system, it has been assumed that the toxic phytoplankton reduces the growth of zooplankton and studied the effect of delay in the digestion of nutrient by phytoplankton biomass. The local stability conditions of all the feasible equilibria of the system are established. The interior equilibrium are locally asymptotically stable under certain conditions. We have shown numerically with the set of parameters that at α1 = 0.01, the system exhibits the chaotic behavior (see Figure 5). Figure 6 exhibits the oscillatory behavior of the system and further it is observed that the increase in α1 makes the system stable (see Figure 7). For the comparison of the system (2.6), without delay in the system, a numerical simulation of the system (2.2) is shown in Figures 1, 2, 3, 4. By applying the normal form theory and the center manifold theorem, we define the explicit formulae that determine the stability and direction of the bifurcating periodic solutions. For numerical experiment, it is observed that when the input rate of nutrient, α, exceeds the critical value α*(1.1680), the system (2.6) leads to oscillatory behaviour shown in Figure 8. Thus, the quantitative level of abundance of system populations depends crucially on the input rate of nutrient. Further from Theorem 4.4, we can determine the direction and stability of Hopf-bifurcation. For these chosen set of parametric values, the Hopf-bifurcation is supercritical and stable. Hence, we conclude that the supply rate (α) of nutrient and delay parameter (α1) play an important role in changing the dynamical behaviour of the system.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.