Volume 2011, Issue 1 561592

Research Article

Open Access

Optimization of a Pumped-Storage Fixed-Head Hydroplant: The Bang-Singular-Bang Solution

L. Bayón,

Corresponding Author

L. Bayón

[email protected]

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

J. M. Grau,

J. M. Grau

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

M. M. Ruiz,

M. M. Ruiz

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

P. M. Suárez,

P. M. Suárez

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

L. Bayón,

Corresponding Author

L. Bayón

[email protected]

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

J. M. Grau,

J. M. Grau

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

M. M. Ruiz,

M. M. Ruiz

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

P. M. Suárez,

P. M. Suárez

Department of Mathematics, University of Oviedo, E.P.I. Campus of Viesques, 33203 Gijón, Spain uniovi.es

Search for more papers by this author

First published: 09 August 2011

https://doi.org/10.1155/2011/561592

Citations: 2

Academic Editor: Horst Ecker

Share a link

Email
Wechat
Bluesky

Abstract

We consider the problem of the optimization of the functioning of a pumped-storage hydroplant. The problem can be mathematically formulated as an optimal control problem, and when the considered hydromodel is of the fixed-head type, an added complication arises: the solution is of the bangsingular-bang type. In this paper, we propose a simple and efficient optimization algorithm to find the solution.

1. Introduction

This paper has a clear aim: optimizing the functioning of a pumped-storage hydroplant, with the context of the decentralized Spanish electricity market [1].

In the literature (see [2, 3]), numerous simplifications are performed to model plants of this kind, in order to obtain an extremely simple mathematical formulation which permits the use of commercial packages of, for instance, linear programming. Readers are referred to [4], which constitutes an excellent list of over 100 of relevant research papers on the hydroplant modeling.

However, the optimization of pumped-storage hydroplants is a complex Dynamic Programming problem [5], with given time and final state. The problem can be mathematically formulated as a standard Lagrange-type optimal control problem [6]. In a previous paper [7] the authors considered a variable-head model for the pumped-storage hydroplant. The solution can be obtained using Pontryagin’s Maximum Principle [5]. In another previous paper [8] the authors considered a fixed-head model for a conventional hydroplant, without pumping capacity. The solution is of the bang-bang type, and the absence of singular arcs was proven. However, when the considered model is fixed head and pumped storage simultaneously, an added complication arises: the solution is of the bang-singular-bang type.

Different methods for determining optimal controls with a possibly singular part have already been developed. A popular approach introduced by Jacobson et al. [9] has been used by a number of researchers including Edgar and Lapidus [10, 11] and more recently by Chen and Huang [12]. This method involves solving the singular/bang-bang optimal control problem as the limit of a series of nonsingular problems. It is important to establish the limitations of these perturbation-based methods for practical problems. In fact, the convergence criterion described in [9] requires that the perturbation parameter, ε, be sufficiently small; however, numerical difficulties result when ε approaches a zero limit. The reader is referred to [12–14] for further details. Maurer et al. [15] presented a numerical scheme for computing optimal bang-bang controls. They assume that every component of the optimal control is bang-bang and that there are only a known finite number of switching times. Assuming that the optimal control structure is known, [16] formulates a new finite-dimensional optimization problem involving the initial states, the switching times, and the final time t_f as optimization variables. Another idea is to guess a possible control structure and start with some additional bang-bang and singular arcs. The optimization approach will then lead to a solution where the lengths of all redundant arcs will be optimized to zero. Alternatively, the direct monotone structural evolution method [17] additionally takes advantage of the minimum principle optimality conditions to obtain the correct control structure. For the study of sufficient conditions, the reader is referred, for example, to [18, 19].

Faced with the existence of diverse general methods for bang-singular-bang problems, in this paper we have developed a specific algorithm for our problem. Our method needs no prior knowledge of the number and location of the bang-singular-bang arcs neither does it handle any parameter (like, e.g., discretization or a penalization factor) that has an influence on convergence or the precision of the result.

In this paper we propose a simple and efficient optimization algorithm to find the bang-singular-bang solution to our hydroproblem. Though we treat only a specific hydraulic problem, it should be noted that our method may be applied to other problems with the same characteristics. The paper is organized in the following way. In Section 2 we set out the corresponding mathematical problem. Section 3 summarizes the optimization algorithm based upon the previous mathematical fundaments. Finally, the results obtained in an example are presented in Section 4, and the conclusions reached in this study are discussed in Section 5.

2. Mathematical Optimization of a Pumped-Storage Hydroplant

A basic physicallybased relationship between the active power generated by a hydroplant, P (in MW), the rate of water discharge, z^′ (in m³/s), and the effective head, h (in m), is given by

(2.1)

where G is the efficiency (in m⁴/h·MW) (see [20, 21]). For a large capacity reservoir, it is practical to assume that the effective head is constant over the optimization interval. Here the fixed-head hydroplant model is defined and P is represented by the linear equation:

(2.2)

where A represents the efficiency and diverse parameters related to the geometry of the station (see [20] for further details). Pumped-storage is a well-known type of hydroplants used for load balancing. The method stores energy in the form of water, which is pumped from a lower to an upper reservoir. At times of low electrical demand, electric power is used to pump water into the upper reservoir. During periods of high electrical demand, water is released back into the lower reservoir through a turbine, thereby generating electricity.

Taking into account the conversion losses of the pumping process and evaporation losses from the exposed water surface, a maximum of 70% or 85% of the electrical energy used to pump the water into the elevated reservoir can be regained. Thus, we must introduce the efficiency, η, in the model. Despite these losses, when scheduling is optimized, the system increases revenue by selling more electricity during periods of peak demand, when electricity prices get higher. Hence, when pumped-storage plants are considered, the function P is defined piecewise as

(2.3)

If we assume that b is the volume of water that must be discharged throughout the optimization interval [0, T], the following boundary conditions will have to be fulfilled:

(2.4)

Besides the previous statement, we consider z^′(t) to be bounded by technical constraints

(2.5)

No transmission losses will be considered in our study. From the perspective of a generation company and within the framework of the new electricity market, said losses are not relevant, as power generators currently receive payment for all the energy they generate in power plant bars.

In this section, we focus on the new short-term problem faced by a generation company, in a deregulated electricity market, when preparing its offers for the day-ahead market. Our model of the spot market explicitly represents the price of electricity as a known exogenous variable.

In our problem, the objective function is given by hydraulic profit over the optimization interval, [0, T]. Profit is obtained by multiplying the hydraulic production of the pumped-storage hydroplant by the clearing price, π(t), at each hour, t. Taking our objective functional F(z) in continuous time form, the problem is

(2.6)

(2.7)

A standard Lagrange-type optimal control problem can be mathematically formulated as follows:

(2.8)

We define the Hamiltonian in normal form:

(2.9)

The resulting Hamiltonian, H, is linear in the control variable, u, and results in an optimal singular/bang-bang control policy. In general, the application of Pontryagin′s Maximum Principle [5] is not well suited for computing singular control problems as it fails to yield a unique value for the control. It is well known [6] that when the Hamiltonian is linear in u, the optimality condition (maximize H u) leads to

(2.10)

and u^* is undetermined if Φ(x, λ) ≡ H_u = 0. The function Φ is called the switching function. If Φ(x^*(t), λ(t)) = 0 only at isolated time points, then the optimal control switches between its upper and lower bounds, which is said to be a bang-bang-type control (i.e., the problem is not singular). The times when the OC switches from u_max to u_min or vice versa are called switching times. If Φ(x^*(t), λ(t)) = 0 for every t in some subinterval [t^′, t^′′] of [0, T], then the original problem is called a singular control problem and the corresponding trajectory for [t^′, t^′′], a singular arc. The case when Φ vanishes over an interval is more troublesome, because the optimality condition is vacuous.

In our problem, however, an added complication arises: the Hamiltonian is defined piecewisely as

(2.11)

and the derivative of H with respect to u (H_u) presents discontinuity at u = 0, which is the point at which a sudden change in H_u is produced, as it is the border between the power generation zone (positive values of u) and the pumping zone (negative values of u).

The classical gradient of H at u is defined only when H is differentiable at u. However, when nondifferentiable objective functions arise in optimization problems, the generalized (or Clarke′s) gradient (see [22, 23]) must be considered. Remember that the Clarke’s gradient, ∂f, can be calculated as a convex hull of (almost) all converging sequences of the gradients

(2.12)

With the aim of obtaining a numerical solution, we first attempt to determine the structure of the solution that is, the sequence of the bang-bang and the singular parts.

Bearing in mind that the function H_u(t, ·, λ) is discontinuous in u = 0, and that if u ≠ 0, then

, we have that the partial Clarke’s gradient is

(2.13)

with

and

. The switching function is Φ(z, λ) ≡ ∂_uH, and the optimality condition leads to

(2.14)

On the other hand, the costate equation of Pontryagin’s Maximum Principle allows us to obtain

(2.15)

With the previous mathematical development, we can determine the optimal solution: the bang-singular-bang segments and the boundary on which the solution is situated

(2.16)

3. Algorithm

Based on the above theoretical results, in this section we describe the optimization algorithm.

The algorithm presents a series of advantages. First of all, our method needs no prior knowledge of the number and location of the bang-singular-bang arcs. Moreover (as we will see in the next section), it shows a rapid convergence to the optimal solution, and it can be run in a relatively short time due to the simplicity of the operations to be performed in this method.

Figure 1 illustrates the switching law, which is in fact the basis for the proposed method. The algorithm that leads to the optimal solution comprises the following steps.

(i)
First, π(t) must be interpolated to obtain a continuous function.
(ii)
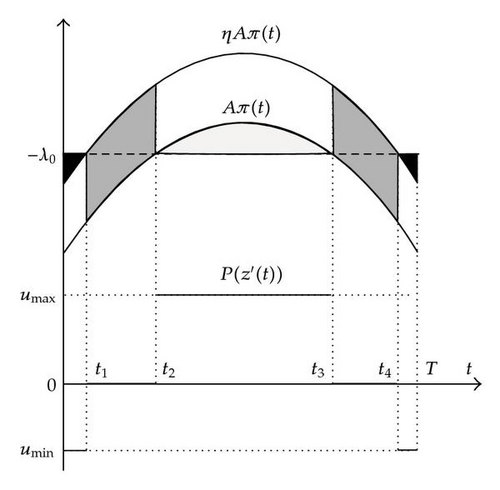
Second, for a given λ, we have to determine the switching times: t₁, t₂, …. These instants are calculated solving
(3.1)
(iii)
Third, the optimal value λ₀ must be determined in order for
(3.2)
with and being the duration of the ith bang-bang segment in the upper and lower bound, respectively, N_u and N_l the number of such segments, and z_λ(T) the final volume obtained for each λ.
(iv)
To calculate an approximate value of λ₀, we propose a classic iterative method (like, e.g., bisection or the secant method).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of the switching law.

In the next section the proposed method is applied to an example.

4. Example

A program was written using the Mathematica package to apply the results obtained in this paper to an example of a hydraulic system made up of one fixed-head hydroplant. The hydraulic model is

(4.1)

with A = 0.000126821. We shall also consider the technical constraints: q_min = −283866 (m³/h), q_max = 394258 (m³/h). When the efficiency is η = 1.15, these constraints, respectively, correspond to P_min = −41.4, P_max = 50 (MW).

In this paper, we focus on the problem that a generation company faces when preparing its offers for the day-ahead market. Thus, the classic optimization interval of T = 24 h. was considered. The clearing price, π(t) (euros/h·MW), corresponding to one day was taken from the Spanish electricity market [1] (see Table 1). Note that in real electricity markets, the clearing price, π(t), is only known at each hour (t = 1,2, …, 24). In this paper the known values of π(t) were linearly interpolated with good results.

Table 1. The clearing price, π(t).

t	π(t)	t	π(t)	t	π(t)	t	π(t)
1	76.93	7	69.47	13	104.08	19	90.00
2	68.20	8	75.79	14	100.00	20	106.89
3	68.20	9	105.90	15	80.50	21	103.00
4	60.00	10	106.50	16	78.23	22	100.00
5	55.01	11	110.00	17	75.93	23	86.93
6	56.28	12	108.46	18	78.23	24	79.93

The solution may be constructed in a simple way by taking into account the above algorithm. We shall perform two tests.

4.1. Influence of the Efficiency

First, we consider the restriction on the volume: b = 2 · 10⁶ (m³) as a fixed datum and then we proceed to analyze the influence of the efficiency, η. In Table 2 we present the optimal profit when the efficiency falls within the 1.35 to 1.15 range. We show the amount of pumped water and the improvement in profit with respect to the case without pumping.

Table 2. Optimal solution varying η.

η	Profit (euros)	Pumped water (m³)	% improvement
without pumping	27145.2	0	0
1.35	30282.5	1.49123 · 10⁶	11.6
1.30	30896.4	1.61463 · 10⁶	13.8
1.25	31567.5	1.7438 · 10⁶	16.3
1.20	32300.	1.87975 · 10⁶	18.9
1.15	33105.5	2.07863 · 10⁶	21.9

Table 3. Optimal solution varying b.

b (m³)	Profit (euros)	Profit (euros)	% improvement
b (m³)	(without pumping)	(with pumping)	% improvement
1 · 10⁶	13753.1	20633.9	50.0
2 · 10⁶	27145.2	32300	18.9
3 · 10⁶	40067.6	43318.3	8.1
4 · 10⁶	52017.6	53733.1	3.3

As can be appreciated, significant improvements in profit of between 12–14% are obtained for even very poor efficiencies (in the 65–75% range). For the normal efficiency of pumped plants of around 80%, the improvement in profit is quite substantial, being around 20%.

In Figure 2 we present the solution of the algorithm when the efficiency is η = 1.20. The optimal value obtained for −λ₀ is 0.01139601030789622, and the switching times are

(4.2)

Figure 3 presents the optimal hydro-power, P, for three cases: (a) without pumping, (b) with η = 1.2, and (c) with η = 1.15.

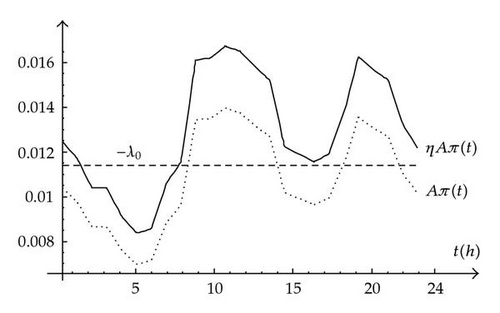
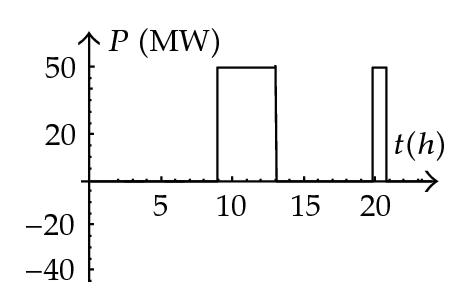
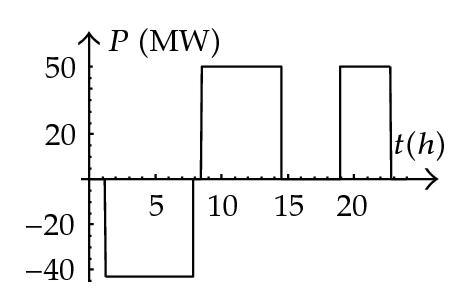
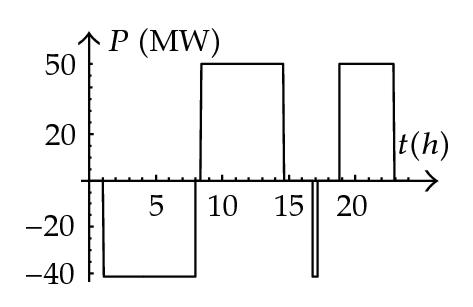
It can clearly be seen that when η = 1.2 (standard efficiency of 80%), the plant pumps during the most off-peak period in the clearing price π(t). However, when η = 1.15, and hence the efficiency increases to 85%, the plant also pumps in the small off-peak period in the clearing price π(t) that usually occurs around 17.00 h.

The singular arcs correspond to what, in a previous paper [24], we called a smooth transition. This is a qualitative aspect of the solution of the problem. The discontinuity of the derivative of the Lagrangian does not translate as discontinuity in the derivative of the solution. In fact, it is verified that the derivative of the extremal where the minimum is reached presents an interval of constancy.

The algorithm runs very quickly (see Figure 4). In case (b), with η = 1.2, 7 iterations were needed, with the CPU time required by the program being 1.1 sec on a personal computer (Pentium IV/2 GHz). The secant method was used to calculate the approximate value of λ for which

(4.3)

with tol = 50 (m³). The secant method has provided satisfactory results using these initial values:

(4.4)

4.2. Influence of the Volume Available

Second, we consider the efficiency η = 1.2 as a fixed datum, and then we proceed to analyze the influence of the restriction on the volume b. We compare with the solution without pumping.

As can be seen (see Table 1), the more the water available in the reservoir, the lower the profit obtained from pumping it. In fact, if the average flow of the river was such that volumes of water of 4 · 10⁶ (m³) were available, it would not be of interest to consider building a pump plant.

This type of study is very interesting when designing the most suitable type of plant for each hydrographic basin.

5. Conclusions

In this paper we have presented a simple and efficient optimization algorithm to optimize the functioning of a pumped-storage hydroplant. When the hydroplant is of the fixed-head type, the optimal solution presents a very particular form: the bang-singular-bang solution. Faced with the existence of diverse general methods for bang-singular-bang problems, in this paper we have developed a specific algorithm for our problem. Our algorithm allows the optimal solution to be obtained easily. The obtained results provide real-time information to determine which configuration is preferable in each specific real situation of the electricity market. Our theoretical results have been illustrated with numerical examples.

As to future perspectives, in spite of having presented a hydraulic example in this paper, it should be noted that our method may be applied to other problems with the same characteristics, with a constant value of the adjoint. Another interesting future line of study could be that of adapting the technique present in [19] to our hydraulic problem. In this paper the authors present an application to a free-flying robot, where it has been shown that the singular arc of the control can be interpreted as a bang-bang control of a so-called augmented smooth control problem.

Acknowledgment

This work was supported by the Spanish Government (MICINN, Project: MTM2010-15737).

References

1 Omel S. A., Electricity market activity rules, http://www.omel.es/files/EMRules_2.pdf.
Google Scholar
2 Jia J., Zhai Q., Guan X., Wu H., and Li Q., Optimal short term scheduling of cascaded hydroelectric chain plants with pumped-storage units, Proceedings of the 27th Chinese Control Conference (CCC ′08), July 2008, Kunming, China, 521–525, 2-s2.0-52449112365, https://doi.org/10.1109/CHICC.2008.4605215.
10.1109/CHICC.2008.4605215
Google Scholar
3 Brown P. D., Peças Lopes J. A., and Matos M. A., Optimization of pumped storage capacity in an isolated power system with large renewable penetration, IEEE Transactions on Power Systems. (2008) 23, no. 2, 523–531, 2-s2.0-43849089097, https://doi.org/10.1109/TPWRS.2008.919419.
10.1109/TPWRS.2008.919419
Web of Science® Google Scholar
4 Kishor N., Saini R. P., and Singh S. P., A review on hydropower plant models and control, Renewable and Sustainable Energy Reviews. (2007) 11, no. 5, 776–796, 2-s2.0-33751410643, https://doi.org/10.1016/j.rser.2005.06.003.
10.1016/j.rser.2005.06.003
Web of Science® Google Scholar
5 Bertsekas D. P., Dynamic Programming and Optimal Control, 2007, Athena Scientific.
Google Scholar
6 Vinter R., Optimal Control, 2000, Birkhäuser, Boston, Mass, USA, Systems & Control: Foundations & Applications, 1756410.
Google Scholar
7 Bayón L., Grau J. M., Ruiz M. M., and Suárez P. M., An optimization problem in deregulated electricity markets solved with the nonsmooth maximum principle, International Journal of Computer Mathematics. (2009) 86, no. 2, 237–249, 2488025, https://doi.org/10.1080/00207160701864483, ZBL1155.91441.
10.1080/00207160701864483
Web of Science® Google Scholar
8 Bayón L., Grau J. M., Ruiz M. M., and Suárez P. M., An algorithm for bang-bang control of fixed-head hydroplants, International Journal of Computer Mathematics. (2011) 88, no. 9, 1949–1959, https://doi.org/10.1080/00207160.2010.502934.
10.1080/00207160.2010.502934
Web of Science® Google Scholar
9 Jacobson D. H., Gershwin S. B., and Lele M. M., Computation of optimal singular controls, IEEE Transactions on Automatic Control. (1970) 15, 67–73, 0274135.
10.1109/TAC.1970.1099360
Web of Science® Google Scholar
10 Edgar T. F. and Lapidus L., The computation of optimal singular bang-bang control I: linear systems, AIChE Journal. (1972) 18, no. 4, 774–779, https://doi.org/10.1002/aic.690180419.
10.1002/aic.690180419
CAS Web of Science® Google Scholar
11 Edgar T. F. and Lapidus L., The computation of optimal singular bang-bang control II: nonlinear systems, AIChE Journal. (1972) 18, no. 4, 780–785, https://doi.org/10.1002/aic.690180420.
10.1002/aic.690180420
CAS Web of Science® Google Scholar
12 Chen Y. and Huang J., A continuation method for singular optimal control synthesis, Proceedings of the American Control Conference (ACC ′93), June 1993, San Francisco, Calif, USA, 1256–1260, 2-s2.0-0027846687.
Google Scholar
13 Dadebo S. A. and McAuley K. B., On the computation of optimal singular controls, Proceedings of the 4th IEEE Conference on Control Applications, September 1995, Albany, NY, USA, 150–155, https://doi.org/10.1109/CCA.1995.555659, 2-s2.0-0029517471.
10.1109/CCA.1995.555659
Google Scholar
14 Dadebo S. A., McAuley K. B., and McLellan P. J., On the computation of optimal singular and bang-bang controls, Optimal Control Applications & Methods. (1998) 19, no. 4, 287–297, 1650209, https://doi.org/10.1002/(SICI)1099-1514(199807/08)19:4<287::AID-OCA628>3.0.CO;2-S.
10.1002/(SICI)1099-1514(199807/08)19:4<287::AID-OCA628>3.0.CO;2-S
Web of Science® Google Scholar
15 Maurer H., Buskens C., Kim J. H. R., and Kaya C. Y., Optimization methods for the verification of second order sufficient conditions for bang-bang controls, Optimal Control Applications & Methods. (2005) 26, no. 3, 129–156, 2150512, https://doi.org/10.1002/oca.756.
10.1002/oca.756
Web of Science® Google Scholar
16 Vossen G., Switching time optimization for bang-bang and singular controls, Journal of Optimization: Theory and Applications. (2010) 144, no. 2, 409–429, 2581113, https://doi.org/10.1007/s10957-009-9594-4, ZBL1185.49022.
10.1007/s10957-009-9594-4
Web of Science® Google Scholar
17 Szymkat M. and Korytowski A., Method of monotone structural evolution for control and state constrained optimal control problems, Proceedings of the 7th European Control Conference (ECC ′03), September 2003, Cambridge, UK, University of Cambridge.
Google Scholar
18 Poggiolini L. and Stefani G., Minimum time optimality for a bang-singular arc: second order sufficient conditions, Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference (CDC-ECC ′05), December 2005, Seville, Spain, 1433–1438, 2-s2.0-33847226311, https://doi.org/10.1109/CDC.2005.1582360.
10.1109/CDC.2005.1582360
Google Scholar
19 Vossen G. and Maurer H., On L¹-minimization in optimal control and applications to robotics, Optimal Control Applications & Methods. (2006) 27, no. 6, 301–321, 2283487, https://doi.org/10.1002/oca.781.
10.1002/oca.781
Web of Science® Google Scholar
20 El-Hawary M. E. and Christensen G. S., Optimal Economic Operation of Electric Power Systems, 1979, 142, Academic Press, New York, NY, USA, Mathematics in Science and Engineering, 696769.
Google Scholar
21 Wood A. J. and Wollenberg B. F., Power Generation, Operation and Control, 2006, Wiley India Pvt, New Delhi, India.
Google Scholar
22 Clarke F. H., Optimization and Nonsmooth Analysis, 1983, John Wiley & Sons, New York, NY, USA, Canadian Mathematical Society Series of Monographs and Advanced Texts, 709590.
Google Scholar
23 Loewen P. D., Optimal Control via Nonsmooth Analysis, 1993, 2, American Mathematical Society, Providence, RI, USA, CRM Proceedings & Lecture Notes, 1232864.
10.1090/crmp/002
Google Scholar
24 Bayón L., Grau J. M., Ruiz M. M., and Suárez P. M., A constrained and non-smooth hydrothermal problem, Applied Mathematics and Computation. (2009) 209, no. 1, 10–18, 2493281, https://doi.org/10.1016/j.amc.2008.06.013, ZBL1187.80006.
10.1016/j.amc.2008.06.013
Web of Science® Google Scholar

Citing Literature

All articles

Optimization of a Pumped-Storage Fixed-Head Hydroplant: The Bang-Singular-Bang Solution

Abstract

1. Introduction

2. Mathematical Optimization of a Pumped-Storage Hydroplant

3. Algorithm

4. Example

4.1. Influence of the Efficiency

4.2. Influence of the Volume Available

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Optimization of a Pumped-Storage Fixed-Head Hydroplant: The Bang-Singular-Bang Solution

Abstract

1. Introduction

2. Mathematical Optimization of a Pumped-Storage Hydroplant

3. Algorithm

4. Example

4.1. Influence of the Efficiency

4.2. Influence of the Volume Available

5. Conclusions

Acknowledgment

References

Citing Literature

Figures

References

Related

Information