Millimeter-Wave Rotational Spectrum, Barrier to Internal Rotation, and DFT Calculation of o-Tolunitrile
Abstract
The millimeter-wave rotational spectra of o-tolunitrile (C6H4CH3CN) have been investigated in the ground torsional state in the frequency range 50.0–75.0 GHz. Many high-J rotational lines with large A-E splitting due to internal rotation of the methyl top have been assigned. A least squares analysis of the A-E splitting of 92 transitions resulted in the determination of accurate values of internal rotation parameters. The observed parameters were compared with the previously reported experimental values and DFT calculation results.
1. Introduction
The microwave rotational spectra of molecules having a methyl top attached to a planar frame shows a characteristic splitting corresponding to A and E symmetry of the torsional states. These A-E doublets may be closely or widely spaced depending on the height of the potential barrier and transitions studied. Hence, an analysis of the observed A-E splitting would lead to the determination of the barrier height hindering the internal rotation. Microwave spectroscopic techniques have been widely employed to study the effect of internal rotation of the methyl group on the rotational spectra of the molecules concerned.
Extensive studies on the microwave [1–5] and electronic [6–8] spectra of toluene and substituted toluenes have been reported in the literature. In contrast, not much microwave spectroscopic work has been reported on tolunitriles. Fujii et al. [9] have investigated the fluorescence excitation and dispersed fluorescence spectra of o-, m-, and p-tolunitrile in supersonic jets. By analyzing the low-frequency bands due to internal rotation of the methyl group they have successfully determined the height of the potential barrier hindering the internal rotation for m- and p-tolunitrile. However, in the case of o-tolunitrile, the absence of low-frequency bands prevented them from determining the potential barrier.
In an earlier communication, Jaman et al. [10] have reported the rotational constants and a value of the potential barrier V3 from an analysis of the A-E splitting of the microwave spectrum of o-tolunitrile in the ground torsional state. Later, Hansen et al [11] have investigated the high-resolution microwave spectrum of o-tolunitrile by using molecular beam FT microwave spectroscopic technique and determined rotational, centrifugal distortion constants, 14N nuclear quadrupole hyperfine constants, as well as V3. The internal rotation parameters reported in [10, 11] were in good agreement with each other.
In the present communication, we have extended the analysis of the microwave spectra of o-tolunitrile to high-J rotational transitions where the A-E splittings are large. The inclusion of high-J rotational transitions in the least-squares analysis has improved the accuracy of the molecular constants. Furthermore, a detailed DFT calculation on the molecular structure, molecular constants, and internal rotation parameters are reported and compared with the experimental values.
2. Experimental Details
The sample of o-tolunitrile was obtained from Aldrich Chemical Co. (quoted purity: 98%) and was used without further purification. The millimeterwave spectrum was observed and measured with a conventional 100 kHz Stark-modulated spectrometer in the frequency range 50.0–75.0 GHz. Okaya 24V10A and 35V10 klystrons followed by a frequency doubler (Millitech model MUD-15-H23FO) were used as frequency sources. The klystron frequency was swept by applying a sawtooth voltage on its repeller. The absorption line was modulated with a 100 kHz square wave and phase sensitively detected by using a lock-in amplifier (EG & G Princeton Applied Research, Model 124A). Absorption frequencies were measured at room temperature using a beat frequency technique where a frequency synthesizer (300.0–3000.0 MHz, Model BSVB13, Bonn Hungary Electronics) was used as a local oscillator. The sample pressure was maintained around 20–30 mTorr during the experiment. The method of frequency measurement was described in [5]. The Stark voltage was kept around 500 V/cm. The uncertainty in frequency measurement was estimated to be ±0.15 MHz.
3. Spectral Analysis
Since the rotational constants and the potential barrier V3 hindering the internal rotation are fairly well known from the previous studies [10, 11] the assignments of the spectra for the high-J transitions were completed without much difficulty. Initially, the A and E components of high-J transitions were predicted in the frequency range 50.0–75.0 GHz using the known values of the rotational constants and the potential barrier. The computer program KC3IAM assembled by Kasten [12] from a modified version [13] of Wood’s classic treatment of a single top by the internal axis method [14] was used for prediction. Approximate values of A-E splitting were obtained for many transitions in the above frequency range. Around 100 transitions due to high K−1, K+1 with A-E splitting ranging from 6.3 MHz to 178.4 MHz were observed and measured.
Since the rotational Hamiltonian for the A-species transitions was similar in form to a rigid-rotor Hamiltonian with modified rotational constants [10] known as effective rotational constants [19] the A-species transitions were analyzed using the semirigid rotor Watson’s A-reduction Hamiltonian (Ir-representation) [20]. Newly measured A-species transitions are listed in Table 1 along with the transitions reported earlier in [10]. In all, 104 transitions were used in the least-squares analysis. Table 2 represents the values of effective rotational and centrifugal distortion constants and the value of the inertia defect for the A-species transitions after the final cycle of the fit. The standard deviation of the overall fit comes out to be 0.18 MHz.
| Transition | Frequency | Obs.-Cal. | ||||||
|---|---|---|---|---|---|---|---|---|
| J ′ | K ′ −1 | K ′ +1 | ← | J | K−1 | K+1 | ||
| 9 | 7 | 3 | 8 | 7 | 2 | 22919.90a | −.36 | |
| 10 | 2 | 9 | 9 | 2 | 8 | 22802.20a | −.13 | |
| 10 | 4 | 7 | 9 | 4 | 6 | 25605.20a | −.34 | |
| 10 | 6 | 5 | 9 | 6 | 4 | 25692.90a | −.16 | |
| 10 | 6 | 4 | 9 | 6 | 3 | 25720.60a | .04 | |
| 10 | 7 | 3 | 9 | 7 | 2 | 25546.60a | −.44 | |
| 10 | 8 | 2 | 9 | 8 | 1 | 25446.90a | .02 | |
| 10 | 9 | 1 | 9 | 9 | 0 | 25380.00a | .01 | |
| 13 | 5 | 9 | 12 | 5 | 8 | 33567.45a | −.20 | |
| 13 | 6 | 8 | 12 | 6 | 7 | 33776.80a | .00 | |
| 13 | 6 | 7 | 12 | 6 | 6 | 34250.80a | −.11 | |
| 13 | 7 | 7 | 12 | 7 | 6 | 33579.65a | −.10 | |
| 13 | 7 | 6 | 12 | 7 | 5 | 33628.74a | .12 | |
| 13 | 9 | 5 | 12 | 9 | 4 | 33217.40a | .28 | |
| 14 | 4 | 11 | 13 | 4 | 10 | 34626.90a | −.20 | |
| 14 | 7 | 8 | 13 | 7 | 7 | 36305.60a | −.25 | |
| 14 | 7 | 7 | 13 | 7 | 6 | 36433.93a | .15 | |
| 14 | 8 | 7 | 13 | 8 | 6 | 36058.00a | .32 | |
| 14 | 8 | 6 | 13 | 8 | 5 | 36067.50a | .15 | |
| 15 | 2 | 13 | 14 | 2 | 12 | 34764.70a | .09 | |
| 15 | 3 | 12 | 14 | 3 | 11 | 36977.20a | −.14 | |
| 15 | 4 | 12 | 14 | 4 | 11 | 36690.20a | .14 | |
| 15 | 6 | 10 | 14 | 6 | 9 | 39049.10a | −.06 | |
| 15 | 7 | 9 | 14 | 7 | 8 | 39041.60a | .24 | |
| 15 | 7 | 8 | 14 | 7 | 7 | 39339.60a | −.27 | |
| 15 | 8 | 8 | 14 | 8 | 7 | 38774.90a | .26 | |
| 15 | 8 | 7 | 14 | 8 | 6 | 38803.40a | .27 | |
| 16 | 4 | 13 | 15 | 4 | 12 | 38713.60a | .35 | |
| 18 | 0 | 18 | 17 | 0 | 17 | 36750.20a | .07 | |
| 20 | 7 | 13 | 19 | 7 | 12 | 55324.10 | .17 | |
| 21 | 7 | 14 | 20 | 7 | 13 | 58107.00 | −.08 | |
| 21 | 8 | 14 | 20 | 8 | 13 | 55125.30 | .05 | |
| 21 | 9 | 12 | 20 | 9 | 11 | 55578.20 | .30 | |
| 21 | 9 | 13 | 20 | 9 | 12 | 55076.80 | .24 | |
| 22 | 6 | 16 | 21 | 6 | 15 | 57746.00 | −.30 | |
| 22 | 7 | 15 | 21 | 7 | 14 | 60513.00 | .01 | |
| 22 | 8 | 14 | 21 | 8 | 13 | 60609.60 | −.16 | |
| 22 | 9 | 13 | 21 | 9 | 12 | 58791.90 | −.11 | |
| 22 | 12 | 10 | 21 | 12 | 9 | 56794.00 | −.21 | |
| 22 | 13 | 9 | 21 | 13 | 8 | 56556.80 | −.31 | |
| 22 | 14 | 8 | 21 | 14 | 7 | 56374.80 | −.01 | |
| 22 | 15 | 7 | 21 | 15 | 6 | 56230.60 | .20 | |
| 22 | 16 | 6 | 21 | 16 | 5 | 56113.80 | .28 | |
| 22 | 17 | 5 | 21 | 17 | 4 | 56017.10 | −.20 | |
| 22 | 18 | 4 | 21 | 18 | 3 | 55937.00 | .03 | |
| 22 | 19 | 3 | 21 | 19 | 2 | 55868.80 | −.28 | |
| 22 | 20 | 2 | 21 | 20 | 1 | 55811.10 | −.01 | |
| 23 | 21 | 2 | 22 | 21 | 1 | 58342.10 | .17 | |
| 23 | 20 | 3 | 22 | 20 | 2 | 58399.20 | .19 | |
| 23 | 19 | 4 | 22 | 19 | 3 | 58465.50 | .21 | |
| 23 | 18 | 5 | 22 | 18 | 4 | 58543.00 | .02 | |
| 23 | 17 | 6 | 22 | 17 | 5 | 58634.90 | −.13 | |
| 23 | 16 | 7 | 22 | 16 | 6 | 58745.40 | −.04 | |
| 23 | 15 | 8 | 22 | 15 | 7 | 58880.00 | .14 | |
| 23 | 14 | 9 | 22 | 14 | 8 | 59046.40 | −.06 | |
| 23 | 13 | 10 | 22 | 13 | 9 | 59257.70 | −.10 | |
| 23 | 12 | 11 | 22 | 12 | 10 | 59535.40 | −.14 | |
| 23 | 11 | 12 | 22 | 11 | 11 | 59931.00 | .07 | |
| 23 | 10 | 13 | 22 | 10 | 12 | 60633.20 | −.13 | |
| 23 | 9 | 14 | 22 | 9 | 13 | 62173.00 | .17 | |
| 23 | 6 | 17 | 22 | 6 | 16 | 59400.50 | .22 | |
| 24 | 23 | 1 | 23 | 23 | 0 | 60823.00 | −.11 | |
| 24 | 22 | 2 | 23 | 22 | 1 | 60872.60 | −.05 | |
| 24 | 21 | 3 | 23 | 21 | 2 | 60929.10 | .14 | |
| 24 | 20 | 4 | 23 | 20 | 3 | 60993.80 | −.03 | |
| 24 | 19 | 5 | 23 | 19 | 4 | 61068.90 | -.33 | |
| 24 | 18 | 6 | 23 | 18 | 5 | 61157.60 | −.09 | |
| 24 | 17 | 7 | 23 | 17 | 6 | 61262.60 | −.05 | |
| 24 | 16 | 8 | 23 | 16 | 7 | 61388.80 | .01 | |
| 24 | 15 | 9 | 23 | 15 | 8 | 61542.60 | −.12 | |
| 24 | 14 | 10 | 23 | 14 | 9 | 61734.20 | −.01 | |
| 24 | 13 | 11 | 23 | 13 | 10 | 61978.30 | −.35 | |
| 24 | 12 | 12 | 23 | 12 | 11 | 62305.00 | .19 | |
| 24 | 12 | 13 | 23 | 12 | 12 | 62297.00 | .07 | |
| 24 | 11 | 13 | 23 | 11 | 12 | 62793.30 | −.22 | |
| 24 | 11 | 14 | 23 | 11 | 13 | 62709.60 | .19 | |
| 24 | 6 | 18 | 23 | 6 | 17 | 61127.50 | .12 | |
| 25 | 6 | 19 | 24 | 6 | 18 | 62935.70 | .06 | |
| 25 | 8 | 17 | 24 | 8 | 16 | 68834.00 | −.07 | |
| 25 | 9 | 16 | 24 | 9 | 15 | 69015.60 | .09 | |
| 25 | 9 | 17 | 24 | 9 | 16 | 65732.10 | .28 | |
| 25 | 10 | 15 | 24 | 10 | 14 | 67048.00 | .09 | |
| 25 | 24 | 1 | 24 | 24 | 0 | 63354.70 | .38 | |
| 25 | 23 | 2 | 24 | 23 | 1 | 63403.20 | −.07 | |
| 25 | 22 | 3 | 24 | 22 | 2 | 63458.70 | −.18 | |
| 26 | 8 | 18 | 25 | 8 | 17 | 70796.70 | .10 | |
| 26 | 10 | 16 | 25 | 10 | 15 | 70507.00 | .18 | |
| 26 | 12 | 14 | 25 | 12 | 13 | 67953.00 | −.16 | |
| 26 | 14 | 12 | 25 | 14 | 11 | 67163.60 | .06 | |
| 26 | 22 | 4 | 25 | 22 | 3 | 66051.30 | −.01 | |
| 27 | 9 | 19 | 26 | 9 | 18 | 70443.10 | .05 | |
| 27 | 11 | 17 | 26 | 11 | 16 | 71220.20 | −.27 | |
| 27 | 12 | 15 | 26 | 12 | 14 | 70856.10 | .06 | |
| 27 | 13 | 14 | 26 | 13 | 13 | 70288.20 | −.21 | |
| 28 | 22 | 6 | 27 | 22 | 5 | 71256.00 | .13 | |
| 28 | 24 | 4 | 27 | 24 | 3 | 71108.90 | −.10 | |
| 28 | 26 | 2 | 27 | 26 | 1 | 70994.40 | .11 | |
| 29 | 22 | 7 | 28 | 22 | 6 | 73868.50 | −.10 | |
| 29 | 24 | 5 | 28 | 24 | 4 | 73705.30 | .03 | |
| 29 | 25 | 4 | 28 | 25 | 3 | 73637.80 | −.03 | |
| 29 | 26 | 3 | 28 | 26 | 2 | 73577.80 | −.09 | |
| 29 | 27 | 2 | 28 | 27 | 1 | 73524.40 | .09 | |
| 29 | 28 | 1 | 28 | 28 | 0 | 73476.20 | .03 | |
| 30 | 7 | 24 | 29 | 7 | 23 | 72553.20 | −.02 | |
- a[10].
| Constants | This work |
|---|---|
| A/MHz | 2892.79 (6) |
| B/MHz | 1500.409 (7) |
| C/MHz | 993.507 (8) |
| ∆J/kHz | −0.032 (7) |
| ∆JK/kHz | 0.830 (38) |
| ∆K/kHz | −1.31 (41) |
| δj/kHz | 0.045 (4) |
| δk/kHz | −0.58 (8) |
| ∆ = (Ic-Ib–Ia)/ u Å2 | −2.85 |
The assigned E-species lines appear close to their predicted values. Table 3 shows the observed and measured E-species lines and the splitting due to internal rotation of the CH3 top. The observed A-E splittings of Table 3 were analyzed using KC3IAM program. An iterative least-squares analysis was performed with 92 observed A-E splitting which includes 12 from [10]. Two separate fits were performed. In Fit 1, three independent parameters, namely, the top moment of inertia Iα, the potential barrier V3 and θa, the angle between the internal rotation axis and the principal axis a were allowed to vary. In Fit 2, two independent parameters, namely, V3 and θa were allowed to vary and Iα was fixed to 3.2 u Å2 [4]. The “true” rotational and centrifugal distortion constants reported in [11] were used as fixed parameters in these fits. The results of the internal rotation analysis are presented in Table 4. A comparison of Fit 1 and Fit 2 reveals that parameters in Fit 2 are more accurately determined than that of Fit 1.
| J ′ | K ′ −1 | K ′ +1 | ← | J | K−1 | K+1 | Frequency | ν A-νE | Obs.-Calc. |
|---|---|---|---|---|---|---|---|---|---|
| 13 | 7 | 6 | 12 | 7 | 5 | 33584.23b | 44.51 | −0.15 | |
| 13 | 9 | 5 | 12 | 9 | 4 | 33209.55b | 7.85 | 0.44 | |
| 14 | 4 | 11 | 13 | 4 | 10 | 34619.10b | 7.80 | 0.09 | |
| 14 | 7 | 8 | 13 | 7 | 7 | 36358.30b | −52.7 | −0.35 | |
| 14 | 7 | 7 | 13 | 7 | 6 | 36352.38b | 81.55 | 0.42 | |
| 14 | 8 | 6 | 13 | 8 | 5 | 36042.13b | 25.37 | −0.04 | |
| 15 | 3 | 13 | 14 | 3 | 12 | 34735.40b | 6.30 | 0.47 | |
| 15 | 6 | 10 | 14 | 6 | 9 | 39083.80b | −34.70 | −0.43 | |
| 15 | 7 | 8 | 14 | 7 | 7 | 39207.80b | 131.80 | −0.16 | |
| 15 | 8 | 8 | 14 | 8 | 7 | 38782.25b | −7.35 | 0.46 | |
| 15 | 8 | 7 | 14 | 8 | 6 | 38765.50b | 37.90 | 0.31 | |
| 16 | 4 | 13 | 15 | 4 | 12 | 38705.90b | 7.70 | −0.42 | |
| 21 | 7 | 14 | 20 | 7 | 13 | 58077.80 | 29.20 | 0.48 | |
| 21 | 8 | 13 | 20 | 8 | 12 | 57193.00 | 74.00 | 0.47 | |
| 21 | 8 | 14 | 20 | 8 | 13 | 55149.10 | −23.80 | −0.27 | |
| 21 | 9 | 12 | 20 | 9 | 11 | 55399.80 | 178.40 | 0.47 | |
| 22 | 9 | 13 | 21 | 9 | 12 | 58624.00 | 167.60 | −0.25 | |
| 22 | 6 | 16 | 21 | 6 | 15 | 57732.80 | 13.00 | −0.46 | |
| 22 | 7 | 15 | 21 | 7 | 14 | 60489.60 | 23.40 | −0.26 | |
| 22 | 8 | 14 | 21 | 8 | 13 | 60558.40 | 51.20 | 0.24 | |
| 22 | 12 | 10 | 21 | 12 | 9 | 56763.20 | 30.80 | −0.26 | |
| 22 | 13 | 9 | 21 | 13 | 8 | 56528.20 | 28.50 | −0.06 | |
| 22 | 14 | 8 | 21 | 14 | 7 | 56347.80 | 27.00 | −0.14 | |
| 22 | 15 | 7 | 21 | 15 | 6 | 56204.20 | 26.40 | 0.25 | |
| 22 | 16 | 6 | 21 | 16 | 5 | 56088.20 | 25.80 | 0.40 | |
| 22 | 17 | 5 | 21 | 17 | 4 | 55992.40 | 24.40 | −0.41 | |
| 22 | 18 | 4 | 21 | 18 | 3 | 55912.30 | 24.70 | 0.33 | |
| 22 | 19 | 3 | 21 | 19 | 2 | 55845.10 | 23.70 | −0.30 | |
| 23 | 6 | 17 | 22 | 6 | 16 | 59387.40 | 13.10 | −0.15 | |
| 23 | 9 | 14 | 22 | 9 | 13 | 62056.80 | 116.20 | −0.05 | |
| 23 | 10 | 13 | 22 | 10 | 12 | 60476.00 | 157.20 | −0.23 | |
| 23 | 11 | 12 | 22 | 11 | 11 | 59876.40 | 54.60 | 0.11 | |
| 23 | 12 | 11 | 22 | 12 | 10 | 59501.20 | 34.20 | −0.38 | |
| 23 | 13 | 10 | 22 | 13 | 9 | 59226.90 | 30.80 | 0.02 | |
| 23 | 14 | 9 | 22 | 14 | 8 | 59017.00 | 29.40 | 0.36 | |
| 23 | 15 | 8 | 22 | 15 | 7 | 58851.80 | 28.20 | 0.34 | |
| 23 | 16 | 7 | 22 | 16 | 6 | 58718.30 | 27.10 | 0.12 | |
| 23 | 17 | 6 | 22 | 17 | 5 | 58608.40 | 26.30 | 0.01 | |
| 23 | 18 | 5 | 22 | 18 | 4 | 58517.10 | 25.90 | 0.12 | |
| 23 | 19 | 4 | 22 | 19 | 3 | 58439.90 | 25.90 | 0.54 | |
| 23 | 20 | 3 | 22 | 20 | 2 | 58374.00 | 25.40 | 0.39 | |
| 23 | 21 | 2 | 22 | 21 | 1 | 58317.10 | 25.00 | 0.28 | |
| 24 | 6 | 18 | 23 | 6 | 17 | 61113.90 | 13.60 | 0.02 | |
| 24 | 11 | 13 | 23 | 11 | 12 | 62712.80 | 80.20 | −0.27 | |
| 24 | 11 | 14 | 23 | 11 | 13 | 62740.00 | −30.00 | −0.11 | |
| 24 | 12 | 12 | 23 | 12 | 11 | 62264.90 | 40.10 | 0.20 | |
| 24 | 13 | 11 | 23 | 13 | 10 | 61945.10 | 33.20 | −0.07 | |
| 24 | 13 | 12 | 23 | 13 | 11 | 61965.60 | 12.80 | 0.17 | |
| 24 | 14 | 10 | 23 | 14 | 9 | 61702.80 | 31.40 | 0.35 | |
| 24 | 15 | 9 | 23 | 15 | 8 | 61513.20 | 29.40 | −0.24 | |
| 24 | 15 | 10 | 23 | 15 | 9 | 61529.00 | 13.60 | 0.09 | |
| 24 | 16 | 8 | 23 | 16 | 7 | 61360.40 | 28.40 | −0.22 | |
| 24 | 16 | 9 | 23 | 16 | 8 | 61375.30 | 13.50 | 0.03 | |
| 24 | 17 | 7 | 23 | 17 | 6 | 61234.60 | 28.00 | 0.16 | |
| 24 | 17 | 8 | 23 | 17 | 7 | 61249.30 | 13.30 | 0.01 | |
| 24 | 18 | 6 | 23 | 18 | 5 | 61130.40 | 27.20 | −0.03 | |
| 24 | 18 | 7 | 23 | 18 | 6 | 61145.00 | 12.60 | −0.43 | |
| 24 | 19 | 5 | 23 | 19 | 4 | 61042.30 | 26.60 | −0.14 | |
| 24 | 19 | 6 | 23 | 19 | 5 | 61056.70 | 12.20 | −0.52 | |
| 24 | 20 | 4 | 23 | 20 | 3 | 60967.30 | 26.50 | 0.16 | |
| 24 | 21 | 3 | 23 | 21 | 2 | 60903.00 | 26.10 | 0.09 | |
| 24 | 22 | 2 | 23 | 22 | 1 | 60847.00 | 25.60 | −0.11 | |
| 24 | 23 | 1 | 23 | 23 | 0 | 60798.10 | 25.30 | −0.16 | |
| 25 | 24 | 1 | 24 | 24 | 0 | 63328.00 | 26.70 | 0.25 | |
| 25 | 24 | 2 | 24 | 24 | 1 | 63343.80 | 10.90 | −0.19 | |
| 25 | 23 | 2 | 24 | 23 | 1 | 63376.50 | 26.70 | −0.01 | |
| 25 | 23 | 3 | 24 | 23 | 2 | 63392.10 | 11.10 | −0.47 | |
| 25 | 22 | 3 | 24 | 22 | 2 | 63431.40 | 27.30 | 0.31 | |
| 25 | 22 | 4 | 24 | 22 | 3 | 63447.10 | 11.60 | −0.43 | |
| 25 | 6 | 19 | 24 | 6 | 18 | 62921.80 | 14.10 | 0.12 | |
| 25 | 8 | 17 | 24 | 8 | 16 | 68807.80 | 26.20 | 0.26 | |
| 25 | 9 | 17 | 24 | 9 | 16 | 65728.90 | 3.20 | −0.11 | |
| 25 | 10 | 15 | 24 | 10 | 14 | 66877.50 | 170.50 | −0.29 | |
| 25 | 22 | 4 | 25 | 22 | 3 | 66022.80 | 28.50 | 0.21 | |
| 26 | 14 | 12 | 25 | 14 | 11 | 67128.20 | 35.40 | −0.16 | |
| 26 | 12 | 14 | 25 | 12 | 13 | 67887.10 | 65.90 | −0.22 | |
| 26 | 10 | 16 | 25 | 10 | 15 | 70390.50 | 116.50 | −0.22 | |
| 26 | 8 | 18 | 25 | 8 | 17 | 70775.70 | 21.00 | −0.09 | |
| 27 | 12 | 15 | 26 | 12 | 14 | 70759.10 | 97.00 | −0.31 | |
| 27 | 9 | 19 | 26 | 9 | 18 | 70426.50 | 17.00 | −0.10 | |
| 27 | 13 | 14 | 26 | 13 | 13 | 70241.90 | 46.30 | −0.50 | |
| 27 | 11 | 17 | 26 | 11 | 16 | 71365.20 | 145.00 | 0.09 | |
| 28 | 22 | 6 | 27 | 22 | 5 | 71224.90 | 31.10 | 0.12 | |
| 28 | 24 | 4 | 27 | 24 | 3 | 71078.90 | 30.00 | 0.21 | |
| 28 | 26 | 2 | 27 | 26 | 1 | 70964.60 | 30.00 | 0.40 | |
| 29 | 22 | 7 | 28 | 22 | 6 | 73836.10 | 32.40 | 0.04 | |
| 29 | 24 | 5 | 28 | 24 | 4 | 73673.60 | 31.70 | 0.19 | |
| 29 | 25 | 4 | 28 | 25 | 3 | 73606.70 | 31.10 | −0.05 | |
| 29 | 26 | 3 | 28 | 26 | 2 | 73547.00 | 30.80 | −0.02 | |
| 29 | 27 | 2 | 28 | 27 | 1 | 73493.90 | 30.50 | −0.02 | |
| 29 | 28 | 1 | 28 | 28 | 0 | 73446.10 | 30.10 | −0.13 | |
| 30 | 7 | 24 | 29 | 7 | 23 | 72544.30 | 8.90 | −0.25 |
- b[10].
| Constants | Experimental values | DFT values | |
|---|---|---|---|
| A/MHz | 2891.6469 (5)c | 2884.36 | |
| B/MHz | 1499.8809 (1)c | 1506.90 | |
| C/MHz | 993.5217 (6)c | 995.84 | |
| ∆J/kHz | 0.039 (1)c | 0.0403 | |
| ∆JK/kHz | 0.396 (5)c | 0.327 | |
| ∆K/kHz | 0.38 (5)c | 0.601 | |
| δj/kHz | 0.0116 (6)c | 0.0131 | |
| δk/kHz | 0.236 (8)c | 0.206 | |
| Fit 1 | Fit 2 | DFT values | |
| Iα/u Å2 | 3.23 ± 0.01 | 3.2 (fixed) | 3.25 |
| θa/degree | 53.33 ± 0.09 | 53.50 ± 0.03 | 55.45 |
| θb/degree | 36.67 ± 0.09 | 36.50 ± 0.03 | 34.55 |
| V3/cal/mol | 533.47 ± 2.8 | 537.71 ± 0.10 | 608.41 |
- c[11].
4. DFT Calculation
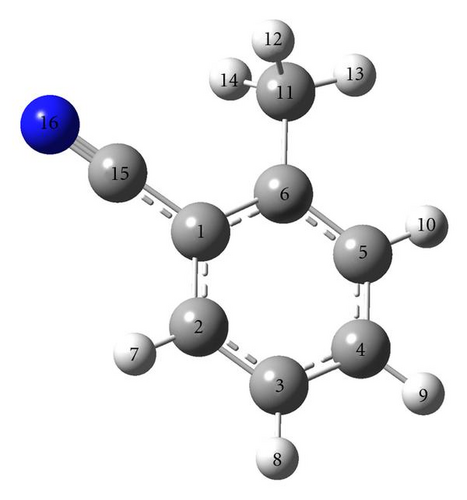
Quantum mechanical calculations were performed via the density functional theory (DFT) using Gaussian 03 package [21] implemented on Intel Core 2 machine. The calculations were performed to determine the structural parameters, rotational constants, centrifugal distortion constants and internal rotation parameters Iα, θa, θb, and barrier to internal rotation (V3) of the methyl top of o-tolunitrile. The moment of inertia of the methyl group Iα is obtained by assuming C6–C11 bond as fixed axis of rotation and θa, θb were obtained from structural data. The geometry optimization is carried out using Becke three parameter hybrid functional and Lee, Yang, Parr nonlocal correlation functional (B3LYP) with relatively large basis set 6-311G (3d, p). The torsional potential curve of the methyl top is obtained by varying the dihedral angle of one methyl hydrogen from 0° to 360° relative to the molecular framework in steps of 10° on the optimized geometry. The molecular drawing is done by using GaussView 3.0 software package [22]. The number and labeling of o-tolunitrile molecule is shown in Figure 1.
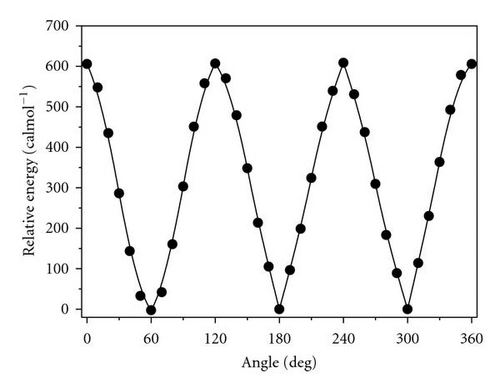
All torsional potential values were calculated with respect to the lowest energy configuration of o-tolunitrile. The calculated potential function is shown in Figure 2. The potential barrier V3 calculated by DFT method is found to be 608.41 cal/mol which is comparable with the experimental value of 537.71 cal/mol. The calculated values of rotational constants, centrifugal distortion constants, and internal rotation parameters obtained from DFT theoretical calculations have been compared with the corresponding experimental values and are shown in Table 4. The agreement is found to be highly satisfactory.
In Table 5 the potential barrier V3 values of o-tolunitrile have been compared with other related molecules. Structural parameters of o-tolunitrile have been computed and are shown in Table 6.
| Sample name | Chemical formula | V3 (Cal/mol) | Ref. |
|---|---|---|---|
| o-Fluorotoluene | o-C6H4CH3F | 649.30 | [2] |
| o-35Chlorotoluene | o-C6H4CCl | 1328.524/1343.262d | [15, 16] |
| o-37Chlorotoluene | o-C6H4CCl | 1327.857/1339.976d | [15, 16] |
| 2,4-Difluorotoluene | C6H3CH3F2 | 583.002 ± 0.668 | [5] |
| o-Xylene | C6H4CH3CH3 | 1482 ± 9 | [17] |
| syn-o-Cresol | syn-o-C6H4CH3OH | 1883.809d | [18] |
| anti-o-Cresol | anti-o-C6H4CH3OH | 1053.714d | [18] |
| o-Tolunitrile | o-C6H4CH3CN | 533.53 ± 0.58 | [10] |
| 534.614e | [11] | ||
| 537.71 ± 0.10 | This work | ||
| o-Toluidine | o-C6H4CH3NH2 | 2002.3e | [6] |
- dConverted from kJ/mol to Cal/mol, econverted from cm−1 to Cal/mol.
| Distances (pm) | Angles (°) | Dihedral angles (°) | |||
|---|---|---|---|---|---|
| C1–C2 | 140.04 | C1–C2–C3 | 120.0508 | ||
| C2–C3 | 138.70 | C2–C3–C4 | 119.5363 | ||
| C3–C4 | 139.12 | C3–C4–C5 | 120.2915 | ||
| C4–C5 | 139.15 | C4–C5–C6 | 121.4869 | ||
| C5–C6 | 139.39 | C5–C6–C1 | 117.5412 | ||
| C1–C6 | 140.97 | C1–C6–C11 | 121.0341 | ||
| C2–H7 | 108.29 | C3–C2–H7 | 120.7200 | ||
| C3–H8 | 108.32 | C4–C3–H8 | 120.4898 | ||
| C4–H9 | 108.39 | C5–C4–H9 | 119.6849 | ||
| C1–C15 | 143.16 | C2–C1–H15 | 119.3137 | ||
| C15–N16 | 116.77 | C6–C1–C15 | 119.8284 | ||
| C6–C11 | 150.53 | C5–C6–C11 | 121.3573 | ||
| C5-H10 | 108.44 | C6–C5–H10 | 118.8873 | ||
| C11-H12 | 109.33 | C6–C11–H12 | 111.1996 | C1–C6-C11–H12 | 59.4310 |
| C11-H13 | 109.04 | C6-C11-H13 | 110.9089 | C1–C6-C11–H13 | −179.9726 |
| C11-H14 | 109.33 | C6-C11-H14 | 111.2012 | C1–C6-C11–H14 | −59.3797 |
5. Conclusions
The millimeterwave rotational spectra of o-tolunitrile have been measured in the frequency range 50.0–75.0 GHz in the ground torsional state. Many high-J (Jmax= 30) rotational transitions with large A-E splitting have been assigned. The analysis of these splitting allows us to determine the internal rotation parameters more accurately. A comparison of the V3 values of different toluene derivatives (Table 5) indicates that a heavier substituent such as a chlorine atom or methyl groups on the toluene ring leads to an enhancement of the torsional barrier values from the corresponding V3 values obtained in cases where a lighter substituent such as a fluorine atom or a cyanogen group is attached to the ring. To support the experimental results, DFT calculations were carried out with DFT/B3LYP/6-311G (3d, p) basis set. The parameters obtained by DFT calculations were found to be in good agreement with those observed experimentally.
Acknowledgments
A. I. Jaman would like to thank Mr. A. K. Bhattacharya for his technical assistance during the course of this paper. P. R. Bangal gratefully acknowledges support from the DST, Government of India, Grant no. SR/FTP/CS-93/2005.




