This paper presents a global optimization method for solving general nonlinear programming problems subjected to box constraints. Regardless of convexity or nonconvexity, by introducing a differential flow on the dual feasible space, a set of complete solutions to the original problem is obtained, and criteria for global optimality and existence of solutions are given. Our theorems improve and generalize recent known results in the canonical duality theory. Applications to a class of constrained optimal control problems are discussed. Particularly, an analytical form of the optimal control is expressed. Some examples are included to illustrate this new approach.

1. Introduction

In this paper, we consider the following general box constrained nonlinear programming problem (the primal problem (𝒫) in short):

()

where 𝒳_a = {x ∈ ℛⁿ∣ℓ^l ≤ x ≤ ℓ^u} is a feasible space, ℓ^l, ℓ^u ∈ ℛⁿ are two given vectors, and P(x) is twice continuously differentiable in ℛⁿ. Here, we discuss the primal problem (𝒫) involving nonconvexity or convexity in the objective function.

Problem (1.1) appears in many applications, such as engineering design, phase transitions, chaotic dynamics, information theory, and network communication [1, 2]. Particularly, if ℓ^l = {0} and ℓ^u = {1}, the problem leads to one of the fundamental problems in combinatorial optimization, namely, the integer programming problem [3]. By the fact that the feasible space 𝒳_a is a closed convex subset of ℛⁿ, the primal problem has at least one global minimizer. When (𝒫) is a convex programming problem, a global minimizer can be obtained by many well-developed nonlinear optimization methods based on the Karush-Kuhn-Tucker (or simply KKT ) optimality theory [4]. However, for (𝒫) with nonconvexity in the objective function, traditional KKT theory and direct methods can only be used for solving (𝒫) to local optimality. So, our interest will be mainly in the case of P(x) being nonconvex on 𝒳_a in this paper. For special cases of minimizing a nonconvex quadratic function subject to box constraints, much effort and progress have been made on locating the global optimal solution based on the canonical duality theory by Gao (see [5–7] for details). As indicated in [8], the key step of the canonical duality theory is to introduce a canonical dual function, but commonly used methods are not guaranteed to construct it since the general form of the objective function given in (1.1). Thus, there has been comparatively little work in global optimality for general cases.

Inspired and motivated by these facts, a differential flow for constructing the canonical dual function is introduced and a new approach to solve the general (especially nonconvex) nonlinear programming problem (𝒫) is investigated in this paper. By means of the canonical dual problem, some conditions in global optimality are deduced, and global and local extrema of the primal problem can be identified. An application to the linear-quadratic optimal control problem with constraints is discussed. These results presented in this paper can be viewed as an extension and an improvement in the canonical duality theory [8–10].

The paper is organized as follows. In Section 2, a differential flow is introduced to present a general form of the canonical dual problem to (𝒫). The relation of this transformation with the classical Lagrangian method is discussed. In Section 3, we present a set of complete solutions to (𝒫) by the way presented in Section 2. The existence of the canonical dual solutions is also given. We give an analytic solution to the box-constrained optimal control problem via canonical dual variables in Section 4. Meanwhile, some examples are used to illustrate our theory.

2. A Differential Flow and Canonical Dual Problem

In the beginning of this paper, we have mentioned that our primal goal is to find the global minimizers to a general (mainly nonconvex) box-constrained optimization problem (𝒫). Due to the assumed nonconvexity of the objective function, the classical Lagrangian L(x, σ) is no longer a saddle function, and the Fenchel-Young inequality leads to only a weak duality relation: min P ≥ max P^*. The nonzero value θ = min P(x) − max P^*(σ) is called the duality gap, where possibly, θ = ∞. This duality gap shows that the well-developed Fenchel-Moreau-Rockafellar duality theory can be used mainly for solving convex problems. Also, due to the nonconvexity of the objective function, the problem may have multiple local solutions. The identification of a global minimizer has been a fundamentally challenging task in global optimization. In order to eliminate this duality gap inherent in the classical Lagrange duality theory, a so-called canonical duality theory has been developed [2, 9]. The main idea of this new theory is to introduce a canonical dual transformation which may convert some nonconvex and/or nonsmooth primal problems into smooth canonical dual problems without generating any duality gap and deduce some global solutions. The key step in the canonical dual transformation is to choose the (nonlinear) geometrical operator Λ(x). Different forms of Λ(x) may lead to different (but equivalent) canonical dual functions and canonical dual problems. So far, in most literatures related, the canonical dual transformation is discussed and the canonical dual function is formulated in quadratic minimization problems (i.e., the objective function is the quadratic form). However, for the general form of the objective function given in (1.1), in general, it lacks effective strategies to get the canonical dual function (or the canonical dual problem) by commonly used methods. The novelty of this paper is to introduce the differential flow created by differential equation (2.6) to construct the canonical dual function for the problem (𝒫). Lemma 2.5 guarantees the existence of the differential flow; Theorem 2.3 shows that there is no duality gap between the primal problem (𝒫) and its canonical dual problem (P^d) given in (2.7) via the differential flow; Meanwhile, Theorems 3.1–3.4 use the differential flow to present a global minimizer. In addition, the idea to introduce the set 𝒮 of shift parameters is closely following the works by Floudas et al. [11, 12]. In [12], they developed a global optimization method, αBB, for general twice-differentiable constrained optimizations proposing to utilize some α parameter to generate valid convex under estimators for nonconvex terms of generic structure.

The main idea of constructing the differential flow and the canonical dual problem is as follows. For simplicity without generality, we assume that , namely, , where ℓ_i ≠ 0 for all i.

Let 𝒮 denote the dual feasible space

()

where

, and Diag(ρ) ∈ ℛ^n×n is a diagonal matrix with ρ_i, i = 1,2, …, n, as its diagonal entries.

Lemma 2.1. The dual feasible space 𝒮 is an open convex subset of . If , then ρ ∈ 𝒮 for any .

Proof. Notice that P(x) is twice continuously differentiable in ℛⁿ. For any x ∈ 𝒳_a, the Hessian matrix ∇²P(x) is a symmetrical matrix. We know that for any given Q = Q^T ∈ ℛ^n×n, is a convex set. By the fact that the intersection of any collection of convex sets is convex, the dual feasible space 𝒮 is an open convex subset of . In addition, it follows from the definition of 𝒮 that ρ ∈ 𝒮 for any . This completes the proof.

Suppose that ρ^* ∈ 𝒮 and a nonzero vector x^* ∈ 𝒳_a satisfy

()

A differential flow x(ρ) is introduced over a relative small neighborhood of ρ^* such that

()

which is equivalent to

()

where ∇x(ρ) is the Jacobian of x and is a matrix whose ijth entry is equal to the partial derivative ∂x_i/∂ρ_j. Here, we hope to preserve invertibility of the matrix ∇²P(x(ρ)) + Diag(ρ) on the choice of the neighborhood of ρ^*.

Let

()

Then, a differential flow x(ρ) can be defined by the following differential system:

()

where H_ij(ρ) is the ijth entry of H(ρ, x(ρ)). Based on the Extension theory [13, 14], the solution x(ρ) of the differential system (2.6) can be extended to a space in 𝒮. The canonical dual function is defined as

()

Thus, the canonical dual problem for our primal problem (𝒫) can be proposed as follows

()

In the following, we show that (P^d) is canonically (i.e., with zero duality gap) dual to (𝒫).

Lemma 2.2. Let x(ρ) be a given flow defined by (2.6), and P^d(ρ) be the corresponding canonical dual function defined by (2.7). For any ρ ∈ 𝒮, we have

()

Proof. Since P^d(ρ) is differentiable, for any ρ ∈ 𝒮,

()

It follows from the process (2.2)–(2.6) that

()

From (2.6), we have ∂x_i(ρ)/∂ρ_j = H_ij(ρ)x_j(ρ). By (2.11), then

()

By the definition of H(ρ, x(ρ)), this concludes the proof of Lemma 2.2.

By Lemma 2.2, the canonical dual function P^d(ρ) is concave on 𝒮. For a critical point,

must be a global maximizer of (P^d), and it can be solved by many well-developed nonlinear programming methods. If

and

, we have

, and for any

, by negative definiteness of H(x(ρ), ρ),

()

Thus for any

, x(ρ) will stay in 𝒳_a and

Theorem 2.3. The canonical dual problem (P^d) is perfectly dual to the primal problem (𝒫) in the sense that if is a KKT point of P^d(ρ), then the vector is a KKT point of (𝒫) and

()

Proof. By introducing the Lagrange multiplier vector λ ∈ ℛⁿ to relax the inequality constraint ρ ≥ 0 in 𝒮, the Lagrangian function associated with (P^d) becomes L(ρ, λ) = P^d(ρ) − λ^Tρ.Then the KKT conditions of (P^d) become

()

Notice that

. It follows from conditions (2.15) that

satisfies the complementary conditions of (𝒫). By the definition of the flow x(ρ), the equation

holds. This proved that if

is a KKT point of P^d(ρ), then the vector

defined by (2.6) is a KKT point of the primal problem (𝒫).

In addition, we have

()

This completes the proof.

Remark 2.4. Theorem 2.3 shows that by using the canonical dual function (2.7), there is no duality gap between the primal problem (𝒫) and its canonical dual (P^d), that is, θ = 0. It eliminates this duality gap inherent in the classical Lagrange duality theory and provides necessary conditions for searching global solutions. Actually, we replace 𝒮 in (P^d) with the space 𝒮_#, 𝒮_# : = {ρ ≥ 0∣det [∇²P(x) + Diag(ρ)] ≠ 0, for all x ∈ 𝒳_a} in the proof of Theorem 2.3. Moreover, the inequality of det [∇²P(x) + Diag(ρ)] ≠ 0, for all x ∈ 𝒳_a in 𝒮_# is essentially not a constraint as indicated in [5].

Due to introduceing a differential flow x(ρ), the constrained nonconvex problem can be converted to the canonical (perfect) dual problem, which can be solved by deterministic methods. In view of the process (2.2)–(2.6), the flow x(ρ) is based on the KKT (2.2). In other words, we can solve equation (2.2) backwards from ρ^* to get the backward flow x(ρ), ρ ∈ 𝒮∩{0 ≤ ρ ≤ ρ^*}. Then, it is of interest to know whether there exists a pair (x^*, ρ^*) satisfying (2.2).

Lemma 2.5. Suppose that ∇P(0) ≠ 0. For the primal problem (𝒫), there exist a point ρ^* ∈ 𝒮 and a nonzero vector x^* ∈ 𝒳_a such that ∇P(x^*) + Diag(ρ^*)x^* = 0.

Proof. Since 𝒳_a is bounded and P(x) is twice continuously differentiable in ℛⁿ, we can choose a large positive real M ∈ ℛ such that ∇²P(x) + Diag(Me) > 0, for all x ∈ 𝒳_a and (e ∈ ℛⁿ is an n−vector of all ones). Then, it is easy to verify that ∇P(x) + Diag(Me)x < 0 at the point x = −ℓ^1/2, and ∇P(x) + Diag(Me)x > 0 at the point x = ℓ^1/2.

Notice that the function ∇P(x) + Diag(Me)x is continuous and differentiable in ℛⁿ. It follows from differential and integral calculus that there is a nonzero stationary point x^* ∈ 𝒳_a such that ∇P(x^*) + Diag(Me)x^* = 0. Let ρ^* = Me ∈ 𝒮. Thus, there exist a point ρ^* ∈ 𝒮 and a nonzero vector x^* ∈ 𝒳_a satisfying (2.2). This completes the proof.

Remark 2.6. Actually, Lemma 2.5 gives us some information to search the desired parameter ρ^*. From Lemma 2.5, we only need to choose a large positive real M ∈ ℛ such that ∇²P(x) + Diag(Me) > 0, for all x ∈ 𝒳_a and . Since ∇P(0) ≠ 0, then it follows from (∥∇²P(x)∥/M) < 1 uniformly in 𝒳_a that there is a unique nonzero fixed point x^* ∈ 𝒳_a such that

()

which is equivalent to ∇P(x^*) + Diag(Me)x^* = 0 by Brown fixed-point theorem. In [11, 12], some good algorithms are given to estimate the bounds of ∥∇²P(x)∥. If there is a positive real number K such that ∥∇²P(x)∥ ≤ K, for all x ∈ 𝒳_a, then a properly large parameter M can be obtained by the inequalities

()

uniformly on 𝒳_a for us to use Brown fixed-point theorem. We should choose

()

Finally, let ρ^* = Me which is the desired parameter ρ^* for us. We will discuss to calculate the parameter ρ^* in detail by the use of the results in [15, 16] with the future works.

Remark 2.7. Moreover, for the proper parameter ρ^*, it is worth investigating how to get the solution x^* of (2.2) inside of 𝒳_a. For this issue, when P(x) is a polynomial, we may be referred to [17]. There are results in [17] on bounding the zeros of a polynomial. We may consider for a given bounds to determine the parameter by the use of the results in [17] on the relation between the zeros and the coefficients. We will discuss it with the future works as well. However, the KKT conditions are only necessary conditions for local minimizers to satisfy for the nonconvex case of (𝒫). To identify, a global minimizer among all KKT points remains a key task for us to address in the next section.

3. Complete Solutions to Global Optimization Problems

Theorem 3.1. Suppose that is a KKT point of the canonical dual function P^d(ρ) and defined by (2.6). If , then is a global maximizer of (P^d) on 𝒮, and is a global minimizer of (𝒫) on 𝒳_a and

()

Proof. If is a KKT point of (P^d) on 𝒮, by (2.15), stays in 𝒳_a, that is, for all i. By Lemma 2.1 and 2.2, it is easy to verify that x(ρ) ∈ 𝒳_a and for any .

For any given parameter ρ, (), we define the function f_ρ(x) as follows:

()

It is obvious that P(x) ≥ f_ρ(x) for all x ∈ 𝒳_a. Since f_ρ(x) is twice continuously differentiable in ℛⁿ, there exists a closed convex region ℰ containing 𝒳_a such that on ℰ,

()

This implies that x(ρ) is the unique global minimizer of f_ρ(x) over ℰ. By (2.7), we have

()

Thus, for any

()

On the other hand, by the fact that the canonical dual function P^d(ρ) is concave on 𝒮,

must be a global maximizer of (P^d) on 𝒮, and we have

()

and for all x ∈ 𝒳_a,

()

Thus, is a global minimizer of (𝒫) on 𝒳_a and

()

This completes the proof.

Remark 3.2. Theorem 3.1 shows that a vector is a global minimizer of the problem (𝒫) if is a critical solution of (P^d). However, for certain given P(x), the canonical dual function might have no critical point in 𝒮. For example, the canonical dual solutions could locate on the boundary of 𝒮. In this case, the primal problem (𝒫) may have multiple solutions.

In order to study the existence conditions of the canonical dual solutions, we let ∂𝒮 denote the boundary of 𝒮.

Theorem 3.3. Suppose that P(x) is a given twice continuously differentiable function, 𝒮 ≠ ∅ and ∂𝒮 ≠ ∅. If for any given ρ₀ ∈ ∂𝒮 and ρ ∈ 𝒮,

()

then the canonical dual problem (P^d) has a critical point

, and

is a global minimizer to (𝒫).

Proof. We first show that for any given ,

()

Notice that there exist a point ρ^* ∈ 𝒮 and a nonzero vector x(ρ^*) ∈ 𝒳_a. For any given

, the inequality

always holds as α₀ > 0 becomes large enough. Then for any α ≥ α₀, it follows from Lemma 2.1 and 2.2 that

and

stays in 𝒳_a, that is,

. It means that there exists a large positive real L such that

for α ≥ α₀ since P(x) is twice continuously differentiable in ℛⁿ.

By Lemma 2.2, we have

()

where

. For any α ≥ α₀, by the definition of 𝒮, it is easy to see that

, namely,

monotonously decreases on [α₀, +∞). Moreover, since

, we have

by (3.11). Then,

is monotonously decreasing on [α₀, +∞). Thus, to prove (3.10), it is only needed to show that there exists a positive real

such that

()

which implies that

is strictly monotonously decreasing on

Suppose that

()

at a point α₁ ≥ α₀. Since

and

, the equation

holds for some subscript r, which means that

. By positive definiteness of

, we have

and

. One can verify that

on (α₁, +∞) since its monotonicity. Obviously, it is very easy to hold (3.12) if there does not exist α satisfying (3.13). Consequently, there always exists a positive real

such that

is strictly monotonously decreasing on

. It leads to the conclusion (3.10).

Since P^d : 𝒮 → ℛ is concave and the condition (3.10) holds, if (3.9) holds, then the canonical dual function P^d(ρ) is coercive on the open convex set 𝒮. Therefore, the canonical dual problem (P^d) has one maximizer by the theory of convex analysis [4, 18]. This completes the proof.

Clearly, when ∇²P(x) > 0 on 𝒳_a, the dual feasible space 𝒮 is equivalent to and Diag(ρ) ∈ ℛ^n×n by (2.1). Notice that for any given . Then P^d(ρ) is concave and coercive on , and (P^d) has at least one maximizer on . In this case, it is then of interest to characterize a unique solution of (𝒫) by the dual variable.

Let

()

Theorem 3.4. If ∇²P(x) > 0 on 𝒳_a, the primal problem (𝒫) has a unique global minimizer determined by satisfying

()

Proof. To prove Theorem 3.4, by Theorem 2.3 and 3.1, it is only needed to prove that is a KKT point of (P^d) in . By (3.14), the relations for all i ∈ I also hold. Since satisfies equations for all i ∈ J, we can verify that stays in 𝒳_a and the complementarity conditions hold. Thus, is a KKT point of (P^d) in by (2.9), (2.15), and is a unique global minimizer of (𝒫). This completes the proof.

Before beginning of applications to optimal control problems, we present two examples to find global minimizers by differential flows.

Example 3.5. As a particular example of (𝒫), let us consider the following one dimensional nonconvex minimization problem with a box:

()

We have P^′(x) = x² + 2 and P^′′(x) = 2x, for all x² ≤ 1. By choosing

, we solve the following equation in {x² ≤ 1}:

()

to get a solution

. Next we solve the following boundary value problem of the ordinary differential equation:

()

To find a parameter such that

()

we get

()

which satisfies

()

Let x(3) be denoted by

. To find the value of

, we compute the solution of the following algebra equation:

()

and get

. It follows from Theorem 3.1 that

is a global minimizer of Example 3.5.

Remark 3.6. In this example, we see that a differential flow is useful in solving a nonconvex optimization problem. For the global optimization problem, people usually compute the global minimizer numerically. Even in using canonical duality method, one has to solve a canonical dual problem numerically. Nevertheless, the differential flow directs us to a new way for finding a global minimizer. Particularly, one may expect an exact solution of the problem provided that the corresponding differential equation has an analytic solution.

Example 3.7. Given a symmetric matrix A ∈ ℛ^n×n and a vector c ∈ ℛⁿ. Let P(x) = (1/2)x^TAx − c^Tx. We consider the following box-constrained nonconvex global optimization:

()

Since A is an indefinite matrix, we choose a large ρ^* ∈ ℛⁿ such that A + Diag(ρ^*) > 0 and

. We see that the differential equation is

()

where 𝒮 = {ρ ≥ 0∣A + Diag(ρ) > 0}. It leads a differential flow

()

For simplicity without generality, we assume that

and

. If for ρ, det [A + Diag(ρ)] ≠ 0, we have

()

Then the dual problem can be formulated as

()

If we choose a₁ = −0.5, a₂ = −0.5, a₃ = −0.3, c₁ = c₂ = 0.3 and ℓ₁ = 0.5, ℓ₂ = 2, this dual problem has only one KKT point . By Theorem 3.1, is a global minimizer of Example 3.7 and P(1,2) = −2.75 = P^d(1.8,0.7).

4. Applications to Constrained Optimal Control Problems

In this section, we consider the following constrained linear-quadratic optimal control problem:

()

where Q ∈ ℛ^n×n, R ∈ ℛ^m×m are positive semidefinite and positive definite symmetric matrices respectively, x(t) ∈ ℛⁿ is a state vector, and u(t) ∈ ℛ^m is integrable or piecewise continuous on [0, T] within U. Simply, U = {u ∈ ℛ^m | − 1 ≤ u_i ≤ 1}, and U is a unit box. Problems of the above type arise naturally in system science and engineering with wide applications [19, 20].

It is well known that the central result in the optimal control theory is the Pontryagin maximum principle providing necessary conditions for optimality in very general optimal control problems.

4.1. Pontryagin Maximum Principle

Define the Hamilton-Jacobi-Bellman function

()

If the control

is an optimal solution for the problem (4.1), with

and

denoting the state and costate corresponding to

, respectively, then

is an extremal control, that is, we have

()

and a.e. t ∈ [0, T],

()

Unfortunately, above conditions are not, in general, sufficient for optimality. In such a case, we need to go through the process of comparing all the candidates for optimality that the necessary conditions produce, and picking out an optimal solution to the problem. Nevertheless, Lemma 4.1 can prove that the solution satisfies sufficiency conditions of the type considered in this section, then these conditions will ensure the optimality of the solution.

Lemma 4.1. Let be an admissible control, and be the corresponding state and costate. If , , and satisfy the Pontryagin maximum principle ((4.3)-(4.4)), then is an optimal control to the problem (4.1).

Proof. For any given x, λ, let

()

For any u ∈ U, by the definition of H^*, H^*(x, λ) ≤ H(x, u, λ), and H^*(x, λ) is equivalent to the following global optimization

()

Moreover, we can derive an analytic form of the global minimizer for (4.6) via the co-state λ. It is easy to see that the minimizer

of (4.6) doesn′t depend on x, that is,

which implies that

()

Since U is a closed convex set, by the classical linear systems theory, the state set X of (4.1) is a convex subset of ℛⁿ. By the fact that the minimizer

does not depend on x and the convexity of the integrand in the cost functional, the function H^*(x, λ) is convex with respect to x over X. In other words, for any x ∈ X, and a.e. t ∈ [0, T],

()

Thus, for any admissible pair (x(·), u(·)), and a.e. t ∈ [0, T], by (4.5), we have

()

which leads to

()

Notice that

and

. We can obtain

()

This means that J attains its minimum at

. The proof is completed.

Lemma 4.1 reformulates the constrained optimal control problem (4.1) into a global optimization problem (4.6). Based on Theorem 3.4, an analytic solution of (4.1) can be expressed via the co-state.

Theorem 4.2. Suppose that

()

We have the following expression

()

where ρ(λ) with respect to the co-state λ is given by ρ(λ) ≥ 0 satisfying

()

Proof. The proof of Theorem 4.2 is parallel to Theorem 3.4.

Substituting u = −[R + Diag(ρ(λ))] ⁻¹B^Tλ into (4.3), we have

()

is a solution of the above equations (4.15), let

()

By Lemma 4.1,

satisfy the Pontryagin maximum principle, and we present an analytic form of the optimal control to (4.1) via the canonical dual variable

()

Next, we give an example to illustrate our results.

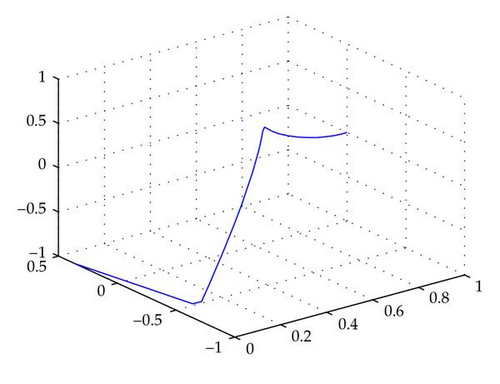
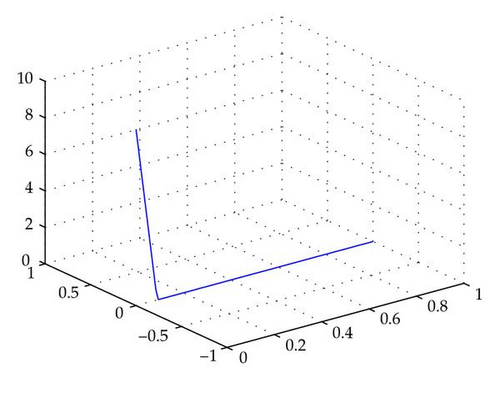
Example 4.3. We consider

()

and T = 1 in (4.1). Q ≥ 0 and R > 0 satisfy the assumption in (4.1).

Following the idea of Lemma 4.1 and Theorem 4.2, we need to solve the following boundary value problem for differential equations to derive the optimal solution

()

By solving equations (4.19) in MATLAB, we can obtain the optimal control

and the dual variable

as follows (see Figures 1 and 2).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The optimal control in Example 4.3.

Acknowledgments

The authors would like to thank the referees for their helpful comments on the early version of this paper. This work was supported by the National Natural Science Foundation of China (no. 10971053).

References

1 Floudas C. A., Deterministic Global Optimization: Theory, Methods and Applications, 2000, 37, Kluwer Academic Publishers, Dordrecht, The Netherlands, Nonconvex Optimization and Its Applications, 1746644.
10.1007/978-1-4757-4949-6
Google Scholar
2 Gao D. Y., Nonconvex semi-linear problems and canonical duality solutions, Advances in Mechanics and Mathematics. Vol. II, 2003, 4, Kluwer Academic Publishers, Boston, Mass, USA, 261–312, Adv. Mech. Math., 2058481.
10.1007/978-1-4613-0247-6_5
Google Scholar
3 Fang S.-C., Gao D. Y., Sheu R.-L., and Wu S.-Y., Canonical dual approach to solving 0-1 quadratic programming problems, Journal of Industrial and Management Optimization. (2008) 4, no. 1, 125–142, 2379923, ZBL1180.90195.
10.3934/jimo.2008.4.125
Web of Science® Google Scholar
4 Rockafellar R. T., Convex Analysis, 1970, Princeton University Press, Princeton, NJ, USA, Princeton Mathematical Series, No. 28, 0274683.
10.1515/9781400873173
Google Scholar
5 Gao D. Y., Solutions and optimality criteria to box constrained nonconvex minimization problems, Journal of Industrial and Management Optimization. (2007) 3, no. 2, 293–304, 2329373, ZBL1171.90504.
10.3934/jimo.2007.3.293
Web of Science® Google Scholar
6 Gao D. Y. and Ruan N., Solutions to quadratic minimization problems with box and integer constraints, Journal of Global Optimization. (2010) 47, no. 3, 463–484, https://doi.org/10.1007/s10898-009-9469-0, 2657942.
10.1007/s10898-009-9469-0
Web of Science® Google Scholar
7 Wang Z., Fang S.-C., Gao D. Y., and Xing W., Global extremal conditions for multi-integer quadratic programming, Journal of Industrial and Management Optimization. (2008) 4, no. 2, 213–225, 2386071, ZBL1161.90457.
10.3934/jimo.2008.4.213
Web of Science® Google Scholar
8 Gao D. Y., Perfect duality theory and complete solutions to a class of global optimization problems, Optimization. (2003) 52, no. 4-5, 467–493, https://doi.org/10.1080/02331930310001611501, 2039234.
10.1080/02331930310001611501
Web of Science® Google Scholar
9 Gao D. Y., Duality Principles in Nonconvex Systems: Theory, Methods and Applications, 2000, 39, Kluwer Academic Publishers, Dordrecht, The Netherlands, Nonconvex Optimization and Its Applications, 1773838.
10.1007/978-1-4757-3176-7
Google Scholar
10 Gao D. Y., Canonical dual transformation method and generalized triality theory in nonsmooth global optimizaton, Journal of Global Optimization. (2000) 17, no. 1–4, 127–160, https://doi.org/10.1023/A:1026537630859, 1807971.
10.1023/A:1026537630859
Web of Science® Google Scholar
11 Adjiman C. S., Dallwig S., Floudas C. A., and Neumaier A., A global optimization method, αBB, for general twice-differentiable constrained NLPs-I. Theoretical advances, Computers and Chemical Engineering. (1998) 22, no. 9, 1137–1158, https://doi.org/10.1016/S0098-1354(98)00027-1.
10.1016/S0098-1354(98)00027-1
CAS Web of Science® Google Scholar
12 Adjiman C. S., Androulakis I. P., and Floudas C. A., A global optimization method, αBB, for general twice-differentiabe constrained NLPs-II. Implementation and computational results, Computers and Chemical Engineering. (1998) 22, no. 9, 1159–1179, https://doi.org/10.1016/S0098-1354(98)00218-X.
10.1016/S0098-1354(98)00218-X
CAS Web of Science® Google Scholar
13 Grassmann H., Extension Theory, 2000, 19, American Mathematical Society, Providence, RI, USA, History of Mathematics, 1747519.
10.1090/hmath/019
Google Scholar
14 Rota G. C., Extension theory of differential operators. I, Communications on Pure and Applied Mathematics. (1958) 11, 23–65, 0096852, https://doi.org/10.1002/cpa.3160110103, ZBL0088.06303.
10.1002/cpa.3160110103
Web of Science® Google Scholar
15 Adjiman C. S., Androulakis I. P., and Floudas C. A., Global optimization of mixed-integer nonlinear problems, AIChE Journal. (2000) 46, no. 9, 1769–1797.
10.1002/aic.690460908
CAS Web of Science® Google Scholar
16 Mönnigmann M., Efficient calculation of bounds on spectra of Hessian matrices, SIAM Journal on Scientific Computing. (2008) 30, no. 5, 2340–2357, 2429469, https://doi.org/10.1137/070704186, ZBL1181.65055.
10.1137/070704186
Web of Science® Google Scholar
17 Hertz D., Adjiman C. S., and Floudas C. A., [email protected], Two results on bounding the roots of interval polynomials, Computers and Chemical Engineering. (1999) 23, no. 9, 1333–1339, https://doi.org/10.1016/S0098-1354(99)00292-6.
10.1016/S0098-1354(99)00292-6
CAS Web of Science® Google Scholar
18 Ekeland I. and Temam R., Convex Analysis and Variational Problems, 1976, North-Holland, Amsterdam, The Netherlands, 0463994.
Google Scholar
19 Casti J., The linear-quadratic control problem: some recent results and outstanding problems, SIAM Review. (1980) 22, no. 4, 459–485, https://doi.org/10.1137/1022089, 593859, ZBL0452.49003.
10.1137/1022089
Web of Science® Google Scholar
20 Robinson C., Dynamical Systems: Stability, Symbolic Dynamics, and Chaos, 1995, CRC Press, Boca Raton, Fla, USA, Studies in Advanced Mathematics, 1396532.
Google Scholar

Citing Literature

All articles

Complete Solutions to General Box-Constrained Global Optimization Problems

Abstract

1. Introduction

2. A Differential Flow and Canonical Dual Problem

3. Complete Solutions to Global Optimization Problems

4. Applications to Constrained Optimal Control Problems

4.1. Pontryagin Maximum Principle

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Complete Solutions to General Box-Constrained Global Optimization Problems

Abstract

1. Introduction

2. A Differential Flow and Canonical Dual Problem

3. Complete Solutions to Global Optimization Problems

4. Applications to Constrained Optimal Control Problems

4.1. Pontryagin Maximum Principle

Acknowledgments

References

Citing Literature

Figures

References

Related

Information