Advances in Mathematical Physics
Volume 2011, Issue 1 365085
Research Article
Open Access

The C-Version Segal-Bargmann Transform for Finite Coxeter Groups Defined by the Restriction Principle

Stephen Bruce Sontz, 

Corresponding Author

Stephen Bruce Sontz

Centro de Investigación en Matemáticas, A.C. (CIMAT), 36240 Guanajuato, GTO, Mexico cimat.mx

Search for more papers by this author
First published: 25 December 2011
https://doi.org/10.1155/2011/365085
Citations: 1
Academic Editor: N. Kamran

Abstract

We apply a special case, the restriction principle (for which we give a definition simpler than the usual one), of a basic result in functional analysis (the polar decomposition of an operator) in order to define Cμ,t, the C-version of the Segal-Bargmann transform, associated with a finite Coxeter group acting in ℝN and a given value t > 0 of Planck′s constant, where μ is a multiplicity function on the roots defining the Coxeter group. Then we immediately prove that Cμ,t is a unitary isomorphism. To accomplish this we identify the reproducing kernel function of the appropriate Hilbert space of holomorphic functions. As a consequence we prove that the Segal-Bargmann transforms for Versions A, B, and D are also unitary isomorphisms though not by a direct application of the restriction principle. The point is that the C-version is the only version where a restriction principle, in our definition of this method, applies directly. This reinforces the idea that the C-version is the most fundamental, most natural version of the Segal-Bargmann transform.

1. Introduction

The basic idea involved in the restriction principle is the use of the polar decomposition of an operator in order to define a unitary transformation. The polar decomposition (e.g., see [1, 2]) is a well-known result in functional analysis that says that one can write T = U|T|, where and U is a partial isometry. Here T is a closed (possibly unbounded), densely defined linear operator mapping its domain Dom (T) ⊂ ℋ1 to ℋ2, where ℋ1 and ℋ2 are complex Hilbert spaces. It turns out that is the positive square root of the densely defined self-adjoint operator T*T and so maps a domain in ℋ1 to ℋ1. The partial isometry U maps ℋ1 to ℋ2. We are generally interested in the case when the partial isometry U is a unitary isomorphism from ℋ1 onto ℋ2, which is true if and only if T is one-to-one and has dense range.

Applying the polar decomposition theorem as a means for constructing unitary operators is a very general method. Also this method has nothing to do with the structures of the complex Hilbert spaces ℋ1 and ℋ2. And these can be advantages or disadvantages depending on one′s particular interest.

But if we assume that ℋ2 is some set of complex-valued functions (and in general not equivalence classes of functions) on a set X and ℋ1 is a Hilbert space of complex-valued functions (or possibly equivalence classes of functions) on a subset M of X, then we define the restriction operator R : ℋ2 → ℋ1 by Rf(x) : = f(x) for all f ∈ ℋ2 and all x ∈ M. This is at a formal level only, since in general, we do not know that Rf  ( = f↾M = f restricted to M) is an element of ℋ1. Then we apply the polar decomposition to the adjoint R* of the restriction operator R (provided that R* is a closed, densely defined operator) to get R* = UP, where P is a positive operator of no further interest and U is a partial isometry from ℋ1 to ℋ2. We say that U is defined by the restriction principle. We then have to show that R* is one-to-one and has dense range in order to prove that the partial isometry U is a unitary isomorphism from ℋ1 onto ℋ2, this being the case of interest for us. In this paper ℋ2 will be a reproducing kernel Hilbert space. This turns out to be quite useful for deriving explicit formulas, but it is not a necessary aspect of this approach.

We note that our definitions here differ from those of other authors. For us a restriction operator is simply restriction to a subset and nothing else. Other authors allow for operators that are the composition of restriction to a subset followed or preceded by another operator, often a multiplication operator. Then these authors apply the polar decomposition to these more general “restriction” operators. Now this introduces another operator as a deus ex machina; that is, something that arrives on the stage without rhyme or reason but that saves the day by making everything work out well. We object to such an approach to constructing a mathematical theory on general principles, both aesthetic and logical. Moreover, in the context of generalizations of Segal-Bargmann analysis it seems that the application of the restriction principle (using our definition of this) in the context of the C-version of Segal-Bargmann analysis eliminates any need to introduce unmotivated factors. This is clearly seen in this paper as well as in [3, 4]. Also, as we will see, developing the theory first for the C-version gives us enough information to dispose easily of the other versions, including an explanation of where the “mysterious” multiplication factors come from for the A, B, and D versions. See Hall [5] for the original use of this nomenclature of “versions” and [6] for its use in the context of finite Coxeter groups.

When the above sketch can be filled in rigorously, this is a simple way of defining a unitary isomorphism U. Moreover, the simplicity of the definition often allows one to prove results about U in a straightforward way. However, the devil lies in the details as the saying goes, and the details can sabotage this approach. For example, the definition of the restriction operator R might not make sense on the domain ℋ2 though it always makes sense on the subspace Dom (R) : = {f ∈ ℋ2∣Rf = f↾M ∈ ℋ1}. However, it could happen that Dom (R) is the zero subspace, in which case this method is for naught.

The full history of this method is not our primary interest, but we present what we know about this in the area of mathematical physics and related areas of analysis. In this paragraph, and only in this paragraph, the phrase “restriction principle” is used in the sense of the authors cited. Peetre and Zhang in 1992 in [7] used polar decomposition to get the Berezin transform. A polar decomposition was used by Ørsted and Zhang in [8] in order to define and study the Weyl transform. The article [4] by Ólafsson and Ørsted contains some applications of restriction principles in order to understand the work of Hall in [5] and Hijab in [9]. The approach in [4] was recently followed up by Hilgert and Zhang in [3] in their study of compact Lie groups. Also Davidson et al. used a restriction principle in [10] in order to study Laguerre polynomials. See [10] for more references on this topic and on the Berezin transform. Zhang in [11] used a restriction principle to study the Segal-Bargmann transform of a weighted Bergman space on a bounded symmetric domain. In [12] a restriction principle was used by Ben Saïd and Ørsted to produce a “generalized Segal-Bargmann transform” associated with a finite Coxeter group acting on ℝN. We first learned about this method by reading [8] within some six months of its publication. But our recent interest was stimulated by our desire to understand [12].

We should note that the same generalized Segal-Bargmann space as found in [12] together with its associated Segal-Bargmann transform (but called the chaotic transform) can be found for the case M = ℝ, X = ℂ (dimension N = 1) in Sifi and Soltani [13] and for M = ℝN, X = ℂN (arbitrary finite dimension N) in Soltani [14]. However, neither [13] nor [14] used a restriction principle. The case M = ℝ, X = ℂ is discussed by us in [15] and in the references found there, while we studied the arbitrary finite dimensional case M = ℝN, X = ℂN in [6]. Our point of view in [6, 15] was to use the approach of Hall [5], which is directly based on heat kernel analysis, rather than using the restriction principle. While the restriction principle can be considered as an alternative to the approach of Hall, this approach still relies in an essential way, at least in this paper, on the heat kernel of the Dunkl theory as we will see.

The restriction principle approach has various limitations. For example, X and M need not be manifolds and even if they are, X need not be the cotangent bundle of M so that the theory can lose contact with physics and symplectic geometry. Also, the Hilbert spaces are not constructed, but they must be known prior to applying this approach. And there is no necessary connection with heat kernel analysis. Of course, these attributes can be viewed as strengths rather than weaknesses, since they could allow for more general application than other approaches.

In this paper we will use the restriction principle to define the C version of the Segal-Bargmann transform Cμ,t associated with a finite Coxeter group acting on ℝN and with a value t > 0 of Planck′s constant. (We will discuss the multiplicity function μ later on.) We also show that Cμ,t is a unitary isomorphism. This is a new way to construct Cμ,t and prove that it is a unitary isomorphism. Along the way we have to find an explicit formula for the reproducing kernel function for the Hilbert space 𝒞μ,t that turns out to be the range of the unitary transform Cμ,t.

A major point of this paper is that our original proof of the unitarity of the transform Cμ,t, as given in [6], depends on using the previously established unitarity of Aμ,t, the A-version of the Segal-Bargmann transform. Since none of the versions of the Segal-Bargmann transform appears as the most natural version in the analysis given in [6], there is no logical reason to start with the A-version. However, using that approach, things in the end do work out quite nicely. But the proof given here seems to us to be more natural, since the starting point, namely the C-version, plays a distinguished role, while the remaining versions are obtained as secondary constructs.

Having established these results in the C-version, it is then simple for us to prove the corresponding results for Versions A, B, and D. In particular we show as an immediate consequence of our work how the “restriction” operator used in [12] (which is actually restriction followed by multiplication by an unmotivated factor) arises in a natural way from our restriction operator, which is simply restriction without multiplication by some fudge factor.

The upshot is that the restriction principle for the C-version can be used as a starting point for defining all of the versions of the Segal-Bargmann transform associated to a finite Coxeter group. Therefore the restriction principle is a fundamental principle in Segal-Bargmann analysis. So, this paper complements the approach in our recent paper [6], where we showed by using the Dunkl heat kernel that the versions A, B, and C of the Segal-Bargmann transform associated with a finite Coxeter group are analogous to the versions of the Segal-Bargmann transform as introduced by Hall in [5], where he used the appropriate heat kernel.

Since many authors now take the C-version to be the most fundamental version of the Segal-Bargmann transform, we feel that our result has an impact on that approach to this field of research. We also feel that the current approach is better than that in [6], since we now emphasize how the C-version is singled out in yet another way as more fundamental than the other versions.

2. Definitions and Other Preliminaries

We follow the definitions and notation of [6]. Consult [6] and the references given there for a more leisurely review of this material. In that paper we studied various versions of the Segal-Bargmann transform associated with a finite Coxeter group acting on the Euclidean space ℝN. One of these versions (known as Version A or the A-version) is, as we will see, a unitary isomorphism of Hilbert spaces
(2.1)
where the density function (with respect to Lebesgue measure) for q ∈ ℝn is
(2.2)
Throughout this paper we let t > 0 denote Planck′s constant. Here the Macdonald-Mehta-Selberg constant is defined by
(2.3)
(In a moment we will discuss γμ, the finite set ℛ and μ : ℛ → [0, ∞).) Since this integral does not depend on the value of t > 0 (by dilating), we do not include this parameter in the notation on the left side. Clearly, 0 < cμ < ∞.
We define the Version A Segal-Bargmann transform as the integral kernel operator
(2.4)
for ψ ∈ L2(ℝN, ωμ,t) and z ∈ ℂN and t > 0, where the integral kernel is defined for z ∈ ℂN and q ∈ ℝN by
(2.5)
where (given that z = (z1, …, zN)) is a holomorphic function and q2 : = ∥q∥2 is the usual Euclidean norm squared. The function Eμ : ℂN × ℂN → ℂ will be introduced momentarily. Using (2.9) below and the Cauchy-Schwarz inequality one shows the absolute convergence of the integral in (2.4). Our paper [6] provides motivation for formula (2.5).
In the above ℛ is a certain finite subset of ℝN, known as a root system, μ : ℛ → [0, ∞) is a multiplicity function (see [6] for definitions) and
(2.6)
It may be possible to weaken the hypothesis μ ≥ 0 that we are imposing here while still having the same results. We work with a fixed root system ℛ and a fixed multiplicity function μ throughout this paper. See [6] for the details about how ℛ gives rise to a finite Coxeter group acting as orthogonal transformations of ℝN.
The space ℬμ,t introduced above ([12, 14]), which is called the Version A Segal-Bargmann space, is the reproducing kernel Hilbert space of holomorphic functions f : ℂN → ℂ whose reproducing kernel Kμ,t : ℂN × ℂN → ℂ is defined for z, w ∈ ℂN and t > 0 by
(2.7)
where Eμ is the Dunkl kernel function associated with the Coxeter group (associated itself to the root system ℛ) and the multiplicity function μ. For any z = (z1, …, zN) ∈ ℂN, we let denote its complex conjugate. The Dunkl kernel Eμ : ℂN × ℂN → ℂ (see [16–18]) is a holomorphic function with many properties. We simply note for now that
(2.8)
for all λ ∈ ℂ and all z, w ∈ ℂN. In the first equation 0 denotes the zero vector in ℂN. Also, z · w = ∑jzjwj in the obvious notation. We will also be using the estimate (see [19])
(2.9)
for all z, w ∈ ℂN, which holds if μ ≥ 0. (Here, ∥z∥ is the Euclidean norm of z ∈ ℂN. Also recall that μ ≥ 0 is assumed throughout this paper.)

For a Hilbert space ℋ we use the notations 〈·,·〉ℋ and ∥·∥ℋ for its inner product and norm, respectively. The inner product is antilinear in its first argument, linear in its second. All Hilbert spaces considered are over the field of complex numbers.

We will be using dilations. Our present notation for these operators is Dλψ(x) : = ψ(λx), where ψ is a function in some appropriate function space. The proof of the next result is straightforward and so is left to the reader.

Lemma 2.1. For every λ > 0 and t > 0, we have that

(2.10)
is a unitary isomorphism.

Finally, we want to introduce the Dunkl heat kernel (see [18, 19]) for the heat equation associated with the Dunkl Laplacian Δμ; namely
(2.11)
The Dunkl Laplacian Δμ is defined and discussed in [19]. In particular, it has a realization in L2(ℝN, ωμ,t) as an unbounded, self-adjoint operator with Δμ ≤ 0 and spectrum (−∞, 0]. Specifically, we have for t > 0 and x ∈ ℝN that
(2.12)
solves (2.11) for any initial condition f ∈ L2(ℝN, ωμ,t) (see [18] for more details), where the Dunkl heat kernel  ρμ,t : ℝN × ℝN → ℝ is given for all x, q ∈ ℝN and t > 0 by
(2.13)
This has an analytic extension ℂN × ℂN → ℂ, which we also denote as ρμ,t. One of the basic results of [6] is that for z ∈ ℂN and q ∈ ℝN we have
(2.14)
which, in accordance with the approach of Hall [5], indicates that (2.4) is justifiably called the Version A Segal-Bargmann transform associated with a finite Coxeter group. This formula also clarifies the nature of the seemingly arbitrary definition (2.5) of the kernel function of the integral transform Aμ,t.
Notice that the reproducing kernel function for ℬμ,t clearly satisfies
(2.15)
This identity shows that the reproducing kernel function for the Hilbert space ℬμ,t is determined by the Dunkl heat kernel ρμ,t. Or, in other words, we can get the Segal-Bargmann space for Version A from the Dunkl heat kernel. Another way to write this reproducing kernel in terms of the Dunkl heat kernel ρμ,t is to consider equation (46) in Hall [5]. In the present context the analogous result says that for all z, w ∈ ℂN we have
(2.16)
as the reader can check. (Hint: one needs an identity involving the Dunkl kernel. See [12, Equation (2.5)], or [18, Proposition 2.37, equation (2)].) Even though we will not be using these two formulas for Kμ,t(z, w), we present them to show how the Dunkl heat kernel determines the reproducing kernel of ℬμ,t. As we will show later, the reproducing kernel function for the Version C Segal-Bargmann space is also determined by the Dunkl heat kernel ρμ,2t.

We gather here some basic results of functional analysis that we will be using. (See [1], especially Chapter III, Section 5 and Chapter V, Section  3, for more details.) Let ℋ1 and ℋ2 be complex Hilbert spaces with T : Dom (T) → ℋ2 a linear operator which is densely defined (which means Dom (T) is a dense subspace in ℋ1). Let T* denote the adjoint of T. If T is closable (namely, has a closure), then we denote the closure of T by . We denote the kernel and range of T by Ker   T and Ran  T, respectively. We say that T is globally defined if Dom (T) = ℋ1. For any subset A in a Hilbert space, is its closure in the norm topology and A⊥ is its orthogonal complement. The following proposition comes from elementary functional analysis.

Proposition 2.2. Let T : Dom (T) → ℋ2 be densely defined, as above. Then we have the following:

  • (1)

    if T is closable, then T* is closed, densely defined and ,

  • (2)

    Ker  T* = (Ran  T)⊥,

  • (3)

    if T is closed, then ,

  • (4)

    if T is bounded (i.e., there exists C ≥ 0 such that for all ϕ ∈ Dom (T)), then T is closable and is globally defined and bounded (with the same bound as T). In particular, if T is bounded and closed, then T is globally defined, that is, Dom (T) = ℋ1.

As we have already mentioned, we will use a standard result of functional analysis known as the polar decomposition of an operator. For the reader′s convenience we state this result. We present a modification of the statement of Theorem VIII.32 in [2]. A very thorough discussion of this topic is also given in [1]. (See Chapter VI, Section 2.7.) We state this theorem for a closed densely defined linear operator (that is, it may be bounded or not).

Theorem 2.3 (Polar Decomposition). Let ℋ1 and ℋ2 be Hilbert spaces and A : Dom (A) → ℋ2 be a closed linear operator, defined in the dense linear domain Dom (A) ⊂ ℋ1. Then there exists a positive self-adjoint operator with Dom (|A|) = Dom (A) and there exists a partial isometry U : ℋ1 → ℋ2 with initial space (Ker   U)⊥ = (Ker   A)⊥ and final space such that

(2.17)
on their common domain Dom (A) = Dom (|A|). Also, U and |A| are uniquely determined by Ker   |A| = Ker   A and the above properties.

In particular, U is one-to-one if and only if Ker   A = 0, while U is onto if and only if Ran  A is dense.

Consequently, U is a unitary isomorphism of ℋ1 onto ℋ2 if and only if Ker   A = 0 and Ran  A is dense.

Remarks 2.4. Theorem 2.3 is stated in terms of the structures of Hilbert spaces, nothing else. So it is invariant under unitary isomorphisms. To make this more explicit we suppose Fj : ℋj → 𝒦j are unitary isomorphisms for j = 1,2, where 𝒦1 and 𝒦2 are Hilbert spaces. (We continue using the notation of Theorem 2.3.) Then define Dom (B) : = F1(Dom (A)), a subset of 𝒦1, and B : Dom (B) → 𝒦2 by . Clearly, B is a closed, densely defined operator. So, according to Theorem 2.3, we have that B = V|B|, where and V : 𝒦1 → 𝒦2 is a uniquely determined partial isometry. Then the relation of the polar decomposition of B with that of A = U|A| is

(2.18)
Moreover, if A = R* where R is a restriction operator, then according to our definition U is defined by a restriction principle. Nonetheless, V need not be defined by a restriction principle; that is, B need not be the adjoint of a restriction operator even though A is. However, V is well defined by polar decomposition. While the restriction principle is not a unitary invariant, this discussion shows that there is a straightforward method for transforming a polar decomposition by unitary transformations. There is absolutely no guesswork involved.

It seems to be a rule of thumb in Segal-Bargmann analysis that it is rather straightforward to prove that a Segal-Bargmann transform is injective, while to prove that it is surjective requires a rather detailed argument. However, that is not so for the restriction principle we will consider. On the contrary, as we will see in the next section, proving that the transform is surjective is immediate (using uniqueness of analytic continuation), while proving that it is injective does involve a bit more work (using that the Dunkl transform, to be discussed later, is injective) though is not all that difficult.

3. Version C

In this section we will show how Version C of the Segal-Bargmann transform associated to a Coxeter group arises from the restriction principle. We feel that using the restriction principle is a more fundamental approach to this theory.

We recall from [6] that the Version C (or C-version) Segal-Bargmann transform for ψ ∈ L2(ℝN, ωμ,t) and z ∈ ℂN is defined by
(3.1)
where Cμ,t(z, q) : = ρμ,t(z, q). This integral converges absolutely by using the estimate (2.9). This definition is the natural analogue in this context of the definition of the C-version given in [5]. Then we proved in [6] that this gives a unitary isomorphism
(3.2)
The definition of the Hilbert space 𝒞μ,t of holomorphic functions will be given below. Other details may be found in [6]. First, we will identify the reproducing kernel function for this Hilbert space. But we want this space to be the image of the coherent state transform Cμ,t, and it is well known in the theory of coherent states that the reproducing kernel in the codomain Hilbert space (if it exists) is necessarily given by the inner product in the domain Hilbert space of two coherent states. In this context that will be
(3.3)
which can be calculated to give the formula for Lμ,t in the next theorem. Essentially, this involves the time evolution for the time interval t of the heat kernel at time t. This is why the result is (given our conventions, proportional to) the heat kernel at time 2t. An important point here is that there is no liberty in the choice for this reproducing kernel, but rather it results from evaluating an integral.

We again call to the reader′s attention that restriction principles do not define the Hilbert spaces, which must be introduced prior to the application of a restriction principle. And so it is in the present case with the Hilbert space 𝒞μ,t.

Theorem 3.1. The reproducing kernel function Lμ,t for the Hilbert space 𝒞μ,t is given by

(3.4)
for all z, w ∈ ℂN.

Remarks 3.2. Note the similarity of formula (3.4) with the reproducing kernel for the Version C generalized Segal-Bargmann space for compact, connected Lie groups as given by Hall in [5] (Theorem 6, page 127):

(3.5)
See [5] for the definition of this notation and further details. Also, note that this formula occurs in Segal-Bargmann analysis in the context of Heisenberg groups in [20] and in the context of the compact Heckman-Opdam setting in [21]. Admittedly, the factors of 2 in our formula look strange and are not found in these references. These factors are a consequence of the unusual convention we have introduced in [6] for normalizing the Dunkl heat kernel ρμ,t and the measure dωμ,t.

Proof. We let ℋ(ℂN) denote the space of all of the holomorphic functions f : ℂN → ℂ. We recall three definitions from [6]. For f ∈ ℋ(ℂN) we define Gf ∈ ℋ(ℂN) by

(3.6)
for all w ∈ ℂN. (Note that Aμ,2t(2w, 0) = exp (−w2/t) is never zero.) Then we define
(3.7)
which becomes a Hilbert space with its inner product defined by
(3.8)
for f1, f2 ∈ 𝒞μ,t.

The reproducing kernel of a Hilbert space must satisfy two characteristic properties. The first of these is that must be an element in the Hilbert space 𝒞μ,t. The second is that for all f ∈ 𝒞μ,t and z ∈ ℂN.

We start with the first property. Now Lz ∈ 𝒞μ,t if and only if

(3.9)
is an element of ℬμ,t/2 as a function of w ∈ ℂN.

So we calculate

(3.10)
Here Kμ,t/2 is the reproducing kernel function for the Hilbert space ℬμ,t/2, which implies that Kμ,t/2(z/2,   ·) ∈ ℬμ,t/2 for all z ∈ ℂN and so GLz ∈ ℬμ,t/2 as desired.

Now for the second property we evaluate the right side for f ∈ 𝒞μ,t (which implies Gf ∈ ℬμ,t/2) and use GLz ∈ ℬμ,t/2 to get

(3.11)
for all z ∈ ℂN. So the second property has also been established, thereby completing the proof without ever using the transform Cμ,t.

The definition of the Hilbert space 𝒞μ,t given in (3.6), (3.7), and (3.8) is what we were naturally led to while preparing [6]. It is the range space of the Version C Segal-Bargmann transform Cμ,t introduced there. However, the result of Theorem 3.1 gives us an intrinsic way of defining 𝒞μ,t, namely as the Hilbert space of holomorphic functions f : ℂN → ℂ with reproducing kernel defined by (3.4). This is arguably a better approach. However, the natural way to do this would be to omit the factors of 2 from (3.4). This would simply give us a different normalization of the Version C of the Segal-Bargmann space. But either way the Hilbert space 𝒞μ,t must be defined before applying a restriction principle, as we noted earlier.

Of course, in order to apply the restriction principle, we need to define the restriction operator rigorously.

Definition 3.3. We define the restriction operator

(3.12)
by
(3.13)
for all f in a domain Dom (Rμ,t) ⊂ 𝒞μ,t and all x ∈ ℝN. The definition of the domain of Rμ,t in 𝒞μ,t is the obvious one
(3.14)
Note that Rμ,t does depend on μ and t, since these parameters appear in both the domain and codomain spaces of this operator.

We will show later on that Rμ,t is a globally defined, bounded operator. Still this is a bit surprising since the following standard estimates do not prove it. Indeed, for any 0 ≠ f ∈ Dom (Rμ,t) ⊂ 𝒞μ,t we have that

(3.15)
Here we used (2.9) in the second inequality and the usual pointwise estimate for functions in a reproducing kernel Hilbert space in the first inequality.

As far as we know at this point of our exposition it could well be the case that Dom (Rμ,t) = 0. We now show that this domain is actually dense along with other properties of Rμ,t.

Theorem 3.4. The operator R ≡ Rμ,t defined on its domain Dom (Rμ,t) is a closed, densely defined operator that is one-to-one and has dense range in L2(ℝN, ωμ,t). Also its adjoint is densely defined, closed, one-to-one and has dense range. In particular, we have that Lz ∈ Dom (Rμ,t) for all z ∈ ℂN.

Proof. By the uniqueness of analytic continuation from ℝN to ℂN, we have immediately that Rμ,t is one-to-one, that is, Ker   Rμ,t = 0.

We claim that the functions Lz ∈ 𝒞μ,t are all in Dom (R). This follows from

(3.16)
for z ∈ ℂN and x ∈ ℝN, which (using μ ≥ 0 and (2.9)) gives the estimate
(3.17)
This clearly implies that is integrable with respect to the measure dωμ,t(x). And so Lz ∈ Dom (R). Now, by the theory of reproducing kernel Hilbert spaces, the finite linear combinations of the functions Lz with z ∈ ℂN form a dense subspace of 𝒞μ,t and so Dom (R) is dense; that is, R is a densely defined operator.

The proof that the graph of R is closed is a standard argument, which we leave to the reader. So, R is a closed operator.The proof that R* is a densely defined and closed operator follows by applying Proposition 2.2 to the closed operator R.

To prove that is injective, we first find a formula for . So we take ψ ∈ Dom (R*) ⊂ L2(ωμ,t) and z ∈ ℂN with the intention of calculating in general. Introducing the reproducing kernel Lz in the second equality and using Lz ∈ Dom (R) in the third equality we calculate as follows:

(3.18)
Notice how the factors of 2 combined with dωμ,t to form dωμ,2t, which is the measure we want to use in integrals involving the Dunkl heat kernel ρμ,2t.

Now put z = −ix for x ∈ ℝN in (3.18) to get

(3.19)
where ℱμ,2t is the Dunkl transform. (See [16–19] for information on this transform and [6] for our notation and conventions. For this argument, we only need to know that
(3.20)
is injective.) At this point, let us note that ψ ∈ Dom (R*) ⊂ L2(ωμ,t) implies that so that (3.19) makes sense.

We now assume that ψ ∈ Ker   R* ⊂ Dom (R*). So, for all x ∈ ℝN. Using that ℱμ,2t is injective on L2(ωμ,2t), it follows from (3.19) that ψ = 0 almost everywhere with respect to the measure dωμ,2t. Hence ψ = 0 almost everywhere with respect to dωμ,t. This shows that is injective.

To prove that the ranges are dense, we will again use Proposition 2.2. Since Rμ,t is closed we have that and that . The last equality then implies that . (We use the symbol 0 here to designate ambiguously the zero subspace of the appropriate Hilbert space.)

We have shown that the range of the restriction operator Rμ,t is dense only for the sake of completeness. This will not be used later on.

We continue with our main result.

Theorem 3.5 (Restriction principle: Version C). (i) Suppose that the multiplicity function satisfies μ ≥ 0. The restriction principle says that the partial isometry Uμ,t produced by writing the adjoint of the restriction operator, namely , in its polar decomposition; that is,

(3.21)
actually gives a unitary isomorphism Uμ,t : L2(ℝN, ωμ,t) → 𝒞μ,t.

(ii) Moreover, we have that

(3.22)
where Cμ,t is defined by equation (3.1).

So it follows that Cμ,t : L2(ℝN, ωμ,t) → 𝒞μ,t, the C-version of the Segal-Bargmann transform associated with a finite Coxeter group and the value t > 0 of Planck′s constant, is a unitary isomorphism.

Remark 3.6. Instead of using the definition (3.1) from [6], we can use the first part of this theorem to define Cμ,t : = Uμ,t. It is in this sense that the restriction principle can be said to define the C-version of the Segal-Bargmann transform.

Proof. We begin by finding another formula for . So we take ψ ∈ Dom (R*) ⊂ L2(ωμ,t) and z ∈ ℂN. Continuing the calculation given above in (3.18), we obtain

(3.23)
(Parenthetically, we warn the reader that this equation does not say that is equal to . This quite simply can not be true, since the codomains of these two operators are not the same space. The correct statement is that is equal to followed by analytic continuation to ℂN. Also, it is clear that , since the domains of and Cμ,2t are equal as sets.)

To get the polar decomposition of R* we have to analyze the operator R**R*. But , since R is closed. So we consider RR* from now on. By using the definition of R we immediately get for x ∈ ℝN and ψ ∈ Dom   (RR*) that

(3.24)
and so
(3.25)
on Dom   (RR*) which is dense in L2(ℝN, ωμ,t) by a theorem of von Neumann. (See [1], Chapter 5, Section 3, Theorem 3.24, page 275.) But RR* is closed (being self-adjoint by standard functional analysis) and bounded (being a restriction of the bounded operator ) and so is a globally defined, bounded operator by Proposition 2.2. Moreover, on L2(ωμ,t). So, is a globally defined, bounded operator with on L2(ℝN, ωμ,t), since the operator , is globally defined, bounded and its square is .

Next the polar decomposition theorem tells us that

(3.26)
on Dom (R*) = Dom (|R*|), where Uμ,t is partial isometry from L2(ωμ,t) to 𝒞μ,t. But Dom (|R*|) = L2(ωμ,t) and so R* is globally defined and equal by (3.26) to the composition of two bounded operators on L2(ℝN, ωμ,t). Therefore R* is also bounded. Since R is closed, we have . This displays R as the adjoint of the globally defined, bounded operator R*. We then conclude that R is a globally defined, bounded operator as well.

Now by a “one-page” argument, we have shown that Ker   R* = 0, and so, Uμ,t is one-to-one. And by a “one-line” proof, we have seen that Ran  R* is dense, and so Uμ,t is onto. The two preceding assertions about Uμ,t follow from the polar decomposition Theorem 2.3. We conclude that Uμ,t is a unitary isomorphism.

We now write (3.26) equivalently as

(3.27)
for all ψ ∈ L2(ωμ,t) and all z ∈ ℂN. Now we apply Rμ,t to both sides, recalling that there is an implicit analytic continuation on the left side which cancels with Rμ,t, to get
(3.28)
for all x ∈ ℝN and all ψ ∈ L2(ωμ,t). So, we have the operator equation
(3.29)
where each side is a bounded operator from L2(ωμ,t) to itself. Also all of the operators in this equation are bounded. This then implies that
(3.30)
on . Of course, is not a bounded operator. However, its domain is dense in L2(ωμ,t). (Proof: using the Dunkl transform ℱμ,t (see [16–19]), one shows that the bounded operator is unitarily equivalent to multiplication by acting on L2(ℝN, ωμ,t), where k is the variable in ℝN. But the range of multiplication by clearly contains and so is dense by a standard argument in analysis.) Moreover, we also have
(3.31)
on as one sees by applying both sides to an arbitrary element , where ψ ∈ L2(ωμ,t), and by using the semigroup property. This in turn gives us
(3.32)
on the dense domain . Since both and Rμ,tUμ,t are globally defined, bounded operators that are equal on a dense domain, it follows that
(3.33)
on L2(ωμ,t). So for all x ∈ ℝN and all ψ ∈ L2(ωμ,t), we obtain
(3.34)
Next, we write out the left side as follows:
(3.35)
So for all x ∈ ℝN and all ψ ∈ L2(ωμ,t), we find that
(3.36)
and so Rμ,tUμ,t = Rμ,tCμ,t. Using that Rμ,t is injective (i.e., uniqueness of analytic continuation), we finally arrive at the desired identity, Uμ,t = Cμ,t, and therefore, Cμ,t is a unitary isomorphism as we wanted to prove.

During the proof of the previous theorem we proved the statement made earlier that Rμ,t is bounded. We now state this result separately and amplify on it.

Theorem 3.7. The operator R ≡ Rμ,t is bounded and has operator norm ∥R∥ = 1. Also the operator R* is bounded with operator norm ∥R*∥ = 1.

Proof. In this proof we denote all operator norms by ∥·∥. We already have shown that is a self-adjoint, bounded operator acting on L2(ℝN, ωμ,t) and that R and R* are globally defined, bounded operators. We take ϕ ∈ L2(ℝN, ωμ,t) in the following, getting

(3.37)
We also compute directly
(3.38)
since Spec(Δμ) = (−∞, 0] and t > 0. The result now follows.

4. Versions A, B, and D

Now we will apply the method indicated after the statement of the polar decomposition Theorem 2.3 in order to show that the A-version of the Segal-Bargmann transform can be obtained by a polar decomposition which is related to the polar decomposition (namely, the restriction principle) used to obtain the C-version. So, we are looking for two unitary isomorphisms, F1 and F2, making the following diagram commute:

image

(4.1)
Then we can use these two unitaries to change the polar decomposition which gave us Cμ,t into a polar decomposition giving Aμ,t. Of course, the very existence of such a pair, F1 and F2, already would prove that Aμ,t is a unitary isomorphism.
We use a known relation between the A and C-versions in order to start. The rest of the construction then follows in a systematic, algorithmic manner. The relation between these two versions that we use starts from this identity for the integral kernels
(4.2)
for all z ∈ ℂN and all q ∈ ℝN. (See [6, Theorem 3.5]). Now we translate this relation into a relation between the integral transforms themselves. From the defining equation (2.5) we have the scaling relation for λ > 0. By taking λ = 21/2 and replacing t with t/2 in this, we have
(4.3)
Next we replace z with 2−1/2z to obtain
(4.4)
To understand the integral kernel Aμ,t(z, 21/2q), we take ψ ∈ L2(ℝN, ωμ,t) and evaluate as follows:
(4.5)
where we used , the scaling property , and the definition of the dilation operator . Next, by multiplying both sides of (4.4) by ψ ∈ L2(ℝN, ωμ,t) and then integrating with respect to dωμ,t(q), we get
(4.6)
A crucial point here is that the factor does not depend on the variable of integration and so factors out in front of of the integral. Equivalently,
(4.7)
which itself is equivalent to the operator equation
(4.8)
where denotes the operator of multiplication by the function . Now we solve the last equation for Aμ,t getting
(4.9)
Next, we want the operator Cμ,t to be sandwiched between two unitary operators, and so it is not initially clear how to divide up the factors of 2 in (4.9) to get multiples of and of that are unitaries. But by Lemma 2.1 we know that
(4.10)
is a unitary isomorphism. The desired domain and the desired codomain of this unitary operator are determined by diagram (4.1). So it remains to show what is happening with the operator . According to the diagram (4.1) this should be the unitary isomorphism F2 : 𝒞μ,t → ℬμ,t indicated there.

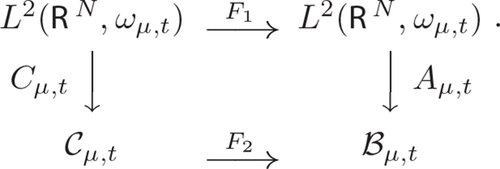
Therefore we would like to take f ∈ 𝒞μ,t and calculate the norms and and then show they are equal. But we do not have closed formulas for these norms for general elements in these reproducing kernel Hilbert spaces. However, it suffices to consider the case when f = Lz ∈ 𝒞μ,t, where z ∈ ℂN is arbitrary. See (3.4). In spite of the quantity of details, this does work out in an algorithmic manner.

Nevertheless, purely for the sake of simplicity, we prefer to give a shorter proof by relating F2 with known entities. We note first that G : 𝒞μ,t → ℬμ,t/2 is a unitary isomorphism. (See (3.6) and the subsequent discussion.) And second from a result in [6] we have that is also a unitary isomorphism. So the composition is again a unitary isomorphism. For any f ∈ 𝒞μ,t we use (3.6) to calculate this composition, giving for all w ∈ ℂN that
(4.11)
which in turn implies the operator equation
(4.12)
It follows that F2 : 𝒞μ,t → ℬμ,t is a unitary isomorphism.
We are now ready to apply the method discussed in the remarks just after the polar decomposition Theorem 2.3. Using the notation established there, we let
(4.13)
be defined as
(4.14)
Also, we already defined . So we have shown above that F1 and F2 are unitary isomorphisms and that diagram (4.1) commutes.
Of course, we have from (4.9) and the subsequent results that is a unitary isomorphism, since it is the composition of three unitary isomorphisms. We now want to see how Aμ,t arises explicitly from the corresponding polar decomposition (which, according to our definition, will turn out not to be a restriction principle) and how this polar decomposition relates to the unmotivated definition of a “restriction” operator in [12]. So, continuing with the notation established earlier, we have that Aμ,t arises in the polar decomposition B = V|B|; that is, V = Aμ,t, where . (Recall that we have shown that Rμ,t and are globally defined, bounded operators.) It follows that , and therefore, Aμ,t arises from the restriction principle according to our definition exactly when is the restriction operator ℬμ,t → L2(ℝN, ωμ,t); namely, . We know that and so . But from (3.6), we immediately have
(4.15)
So for f ∈ ℬμ,t we have for w ∈ ℂN that
(4.16)
Then since Rμ,t is simply restriction, we obtain for all x ∈ ℝN that
(4.17)
Finally, applying yields for all f ∈ ℬμ,t and  x ∈ ℝN
(4.18)
which is not the restriction operator. Consequently, this polar decomposition is not a restriction principle. However, notice that the operator is globally defined and bounded, since Rμ,t is globally defined and bounded. This fact is not so obvious by merely inspecting the right side of (4.18).
The operator in (4.18) does not compare very well at first sight with the “restriction operator” defined in [12, page 298]. But this discrepancy is easily understood. In [6, Corollary 3.1] we give the unitary equivalence between Aμ,1 and the “generalized Segal-Bargmann transform” BSO defined in [12]. (N.B. only the case t = 1 is considered in [12].) Using this we can conjugate the polar decomposition used above in order to obtain Aμ,1 to get an operator, say S, whose polar decomposition gives us BSO. We note that S is globally defined and bounded, since it is unitarily equivalent to . The adjoint of S (which should be the restriction operator) for all f ∈ ℬμ,t and x ∈ ℝN turns out to be
(4.19)
which is not a restriction operator according to our definition. Except for the positive multiplicative constant , this agrees with the “restriction operator” given in [12]. But for any closed, densely defined operator T and any λ > 0, the polar decompositions of T and λT give the same partial isometry. And this explains how the unmotivated “restriction operator” used in [12] arises in a natural manner in our presentation.

We wish to note that formula (4.18) was forced on us by our method, once we had established that the unitary operators F1 and F2 change the transform Cμ,t into Aμ,t. (cp. diagram (4.1).) And these two unitaries arose in a natural, motivated way directly from an identity that relates the kernel functions of these transforms. So the A-version arises by applying polar decomposition to a particular operator. When one thinks of it this way, this is a rather unimpressive result. Actually, every unitary operator between two Hilbert spaces can be realized via a polar decomposition. And any closed, densely defined operator which satisfies two additional hypotheses (injectivity and dense range) gives us a unitary operator in its polar decomposition.

Moreover, we could have used another pair of unitary isomorphisms, say G1 and G2 in place of F1 and F2, to change Cμ,t into , using a diagram analogous to (4.1). Then Z arises from the polar decomposition that comes from the restriction principle used to produce Cμ,t. However, this polar decomposition in general will not be a restriction principle. (e.g., the codomains of G1 and G2 need not even be function spaces.) Actually, any unitary isomorphism Z between separable, complex Hilbert spaces of infinite dimension can arise this way by an appropriate, but far from unique, choice of the two unitaries G1 and G2. So in general it would be misleading to dub Z with a name that indicates that it forms a part of Segal-Bargmann analysis.

However, the transform Aμ,t does arise naturally and uniquely from the heat kernel method as a part of Segal-Bargmann analysis. (See [6].) So it is reasonable to ask (and answer, as we have done in this section) how the restriction principle for Cμ,t gives us a polar decomposition of Aμ,t. On the other hand, we have not been able to find in [12] a satisfactory, explicit justification for considering the transform defined there as a part of Segal-Bargmann analysis. For example, Remark 4.3 ([12, page 301]) only indicates what happens when μ ≡ 0 (in our notation). In our opinion this is very far from justifying the terminology “Segal-Bargmann” for the case of general μ.

One point of this section is to show where the unmotivated exponential factor comes from in the definition of the “restriction operator” in [12]. It is truly a deus ex machina in [12]. Here it flows out naturally from an analysis based on the C-version. The second point of this section is to provide contrast with the method used to define the C-version in the last section. While that was also a polar decomposition, it was a particular, uniquely defined special case, namely the restriction principle. The worst that could happen with an analysis based on the restriction principle is that the technical details do not work out and therefore no unitary isomorphism at all is produced. In short, the result of the method is unique but may not exist.

As for the remaining two versions of the Segal-Bargmann, the Version B (resp., D) is defined by a unitary transformation (a change of measure) on the domain space starting with the Version A (resp., C). (See [6] for details about Version B. Version D is related to Version C analogously.) So, the restriction principle for the C-version implies that these remaining two versions can also be obtained from the polar decomposition of an explicitly defined operator. The details are left to the interested reader. We do wish to comment that these polar decompositions are not restriction principles. The brevity of our discussion in this paragraph is not meant to indicate that these versions are less important than the A-version. On the contrary, we think that the three versions A, B, and D have the same relative relation to the truly important and logically central C-version.

5. Concluding Remarks

Our confusion over the role in [12] of their “restriction principle” in the Segal-Bargmann analysis motivated our study of this topic. The upshot is our discovery of the central role of the restriction principle in the C-version of the Segal-Bargmann analysis associated to a finite Coxeter group. We wish to underscore that only the A-version of the Segal-Bargmann analysis is considered in [12]. This can be clearly seen in the reproducing kernel for the space of holomorphic functions in [12], which is therefore the A-version space. Also the “generalized Segal-Bargmann transform” in [12] has an integral kernel which is not the analytically continued heat kernel (as in the C-version), but rather something that corresponds to our uniquely defined A-version (modulo normalization and dilation). There is no mention in [12] of the C-version nor even of the existence of other versions of the Segal-Bargmann analysis.

In summary, we think that this paper shows that the restriction principle and the C-version (and not any other version) of Segal-Bargmann analysis are naturally and closely related with each other. So this is a new way for understanding how the C-version in general is the most fundamental version of the Segal-Bargmann analysis.

As for future endeavors, we note that we have studied only the case μ ≥ 0 and so it might be interesting to understand what happens when we drop or weaken that condition.

Acknowledgments

The author thanks Greg Stavroudis for a most hospitable venue for connecting to the Internet as well as for his excellent coffee, both being critical elements for doing the research for this paper. Also he warmly thanks Jean-Pierre Gazeau for being his academic host at the Université Paris Diderot Paris 7 during the spring of 2011 when this paper was finished. This research is partially supported by CONACYT (Mexico) project 49187.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.