Positive Almost Periodic Solutions for a Time-Varying Fishing Model with Delay
Abstract
This paper is concerned with a time-varying fishing model with delay. By means of the continuation theorem of coincidence degree theory, we prove that it has at least one positive almost periodic solution.
1. Introduction
The model (1.3) has recently attracted the attention of many mathematicians and biologists; see the differential equations which are widely used in fisheries [1, 2]. However, one can easily see that all equations considered in the above-mentioned papers are subject to periodic assumptions, and the authors, in particular, studied the existence of their periodic solutions. On the other hand, ecosystem effects and environmental variability are very important factors and mathematical models cannot ignore, for example, reproduction rates, resource regeneration, habitat destruction and exploitation, the expanding food surplus, and other factors that affect the population growth. Therefore it is reasonable to consider the various parameters of models to be changing almost periodically rather than periodically with a common period. Thus, the investigation of almost periodic behavior is considered to be more accordant with reality. Although it has widespread applications in real life, the generalization to the notion of almost periodicity is not as developed as that of periodic solutions; we refer the reader to [7–18].
Recently, the authors of [19] proved the persistence and almost periodic solutions for a discrete fishing model with feedback control. In [20, 21], the contraction mapping principle and the continuation theorem of coincidence degree have been employed to prove the existence of positive almost periodic exponential stable solutions for logarithmic population model, respectively. A primary purpose of this paper, nevertheless, is to utilize the continuation theorem of coincidence degree for this purpose. To the best of the authors’ observation, there exists no paper dealing with the proof of the existence of positive almost periodic solutions for (1.3) using the continuation theorem of coincidence degree. Therefore, our result is completely different and presents a new approach.
2. Preliminaries
- (A1)
a(t), b(t) ∈ C([0, +∞), [0, +∞)) and K(t) ∈ C([0, +∞), (0, +∞));
- (A2)
θ(t) is a continuous function on [0, +∞) that satisfies θ(t) ≤ t;
- (A3)
ϕ(t):(−∞, 0)→[0, ∞) is a continuous bounded function, ϕ(t) ≥ 0, y0 > 0.
By a solution of (2.1) and (2.2) we mean an absolutely continuous function y(t) defined on (−∞, +∞) satisfying (2.1) almost everywhere for t ≥ 0 and (2.2). As we are interested in solutions of biological significance, we restrict our attention to positive ones.
According to [22], the initial value problem (2.1) and (2.2) has a unique solution defined on (−∞, ∞).
Let X, Y be normed vector spaces, L : Dom L ⊂ X → Y be a linear mapping, and N : X → Y be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if dim Ker L = codim Im L < +∞ and Im L is closed in Y. If L is a Fredholm mapping of index zero and there exist continuous projectors P : X → X and Q : Y → Y such that Im P = Ker L, Ker Q = Im L = Im (I − Q), it follows that the mapping L|Dom L∩Ker P : (I − P)X → Im L is invertible. We denote the inverse of that mapping by KP. If Ω is an open bounded subset of X, then the mapping N will be called L-compact on , if is bounded and is compact. Since Im Q is isomorphic to Ker L, there exists an isomorphism J : Im Q → Ker L.
Theorem 2.1 (see [19].)Let Ω ⊂ X be an open bounded set and let N : X → Y be a continuous operator which is L-compact on . Assume that
- (1)
Ly ≠ λNy for every y ∈ ∂Ω∩Dom L and λ ∈ (0,1);
- (2)
QNy ≠ 0 for every y ∈ ∂Ω∩Ker L;
- (3)
the Brouwer degree deg {JQN, Ω∩Ker L, 0} ≠ 0.
3. Existence of Almost Periodic Solutions
Definition 3.1. y(t) ∈ C(ℝ, ℝ) is said to be almost periodic on ℝ if for any ɛ > 0 the set K(y, ɛ) = {δ:|y(t + δ) − y(t)| < ɛ, ∀t ∈ ℝ} is relatively dense; that is, for any ɛ > 0 it is possible to find a real number l(ɛ) > 0 for any interval with length l(ɛ); there exists a number δ = δ(ɛ) in this interval such that |y(t + δ) − y(t)| < ɛ for any t ∈ ℝ.
- (H)
a(t), b(t), K(t), t − θ(t) ∈ AP(ℝ), m(b/Kγ) ≠ 0 and m(a) ≠ m(b).
Remark 3.2. If f is ɛ-almost periodic function, then is ɛ-almost periodic if and only if m(f) = 0. Whereas f ∈ AP(ℝ) does not necessarily have an almost periodic primitive, m(f) = 0. That is why we can not make V1 = {z ∈ AP(ℝ) : m(z) = 0} and let V1 = {y ∈ AP(ℝ) : mod (y) ⊂ mod (F), ∀μ ∈ Λ(y) satisfy | μ | > α}.
We start with the following lemmas.
Lemma 3.3. X and Y are Banach spaces endowed with the norm ∥·∥.
Proof. If yn ∈ V1 and yn converge to y0, then it is easy to show that y0 ∈ AP(ℝ) with mod (y0) ⊂ mod (F). Indeed, for all we have
Lemma 3.4. Let L : X → Y and
Proof. It is obvious that L is a linear operator and Ker L = V2. It remains to prove that Im L = V1. Suppose that ϕ(t) ∈ Im L ⊂ Y. Then, there exist ϕ1 ∈ V1 and ϕ2 ∈ V2 such that
Lemma 3.5. Let N : X → Y, P : X → X, and Q : Y → Y such that
Proof. The projections P and Q are continuous such that
The integral form of the terms of both QN and (I − Q)N implies that they are continuous. We claim that KP is also continuous. By our hypothesis, for any ɛ < 1 and any compact set S ⊂ C((−∞, 0], ℝ), let l(ɛ, S) be the inclusion interval of K(F, ɛ, S). Suppose that {zn(t)} ⊂ Im L = V1 and zn(t) uniformly converges to z0(t). Because , there exists ρ(0 < ρ < ɛ) such that . Let l(ρ, S) be the inclusion interval of K(F, ρ, S) and
From (3.26), we also have that and KP(I − Q)Ny are uniformly bounded in . In addition, it is not difficult to verify that is bounded and KP(I − Q)Ny is equicontinuous in . Hence by the Arzelà-Ascoli theorem, we can immediately conclude that is compact. Thus N is L-compact on .
Theorem 3.6. Let condition (H) hold. Then (2.1) has at least one positive almost periodic solution.
Proof. It is easy to see that if (2.1) has one almost periodic solution , then is a positive almost periodic solution of (1.3). Therefore, to complete the proof it suffices to show that (2.1) has one almost periodic solution.
In order to use the continuation theorem of coincidence degree theory, we set the Banach spaces X and Y the same as those in Lemma 3.3 and the mappings L, N, P, Q the same as those defined in Lemmas 3.4 and 3.5, respectively. Thus, we can obtain that L is a Fredholm mapping of index zero and N is a continuous operator which is L-compact on . It remains to search for an appropriate open and bounded subset Ω. Corresponding to the operator equation
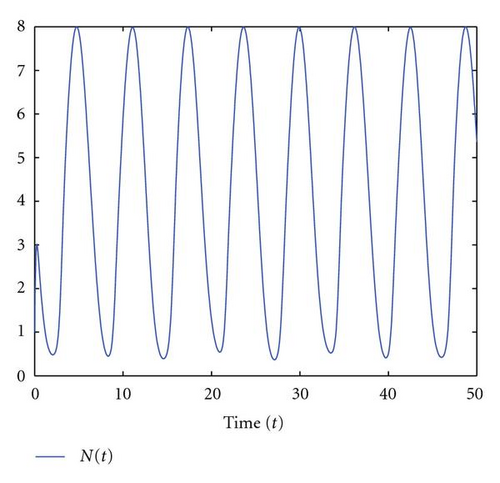
4. An Example
Acknowledgment
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 10971183.




