International Journal of Mathematics and Mathematical Sciences
Volume 2011, Issue 1 324821
Research Article
Open Access

Restricted Algebras on Inverse Semigroups—Part II: Positive Definite Functions

Massoud Amini, 

Corresponding Author

Massoud Amini

Department of Mathematics, Faculty of Mathematical Sciences, Tarbiat Modares University, P.O.Box Tehran 14115-134, Iran modares.ac.ir

Search for more papers by this author
Alireza Medghalchi, 

Alireza Medghalchi

Faculty of Mathematical Sciences and Computer, Tarbiat Moalem University, 50 Taleghani Avenue, Tehran 15614, Iran modares.ac.ir

Search for more papers by this author
First published: 05 September 2011
https://doi.org/10.1155/2011/324821
Citations: 2
Academic Editor: Naseer Shahzad

Abstract

The relation between representations and positive definite functions is a key concept in harmonic analysis on topological groups. Recently this relation has been studied on topological groupoids. In this paper, we investigate the concept of restricted positive definite functions and their relation with restricted representations of an inverse semigroup. We also introduce the restricted Fourier and Fourier-Stieltjes algebras of an inverse semigroup and study their relation with the corresponding algebras on the associated groupoid.

1. Introduction

In [1] we introduced the concept of restricted representations for an inverse semigroup S and studied the restricted forms of some important Banach algebras on S. In this paper we continue our study by considering the relation between the restricted positive definite functions and restricted representations. In particular, in Section 2 we prove restricted version of the Godement′s characterization of positive definite functions on groups (Theorem 2.9). In Section 3 we study the restricted forms of the Fourier and Fourier-Stieltjes algebras on S. The last section is devoted to the study of the Fourier and Fourier-Stieltjes algebras on the associated groupoid of S, as well as the C*-algebra of certain related graph groupoids.

An inverse semigroup S is a discrete semigroup such that for each s ∈ S there is a unique element s* ∈ S such that
(1.1)
The set E of idempotents of S consists of elements of the form ss*,   s ∈ S. Then E is a commutative subsemigroup of S. There is a natural order ≤ on E defined by e ≤ f if and only if ef = e. A *- representation of S is a pair {π, ℋπ} consisting of a (possibly infinite dimensional) Hilbert space ℋπ and a map π : S → ℬ(ℋπ) satisfying
(1.2)
that is, a *-semigroup homomorphism from S into the *-semigroup of partial isometries on ℋπ. Let Σ = Σ(S) be the family of all *-representations π of S with
(1.3)
For 1 ≤ p < ∞, ℓp(S) is the Banach space of all complex valued functions f on S satisfying
(1.4)
For p = ∞, ℓ∞(S) consists of those f with ∥f∥∞ : = sup x∈S|f(x)| < ∞. Recall that ℓ1(S) is a Banach algebra with respect to the product
(1.5)
and ℓ2(S) is a Hilbert space with inner product
(1.6)
Let also put
(1.7)
for each f ∈ ℓp(S)  (1 ≤ p ≤ ∞).
Given x, y ∈ S, the restricted product of x, y is xy if x*x = yy* and undefined, otherwise. The set S with its restricted product forms a groupoid Sa, called the associated groupoid of S [2]. If we adjoin a zero element 0 to this groupoid and put 0* = 0, we get an inverse semigroup Sr with the multiplication rule
(1.8)
which is called the restricted semigroup of S. A restricted representation {π, ℋπ} of S is a map π : S → ℬ(ℋπ) such that π(x*) = π(x)*(x ∈ S) and
(1.9)
Let Σr = Σr(S) be the family of all restricted representations π of S with ∥π∥ = sup x∈S∥π(x)∥ ≤ 1. It is not hard to guess that Σr(S) should be related to Σ(Sr). Let Σ0(Sr) be the set of all π ∈ Σ(Sr) with π(0) = 0. Note that Σ0(Sr) contains all cyclic representations of Sr. Now it is clear that, via a canonical identification, Σr(S) = Σ0(Sr). Two basic examples of restricted representations are the restricted left and right regular representations λr and ρr of S [1]. For each ξ, η ∈ ℓ1(S) put
(1.10)
then (ℓ1(S), ·,   ~) is a semisimple Banach *-algebra [1] which is denoted by and is called the restricted semigroup algebra of S.
All over this paper, S denotes a unital inverse semigroup with identity 1. E denotes the set of idempotents of S which consists of elements of the form ss*,   s ∈ S. Σ = Σ(S) is the family of all *-representations π of S with
(1.11)

2. Restricted Positive Definite Functions

A bounded complex valued function u : S → ℂ is called positive definite if for all positive integers n and all c1, …, cn ∈ ℂ, and x1, …, xn ∈ S, we have
(2.1)
and it is called restricted positive definite if for all positive integers n and all c1, …, cn ∈ ℂ, and x1, …, xn ∈ S, we have
(2.2)
We denote the set of all positive definite and restricted positive definite functions on S by P(S) and Pr(S), respectively. The two concepts coincide for (discrete) groups.
It is natural to expect a relation between Pr(S) and P(Sr). Before checking this, note that Sr is hardly ever unital. This is important, as the positive definite functions in nonunital case should be treated with extra care [3]. Let us take any inverse semigroup T with possibly no unit. Of course, one can always adjoin a unit 1 to T with 1* = 1 to get a unital inverse semigroup T1 = T ∪ {1} (if T happened to have a unit we put T1 = T). However, positive definite functions on T do not necessarily extend to positive definite functions on T1. Following [3], we consider the subset Pe(T) of extendible positive definite functions on T which are those u ∈ P(T) such that , and there exists a constant c > 0 such that for all n ≥ 1, x1, …, xn ∈ T, and c1, …, cn ∈ ℂ,
(2.3)
If τ : ℓ∞(T) → ℓ1(T)* is the canonical isomorphism, then τ maps Pe(T) onto the set of extendible positive bounded linear functionals on ℓ1(T) (those which are extendible to a positive bounded linear functional on ℓ1(T1)), and the restriction of τ to Pe(T) is an isometric affine isomorphism of convex cones [3, 1.1]. Also the linear span Be(T) of Pe(T) is an algebra [3, 3.4] which coincides with the set of coefficient functions of *-representations of T [3, 3.2]. If T has a zero element, then so is T1. In this case, we put P0(T) = {u ∈ P(T) : u(0) = 0} and P0,e(T) = P0(T)∩Pe(T). To each u ∈ Pe(T), there corresponds a cyclic *- representation of ℓ1(T1) which restricts to a cyclic representation of T (see the proof of [3, 3.2]). Let ω be the direct sum of all cyclic representations of T obtained in this way, then the set of all coefficient functions of ω is the linear span of Pe(T) [3, 3.2]. We call ω the universal representation of T.

All these arrangements are for T = Sr, as it is an inverse 0-semigroup which is not unital unless S is a group. We remind the reader that our blanket assumption is that S is a unital inverse semigroup. From now on, we also assume that S has no zero element (see Example 2.2).

Lemma 2.1. The restriction map τ : P0(Sr) → Pr(S) is an affine isomorphism of convex cones.

Proof. Let u ∈ P(Sr). For each n ≥ 1, x1, …, xn ∈ Sr and c1, …, cn ∈ ℂ, we have

(2.4)
in particular if u ∈ P0(Sr), then
(2.5)
so τ maps P0(Sr) into Pr(S).

τ is clearly an injective affine map. Also if u ∈ Pr(S) and v is extension by zero of u on Sr, then from the above calculation applied to v, v ∈ P0(Sr) and τ(v) = u, so τ is surjective.

It is important to note that the restriction map τ may fail to be surjective when S already has a zero element.

Example 2.2. If S = [0,1] with discrete topology and operations

(2.6)
then S is a zero inverse semigroup with identity. Here Sr = S, as sets, P(S) = {u   : u ≥ 0, u  is  decreasing} [4], but the constant function u = 1 is in Pr(S). This in particular shows that the map τ is not necessarily surjective, if S happens to have a zero element. To show that 1 ∈ Pr(S) note that for each n ≥ 1, each c1, …, cn ∈ ℂ and each x1, …xn ∈ S, if y1, …, yk are distinct elements in {x1, …, xn}, then for Jl : = {j   : 1 ≤ j ≤ n, xj = yl}, we have Ji = Jl, whenever i ∈ Jl, for each 1 ≤ i, l ≤ k. Hence
(2.7)

Notation 1. Let P0,e(Sr) be the set of all extendible elements of P0(Sr). This is a subcone which is mapped isomorphically onto a subcone Pr,e(S) by τ. The elements of Pr,e(S) are called extendible restricted positive definite functions on S. These are exactly those u ∈ Pr(S) such that , and there exists a constant c > 0 such that for all n ≥ 1, x1, …, xn ∈ S and c1, …, cn ∈ ℂ,

(2.8)

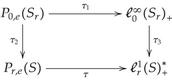
Proposition 2.3. There is an affine isomorphism τ of convex cones from Pr,e(S) onto

(2.9)

Proof. The affine isomorphism is just the restriction of the linear isomorphism of [1, Theorem  4.1] to the corresponding positive cones. Let us denote this by τ3. In Notation 1 we presented an affine isomorphism τ2 from Pe,e(Sr) onto Pr,e(S). Finally [3, 1.1], applied to Sr, gives an affine isomorphism from Pe(Sr) onto , whose restriction is an affine isomorphism τ1 from P0,e(Sr) onto . Now the obvious map τ, which makes the diagram

image

(2.10)
commutative, is the desired affine isomorphism.

In [5] the authors defined the Fourier algebra of a topological foundation *-semigroups (which include all inverse semigroups) and in particular studied positive definite functions on these semigroups. Our aim in this section is to develop a parallel theory for the restricted case and among other results prove the generalization of the Godement′s characterization of positive definite functions on groups [6] in our restricted context (Theorem 2.9).

For F, G⊆S, put
(2.11)
This is clearly a finite set, when F and G are finite.

Lemma 2.4. If S is an inverse semigroup and f, g ∈ ℓ2(S), then . In particular, when f and g are of finite supports, then so is .

Proof. if and only if xy ∈ supp (f), for some y ∈ supp (g) with x*x = yy*. This is clearly the case if and only if x = st*, for some s ∈ supp (f) and t ∈ supp (g) with s*s = t*t. Hence .

The following lemma follows from the fact that the product f · g is linear in each variable.

Lemma 2.5 (polarization identity). For each  f, g ∈ ℓ2(S)

(2.12)
where .

Lemma 2.6. For each φ ∈ Pr,f(S), one has .

Proof. For each  x, y ∈ S

(2.13)
Now if xx* = yy* then for z = y*x we have zz* = y*xx*y = y*y, and conversely zz* = y*y and x = yz imply that z = zz*z = y*yz = y*x, and then x = yy*x and xz* = y, so y = xz* = xx*y, that is, yy* = xx*yy* = yy*xx* = xx*. Hence the last sum is φ(y*x) if xx* = yy*, and it is zero, otherwise. Summing up,
(2.14)
Now for , we get
(2.15)

Lemma 2.7. With the above notation,

(2.16)
for each f, g ∈ ℓ1(S).

Proof. Given f, g ∈ ℓ1(S) and ξ ∈ ℓ2(S), put and , then η, ζ ∈ ℓ2(S) and, for each x ∈ S,

(2.17)
which are obviously the same.

Lemma 2.8. For each π ∈ Σr(S) and each ξ ∈ ℋπ, the coefficient function u = 〈π(·)ξ, ξ〉 is in Pr,e(S).

Proof. For each n ≥ 1, c1, …, cn ∈ ℂ and x1, …, xn ∈ S, noting that π is a restricted representation,we have

(2.18)
and, regarding π as an element of Σ0(Sr) and using the fact that u(0) = 0, we have
(2.19)
so u ∈ P0,e(Sr) = Pr,e(S).

The following is proved by R. Godement in the group case [6]. Here we adapt the proof given in [7].

Theorem 2.9. Let S be a unital inverse semigroup. Given φ ∈ ℓ∞(S), the following statements are equivalent:

  • (i)

    φ ∈ Pr,e(S),

  • (ii)

    there is an ξ ∈ ℓ2(S) such that .

Moreover if ξ is of finite support, then so is φ.

Proof. By the above lemma applied to π = λr, (ii) implies (i). Also if , then by Lemma 2.4, is of finite support.

Conversely assume that φ ∈ Pr,e(S). Choose an approximate identity {eα} for consisting of positive, symmetric functions of finite support, as constructed in [1, Proposition  3.2]. Let ρr be the restricted right regular representation of S, then by the above lemma . Take , then if 1 ∈ S is the identity element, then for each α ≥ β we have

(2.20)
as α, β → ∞, where the last equality follows from [1, Lemma  3.2(ii)]. Hence, there is ξ ∈ ℓ2(S) such that ξα → ξ in ℓ2(S). Now for each  t ∈ S
(2.21)
The last equality follows from the remark after Proposition  3.2 in [1] and the fact that . Hence , as required.

3. Restricted Fourier and Fourier-Stieltjes Algebras

Let S be a unital inverse semigroup and, let P(S) be the set of all bounded positive definite functions on S (see [8] for the group case and [9] for inverse semigroups). We use the notation P(S) with indices r, e, f, and 0 to denote the positive definite functions which are restricted, extendible, of finite support, or vanishing at zero, respectively. Let B(S) be the linear span of P(S). Then B(S) is a commutative Banach algebra with respect to the pointwise multiplication and the following norm [5]:
(3.1)
Also B(S) coincides with the set of the coefficient functions of elements of Σ(S) [5]. If one wants to get a similar result for the set of coefficient functions of elements of Σr(S), one has to apply the above facts to Sr. But Sr is not unital in general, so one is led to consider a smaller class of bounded positive definite functions on Sr. The results of [3] suggests that these should be the class of extendible positive definite functions on S. Among these, those which vanish at 0 correspond to elements of Pr,e(S).

The structure of algebras B(S) and A(S) is far from being well understood, even in special cases. From the results of [4, 10], it is known that for a commutative unital discrete *-semigroup S, via Bochner theorem [10]. Even in this case, the structure of A(S) seems to be much more complicated than the group case. This is mainly because of the lack of an appropriate analog of the group algebra. If S is a discrete idempotent semigroup with identical involution. Then is a compact topological semigroup with pointwise multiplication. We believe that in this case where is the Baker algebra on (see e.g., [8]) however we are not able to prove it at this stage. In this section we show that the linear span Br,e(S) of Pr,e(S) is a commutative Banach algebra with respect to the pointwise multiplication and an appropriate modification of the above norm. We call this the restricted Fourier-Stieltjes algebra of S and show that it coincides with the set of all coefficient functions of elements of Σr(S).

As before, the indices e, 0, and f are used to distinguish extendible elements, elements vanishing at 0, and elements of finite support, respectively. We freely use any combination of these indices. Consider the linear span of Pr,e,f(S) which is clearly a two-sided ideal of Br,e(S), whose closure Ar,e(S) is called the restricted Fourier algebra of S. We show that it is a commutative Banach algebra under pointwise multiplication and norm of Br(S).

In order to study properties of Br,e(S), we are led by Proposition 2.3 to consider B0,e(Sr). More generally we calculate this algebra for any inverse 0-semigroup T. Let Be(T) be the linear span of Pe(T) with pointwise multiplication and the norm
(3.2)
and let B0,e(T) be the closed ideal of Be(T) consisting of elements vanishing at 0. First let us show that Be(T) is complete in this norm. The next lemma is quite well known and follows directly from the definition of the functional norm.

Lemma 3.1. If X is a Banach space, D⊆X is dense, and f ∈ X*, then

(3.3)

Lemma 3.2. If T is an inverse 0-semigroup (not necessarily unital), then we have the following isometric isomorphism of Banach spaces:

  • (i)

    Be(T)≃C*(T)*,

  • (ii)

    .

In particular Be(T) and B0,e(T) are Banach spaces.

Proof. (ii) clearly follows from (i). To prove (i), first recall that Pe(S) is affinely isomorphic to [3, 1.1] via

(3.4)
This defines an isometric isomorphism τ0 from Be(T) into ℓ1(T)* (with the dual norm). By the brevious lemma, one can lift τ0 to an isometric isomorphism τ from Be(T) into C*(T)*. We only need to check that τ is surjective. Take any v ∈ C*(T), and let w be the restriction of v to ℓ1(T). Since ∥f∥Σ(T) ≤ ∥f∥1, for each f ∈ ℓ1(T), The norm of w as a linear functional on ℓ1(T) is not bigger than the norm of v as a functional on C*(T). In particular, w ∈ ℓ1(T)* and so there is a u ∈ Be(T) with τ0(u) = w. Then τ(u) = v, as required.

We know that the restriction map τ : B0,e(Sr) → Br,e(S) is a surjective linear isomorphism. Also τ is clearly an algebra homomorphism (B0,e(Sr) is an algebra under pointwise multiplication [3, 3.4], and the surjectivity of τ implies that the same fact holds for Br,e(S)). Now we put the following norm on Br(S)

(3.5)
then using the fact that B0,e(Sr) is a Banach algebra (it is a closed subalgebra of B(Sr) which is a Banach algebra [5, Theorem  3.4]) we have the following.

Lemma 3.3. The restriction map τ : B0,e(Sr) → Br,e(S) is an isometric isomorphism of normed algebras. In particular, Br,e(S) is a commutative Banach algebra under pointwise multiplication and above norm.

Proof. The second assertion follows from the first and Lemma 2.4 applied to T = Sr. For the first assertion, we only need to check that τ is an isometry. But this follows directly from [1, Theorem  3.2] and the fact that Σr(S) = Σ0(Sr).

Corollary 3.4. Br,e(S) is the set of coefficient functions of elements of Σr(S).

Proof. Given u ∈ Pr,e(S), let v be the extension by zero of u to a function on Sr, then v ∈ P0,e(Sr), so there is a cyclic representation π ∈ Σ(Sr), say with cyclic vector ξ ∈ ℋπ, such that v = 〈π(·)ξ, ξ〉 (see the proof of [3, 3.2]). But

(3.6)
that is, π(0)ξ = 0. But ξ is the cyclic vector of π, which means that for each η ∈ ℋπ, there is a net of elements of the form , converging to η in the norm topology of ℋπ, and
(3.7)
so π(0)η = 0, and so π(0) = 0. This means that π ∈ Σ0(Sr) = Σr(S). Now a standard argument, based on the fact that Σr(S) = Σ0(Sr) is closed under direct sum, shows that each u ∈ Br,e(S) is a coefficient function of some element of Σr(S). The converse follows from Lemma 2.8.

Corollary 3.5. One has the isometric isomorphism of Banach spaces Br,e(S)≃Cr(S)*.

Proof. We have the following of isometric linear isomorphisms: first Br,e(S)≃B0,e(Sr) (Lemma 3.3), then (Lemma 3.2, applied to T = Sr), and finally [1, Theorem  4.1].

Next, as in [5], we give an alternative description of the norm of the Banach algebra Br,e(S). For this we need to know more about the universal representation of Sr. The universal representation ω of Sr is the direct sum of all cyclic representations corresponding to elements of Pe(Sr). To be more precise, this means that given any u ∈ Pe(Sr) we consider u as a positive linear functional on ℓ1(Sr), then by [7, 21.24], there is a cyclic representation of ℓ1(Sr), with πu ∈ Σ(Sr), such that
(3.8)
Therefore πu is a cyclic representation of Sr and u = 〈πu(·)ξu, ξu〉 on Sr. Now ω is the direct sum of all πu′s, where u ranges over Pe(Sr). There is an alternative construction in which one can take the direct sum of πu′s with u ranging over P0,e(Sr) to get a subrepresentation ω0 of ω. Clearly ω ∈ Σ(Sr) and ω0 ∈ Σ0(Sr). It follows from [3, 3.2] that the set of coefficient functions of ω and ω0 are Be(Sr) and B0,e(Sr) = Br,e(S), respectively. As far as the original semigroup S is concerned, we prefer to work with ω0, since it could be considered as an element of Σr(S). Now is a nondegenerate *- representation of which uniquely extends to a nondegenerate representation of the restricted full C*-algebra , which we still denote by . We gather some of the elementary facts about in the next lemma.

Lemma 3.6. With the above notation, we have the following.

  • (i)

    is the direct sum of all nondegenerate representations πu of associated with elements via the GNS, construction, namely, is the universal representation of . In particular, is faithfully represented in .

  • (ii)

    The von Numann algebras and the double commutant of in are isomorphic. They are generated by elements , with , as well as by elements ω0(x), with x ∈ S.

  • (iii)

    Each representation π of uniquely decomposes as π = π**∘ω0.

  • (iv)

    For each π ∈ Σr(S) and ξ, η ∈ ℋπ, let u = 〈π(·)ξ, η〉, then u ∈ Cr(S)* and

    (3.9)

Proof. Statement (i) follows by a standard argument. Statement (iii) and the first part of (ii) follow from (i), and the second part of (ii) follows from the fact that both sets of elements described in (ii) have clearly the same commutant in as the set of elements , with which generate . The first statement of (iv) follows from Lemma 2.8 and Corollary 3.5. As for the second statement, first note that for each , is the image of f under the canonical embedding of in . Therefore, by (iii),

(3.10)
Taking limit in we get the same relation for any , and then, using (ii), by taking limit in the ultraweak topology of , we get the desired relation.

Lemma 3.7. Let 1 be the identity of S, then for each u ∈ Pr,e(S) one has ∥u∥r = u(1).

Proof. As and u(1) = λr(1)u(1) ≥ 0, we have ∥u∥r ≥ |u(1)| = u(1). Conversely, by the proof of Corollary 3.4, there is π ∈ Σr(S) and ξ ∈ ℋπ such that u = 〈π(·)ξ, ξ〉. Hence u(1) = 〈π(1)ξ, ξ〉 = ∥ξ∥2 ≥ ∥u∥r.

Lemma 3.8. For each π ∈ Σr(S) and ξ, η ∈ ℋπ, consider u = 〈π(·)ξ, η〉 ∈ Br,e(S), then ∥u∥r ≤ ∥ξ∥ · ∥η∥. Conversely each u ∈ Br,e(S) is of this form and one may always choose ξ, η so that ∥u∥r = ∥ξ∥ · ∥η∥.

Proof. The first assertion follows directly from the definition of ∥u∥r (see the paragraph after Lemma 3.6). The first part of the second assertion is the content of Corollary 3.4. As for the second part, basically the proof goes as in [9]. Consider u as an element of and let u = v · |u| be the polar decomposition of u, with and , and the dot product is the module action of on . Again, by the proof of Corollary 3.4, there is a cyclic representation π ∈ Σr(S), say with cyclic vector η, such that |u| = 〈π(·)η, η〉. Put , then ∥ξ∥ ≤ ∥η∥ and, by Lemma 3.6(iv) applied to |u|,

(3.11)
and, by Corollary 3.5 and Lemma 3.7,
(3.12)

Note that the above lemma provides an alternative (direct) way of proving the second statement of Lemma 3.3 (just take any two elements u, v in Br,e(S) and represent them as coefficient functions of two representations such that the equality holds for the norms of both u and v, then use the tensor product of those representations to represent uv and apply the first part of the lemma to uv). Also it gives the alternative description of the norm on Br,e(S) as follows.

Corollary 3.9. For each u ∈ Br,e(S),

(3.13)

Corollary 3.10. For each u ∈ Br,e(S),

(3.14)

Proof. Just apply Kaplansky′s density theorem to the unit ball of .

Corollary 3.11. The unit ball of Br,e(S) is closed in the topology of pointwise convergence.

Proof. If u ∈ Br,e(S) with ∥u∥r ≤ 1, then for each n ≥ 1, each c1, …, cn ∈ ℂ and each x1, …, xn ∈ S,

(3.15)
If uα → u, pointwise on S with uα ∈ Br,e(S), ∥uα∥r ≤ 1, for each α, then all uα′s satisfy above inequality, and so does u. Hence, by above corollary, u ∈ Br,e(S) and ∥u∥r ≤ 1.

Lemma 3.12. For each f, g ∈ ℓ2(S), and if ∥·∥r is the norm of Br,e(S), .

Proof. The first assertion follows from polarization identity of Lemma 2.5 and the fact that for each h ∈ ℓ2(S), is a restricted extendible positive definite function (Theorem 2.9). Now if , then

(3.16)

The next theorem extends Eymard′s theorem [9, 3.4] to inverse semigroups.

Theorem 3.13. Consider the following sets:

(3.17)
Then E1⊆E2⊆E3⊆E4⊆E5⊆E6⊆Br,e(S), and the closures of all of these sets in Br,e(S) are equal to Ar,e(S).

Proof. The inclusion E1⊆E2 follows from Lemma 2.5, and the inclusions E2⊆E3 and E4⊆E5 follow from Theorem 2.9. The inclusions E3⊆E4 and E5⊆E6 are trivial. Now E1 is dense in E6 by Lemma 3.12, and the fact that is dense in ℓ2(S). Finally , by definition, and E3⊆E2⊆E1 by Theorem 2.9; hence , for each 1 ≤ i ≤ 6.

Lemma 3.14. Pr,e(S) separates the points of S.

Proof. We know that Sr has a faithful representation (namely the left regular representation Λ), so Pe(Sr) separates the points of Sr [3, 3.3]. Hence P0,e(Sr) = Pr,e(S) separates the points of Sr∖{0} = S.

Proposition 3.15. For each x ∈ S there is u ∈ Ar,e(S) with u(x) = 1. Also Ar,e(S) separates the points of S.

Proof. Given x ∈ S, let , then u(x) = 1. Also given y ≠ x and u as above, if u(y) ≠ 1, then u separates x and y. If u(y) = 1, then use above lemma to get some v ∈ Br,e(S) which separates x and y. Then u(x) = u(y) = 1, so (uv)(x) = v(x) ≠ v(y) = (uv)(y); that is, uv ∈ Ar,e(S) separates x and y.

Proposition 3.16. For each finite subset K⊆S, there is u ∈ Pr,e,f(S) such that u|K ≡ 1.

Proof. For F⊆S, let Fe = {x*x : x ∈ F} and note that F⊆F · Fe (since x = x(x*x), for each x ∈ F). Now given a finite set K⊆S, put F = K ∪ K* ∪ Ke; then since we have F = F*, and since and we have Fe⊆F. Hence K⊆F⊆F · F. Now F · F is a finite set, and if f = χF, then and u|K ≡ 1.

Corollary 3.17. Br,e,f(S) = 〈Pr,e,f(S)〉 and = Ar,e(S).

Proof. Clearly 〈Pr,e,f(S)〉⊆Br,e,f(S). Now if v ∈ Br,e,f(S), then , for some αi ∈ ℂ and vi ∈ Pr,e,f(S)(1 ≤ i ≤ 4). Let K = supp (v)⊆S and u ∈ Pr,e,f(S) be as in the above proposition, then u|K ≡ 1 so is in the linear span of Pr,e,f(S).

4. Fourier and Fourier-Stieltjes Algebras of Associated Groupoids

We observed in Section 1 that one can naturally associate a (discrete) groupoid Sa to any inverse semigroup S. The Fourier and Fourier-Stieltjes algebras of (topological and measured) groupoids are studied in [11–14]. It is natural to ask if the results of these papers, applied to the associated groupoid Sa of S, could give us some information about the associated algebras on S. In this section we explore the relation between S and its associated groupoid Sa and resolve some technical difficulties which could arise when one tries to relate the corresponding function algebras. We also investigate the possibility of assigning graph groupoids to S and find relations between the corresponding C*-algebras.

Let us recall some general terminology and facts about groupoids. There are two parallel approaches to the theory of groupoids, theory of measured groupoids, and theory of locally compact groupoids (compare [13] with [14]). Here we deal with discrete groupoids (like Sa), and so basically it doesn′t matter which approach we take, but the topological approach is more suitable here. Even if one wants to look at the topological approach, there are two different interpretations about what we mean by a “representation” (compare [12] with [13]). The basic difference is that whether we want representations to preserve multiplications everywhere or just almost everywhere (with respect to a Borel measure on the unit space of our groupoid which changes with each representation). Again the “everywhere approach” is more suitable for our setting. This approach, mainly taken by [11, 12], is the best fit for the representation theory of inverse semigroups (when one wants to compare representation theories of S and Sa). Even then, there are some basic differences which one needs to deal with them carefully.

We mainly follow the approach and terminology of [12]. As we only deal with discrete groupoids we drop the topological considerations of [12]. This would simplify our short introduction and facilitate our comparison. A (discrete) groupoid is a set G with a distinguished subset G2⊆G × G of pairs of multiplicable elements, a multiplication map:G2 → G;   (x, y) ↦ xy, and an inverse map :G → G;   x ↦ x−1, such that for each x, y, z ∈ G
  • (i)

    ,

  • (ii)

    if (x, y), (y, z) are in G2, then so are (xy, z), (x, yz), and (xy)z = x(yz),

  • (iii)

    (x−1, x) is in G2 and if (x, y) is in G2 then x−1(xy) = y,

  • (iv)

    if (y, x) is in G2, then (yx)x−1 = y.

For x ∈ G, s(x) = x−1x and r(x) = xx−1 are called the source and range of x, respectively. G0 = s(G) = r(G) is called the unit space of G. For each u, v ∈ G0 we put Gu = r−1(u), Gv = s−1(v), and . Note that for each u ∈ G0, is a (discrete) group, called the isotropy group at u. Any (discrete) groupoid G is endowed with left and right Haar systems {λu} and {λu}, where λu and λu are simply counting measures on Gu and Gu, respectively. Consider the algebra c00(G) of finitely supported functions on G. We usually make this into a normed algebra using the so-called I-norm
(4.1)
where the above supremums are denoted, respectively, by ∥f∥I,s and ∥f∥I,r. Note that in general c00(G) is not complete in this norm. We show the completion of c00(G) in ∥·∥I by ℓ1(G). There are also natural C*-norms in which one can complete c00(G) and get a C*-algebra. Two-well known groupoid C*-algebras obtained in this way are the full and reduced groupoid C*-algebras C*(G) and . Here we briefly discuss their construction and refer the reader to [14] for more details.
A Hilbert bundle ℋ = {ℋu} over G0 is just a field of Hilbert spaces indexed by G0. A representation of G is a pair {π, ℋπ} consisting of a map π and a Hilbert bundle over G0 such that, for each x, y ∈ G,
  • (i)

    is a surjective linear isometry,

  • (ii)

    π(x−1) = π(x)*,

  • (iii)

    if (x, y) is in G2, then π(xy) = π(x)π(y).

We usually just refer to π as the representation, and it is always understood that there is a Hilbert bundle involved. We denote the set of all representations of G by Σ(G). Note that here a representation corresponds to a (continuous) Hilbert bundle, where as in the usual approach to (locally compact or measured) categories representations are given by measurable Hilbert bundles (see [12] for more details).

A natural example of such a representation is the left regular representation L of G. The Hilbert bundle of this representation is L2(G) whose fiber at u ∈ G0 is L2(Gu, λu). In our case that G is discrete, this is simply ℓ2(Gu). Each f ∈ c00(G) could be regarded as a section of this bundle (which sends u ∈ G0 to the restriction of f to Gu). Also G acts on bounded sections ξ of L2(G) via
(4.2)
Let E2(G) be the set of sections of L2(G) vanishing at infinity. This is a Banach space under the supnorm and contains c00(G). Furthermore, it is a canonical c0(G0)-module via
(4.3)
Now E2(G), with the c0(G)-valued inner product
(4.4)
is a Hilbert C*-module. The action of c00(G) on itself by left convolution extends to a *-anti representation of c00(G) in E2(G), which is called the left regular representation of c00(G) [12, Proposition  10]. The map f ↦ Lf is a norm decreasing homomorphism from (c00(G), ∥·∥I,r) into ℬ(E2(G)). Also the former has a left bounded approximate identity {eα} consisting of positive functions such that tends to the identity operator in the strong operator topology of the later [12, Proposition  11]. The closure of the image of c00(G) under L is a C*-subalgebra of ℬ(E2(G)) which is called the reduced C*-algebra of G. We should warn the reader that ℬ(E2(G)) is merely a C*-algebra and, in contrast with the Hilbert space case, it is not a von Neumann algebra in general. The above construction simply means that we have used the representation L to introduce an auxiliary C*-norm on c00(G) and took the completion of c00(G) with respect to this norm. A similar construction using all nondegenerate *-representations of c00(G) in Hilbert C*-modules yields a C*-completion C*(G) of c00(G), called the full C*-algebra of G.
Next one can define positive definiteness in this context. Let π ∈ Σ(G), for bounded sections ξ, η of ℋπ, the function
(4.5)
on G (where the inner product is taken in the Hilbert space ) is called a coefficient function of π. A function φ ∈ ℓ∞(G) is called positive definite if for all u ∈ G0 and all f ∈ c00(G)
(4.6)
or, equivalently, for each n ≥ 1, u ∈ G0, x1, …xn ∈ Gu, and α1, …, αn ∈ ℂ
(4.7)
We denote the set of all positive definite functions on G by P(G). The linear span B(G) of P(G) is called the Fourier-Stieltjes algebra of G. It is equal to the set of all coefficient functions of elements of Σ(G) [12, Theorem  1]. It is a unital commutative Banach algebra [12, Theorem  2] under pointwise operations and the norm ∥φ∥ = inf ∥ξ∥∥η∥, where the infimum is taken over all representations φ = 〈π(·)ξ∘s(·), η∘r(·)〉. On the other hand each φ ∈ B(G) could be considered as a completely bounded linear operator on C*(G) via
(4.8)
such that ∥φ∥∞ ≤ ∥φ∥cb ≤ ∥φ∥ [12, Theorem  3]. The last two norms are equivalent on B(G) (they are equal in the group case, but it is not known if this is the case for groupoids). Following [12] we denote B(G) endowed with cb-norm with ℬ(G). This is known to be a Banach algebra (This is basically [13, Theorem  6.1] adapted to this framework [12, Theorem  3]).
There are four candidates for the Fourier algebra A(G). The first is the closure of the linear span of the coefficients of E2(G) in B(G) [14], the second is the closure of ℬ(G)∩c00(G) in ℬ(G) [12], the third is the closure of the of the subalgebra generated by the coefficients of E2(G) in B(G), and the last one is the completion of the normed space of the quotient of by the kernel of θ from into c0(G) induced by the bilinear map θ : c00(G) × c00(G) → c0(G) defined by
(4.9)

These four give rise to the same algebra in the group case. We refer the interested reader to [12] for a comparison of these approaches. Here we adapt the third definition. Then A(G) is a Banach subalgebra of B(G) and A(G)⊆c0(G).

Now we are ready to compare the function algebras on inverse semigroup S and its associated groupoid Sa. We would apply the above results to G = Sa. First let us look at the representation theory of these objects. As a set, Sr compared to Sa has an extra zero element. Moreover, the product of two nonzero elements of Sr is 0, exactly when it is undefined in Sa. Hence it is natural to expect that Σ(Sa) is related to Σ0(Sr) = Σr(S). The major difficulty to make sense of this relation is the fact that representations of Sa are defined through Hilbert bundles, where as restricted representations of S are defined in Hilbert spaces. But a careful interpretation shows that these are two sides of one coin.

Lemma 4.1. One has Σr(S) = Σ(Sa).

Proof. Let E be the set of idempotents of S. First let us show that each π ∈ Σr(S) could be regarded as an element of Σ(Sa). Indeed, for each x ∈ S, π(x) : ℋπ → ℋπ is a partial isometry, so if we put ℋu = π(u)ℋπ  (u ∈ E), then we could regard π(x) as an isomorphism from . Using the fact that the unit space of Sa is , it is easy now to check that π ∈ Σ(Sa). Conversely suppose that π ∈ Σ(Sa), then for each x ∈ Sa, π(x) : ℋs(x) → ℋr(x) is an isomorphism of Hilbert spaces. Let ℋπ be the direct sum of all Hilbert spaces ℋu, u ∈ E, and define π(x)(ξu) = (ηv), where

(4.10)
then we claim that
(4.11)
First let us assume that x*x = yy*, then π(xy)(ξu) = (θv), where θv = 0, except for v = xyy*x* = xx*, for which . On the other hand, π(y)(ξu) = (η − v), where ηv = 0, except for v = yy*, for which , and π(x)(ηv) = (ζw), with ζw = 0, except for w = xx*, for which . Hence π(xy)(ξu) = π(x)π(y)(ξu), for each (ξu) ∈ ℋπ. Next assume that x*x ≠ yy*, then the second part of the above calculation clearly shows that π(x)π(y)(ξu) = 0. This shows that π could be considered as an element of Σr(S). Finally it is clear that these two embeddings are inverse of each other.

Next, Sr = Sa ∪ {0} as sets, and for each bounded map φ : Sr → ℂ with φ(0) = 0, it immediately follows from the definition that φ ∈ P(Sa) if and only if φ ∈ P0(Sr). Hence by above lemma we have the following.

Theorem 4.2. The Banach spaces Br(S) = B0(Sr) and B(Sa) are isometrically isomorphic.

This combined with [12, Theorem  2] (applied to G = Sa) shows that Br(S) is indeed a Banach algebra under pointwise multiplication and the above linear isomorphism is also an isomorphism of Banach algebras. By [12, Theorem  1] now we conclude by the following.

Corollary 4.3. Br(S) is the set of coefficient functions of Σr(S).

There are several other canonical ways to associate a groupoid (besides Sa) to S. Two natural candidates are the universal groupoid [15] and the graph groupoid [16]. The latter is indirectly related to Sr as it used the idea of adding a zero element to S. There is a vast literature on graph C*-algebras for which we refer the interested reader to [17] and references therein.

To associate a graph groupoid to S it is more natural to start with a (countable) discrete semigroup S without involution and turn it into an inverse semigroup using the idea of [16, Section  3]. Let S be such a semigroup, and let S* = {x* : x ∈ S} be a copy of S. Let s(x) = xx* and r(x) = x*x be defined formally. Put E = {r(x) : x ∈ S} ∪ {s(x) : x ∈ S}. Add a zero element 0 which multiplies everything to 0. Let ℰ be a directed graph with set of vertices being E, the set of direct and inverse edges are S and S*, respectively. Let Sℰ be the graph semigroup of ℰ. The inverse 0-semigroup generated by S ∪ S* is defined as the inverse semigroup generated by S ∪ S* subject to 0* = 0, , (xy)* = y*x*, and x*y = 0 unless x = y, for x, y ∈ S.

Lemma 4.4. Sℰ is an inverse semigroup, and if is the inverse 0-semigroup generated by S ∪ S*, then .

Proof. The graph semigroup Sℰ is the semigroup generated by E ∪ S ∪ S* ∪ {0} subject to the following relations [16]:

  • (i)

    0 is a zero for Sℰ,

  • (ii)

    s(x)x = x = xr(x) and r(x)x* = x* = x*s(x), for all x ∈ S,

  • (iii)

    ab = 0 if a, b ∈ E ∪ S ∪ S* and r(a) ≠ s(b),

  • (iv)

    x*y = 0 if x, y ∈ S and x ≠ y,

where, in (iii), the source and range of elements in E and S* are defined naturally. Then Sℰ is an inverse semigroup [16, Propositions  3.1]. Clearly the satisfies all the above relations, and the identity map is a semigroup isomorphism from Sℰ onto .

Let T be the set of all pairs (α, β) of finite paths in ℰ with r(α) = r(β) together with a zero element z; then T is naturally an inverse semigroup and T = Sℰ [16, Propositions  3.2]. Consider those paths of the form (x, x) where x ∈ S and let Ef be the set of all those idempotents e for which there are finitely many x ∈ S with s(x) = e. Let I be the closed ideal of ℓ1(T) generated by δz and elements of the form δ(e,e) − ∑s(x)=eδ(x,x) for e ∈ Ef. Then is the universal C*-algebra of ℓ1(T)/I [16].

Theorem 4.5. Let C*(ℰ) be the graph C*-algebra of ℰ. Then C*(ℰ) is a quotient of .

Proof. By the above lemma and the fact that T = Sℰ, there is a isometric epimorphism . let J be the closure of ker (ϕ) in the C*-norm of . Then . Now the result follows from the fact that [16, Corollary  3.9].

A (locally finite) directed graph ℰ is cofinal if given vertex v and infinite path α, there is a finite path β with s(β) = v and r(β) = r(α). It has no sinks if there are no edges emanating from any vertex.

Theorem 4.6. When ℰ has no loops, then is approximately finite dimensional. If moreover ℰ is cofinal, then is simple.

Proof. If ℰ has no loops, we have I = ℂz, hence J = 0 and epimorphism ϕ in the proof of the above theorem is an algebra isomorphism. Hence . But since ℰ has no loops, C*(ℰ) is an AF-algebra [18, Theorem  2.4]. Now assume that ℰ is also cofinal, then ℰ has no sinks hence is simple by [18, Corollary  3.11].

It also follows from [18, Corollary  3.11] that if ℰ has no sinks and is cofinal, but it has a loop, then is purely infinite. However this case never happens for the directed graph ℰ constructed above, as it has no loops when xx* = e or x*x = e implies that x = e, and has no sink when xx* = e implies that x = e, for each x ∈ S and e ∈ E, but these two conditions are clearly equivalent, and both are equivalent to S = E. A concrete example is S = (ℕ, max ) with n = n*. Also a sufficient condition for ℰ to be cofinal is that S is finitely transitive; namely, for each e, f ∈ E there are finitely many xi ∈ S, 1 ≤ i ≤ n with s(x1) = e, r(xn) = f and r(xi) = s(xi+1), for 1 ≤ i ≤ n − 1. Let us say that S is N-transitive if we could always find such a finite path with n ≤ N. A concrete example of a 1-transitive semigroup is the Brandt semigroup B2 consisting of all pairs (i, j), i, j ∈ {0,1}, plus zero element, with (i, j)(k, l) = (i, l) if j = k, and zero otherwise.

Acknowledgment

This research was supported in part by MIM Grant no. p83-118.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.