Integer Solutions of Integral Inequalities and H-Invariant Jacobian Poisson Structures
Abstract
We study the Jacobian Poisson structures in any dimension invariant with respect to the discrete Heisenberg group. The classification problem is related to the discrete volume of suitable solids. Particular attention is given to dimension 3 whose simplest example is the Artin-Schelter-Tate Poisson tensors.
1. Introduction
This paper continues the authors′ program of studies of the Heisenberg invariance properties of polynomial Poisson algebras which were started in [1] and extended in [2, 3]. Formally speaking, we consider the polynomials in n variables ℂ[x0, x1, …, xn−1] over ℂ and the action of some subgroup Hn of GLn(ℂ) generated by the shifts operators xi → xi+1(mod ℤn) and by the operators x → ɛixi, where ɛn = 1. We are interested in the polynomial Poisson brackets on ℂ[x0, x1, …, xn−1] which are “stable” under this actions (we will give more precise definition below).
The most famous examples of the Heisenberg invariant polynomial Poisson structures are the Sklyanin-Odesskii-Feigin-Artin-Tate quadratic Poisson brackets known also as the elliptic Poisson structures. One can also think about these algebras like the “quasiclassical limits” of elliptic Sklyanin associative algebras. These is a class of Noetherian graded associative algebras which are Koszul, Cohen-Macaulay, and have the same Hilbert function as a polynomial ring with n variables. The above-mentioned Heisenberg group action provides the automorphisms of Sklyanin algebras which are compatible with the grading and defines an Hn-action on the elliptic quadratic Poisson structures on ℙn. The latter are identified with Poisson structures on some moduli spaces of the degree n and rank k + 1 vector bundles with parabolic structure (= the flag 0 ⊂ F ⊂ ℂk+1 on the elliptic curve ℰ). We will denote this elliptic Poisson algebras by qn;k(ℰ). The algebras qn;k(E) arise in the Feigin-Odesskii “deformational” approach and form a subclass of polynomial Poisson structures. A comprehensive review of elliptic algebras can be found in [4] to which we refer for all additional information. We will mention only that as we have proved in [3] all elliptic Poisson algebras (being in particular Heisenberg-invariant) are unimodular.
Another interesting class of polynomial Poisson structures consists of so-called Jacobian Poisson structures (JPS). These structures are a special case of Nambu-Poisson structures. Their rank is two, and the Jacobian Poisson bracket {P, Q} of two polynomials P and Q is given by the determinant of Jacobi matrix of functions (P, Q, P1, …, Pn−2). The polynomials Pi, 1 ≤ i ≤ n − 2 are Casimirs of the bracket and under some mild condition of independence are generators of the centrum for the Jacobian Poisson algebra structure on ℂ[x0, …, xn−1]. This type of Poisson algebras was intensively studied (due to their natural origin and relative simplicity) in a huge number of publications among which we should mention [1, 5–9].
The paper is organized as follows: in Section 2, we remind a definition of the Heisenberg group in the Schroedinger representation and describe its action on Poisson polynomial tensors and also the definition of JPS. In Section 3, we treat the above mentioned enumerative problem in dimension 3. The last section concerns the case of any dimension. Here, we discuss some possible approaches to the general enumerative question.
2. Preliminary Facts
Throughout of this paper, K is a field of characteristic zero. Let us start by remembering some elementary notions of the Poisson geometry.
2.1. Poisson Algebras and Poisson Manifold
Let ℛ be a commutative K-algebra. One says that ℛ is a Poisson algebra if ℛ is endowed with a Lie bracket, indicated with {·, ·}, which is also a biderivation. One can also say that ℛ is endowed with a Poisson structure, and therefore, the bracket {·, ·} is called the Poisson bracket. Elements of the center are called Casimirs: a ∈ ℛ is a Casimir if {a, b} = 0 for all b ∈ ℛ.
A Poisson manifold M (smooth, algebraic, etc.) is a manifold whose function algebra 𝒜 (C∞(M), regular, etc.) is endowed with a Poisson bracket.
The polynomials Qi, i = 1, …, n − 2 are Casimir functions for the brackets (2.5).
There exists a second generalization of the Sklyanin algebra that we will describe briefly in the next subsection (see, for details, [4]).
2.2. Elliptic Poisson Algebras qn(ℰ, η) and qn,k(ℰ, η)
(We report here this subsection from [2] for sake of self-consistency).
These algebras, defined by Feĭgin and Odesskiĭ, arise as quasiclassical limits of elliptic associative algebras Qn(ℰ, η) and Qn,k(ℰ, η) [12, 13].
Let Γ = ℤ + τℤ ⊂ ℂ be an integral lattice generated by 1 and τ ∈ ℂ, with Im τ > 0. Consider the elliptic curve ℰ = ℂ/Γ and a point η on this curve.
- (1)
the center of the algebra Qn,k(ℰ, η), for generic ℰ and η, is the algebra of polynomial of m = pgcd(n, k + 1) variables of degree n/m,
- (2)
Qn,k(ℰ, 0) = ℂ[x1, …, xn] is commutative,
- (3)
Qn,n−1(ℰ, η) = ℂ[x1, …, xn] is commutative for all η,
- (4)
, if kk′ ≡ 1 (mod n),
- (5)
the maps xi ↦ xi+1 et xi ↦ ɛixi, where ɛn = 1, define automorphisms of the algebra Qn,k(ℰ, η),
- (6)
the algebras Qn,k(ℰ, η) are deformations of polynomial algebras. The associated Poisson structure is denoted by qn,k(ℰ, η),
- (7)
among the algebras qn,k(ℰ, η), only q3(ℰ, η) (the Artin-Schelter-Tate algebra) and the Sklyanin algebra q4(ℰ, η) are Jacobian Poisson structures.
2.3. The Heisenberg Invariant Poisson Structures
2.3.1. The G-Invariant Poisson Structures
Let G be a group acting on a Poisson algebra ℛ.
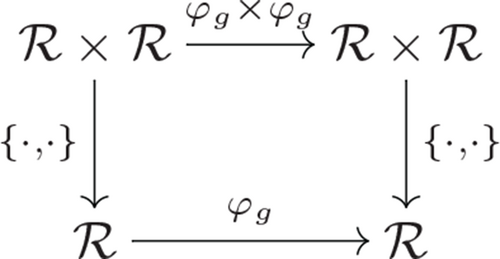
Definition 2.1. A Poisson bracket {·, ·} on ℛ is said to be a G-invariant if G acts on ℛ by Poisson automorphisms.
In other words, for every g ∈ G, the morphism φg : ℛ → ℛ, a ↦ g · a is an automorphism and the following diagram is a commutative:
2.3.2. The H-Invariant Poisson Structures
In their paper [2], the authors introduced the notion of H-invariant Poisson structures. That is, a special case of a G-invariant structure when G in the finite Heisenberg group and ℛ is the polynomial algebra. Let us remember this notion.
Let V be a complex vector space of dimension n and e0, …, en−1 a basis of V. Take the nth primitive root of unity ɛ = e2πi/n.
From now on, we assume that V = ℂn, with x0, x1, …, xn−1 as a basis and consider the coordinate ring ℂ[x0, x1, …, xn−1].
The τ invariance is, in some sense, a “discrete” homogeneity.
Proposition 2.2 (see [2].)The Sklyanin-Odesskii-Feigin Poisson algebras qn,k(ℰ) are H-invariant Poisson algebras.
Therefore, an H-invariant Poisson structures on the polynomial algebra ℛ includes as the Sklyanin Poisson algebra or more generally of the Odesskii-Feigin Poisson algebras.
In this paper, we are interested in the intersection of the two classes of generalizations of Artin-Shelter-Tate-Sklyanin Poisson algebras: JPS and H-invariant Poisson structures.
Proposition 2.3 (see [2].)If {·, ·} is an H-invariant polynomial Poisson bracket, the usual polynomial degree of the monomial of {xi, xj} equals to 2 + sn, s ∈ ℕ.
3. H-Invariant JPS in Dimension 3
Proposition 3.1. If P ∈ ℋ is a homogeneous polynomial, then σ · P = P and τϖ(P) = 0.
Proof. Let (i, j, k)∈(ℤ/3ℤ) 3 be a cyclic permutation of (0,1, 2). One has
It gives that σ · P = P.
On the other hand, from (3.2), one has τ − ϖ(P) ≡ i + j + kmod 3. And we get the second half of the proposition.
Proposition 3.2. ℋ is a subalgebra of ℛ.
Proof. Let P, Q ∈ ℋ. It is clear that for all α, β ∈ ℂ, αP + βQ belongs to ℋ.
Let us denote by {·, ·} F the JPS associated with the polynomial F ∈ ℛ. It is easy to verify that {xi, xj} PQ = P{xi, xj} Q + Q{xi, xj} P. Therefore, it is clear that the H-invariance condition is verified for the JPS associated to the polynomial PQ.
We endow ℋ with the usual grading of the polynomial algebra ℛ. For F, an element of ℛ, we denote by ϖ(F) its usual weight degree. We denote by ℋi the homogeneous subspace of ℋ of degree i.
Proposition 3.3. If 3 does not divide i ∈ ℕ (in other words i ≠ 3k), then ℋi = 0.
Proof. First of all ℋ0 = ℂ. We suppose now that i ≠ 0. Let P ∈ ℋi, P ≠ 0. Then, ϖ(P) = i. It follows from Proposition 2.3 and the definition of the Poisson brackets that there exists s ∈ ℕ such that ϖ(xi, xj) = 2 + 3s. The result follows from the fact that ϖ(xi, xj) = ϖ(P) − 1.
Set , where . We suppose that ϖ(P) = 3(1 + s). We want to find all α0, α1, α2 such that P ∈ ℋ and, therefore, the dimension ℋ3(1+s) as ℂ-vector space.
Proposition 3.4. There exist s′, s′′, and s′′′ such that
Proof. This is a direct consequence of Proposition 3.3.
Proposition 3.5. The system equation (3.4) has as solutions the following set:
Remark 3.6. For r = 1, one obtains the Artin-Schelter-Tate Poisson algebra which is the JPS given by the Casimir , α, β ∈ ℂ. Suppose that α ≠ 0, then it can take the form
Put deg y0 = 2; deg y2 = 1; deg y2 = 3. Then, the polynomial is also homogeneous in (y0; y1; y2) and defines an elliptic curve in the weighted projective space 𝕎P2;1;3.
The similar change of variables
These structures had appeared in [1], their Poisson cohomology was studied by Pichereau [14], and their relation to the noncommutative del Pezzo surfaces and Calabi-Yau algebras were discussed in [15].
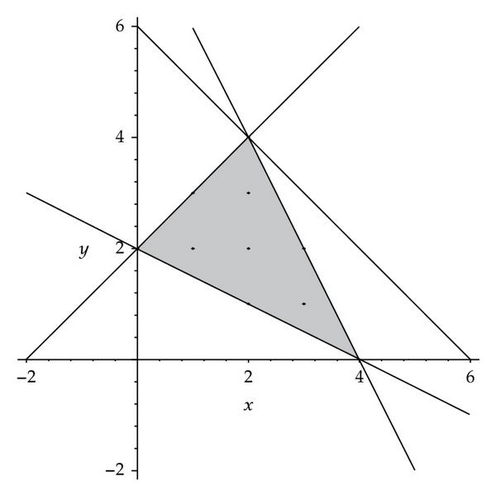
Proposition 3.7. The subset of ℝ2 given by the system (3.6) is a triangle 𝒯r with (0, r), (r, 2r), and (2r, 0) as vertices. Then, dim ℋ3r = Card(𝒯r∩ℕ2).
Remark 3.8. For r = 2, the case of Figure 1, the generic Heisenberg-invariant JPS is given by the sextic polynomial
This new JPS should be considered as the “projectively dual” to the Artin-Schelter-Tate JPS, since the algebraic variety ℰ∨ : P∨ = 0 is generically the projective dual curve in ℙ2 to the elliptic curve
To establish the exact duality and the explicit values of the coefficients, we should use (see [16, chapter 1]) Schläfli′s formula for the dual of a smooth plane cubic ℰ = 0 ⊂ ℙ2. The coordinates of a point satisfies to the sextic relation ℰ∨ = 0 if and only if the line x0p0 + x1p1 + x2p2 = 0 is tangent to the conic locus 𝒞(x, p) = 0, where
Set 𝒮r = 𝒯r∩ℕ2. , and . .
Proposition 3.9.
Proof. Let α ∈ {0, …, r}, and set . Therefore,
It is easy to prove that
Proposition 3.10.
Proof. Let α ∈ {r + 1, …, 2r}, and set . Therefore,
It is easy to prove that
Theorem 3.11.
Corollary 3.12. The Poincaré series of the algebras ℋ is
Remark 3.13. For r = 2, the case of Figure 1, our formula gives the same answer like the classical Pick′s formula for integer points in a convex polygon Π with integer vertices on the plane ([17, chapter 10])
This remark gives a good hint how one can use the developed machinery of integer points computations in rational polytopes to our problems.
4. H-Invariant JPS in Any Dimension
In order to formulate the problem in any dimension, let us remember some number theoretic notions concerning the enumeration of nonnegative integer points in a polytope or more generally discrete volume of a polytope.
4.1. Enumeration of Integer Solutions to Linear Inequalities
In their papers [18, 19], the authors study the problem of nonnegative integer solutions to linear inequalities as well as their relation with the enumeration of integer partitions and compositions.
Define the weight of a sequence λ = (λ0, λ2, …, λn−1) of integers to be |λ | = λ0 + ⋯+λn−1. If sequence λ of weight N has all parts nonnegative, it is called a composition of N; if, in addition, λ is a nonincreasing sequence, we call it a partition of N.
4.2. Formulation of the Problem in Any Dimension
We will denote by P the particular Casimir of the Poisson structure π(P1, …, Pn−2). We suppose that each Pi is homogeneous in the sense of τ-degree.
Proposition 4.1. Consider a JPS π(P1, …, Pn−2) given by homogeneous (in the sense of τ-degree) polynomials P1, …, Pn−2. If π(P1, …, Pn−2) is H-invariant, then
Proof. Let i < j ∈ ℤ/nℤ, and consider the set Ii,j, formed by the integers i1 < i2 < ⋯<in−2 ∈ ℤ/nℤ∖{i, j}. We denote by Si,j the set of all permutation of elements of Ii,j. We have
We can deduce, therefore, that
Proposition 4.2. ℋ is a subvector space of ℛ. It is subalgebra of ℛ if l = 0.
We endow ℋ with the usual grading of the polynomial algebra ℛ. For Q, an element of ℛ, we denote by ϖ(Q) its usual weight degree. We denote by ℋi the homogeneous subspace of ℋ of degree i.
Proposition 4.3. If n is not a divisor of i (in other words, i ≠ nm) then ℋi = 0.
Proof. It is clear the ℋ0 = ℂ. We suppose now that i ≠ 0. Let Q ∈ ℋi, Q ≠ 0. Then,
Set . We suppose that ϖ(Q) = n(1 + s). We want to find all α0, α1, …, αn−1 such that Q ∈ ℋ and, therefore, the dimension ℋ3(1+s) as ℂ-vector space.
Proposition 4.4. There exist s0, s1, …, sn−1 such that
Proof. That is, the direct consequence of the fact that τ − ϖ(σ · Q) = τ − ϖ(Q) = l.
One can easily obtain the following result.
Proposition 4.5. The system equation (4.12) has as a solution
The first one is exactly as in the case of dimension 3. The constraint (4.16) is equivalent to say that
In dimension 3, one obtains the triangle in ℝ2 given by the vertices A(0,2r), B(r, 2r), and C(2r, 0) (see Section 3).
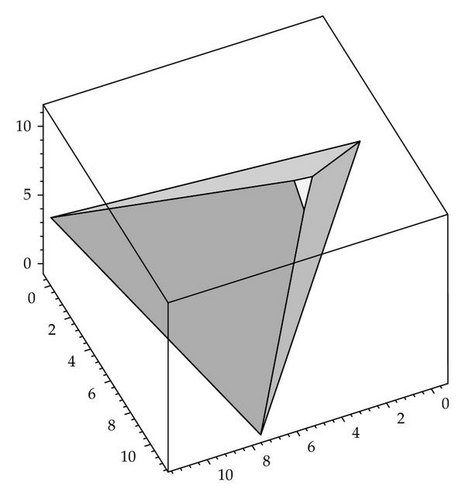
In dimension 4, we get the following polytope (see Figure 2).
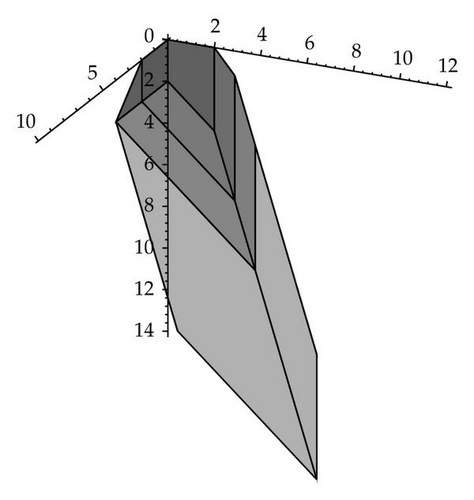
(See Figure 3).
Acknowledgments
The authors are grateful to M. Beck and T. Schedler for useful and illuminative discussions. This work has begun when G. Ortenzi was visiting Mathematics Research Unit at Luxembourg. G. Ortenzi thanks this institute for the invitation and for the kind hospitality. A Part of this work has been done when S. R. T. Pelap: was visiting Max Planck Institute at Bonn. S. R. T. Pelap thanks this institute for the invitation and for good working conditions. S. R. T. Pelap have been partially financed by “Fond National de Recherche (Luxembourg)”. He is thankful to LAREMA for a kind invitation and a support during his stay in Angers. V. Rubtsov was partially supported by the French National Research Agency (ANR) Grant no. 2011 DIADEMS and by franco-ukrainian PICS (CNRS-NAS) in Mathematical Physics. He is grateful to MATPYL project for a support of T. Schedler visit in Angers and to the University of Luxembourg for a support of his visit to Luxembourg.




