International Journal of Mathematics and Mathematical Sciences
Volume 2011, Issue 1 230939
Review Article
Open Access

On Algebraic Approach in Quadratic Systems

Matej Mencinger, 

Corresponding Author

Matej Mencinger

Department of Basic Science, Faculty of Civil Engineering, University of Maribor, Smetanova 17, 2000 Maribor, Slovenia uni-mb.si

Department of Mathematics, Institute of Mathematics, Physics and Mechanics Ljubljana, 1000 Ljubljana, Jadranska 19, Slovenia

Search for more papers by this author
First published: 06 April 2011
https://doi.org/10.1155/2011/230939
Citations: 1
Academic Editor: Ivan Chajda

Abstract

When considering friction or resistance, many physical processes are mathematically simulated by quadratic systems of ODEs or discrete quadratic dynamical systems. Probably the most important problem when such systems are applied in engineering is the stability of critical points and (non)chaotic dynamics. In this paper we consider homogeneous quadratic systems via the so-called Markus approach. We use the one-to-one correspondence between homogeneous quadratic dynamical systems and algebra which was originally introduced by Markus in (1960). We resume some connections between the dynamics of the quadratic systems and (algebraic) properties of the corresponding algebras. We consider some general connections and the influence of power-associativity in the corresponding quadratic system.

1. Introduction

The stability of hyperbolic critical points in nonlinear systems of ODEs is well-known. It is described by the stable manifold theorem and Hartman′s theorem. The critical (or equilibrium or stationary or fixed) point of or is defined to be the solution of the following algebraic (system of) equation(s), or , respectively. For the systems of ODEs, , the critical point is said to be hyperbolic if no eigenvalue of the corresponding Jacobian matrix, , of the (nonlinear vector) function f has it is eigenvalue equal to zero (i.e., Re(λi) ≠ 0). In case of discrete system, , the critical point is said to be hyperbolic if no eigenvalue of the Jacobian matrix has it is eigenvalue equal to 1 (i.e., |λi| ≠ 1). Roughly speaking, if for a continuous system Re(λi) < 0 for every λi, the corresponding critical point is stable (it is unstable, if Re(λi) > 0 for some λi). Similar, if for discrete systems |λi| < 1 for every λi, the corresponding critical point is stable (it is unstable, if |λi| > 1 for some λi). Note that just one eigenvalue of the corresponding linear approximation of or for which Re(λi) = 0 or |λi| = 1, respectively, implies that the stability must be investigated separately in each particular case (because of the significance of the higher order terms). Such articles where for the non-hyperbolic critical points the classes of stable and unstable systems are considered are published constantly. (The authors consider the influence of at least quadratic terms added to the linear ones.) The most recent article on quadratic systems might be [1]. For homogeneous quadratic systems the origin is an example of the so-called totally degenerated (i.e., non-hyperbolic) critical point.

In this paper the algebraic approach to autonomous homogeneous quadratic continuous systems of the form and autonomous homogeneous quadratic discrete dynamical systems of the form (where Q : IRn → IRn is homogeneous of degree two in each component: for each (real) a) is considered, as suggested by Markus in [2]. Markus idea was to define a unique algebra multiplication via the following bilinear form :
(1.1)
in order to equip IRn with a structure of a (nonassociative in general) commutative algebra (A, *). In the corresponding algebra (A, *) the square of each vector is equal to
(1.2)
Thus, the system obviously becomes a Riccati equation and many interesting relations follow.

In the sequel we consider the existence of some special algebraic elements (i.e., nilpotents of rank 2 and idempotents), as well as the reflection of algebra isomorphisms in the corresponding homogeneous quadratic systems, which represents the basis for the linear equivalence classification of homogeneous quadratic systems. It was already used by the author in order to analyze the stability of the origin in the continuous case in IR2 and in IR3 (the origin is namely a total degenerated critical point for in any dimension n [3]).

However, in the discrete case the origin is obviously a super stable critical point, since the Jacobian evaluated at the origin is the zero matrix and consequently it is eigenvalues are all zero. On the other hand the dynamics in discrete systems can readily become chaotic in some special regions of the space even in 1D (cf. [4, Section 8]) and it is well-known [5] that the dynamics on the unit circle (which contains the fixed point (1,0) is chaotic for
(1.3)
Note that system (1.3) is a homogeneous quadratic (i.e., of the form ) for
(1.4)

The interested reader is invited to consult, for example, [6–10] to obtain some further informations.

Let us conclude the introduction with two examples in order to explain the one to one connection defined by (1.1). Let us consider system (1.3) and it is continuous analogue: x′ = x2 − y2, y′ = 2xy. Their corresponding quadratic form is Q(x, y) = (x2 − y2, 2xy). Using (1.1) one obtains the following multiplication rule:
(1.5)

Thus, in the standard basis e1 = (1,0) and e2 = (0,1) the multiplication table for the corresponding algebra is as illustrated in Table 1.

* e1 e2
e1 e1 e2
e2 e2 −e1

Applying the substitution (i.e., the algebra isomorphism) e1 → 1, e2 → i one obtains as illustrated in Table 2 which is readily recognized as the algebra of complex numbers.

  *   1     i  
  1     1     i  
  i     i      − 1  

On the other hand, beginning, for example, with the algebra A   = (IR3, *) given with the multiplication table as illustrated in Table 3 the corresponding quadratic form is obtained again by applying .

* e1 e2 e3
e1 e1 e2 e3
e2 e2 −e1 0
e3 e3 0 −e1
By denoting , we get
(1.6)
Thus, we obtain the following quadratic systems
(1.7)

2. Some Connections between Systems and Their Corresponding Algebras

First note that the algebra which corresponds to a system or is always commutative, since from (1.1), it follows
(2.1)
However, the corresponding algebra is generally not associative. For instance for algebra A = (IR3, *) in the above example from Table 3 one can readily observe
(2.2)
Obviously, the correspondence (1.1) between system and algebra is unique. Note also that there is a one-to-one correspondence between homogeneous systems of degree m and the corresponding m-ary algebras. In this paper we stay within the domain m = 2, but the interested reader is referred to [10, 11] for further informations (in case m > 2).

In order to achieve better understanding let us recall some definitions from the dynamical systems and algebra theory. A subset W⊆A which is closed for algebraic multiplication (i.e., for every pair w1, w2 ∈ W we have w1*w2 ∈ W) is called a subalgebra. For example, if the corresponding vector space is a direct sum of two (vector) subspaces (i.e., V = V1 ⊕ V2) and if A1 = (V1, *) and A2 = (V2, *), then A = A1 ⊕ A2 = (V1 ⊕ V2, *) contains two nontrivial subalgebras A1 and A2. To every one can associate a subalgebra , defined by products , , , , , , , and so on and their linear combinations, which is called the subalgebra generated by the element . A subalgebra I⊆A is called (left and right) ideal of algebra A, if AI⊆I and IA⊆I (i.e., for every i ∈ I and every we have and ). Every algebra A = (V, *) has at lest two ideals, the trivial ideals V and {0}. Furthermore, the set A2 = A*A defined as the subspace of all linear combinations of products in A is obviously an ideal of A.

The map ϕ : A → B is homomorphism from algebra (A, *) into algebra (B, ∘), if and only if, for every pair of vectors from algebra A we have: . If there is a homomorphism from algebra A to algebra B they are called homomorphic. A bijective homomorphism is called an isomorphism and the corresponding algebras are called isomorphic (in this case m = n). By S* and S∘ let us denote the corresponding quadratic (continuous or discrete) systems. The map h : IRn → IRn preserves solutions from system into system if and only if it takes parametrized solutions of the first system into parametrized solutions of the second one (i.e., is a solution of system S∘, whenever is a solution of S*. In discrete systems the solutions, ; k = 0,1, 2, … are called orbits. By preserving of orbits we mean that ; k = 0,1, 2, … is an orbit of system S∘, whenever ; k = 0,1, 2, … is an orbit of system S*.

Element of algebra (A, *) is said to be a nilpotent of rank 2, if and it is said to be an idempotent, if . If for some point the algebraic equation or is fulfilled, it is called critical point of system or , respectively. The solution is a ray solution of if for every time t vector remains on the line .

2.1. Algebraic Isomorphism and Linear Equivalence

The basic correspondence (1.1) between quadratic systems and algebras is the same for as well for . The basic property concerning the linear equivalence between quadratic systems is also very similar as shown in the following two Propositions.

Proposition 2.1. Let ϕ : IRn → IRm be linear. Then ϕ preserves solutions from system ; into system ; if and only if ϕ is a homomorphism from algebra A* = (IRn, *) into algebra A∘ = (IRm, ∘).

Proof. Let ϕ be some linear map which preserves solutions from S* into S∘. And let A* = (IRn, *) and A∘ = (IRm, ∘) be the corresponding algebras. Let be the solution of S* and let be the solution of S∘. Thus and and from one obtains . Since ϕ is linear it is Jacobian is equal to ϕ in every point of the space (i.e., ϕ′ = ϕ). Therefore for every . Substituting and applying commutativity and bilinearity of multiplications ∘ and *, we obtain , for all . Since ϕ is linear by assumption, this yields that ϕ is a homomorphism from A* = (IRn, *) into A∘ = (IRm, ∘).

Conversely, let ϕ be homomorphism from A* = (IRn, *) into A∘ = (IRm, ∘). Thus, for all we have . For we readily obtain: . Using again ϕ′ = ϕ, we obtain

(2.3)
Let be a solution of S*. We want to prove that is a solution of S∘. Using and (2.3) and the chain rule for the derivative one obtains , which means that is a solution of S∘. This completes the proof.

Proposition 2.2. Let ϕ : IRn → IRm be linear. Then ϕ preserves orbits from system ; into system ; if and only if ϕ is a homomorphism from algebra A* = (IRn, *) into algebra A∘ = (IRm, ∘).

The proof is very similar to the proof of Proposition 2.1 and will be omitted here.

The use of Propositions 2.1 and 2.2 is quite similar. In the following Example the use of Proposition 2.1 is considered.

Example 2.3. Systems

(2.4)
are isomorphic. The corresponding isomorphism from (x, y) into (X, Y) is
(2.5)
Note that system S(x,y) is much easier to treat than S(X,Y). The only idempotent of S(x,y) is (x = 1, y = 0), while the only idempotent of S(X,Y) is (X = 2, Y = −5/2). It is obtained as the solution to algebraic system of equations
(2.6)
The particular solutions with the initial conditions near idempotent (the black line) in both cases yield the solution curves (the red line) shown in Figures 1 and 2. Figures 1, 2, 3, and 4 are clearly indicating that the dynamics of system S(x,y) is much easier to understand. Note that in the Markus theory system S(x,y) is a kind of normal form (i.e., the class representative) of it is class (i.e., of all isomorphic systems). For the entire list of “normal forms” in 2D please refer to [2, Theorems 6, 7, and 8].

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The particular solution to S(X,Y).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The particular solution to S(x,y).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The phase diagram basis for S(x,y).
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The phase diagram basis for S(X,Y).

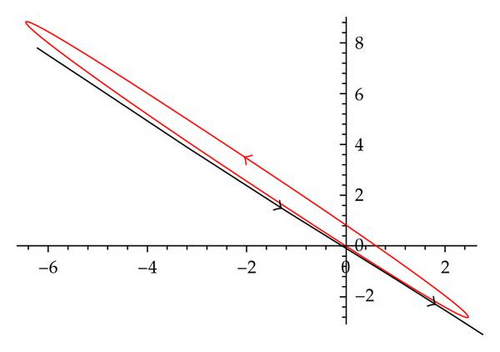
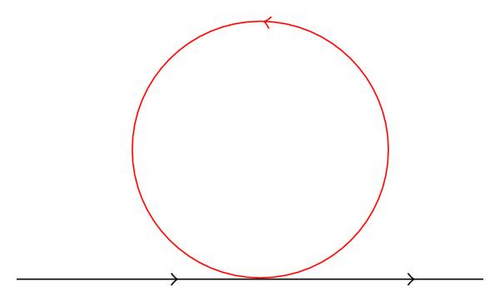
The immediate corollary is that systems S* and S∘ are linearly equivalent if and only if their corresponding algebras A* and A∘ are isomorphic.

2.2. Algebraic Structure and Reductions of the System

The above-mentioned corollary and the so-called Kaplan-Yorke theorem is a basement of algebraic treatment of homogeneous quadratic systems using algebraic classification of the commutative algebras. The following algebraic result due by Kaplan and Yorke [12] affects strongly on the dynamics of homogeneous quadratic systems.

Theorem 2.4 (Kaplan-Yorke). Every real finite dimensional algebra A* = (IRm, *) contains at least one nonzero idempotent or a nonzero nilpotent of rank two.

For proof please refer to the original paper [12].

Concerning the existence of a subalgebra, we have the following result.

Proposition 2.5. A homogeneous quadratic system S* has an invariant r-dimensional linear subspace Er if and only if the corresponding algebra has an r-dimensional subalgebra.

Remark 2.6. We present just the proof for discrete case (i.e., when ; . The proof for continuous system ; can be found, for example, in Markus [2].

Proof. Let Er = span (e1, e2, …, er) be an invariant r-dimensional linear subspace of a n-dimensional vector space V, n > r. Then for every the orbit is contained in Er. We will prove that (Er, *) is the r-dimensional subalgebra (i.e., the subspace Er is closed for multiplication *). Setting we have ei*ei ∈ Er for every 1 ≤ i ≤ r. Now we want to prove that ei*ej ∈ Er for all 1 ≤ i, j ≤ r. In order to prove this, let us set and compute using the commutativity rule in algebra

(2.7)
Since , ei*ei ∈ Er, and ej*ej ∈ Er it follows also ei*ej ∈ Er which means that for every pair the product is contained in Er, as stated. The converse follows directly from the fact that for every , since Er is a subalgebra, we have . Setting we immediately obtain that . Setting one obtains , and so on. Thus the orbit is contained in Er, which means that Er is invariant, as stated.

Concerning the existence of a subalgebra and an ideal in the corresponding algebra let us mention the following result, (for proof please refer to [10]).

Proposition 2.7. Let I be an ideal of algebra A* and W a subagebra such that V = I ⊕ W. Then the solution of the initial value problem of the corresponding quadratic system with the initial value problem can be solved by successive solution of

(2.8)
where w(t) is a solution of the first subsystem in W.

Corollary 2.8. A system with the initial condition splits into two separated subsystems

(2.9)
if and only if the corresponding algebra can be written as a direct sum of two nontrivial ideals
(2.10)

Proof. Apply I = I1 and W = I2 in the previous result and take into consideration that I1, I2 are both ideals which means that 2w(t)*i = 0 in the second equation of Proposition 2.7. This finishes the proof.

The last two results are further examples where exactly analogous results can be formulated for the discrete case. Note that the reduction and/or splitting of the system is of great importance when exact solutions are needed.

2.3. Special Algebraic Elements and (In)Stability

However, some connections between the system and corresponding algebra (A, *) differs in the continuous and discrete case. For example the correspondence between ray solutions/fixed points and idempotents/nilpotents. Let us first recall the Lyapunov definition of stability.

Definition 2.9. Critical point of system is said to be stable if and only if for every ε > 0 there is a δ > 0 such that for every initial condition for which and for every time t > 0 for which the solution with the initial condition is defined, we have

(2.11)
In the next theorem the well-known necessary conditions for the stability of the origin in are given.

Theorem 2.10. If an algebra A* contains an idempotent , then the origin in the corresponding system is unstable critical point.

Proof. First note that is always a subalgebra of A*. Thus (by Proposition 2.5), the flow is invariant. Since from (when inserting ) one obtains 1-dimensional ODE f′(t) = f2(t). Next observe that is in every neighborhood of the origin. Therefore the solution with the initial condition (i.e., f(0) = ε) is

(2.12)
Finally observe that which completes the proof.

Note that the immediate corollary of Theorem 2.10 and the Kaplan-Yorke theorem is that systems with the stable origin always contain some nilpotents of rank two. In the continuous case the ray-solutions are as proven in Theorem 2.10 related with the existence of the idempotent. However, in the discrete case the existence of idempotent simply means the existence of the fixed point.

On the other hand, the existence of a nilpotent of rank two implies the existence of line of critical points in the continuous case, since from one obtains for every realα. However, in the discrete case the above property yields the existence of the ray-solution, since from one readily obtains that for every real α.

3. Conclusions

For the stability analysis of the origin in systems some new results are needed, for example, results obtained Markus approach in [13, 14]. Using Markus original classification one can obtain that only (up to linear equivalence) three (families of) systems admit stable origin in 2D. These systems are (cf. [13]):
(3.1)
In order to obtain similar result(s) in IR3 and/or in IRn for n > 3 a partial algebraic classification (of systems/algebras with a plane of critical points) similar to Markus was done in (cf. [14]). Roughly speaking (cf. [13]), the existence of complex idempotents overlapping with the existence of the so-called essential nilpotents (i.e., nilpotents which are not contained in the linear span of all complex idempotents) seem to define (algebraically) the stability of the origin. The conjecture was confirmed by examining the complexification
(3.2)
of real algebras A* corresponding to the systems with a plane of critical points as well as on the so-called homogenized systems in IR3 (cf. [15]). It seems that [13] the spectral analysis of linear operator defined by (i.e., multiplication by essential nilpotent ) is playing an important role in stability of the origin in systems .

However, algebraic approach is recently used (cf. [8, 9]) also in order to consider planar homogeneous discrete systems in the sense of (non)chaotic dynamics. The results are showing that the dynamics of systems whose corresponding algebras are containing some nilpotents of rank 2 cannot be chaotic [9]. Furthermore, system (1.3) is one of the simplest systems with chaotic dynamics and the corresponding algebra A(2) is power-associative. Note that every orbit of system which corresponds to a power-associative algebra can be obtained in terms of an orbit of a corresponding linear system. Namely, given an initial point the orbit of can be obtained in terms of , since in the power-associative algebras the powers of every are well defined (i.e., ). In case of system (1.3) the left multiplication matrix of (by ) is obtained from .

In the chaotic region where , the corresponding multiplication matrix has the form
(3.3)
Readily, if ϕ = kπ where k is a rational number, then the point (cos ϕ, sinϕ) is periodic. On the other hand, if ϕ = Kπ where K is irrational, the orbit of (cos ϕ, sinϕ) is dense on the unit circle but not periodic. Furthermore, the points (cos ϕ, sinϕ) (where ϕ = kπ and k is a rational number) are dense in , as well. Thus there is chaos on . The question is whether the other power-associative algebras also correspond to the systems with chaotic dynamics.
Finally, note that in the continuous case one can observe the following: the solution to with the initial condition can be expressed explicitly by the following formula:
(3.4)
where I is the identity matrix and is the linear operator defined by the (left) multiplication by . The proof of the above explicit formula is a direct computation and can be found in [7], where (3.4) is used to prove that in power-associative algebras the corresponding system cannot have periodic solutions. Another interesting question (when considering power-associativity together with continuous quadratic systems) is whether one can use (3.4) in order to obtain some results on stability of the origin in IRn (n ≥ 2).

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.