The present paper aims to compare Harrington′s direct method of moment (MoM) with the conjugate gradient method (CGM) by evaluating the total current solving the electric field integral equation (EFIE). Based on their performances, the number of iterations needed for convergence, storage, and the level of precision, it is found that the direct MoM is more efficient than other iterative CGM.

1. Introduction

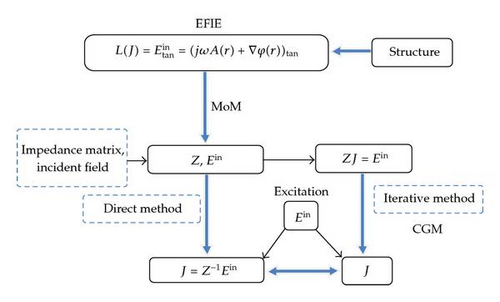
In this paper, we consider the integral electromagnetic field equation (EFIE) for computing the total current distribution on antenna surfaces, and we study the two standard methods by comparing the solutions. These methods are the direct method of moment (MoM for short) developed by Harrington [1] and the iterative conjugate gradient method (CGM) [2]. This comparative study, which is done at the level of numerical solutions, is achieved in terms of computational advantages and disadvantages as well as their ability to determine the current distributions on metal surfaces. Based on their performance, the number of iterations needed for convergence, the storage, and the level of precision, it comes out from our analysis, developed in the next sections, that the direct method MoM is more efficient than other iterative CGM.

Recall that the electromagnetic field has been successfully used in the computation of the current distribution over the surface with few geometries yielding analytic solutions. To deal with the study of the above-mentioned integral electromagnetic field equation, the most popular method for getting numerical solutions is given by the method of moment with advantages and disadvantages. Regarding the disadvantages of this approach, we mention the one related to the convergence problem and the second connected with the restriction of the explicit storage of a the dense matrix. Furthermore, the monotonic convergence in the MoM solution can be achieved under only stringent condition which are difficult to realize in case of complex problems [2]. In attempt to address the above disadvantages of the direct MoM, another alternative approach has been suggested; this concerns the CGM for solving iteratively the electromagnetic problem [3, 4]. Since then, CGM has been successfully applied to a number of radiation and scattering problems and has been quite popular because of the O(N) memory requirement. Using discretization of EFIE in the framework of the MoM to get the impedance matrix Z [5], Sarkar and Rao applied to the Z matrix the CGM of steepest descent to calculate the charge distribution over conducting surfaces [6]. However, few attempts have been done to apply CGM to electrostatic problems involving conducting surfaces. The presentation of this paper is as follows: in Section 2, we give some generalities on EFIE. In Section 3, we review some useful aspects on the method of moment. In Section 4, we describe the algorithm of the CGM. In Section 5, we work out the numerical solutions of EFIE using both MoM and CGM. Last section is devoted to the conclusion.

2. Generalities on EFIE

Electromagnetic field has been successfully used in the computation of finding the current distribution over the surface. Solving current distributions on metal surface usually incorporates formulation of EFIE (electric field integral equation) [7]. Few geometries yields solutions (analytical, numerical approximation) have been successfully used. But most of the popular method is the method of moment.

By the method the initial operator equation can be formulated by employing boundary condition for tangential incident (Eⁱⁿ) and impressed (E^sc) electric field;

(2.1)

Scattering or radiation problems are essentially identical, the only difference is that the “incident” field for the driven antenna is the applied electric field in the feed. The total electric filed is a combination of the incident field and the scattered field,

(2.2)

The incident electric field is either the incoming signal or the excitation electric field ion the antenna feed. The scattered electric field E^sc is due to surface currents and free charges on the metal surface S,

(2.3)

The magnetic vector potential A(r) describes surface current radiation whereas the electric potential ϕ(r) describes radiation of surface. Free charges are

(2.4)

respectively, and the three-dimensional Green′s function is

(2.5)

where R = |r − r^′|. The electric field integrodifferential equation for the induced current is obtained by requiring that the total tangential electric field, E_tan, vanishes on the conductor surface S, thus, giving the electric field integral equations by (2.1),

(2.6)

The corresponding weak form of the equation is obtained by testing it with a vector-valued weighting function f_m(r) defined on and tangent to S. Using the identity ∇·(f_mϕ) = ϕ∇·f_m + ∇ϕ · f_m and the divergence theorem, the term involving the scalar potential is integrated by parts to obtain the weak form

(2.7)

Concerning the surface current density, J is expanded into the basis functions in the form

, and using f_m (m = 1,2, …, N) as a test function, the moment equations are obtained below:

(2.8)

where V_m = ∫_sf_m · EⁱⁿdS,

(2.9)

The square impedance matrix determines electromagnetic interaction between different segments elements.

3. Useful Tools on MoM

The method of moments (MoM) is a well-known technique for solving linear equations. In antenna analysis, the MoM is used to convert the electric field integral equation into a matrix equation or system of linear equations (Harrington, 1968) [1]. Let us consider the inhomogeneous equation:

(3.1)

where L is a linear operator, g is known, and f is to be determined (is the unknown function). We will now perform the two essential steps we have highlighted above. In order to create the matrix equation, the unknown function is defined to be the sum of a set of known independent functions, f_n, called basis or expansion functions with unknown amplitudes, α_n.

(i)
Firstly, let the basis functions be f₁, f₂, …, f_N. The unknown function f is expanded in terms of a linear combination of these basis functions:
(3.2)
The linear combination of f_n should represent the unknown f in the domain. Substitute (3.1) into (2.9), we have that, upon using the linearity of the operator L, the unknown amplitudes can be brought out of the operator giving
(3.3)
where α₁, α₂, …, α_N are unknown coefficients that have to be determined.
(ii)
Secondly, we define a set of N weighting functions (testing functions), ω₁, ω₂, …, ω_N, which are integrated with (3.3) to give m different linear equations, and take the inner product of the previous equation with ω_m:
(3.4)
The system can now be written in matrix form as
(3.5)
where
(3.6)
If the matrix A_mn is not singular, the unknowns α_n are simply given by
(3.7)
and the original function f can be reconstructed using (3.3). We can now generalize the following definitions.

Basis Functions Basis functions can use full domain functions such as special functions, polynomials, and so forth. A set that is useful for practical problem is the subsectional basis function. This means that each f_n is only nonzero over a subsection of the domain of f. A common choice is the pulse function:

(3.8)

Weighting Functions (Testing Functions) Two common choices are as follow.

(i)
Point matching: taking Dirac delt δ functions as testing functions ω_m(x) = δ(x − x_m) where m = 1,2, …, N.
(ii)
Galerkin Method: if we used the same function for both the basis and weighting f, that is. If we used the same function for both f_n(x) = ω_n(x) where n = 1,2, …, N.

4. Conjugate Gradient Method

The conjugate gradient method is the most prominent iterative method for solving sparse systems of linear equations. It is applied to the analysis of radiation from thin wire antennas. With this iterative technique, it is possible to solve electrically large arbitrarily oriented wire structures without storing any matrices as is conventionally done in the method of moments. The basic difference between the proposed method and Galerkin′s method, for the same expansion functions, is that for the iterative technique we are solving a least squares problem. The conjugate gradient method (CGM) is an algorithm for the iterative solution of an operator equation of the form

(4.1)

set in a Hilbert space. If A is positive definite, the classical CGM converges to the exact solution in at most N steps in an N-dimensional space, and it proceeds as follows [2, 8]:

(4.2)

It has been shown [8] that sequence of solution {x_n} generated by this algorithm minimizes the error function

(4.3)

where h is the exact solution.

5. Numerical Results

The results are given through two examples concerning straight wire scatterers.

5.1. First Example

As a first example of a straight-wire scatterer, we consider the simple straight-wire scatterer of length l = 0.5λ and radius a = 0.001λ. The scatterer is excited by a plane wave with a 45° angle of incidence; this example has been taken from a well-known book [7]. Figure 1 show the computed currents (direct solution MoM) according to Pocklington equations compared with conjugate gradient method. In these figures, we present the result for the current distribution along the antenna that we obtain through our own developments using MATLAB. This comparison shows that the movement is retained with some minor differences in middle of the curve. Notice that our result (under MATLAB) agrees with the one published in [9]. Notice also that one of the essential tasks in our way of doing is the use of the moment method and the choice of test and basis functions.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Current distributions: comparison of results for the MoM and CGM currents. On the left current distribution for a 0.5λ length dipole antenna and on the right a current distribution for a 1.2λ length dipole antenna.

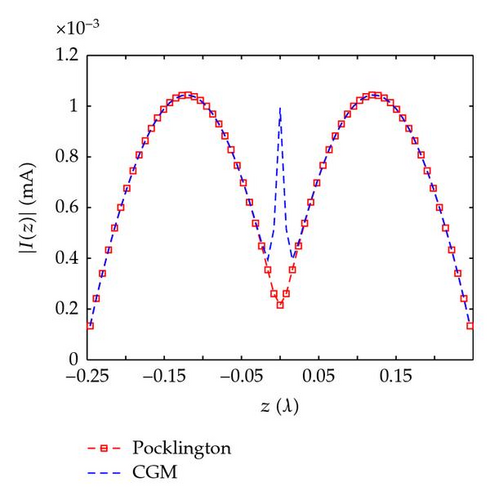
5.2. Second Example

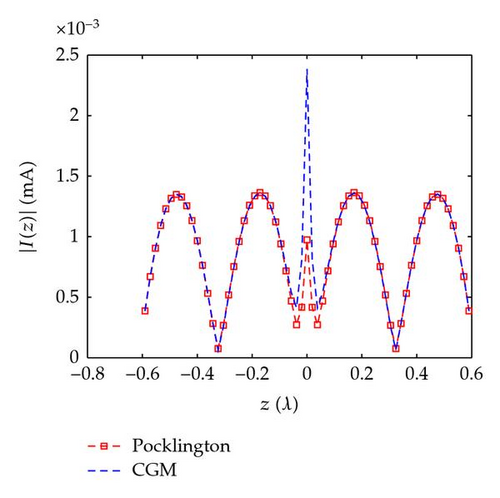
In this example we consider the scattering from the straight-wire scatterer of length l = 1.2λ and radius a = 0.001λ shown in Figure 2; the current has a delta-gap compared with the sinusoidal current I(z) = Asink(h−|z|) and with the current found by CGM.

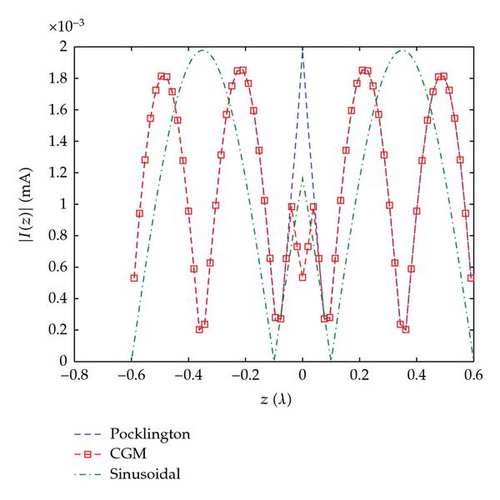
6. Conclusion

In this paper, we have presented a comparative study of the direct method of moment and the iterative conjugate gradient method. These methods are used to solve the differential linear equations; in particular, the integral electromagnetic field equation (EFIE) for computing the total current distribution. Based on their performances, the number of iterations needed for convergence, storage, and the level of precision, we have found that the direct MoM is more efficient than other iterative CGM.

Acknowledgments

The author would like to thank professor E. H Saidi for helpful discussions and URAC 09 for support.

References

1 Harrington R. F., Field Computation by Moment Methods, 1968, Macmillan, New York, NY, USA.
Google Scholar
2 Sanjaynath V. V., Balakrishnan N., and Nagabhushana G. R., Application of conjugate gradient method for static problems involving conductors of arbitrary shape, IEEE Transactions on Antennas and Propagation. (1994) 42, no. 7, 1028–1033, https://doi.org/10.1109/8.299609.
10.1109/8.299609
Web of Science® Google Scholar
3 Sarkar T. K. and Rao S. M., The application of the conjugate gradient method for the solution of electromagnetic scattering from arbitrarily oriented wire antennas, IEEE Transactions on Antennas and Propagation. (1984) 32, no. 4, 398–403.
10.1109/TAP.1984.1143331
Web of Science® Google Scholar
4 Sarkar T. K. and Arvas E., On a class of finite step iterative methods (conjugate directions) for the solution of an operator equation arising in electromagnetics, IEEE Transactions on Antennas and Propagation. (1985) 33, 1058–1066.
10.1109/TAP.1985.1143493
Web of Science® Google Scholar
5 Rao S. M., Glisson A. W., Wilton D. R., and Vidula B. S., A simple numerical solution procedure for statics problems involving arbitrary shaped conductors, IEEE Transactions on Antennas and Propagation. (1979) 27, 604–607.
10.1109/TAP.1979.1142171
Web of Science® Google Scholar
6 Sarkar T. K. and Rao S. M., An iterative method for solving electrostatic problems, IEEE Transactions on Antennas and Propagation. (1982) 30, no. 4, 611–616, https://doi.org/10.1109/TAP.1982.1142833, 666760.
10.1109/TAP.1982.1142833
Web of Science® Google Scholar
7 Harrington R. F., Field Computation by Moment Methods, 1993, Wiley-IEEE Press, New York, NY, USA.
10.1109/9780470544631
Google Scholar
8 Hayes R. M., Iterative methods of solving linear problems on Hilbert space, Contributions to the solution of systems of linear equations and the determination of eigenvalues, 1954, U. S. Deptartment of Commerce, Washington, DC, USA, 71–103, National Bureau of Standards Applied Mathematics Series 39, 0066563.
Google Scholar
9 Barrera-Figueroa V., Sosa-Pedroza J., and López-Bonilla J., Simplification of Pocklington′s integral equation for arbitrary bent thin wires, Boundary Elements XXVII, 2005, 39, WIT Press, Southampton, UK, 563–574, WIT Transactions on Modelling and Simulation, 2234669.
Google Scholar

Citing Literature

All articles

A Comparison of Two Methods for Solving Electromagnetic Field Integral Equation

Abstract

1. Introduction

2. Generalities on EFIE

3. Useful Tools on MoM

4. Conjugate Gradient Method

5. Numerical Results

5.1. First Example

5.2. Second Example

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Comparison of Two Methods for Solving Electromagnetic Field Integral Equation

Abstract

1. Introduction

2. Generalities on EFIE

3. Useful Tools on MoM

4. Conjugate Gradient Method

5. Numerical Results

5.1. First Example

5.2. Second Example

6. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information