Journal of Applied Mathematics
Volume 2011, Issue 1 124590
Research Article
Open Access

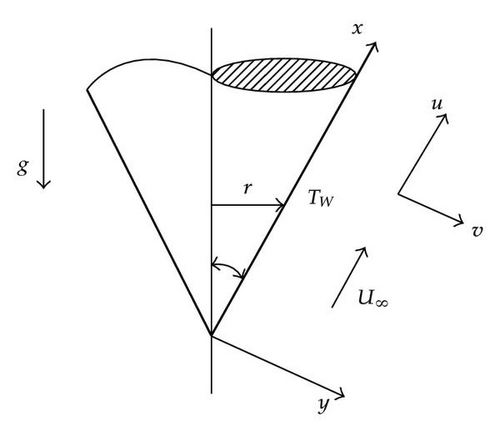
Radiative Mixed Convection over an Isothermal Cone Embedded in a Porous Medium with Variable Permeability

M. F. El-Amin, 

Corresponding Author

M. F. El-Amin

Computational Transport Phenomena Laboratory (CTPL), Division of Physical Sciences and Engineering (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia kaust.edu.sa

Mathematics Department, Aswan Faculty of Science, South Valley University, Aswan 81258, Egypt svu.edu.eg

Search for more papers by this author
N. A. Ebrahiem, 

N. A. Ebrahiem

Mathematics Department, Aswan Faculty of Science, South Valley University, Aswan 81258, Egypt svu.edu.eg

Search for more papers by this author
Amgad Salama, 

Amgad Salama

Computational Transport Phenomena Laboratory (CTPL), Division of Physical Sciences and Engineering (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia kaust.edu.sa

Search for more papers by this author
Shuyu Sun, 

Shuyu Sun

Computational Transport Phenomena Laboratory (CTPL), Division of Physical Sciences and Engineering (PSE), King Abdullah University of Science and Technology (KAUST), Thuwal 23955-6900, Saudi Arabia kaust.edu.sa

Search for more papers by this author
First published: 20 February 2011
https://doi.org/10.1155/2011/124590
Citations: 5
Academic Editor: Zhangxin Chen

Abstract

The interaction of mixed convection with thermal radiation of an optical dense viscous fluid adjacent to an isothermal cone imbedded in a porous medium with Rosseland diffusion approximation incorporating the variation of permeability and thermal conductivity is numerically investigated. The transformed conservation laws are solved numerically for the case of variable surface temperature conditions. Numerical results are given for the dimensionless temperature profiles and the local Nusselt number for various values of the mixed convection parameter χ, the cone angle parameter m, the radiation-conduction parameter Rd, and the surface temperature parameter H.

1. Introduction

The problem of convective heat transfer in porous medium has attracted researchers because of the several applications it incorporates. Examples include enhanced oil recovery, nuclear waste disposal, geothermal reservoirs, and ceramic processing. This topic has been extensively covered in literatures in connection with different geometries, boundary conditions, and media. While most of the cases concern with convection along semi-infinite vertical walls impeded in porous media (e.g., [1–5] and many others) several other geometries were also considered including cylinders (e.g., [6, 7]), wedges (e.g., [8]), spheres (e.g., [9], Huang et al., 1986), cones (e.g., [10]). The presence of thermal radiation was also investigated for the case of truncated cone by Yih [11] and for the case of vertical wall by Abbas et al. [12]. All these studies consider the permeability and conductivity of the medium as constant. However, porosity measurements by Schwartz and smith [13], Tierney et al. [14], and Benenati and Brosilow [15] showed that the porosity in the vicinity of solid objects is not usually constant. In other words, it varies from the wall to the interior of the porous medium which results in variations in the permeability as well as the equivalent thermal conductivity across the medium. Chandrasekhara et al. [16–18], and have incorporated variable permeability when studying convection in porous media and reported its significant impact on the velocity field and heat transfer.

The present paper considers the case of mixed convection and radiation about a cone immersed in a porous medium. It is assumed that the immersion of the cone has caused disturbances to the host porous medium domain resulting in the porosity, the permeability, and the effective thermal conductivity of the neighboring region to vary. This scenario may result during the underground disposal of the high-level nuclear waste contained in canisters of conical shape. That is, the reprocessing of depleted nuclear reactor fuel elements usually results in the formation of considerable quantities of high-level, long-lived radioactive waste. These wastes are usually adopted and cast in metallic cylinders and are stored in canisters which may lately be burred underground. The decay heat generated from the spent nuclear fuel may last for decades and therefore might result in the temperature to be high enough so as to make it important to include radiation heat transfer into consideration.

On the other hand, the inclusion of thermal radiation into the energy equation requires that some care be taken. That is, unlike heat transfer by conduction and convection, thermal radiation is a more complex process because of its spectral and directional dependence in addition to the difficulty of determining accurate physical property values of the medium. Since the energy equation describes a local balance of energy arriving by all modes of energy transfer, internal energy stored, energy generated by sources, and energy leaving by all modes of transfer, the net energy associated with radiative effects can be viewed in the energy equation as a local energy source [19], that is,
()
where D/Dτ is the substantial derivative, β is the thermal coefficient of volume expansion of the fluid, qr is the radiant flux vector, q′′′ is some sort of volumetric energy source, and Φd is the energy production by viscous dissipation. Hence an expression for ∇·qr is needed in terms of the temperature distribution. The Radiative Transfer Equation (RTE) describes the variation of the spectral radiative intensity for an absorbing-emitting-scattering medium in a given direction, s, in the solid angle dω about the s direction as
()
where Iλ(s) is the spectral intensity of the radiation, Iλb is the blackbody intensity, s is the optical coordinate, and ξλ(ω, ω′) is the scattering phase function which represents the distribution of energy after it is scattered. The first term in the right hand side of the above equation represents the loss in spectral radiation intensity by absorption (includes induced emission), the second term represents the gain by spontaneous emission, the third term represents scattering loss, and the last term represents the gain by scattering into s direction. It is apparent that solutions to the above-given system of equations may not be possible, however, certain simplification may be imposed that makes this system amenable to solution. One of these simplifications may be the assumption of optically thick medium in which radiation travels only a short distance before being scattered or absorbed. In this case the local radiation intensity at a point is assumed to only emerge within the neighborhood of that point. For this situation, it is possible to transform the relation of radiative energy into a diffusion-like relationship [19].

2. Analysis

Consider the radiative mixed convection along the surface of a cone immersed in a fluid-saturated porous medium whose properties are assumed to be functions of space (following [16]). Figure 1 describes the physical domain and the coordinate system. The governing equations for this problem may be given as
()
()
()
()
()
()
()
()
where u and v are the velocity components in the x and y-directions, respectively, T, T∞, and Tw  are the temperatures of the fluid, the ambient medium, and the cone surface, respectively, (ρ∞Cp) f is the product of density and specific heat of the fluid, p is the pressure, K0 and ε0 are the permeability and porosity at the edge of the boundary layer, respectively, ζ and ζ* are some constants whose values are taken as 3.0 and 1.5, respectively, (see [16]), β, μ, and ρ are the thermal expansion coefficient, the viscosity, and the density of the fluid, respectively, and g is the acceleration due to gravity, , are the components of the thermal diffusivity in x and y directions, respectively. The quantity qr in the right hand side of (2.4) represents the radiative heat flux in the y-direction. The radiative heat flux term is simplified by the Rosseland approximation (cf. [20]) and is taken as follows:
()
where σ and ω are the Stefan-Boltzmann constant and the mean absorption coefficient. The radiative heat flux in the x-direction is considered negligible in comparison with that in the y-direction [20]. The normal component of the velocity near the boundary is small compared with the other component of the velocity, and the derivatives of any quantity in the normal direction are large compared with derivatives of the quantity in direction of the wall. Under these assumptions, and by cross differentiation of (2.2) and (2.3) and subtracting, the above system of equations reduces to
()
()
()
Noting that the thermal diffusivity term is defined by , where λm is the effective thermal conductivity of the saturated porous medium. Likewise, α(y) also varies in the y-direction since it is related to the effective thermal conductivity of the saturated porous medium λm(y), which is defined as λm = λfε + (1 − ε)λs, where λf(y) and λs(y) are the thermal conductivity of the fluid and solid, respectively. Therefore, α(y) may be defined as
()
where, is the value of diffusivity at the edge of the boundary layer and σ* = λs/λf is the ratio of the thermal conductivity of the solid to the conductivity of the fluid. The term 16σ/3ω(ρ0CP) f can be considered as the radiative conductivity.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Schematic diagram of the problem.
Introducing the stream function, ψ, such that ru = ∂ψ/∂y and rv = −∂ψ/∂x, the continuity equation is automatically satisfied. Following Yih [10], we define the following transformations:
()
Moreover, it is assumed that u∞ = Bxm defines the velocity of the potential cone flow outside the boundary layer, where m = γ(π − γ) is the cone angle parameter, γ is half the cone angle, and B is constant. The tabulated values of γ and m are given by Hess and Faulkner [21]. The cone angle of 15, 30, 45, 60, and 750 are discussed in this paper, therefore, m is 0.0316314, 0.1156458, 0.2450773, 0.4241237, and 0.6667277, respectively. Furthermore, we choose such that K(y) and α(y)  are purely functions of η only. Substituting into (2.10) to (2.12), we obtain the following transformed governing equations:
()
()
where N = 1/β(TW − T∞), α*(η) = {ε0 + σ*(1 − ε0) + ε0ζ*e−η(1 − σ*)}, is the radiation parameter, and H = Tw/T∞ is the surface temperature parameter.
The boundary conditions become
()
The Darcian velocity components may be defined as
()
We note that χ = 0 and 1 correspond to pure free and forced convection cases, respectively. Between these limits, it represents combined free and forced convection cases. The heat flux qw at the surface of the cone is
()
For practical applications, it is usually the local Nusselt number that is of interest. This can be expressed as
()
where h denotes the local heat transfer coefficient and k represents the thermal conductivity. Substituting (2.6), and (2.19) into (2.20), we obtain
()
Primes in the above equations denote differentiation with respect to η, fχ = ∂f/∂χ and θχ = ∂θ/∂χ.

3. Results and Discussion

Numerical results for the governing (2.8)-(2.9) and the boundary conditions (2.10) are nonlinear partial differential equations depending on the mixed convection parameter χ, the radiation-condition parameter Rd, and the surface temperature parameter H for both UP and VP cases. Numerical results are presented for the mixed convection parameter χ ranging from 0 to 1.0, the cone angle parameter m ranging from 0.03163 to 0.66672, the radiation parameter Rd ranging from 0 to 1, and the surface temperature parameter H from 1.1 to 3.0 for both uniform permeability (UP), that is, d = d* = 0 and variable permeability (VP), that is, d, d* ≠ 0 cases. For the purpose of numerical integration we have assumed that d = 3, d* = 1.5 and ε0 = 0.4 (Christopher and Middleman [22]).

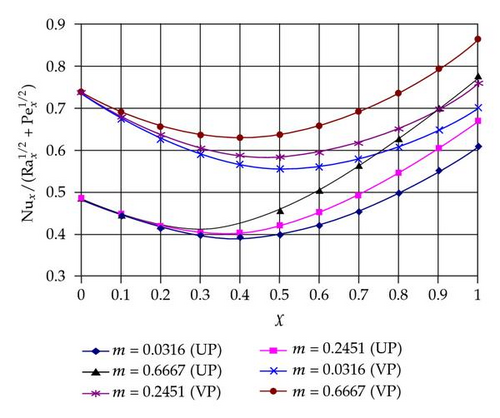
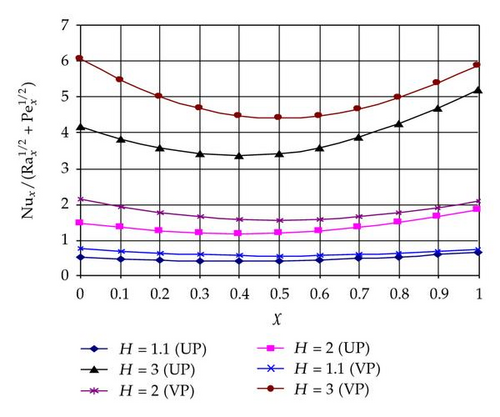
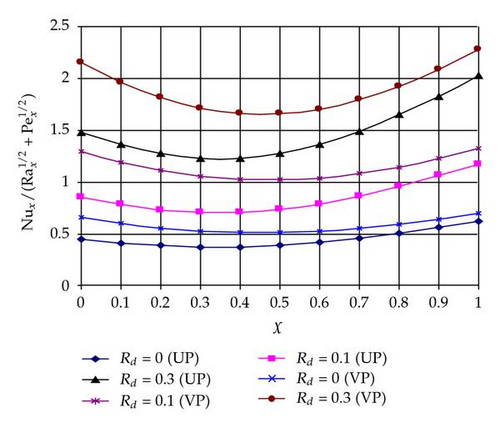
Figures 2–4 display results for the Nusselt number for various values of m, Rd,  χ and H for two cases UP and VP cases. From Figure 2, it is noteworthy that for pure free convection (χ = 0), there is no effect of the parameter m on the heat transfer rate on the surface, while for the pure forced convection (χ = 1), the parameter m enhances the heat transfer rate at the surface. It is observed from Figure 3 that the parameter H enhances the heat transfer rate, and Figure 4 shows that the parameter Rd enhances the heat transfer rate too. From Figures 2–4, it is interesting to note that the heat transfer rate at χ tends to 0 or 1 (i.e., at pure free and pure forced convection) and has the highest values.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Comparison of values for m and χ with Rd = 0.1 and H = 1.1 for both UP and VP cases.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Comparison of values for H and χ with m = 0.0316 and Rd = 0.3 for both UP and VP cases.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Comparison of values for R and χ with m = 0.2451 and H = 2.0 for both UP and VP cases.

Nomenclature

  • ar:
  • Rosseland mean extinction coefficient
  • B:
  • Constant
  • Cp:
  • Specific heat at constant pressure
  • d:
  • Constant defined in(2.5)
  • d*:
  • Constant defined in(2.5)
  • f:
  • Nondimensionless stream function
  • g:
  • Acceleration due to gravity
  • h:
  • Heat transfer coefficient
  • K(y):
  • Permeability of the porous medium
  • kr:
  • Thermal conductivity
  • K0:
  • Permeability at the edge of the boundary layer
  • m:
  • Cone angle parameter
  • Nux:
  • Local Nusselt number
  • Pex:
  • Local Peclet number
  • qr:
  • The rate of heat transfer
  • qw:
  • Surface heat flux
  • r:
  • Local radius of the cone
  • Rax:
  • Local Rayleigh number
  • Rd:
  • Radiation parameter
  • T:
  • Fluid temperature
  • Tw:
  • Wall temperature
  • T∞:
  • Free stream temperature
  • u, v:
  • Darcian velocity in the x and y directions
  • u∞:
  • Free stream velocity
  • x, y:
  • Coordinate axes along and perpendicular to the plate
  • α(y):
  • Thermal diffusivity
  • α*:
  • Ratio of viscosities
  • α0:
  • Thermal diffusivity at the edge of the boundary layer
  • β:
  • Volumetric coefficient of thermal expansion
  • γ:
  • Half angle of the cone
  • ε(y):
  • Porosity of the saturated porous medium
  • ε0:
  • Porosity at the edge of the boundary layer
  • η:
  • Dimensionless distance
  • θ:
  • Dimensionless temperature
  • λ:
  • Constant in(2.2)
  • λm:
  • Effective thermal conductivity of the porous medium
  • μ:
  • Viscosity of porous medium
  • ν:
  • Kinematics viscosity of the fluid
  • ψ:
  • Stream function
  • ρ:
  • Density of fluid
  • χ:
  • Mixed convection parameter
  • σ*:
  • Ratio of thermal conductivity of the solid to the liquid
  • σ:
  • Permeability parameter

    • Subscripts

  • w:
  • Surface conditions
  • ∞:
  • Condition far away from surface.

      • The full text of this article hosted at iucr.org is unavailable due to technical difficulties.