A new iterative technique is employed to solve a system of nonlinear fractional partial differential equations. This new approach requires neither Lagrange multiplier like variational iteration method (VIM) nor polynomials like Adomian′s decomposition method (ADM) so that can be more easily and effectively established for solving nonlinear fractional differential equations, and will overcome the limitations of these methods. The obtained numerical results show good agreement with those of analytical solutions. The fractional derivatives are described in Caputo sense.

1. Introduction

In recent years, it has been turned out that fractional differential equations can be used successfully to model many phenomena in various fields such as fluid mechanics, viscoelasticity, physics, chemistry, and engineering. For instance, the fluid−dynamics traffic model with fractional derivatives [1] is able to eliminate the deficiency arising from the assumption of continuum traffic flow, and the nonlinear oscillation of earthquakes can be modeled by fractional derivatives [2]. Fractional differentiation and integration operators can also be used for extending the diffusion and wave equations [3]. Most of fractional differential equations do not have exact analytical solutions, hence considerable heed has been focused on the approximate and numerical solutions of these equations. Although variational iteration method [4−8] and Adomian’s decomposition method [9−14] are approaches that have been utilized extensively to provide analytical approximations of linear and nonlinear problems, they have limitations due to complicated algorithms of calculating Adomian polynomials for nonlinear fractional problems, and an inherent inaccuracy in determining the Lagrange multiplier for fractional equations. In this study, a new alternative procedure that needs no Lagrange multiplier or Adomian polynomials is used to obtain an analytical approximate solution of a system of nonlinear fractional partial differential equations (1.1) to illustrate the effectiveness, accuracy, and convenience of this method.

In this work, we consider the solution of generalized Hirota−Satsuma coupled KdV of time−fractional order which is presented by a system of nonlinear partial differential equations, of the form:

()

subject to the following initial conditions:

()

where k, c₀, c₁ ≠ 0, and β are arbitrary constants. The Hirota−Satsuma system of equations [15] was introduced to describe the interaction of two long waves with different dispersion relations. The case of α = 1 in system (1.1) was solved by Wu et al. [16]. If c = −β, then in one case the u(x, t) = ((β − 2k²)/3) + 2k²tanh²(k(x − ct)),

and w(x, t) = c₀ + c₁tanh(k(x − ct)) are travelling−wave solutions of system (1.1) when α = 1.

2. Basic Definitions

In this section, there are some basic definitions and properties of the fractional calculus theory which are used in this paper.

Definition 2.1. A real function f(x), x > 0, is mentioned to be in the space C_μ, μ ∈ R if there exists a real number p(>μ) such that f(x) = x^pf₁(x), where f₁(x) ∈ C[0, ∞), and it is said to be in the space if f^(m) ∈ C_μ, m ∈ N.

Definition 2.2. The left−sided Riemann−Liouville fractional integral operator of order α ≥ 0, of a function f ∈ C_μ, μ ≥ −1 is defined as

()

The properties of the operator D^−α can be found in [1, 17], and we only mention the following (in this case, f ∈ C_μ, μ ≥ −1, α, β ≥ 0 and γ > −1):

()

The Riemann−Liouville derivative has certain disadvantages, in trying way to model real−world phenomena with fractional differential equations. Therefore, we will employ a modification of fractional differential operator proposed by Caputo, in his work [18] on the theory of viscoelasticity.

Definition 2.3. The (left−sided) Caputo fractional derivative of f(x) is defined as

()

for

Also, we need two of its basic properties.

Lemma 2.4. If m − 1 < α ≤ m, m ∈ N, and , then one has:

()

The Caputo fractional derivative is considered here, because it allows traditional initial and boundary conditions to be included in the formulation of the problem.

In this work, we consider the one−dimensional linear nonhomogeneous fractional partial differential equations in fluid mechanics, where the unknown function u(x, t) is assumed to be a causal function of time, that is, vanishing for t < 0.

Definition 2.5. For m as the smallest integer that exceeds α, the Caputo time−fractional derivative operator of order α > 0 is defined as

()

For more information on the mathematical properties of fractional derivatives and integrals, one can consult the mentioned references.

3. Basic Ideas of Fractional Iteration Method (FIM)

As pointed in [19], to illustrate fractional iteration method, we consider the following nonlinear fractional differential equation (more general form can be considered without loss of generality):

()

where the fractional differential operator

is deﬁned as in (2.3), m − 1 < α ≤ m, m ∈ N, f is a nonlinear function of y, and y is an unknown function to be determined later. We want to find a solution y of (3.1) having the form

()

Let H(x) ≠ 0 denote the so−called auxiliary function. Multiplying (3.1) by H(x) and then applying , the Riemann−Liouville fractional integral operator, of order γ ≥ 0 defined by (2.1), on both sides of the resulted term yields

()

Let h ≠ 0 denote the so−called auxiliary parameter. Multiplying (3.3) by h and then adding y, the solution of (3.1), on both sides of the resulted term yields

()

However (3.4) can be solved iteratively as follows:

()

In (3.5), the subscript n denotes the nth iteration, and provided that the right hand of it, that is, , is a contractive mapping. The convergence of (3.5) is ensured by Banach’s fixed point theorem [20], as is shown in [19].

Now, we introduce a new convenient technique for controlling the convergence region and rate of solution series for this method. Assume that we gain a family of solution series in the auxiliary parameter h by the means of fractional iteration method. Like HAM, by plotting the amount of the function or one of its derivatives at a particular point with respect to the auxiliary parameter h (which is the so−called h −curve), we can obtain a proper value of h that ensures the convergence of the solution series. This proper value of h corresponds to the curve segment nearly parallel to the horizontal axis in the h −curve plot. Therefore, if we set h any value in this region, which is so−called the valid region of h, we are quite sure that the corresponding solution series converge.

Having freedom for choosing the auxiliary function H(x), the auxiliary parameter h, the initial approximation y₀(x), and the fractional integral order γ, that is, fundamental to the validity and flexibility of the FIM, we can suppose that all of them are properly chosen, therefore, the iterative scheme (3.5) will converge to the exact solution. Accordingly, the successive approximations y_n(x), n ≥ 0, of the solution y(x) will be obtained by choosing y₀(x) that at least satisﬁes the initial and/or boundary conditions. Consequently, the exact solution may be obtained by using y(x) = lim _n→∞y_n(x).

4. Applications

In this section, we implement fractional iteration method to generalized Hirota−Satsuma coupled KdV of time−fractional order when 0 < α ≤ 1. For convenience in applying FIM method, we choose the initial conditions given in (1.2) as the initial approximations:

()

Choosing γ = α and H(x, t) = 1, we can construct the iterative scheme (3.5) for investigation of the traveling wave solution of (1.1) as follows:

()

Substituting the initial approximations, (4.1), into (4.2), for the case α = 1, yields

()

5. Result and Discussion

In this section, four figures are presented corresponding to FIM results and exact solutions for the solitary wave solutions u(x, t), v(x, t), and w(x, t) with the initial conditions (1.2), when k = 0.1, α = 1, β = 1.5, c₀ = 1.5, c₁ = 0.1. Furthermore, numerical values for the case α = 0.5, 0.75, 1.0, and k = 0.1, β = 1.5, c₀ = 1.5, c₁ = 0.1 are obtained for u(x, t), v(x, t), and w(x, t).

Demonstrating the exactness of FIM, the numerical results are presented and only few iterations are required to achieve accurate solutions. The convergence of FIM for the generalized fractional−order Hirota−Satsuma−coupled KdV equation is controllable, using the so−called h −curves presented in Figure 1 which are obtained based on the fourth−order FIM approximate solutions. In general, by the means of the so−called h −curve, it is straight forward to choose a proper value of h which ensures that the solution series is convergent. This proper value of h corresponds to the curve segment nearly parallel to the horizontal axis. Both exact results and approximate solutions obtained for the first four approximations are plotted in Figures 2, 3, and 4. There are no visible differences in two solutions of each pair of diagrams.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

h−curves of u(x, t): dash, v(x, t): dash dot, and w(x, t): solid when k = 0.1, α = 1, β = 1.5, c₀ = 1.5, c₁ = 0.1 at point (1,0.6).

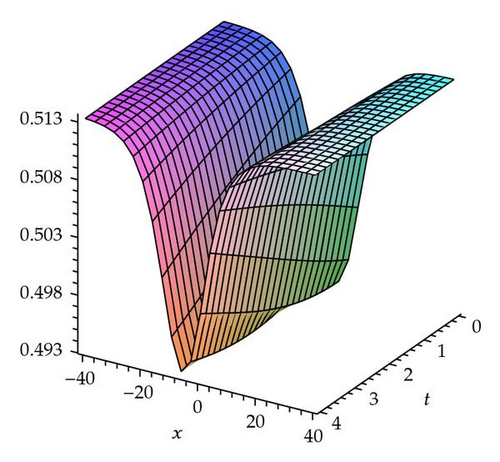
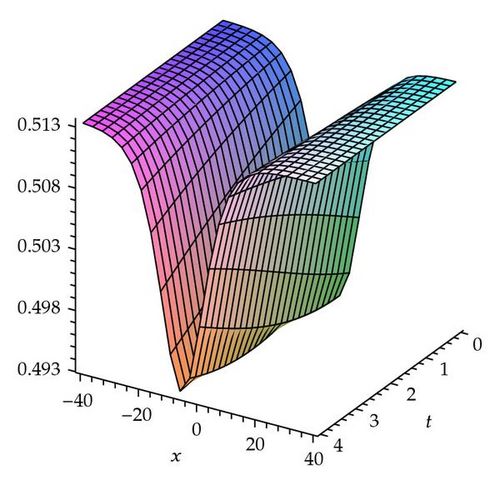
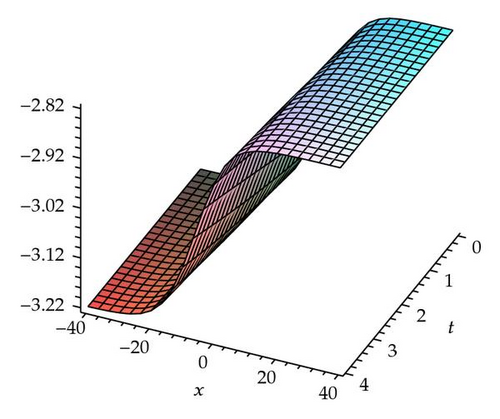
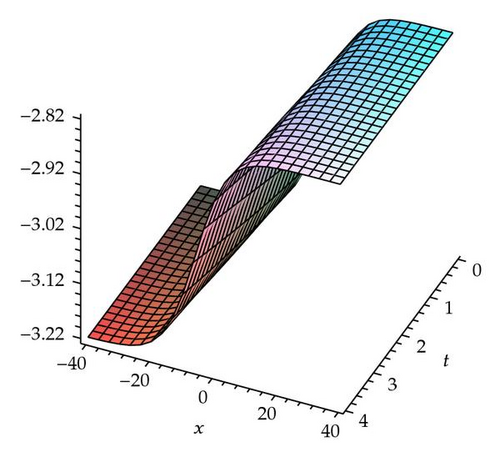
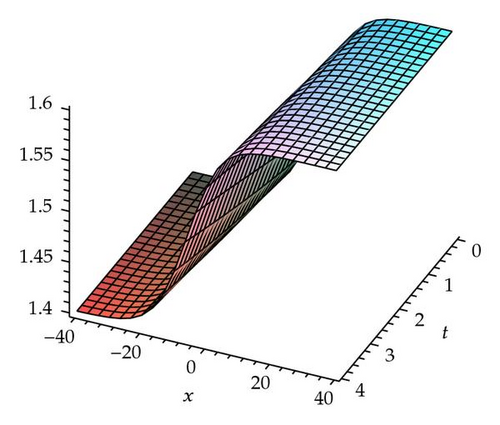
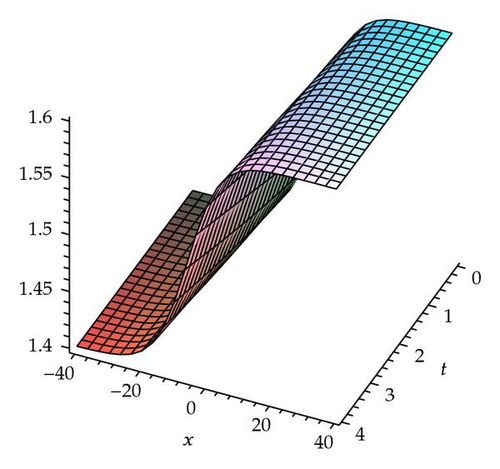
Tables 1, 2, and 3 show the numerical values by FIM when α = 0.5, 0.75, 1.0 and k = 0.1, β = 1.5, c₀ = 1.5, c₁ = 0.1 for u(x, t), v(x, t), and w(x, t) respectively.

Table 1. Numerical values when α = 0.5, 0.75, 1.0 and k = 0.1, β = 1.5, c₀ = 1.5, c₁ = 0.1 for u(x, t).

t	x	α = 0.5		α = 0.75		α = 1.0
t	x	u_FIM	u_HPM	u_FIM	u_HPM	u_FIM	u_HPM	u_Exact
0.2	0	0.4935113355	0.4933513333	0.4933937249	0.4933513333	0.4933513226	0.4933513333	0.4933513225
	0.25	0.4935979177	0.4934136490	0.4934546200	0.4934060408	0.4933937118	0.4933937581	0.4933937115
	0.5	0.4937081918	0.4935005536	0.4935399023	0.4934853752	0.4934607890	0.4934608711	0.4934607891
	0.75	0.4938416235	0.4936116158	0.4936491516	0.4935889426	0.4935522228	0.4935523392	0.4935522227
	1	0.4939975728	0.4937462882	0.4937818335	0.4937162326	0.4936675611	0.4936677111	0.4936675613

0.4	0	0.4936853330	0.4934053333	0.4935033001	0.4934053333	0.4934051602	0.4934053333	0.4934051609
	0.25	0.4938008948	0.4935090262	0.4935963610	0.4934954686	0.4934771397	0.4934775983	0.4934771401
	0.5	0.4939391903	0.4936368323	0.4937131147	0.4936097847	0.4935733947	0.4935741334	0.4935733945
	0.75	0.4940995646	0.4937881198	0.4938529939	0.4937477171	0.4936934501	0.4936944620	0.4936934499
	1	0.4942812668	0.4939621476	0.4940153259	0.4939085897	0.4938367205	0.4938379949	0.4938367203

0.6	0	0.4938553137	0.4934953333	0.4936435681	0.4934953333	0.4934944586	0.4934953333	0.4934944625
	0.25	0.4939921388	0.4936348749	0.4937639292	0.4936174202	0.4935955155	0.4935973485	0.4935955186
	0.5	0.4941508292	0.4937979026	0.4939071763	0.4937630802	0.4937202663	0.4937230371	0.4937202675
	0.75	0.4943306471	0.4939836133	0.4940726248	0.4939315968	0.4938681006	0.4938717813	0.4938681010
	1	0.4945307679	0.4941911034	0.4942594934	0.4941221502	0.4940383061	0.4940428589	0.4940383061

Table 2. Numerical values when α = 0.5, 0.75, 1.0 and k = 0.1, β = 1.5, c₀ = 1.5, c₁ = 0.1 for v(x, t).

t	x	α = 0.5		α = 0.75		α = 1.0
t	x	v_FIM	v_HPM	v_FIM	v_HPM	v_FIM	v_HPM	v_Exact
0.2	0	−3.004851885	−3.009951963	−3.010186962	−3.011485031	−3.013961813	−3.013960000	−3.013961811
	0.25	−2.999873282	−3.004930481	−3.005175951	−3.006462592	−3.008937820	−3.008936014	−3.008937819
	0.5	−2.994919279	−2.999927784	−3.000183326	−3.001457026	−3.003927607	−3.003925818	−3.003927606
	0.75	−2.989995777	−2.994950010	−2.995215173	−2.996474487	−2.998937350	−2.998935586	−2.998937348
	1	−2.985108534	−2.990003168	−2.990277460	−2.991521007	−2.993973118	−2.993971391	−2.993973120

0.4	0	−2.998707345	−3.001587258	−3.003540427	−3.004319121	−3.007934500	−3.007920000	−3.007934475
	0.25	−2.993774914	−2.996584581	−2.998560913	−2.999314737	−3.002927784	−3.002913367	−3.002927763
	0.5	−2.988873896	−2.991611047	−2.993607731	−2.994336092	−2.997942249	−2.997927984	−2.997942228
	0.75	−2.984009951	−2.986672646	−2.988686777	−2.989389199	−2.992983946	−2.992969899	−2.992983924
	1	−2.979188572	−2.981775197	−2.983803790	−2.984479922	−2.988058789	−2.988045031	−2.988058768

0.6	0	−2.994081735	−2.994318388	−2.997767879	−2.997835535	−3.001928965	−3.001880000	−3.001928766
	0.25	−2.989192682	−2.989342884	−2.992826759	−2.992857834	−2.996948389	−2.996899772	−2.996948197
	0.5	−2.984339775	−2.984405468	−2.987918608	−2.987913837	−2.991996239	−2.991948208	−2.991996054
	0.75	−2.979528475	−2.979511953	−2.983049116	−2.983009390	−2.987078404	−2.987031190	−2.987078224
	1	−2.974764060	−2.974667936	−2.978223778	−2.978150144	−2.982200600	−2.982154433	−2.982200431

Table 3. Numerical values when α = 0.5, 0.75, 1.0 and k = 0.1, β = 1.5, c₀ = 1.5, c₁ = 0.1 for w(x, t).

t	x	α = 0.5		α = 0.75		α = 1.0
t	x	w_FIM	w_HPM	w_FIM	w_HPM	w_FIM	w_HPM	w_Exact
0.2	0	1.507523900	1.504990747	1.504874024	1.504229289	1.502999100	1.503000000	1.502999100
	0.25	1.509996714	1.507484860	1.507362938	1.506723878	1.505494461	1.505495357	1.505494461
	0.5	1.512457311	1.509969643	1.509842719	1.509210085	1.507982979	1.507983864	1.507982977
	0.75	1.514902760	1.512442049	1.512310343	1.511684858	1.510461580	1.510462458	1.510461582
	1	1.517330199	1.514899088	1.514762850	1.514145194	1.512927259	1.512928117	1.512927258

0.4	0	1.510575823	1.509145401	1.508175285	1.507788516	1.505992798	1.506000000	1.505992810
	0.25	1.513025704	1.511630175	1.510648553	1.510274137	1.508479570	1.508486739	1.508479588
	0.5	1.515459985	1.514100473	1.513108742	1.512746974	1.510955834	1.510962922	1.510955847
	0.75	1.517875852	1.516553321	1.515552926	1.515204040	1.513418571	1.513425547	1.513418581
	1	1.520270576	1.518985828	1.517978251	1.517642422	1.515864843	1.515871673	1.515864850

0.6	0	1.512873311	1.512755768	1.511042443	1.511008840	1.508975680	1.509000000	1.508975778
	0.25	1.515301647	1.515227046	1.513496642	1.513481209	1.511449479	1.511473624	1.511449571
	0.5	1.517712032	1.517679404	1.515934464	1.515936836	1.513909155	1.513933009	1.513909245
	0.75	1.520101750	1.520109958	1.518353088	1.518372820	1.516351785	1.516375237	1.516351875
	1	1.522468182	1.522515926	1.520749779	1.520786351	1.518774537	1.518797467	1.518774621

6. Conclusion

In this paper, the fractional iteration method (FIM) has been successfully applied to study Hirota−Satsuma−coupled KdV of time−fractional−order equation. FIM results are compared with the exact solutions and those obtained by Homotopy perturbation method [21].

The results show that fractional iteration method is a powerful and efficient technique in finding exact and approximate solutions for nonlinear partial differential equations of fractional order. The method provides the user with more realistic series solutions that converge very rapidly in real physical problems.

Compared with the ADM and VIM, the FIM has following advantages, [19].

(1)
The auxiliary parameter h provides us with a convenient way to modify and control the convergence region of the solution.
(2)
The solution of a given nonlinear problem can be expressed by an infinite number of solution series and thus can be more efficiently approximated by a better selection of the auxiliary parameter values.
(3)
Unlike the ADM, the FIM method is free from the need to use Adomian polynomials.
(4)
This method has no need for the Lagrange multiplier, correction functional, stationary conditions, the variational theory, and so forth, which eliminates the complications that exist in the VIM.
(5)
The fractional iteration method can be easily comprehended with only a basic knowledge of fractional calculus.
(6)
Compared to the ADM and VIM, the presented method proves simpler in its principles and more convenient for computer algorithms.

In this work, we used Maple Package to calculate the series obtained by fractional iteration method.

References

1 Podlubny I., Fractional Differential Equations, 1999, Academic Press, New York, NY, USA.
Web of Science® Google Scholar
2 Mainardi F., Fractional Calculus Some Basic Problems in Continuum and Statistical Mechanics, 1997, Springer, New York, NY, USA.
Google Scholar
3 Schneider W. R. and Wyss W., Fractional diffusion and wave equations, Journal of Mathematical Physics. (1989) 30, 134–144.
10.1063/1.528578
Web of Science® Google Scholar
4 He J. H., Approximate analytical solution for seepage flow with fractional derivatives in porous media, Computer Methods in Applied Mechanics and Engineering. (1998) 167, 57–68.
10.1016/S0045-7825(98)00108-X
Web of Science® Google Scholar
5 He J. H., Variational iteration method—some recent results and new interpretations, Journal of Computational and Applied Mathematics. (2007) 207, no. 1, 3–17, https://doi.org/10.1016/j.cam.2006.07.009.
10.1016/j.cam.2006.07.009
Web of Science® Google Scholar
6 He J. H. and Wu X. H., Variational iteration method: new development and applications, Computers and Mathematics with Applications. (2007) 54, no. 7-8, 881–894, https://doi.org/10.1016/j.camwa.2006.12.083.
10.1016/j.camwa.2006.12.083
Web of Science® Google Scholar
7 Tari H., [email protected], Ganji D. D., and [email protected], Babazadeh H., [email protected], The application of He′s variational iteration method to nonlinear equations arising in heat transfer, Physics Letters, Section A. (2007) 363, no. 3, 213–217, https://doi.org/10.1016/j.physleta.2006.11.005.
10.1016/j.physleta.2006.11.005
CAS Web of Science® Google Scholar
8 Abbasbandy S. and Shirzadi A., The variational iteration method for a family of fifth-order boundary value differential equations, International Journal of Nonlinear Dynamics in Engineering and Sciences. (2009) 1, no. 1, 39–46.
Google Scholar
9 Adomian G., Solving Frontier Problems of Physics: The Decomposition Method, 1994, Kluwer Academic Publishers, Boston, Mass, USA.
10.1007/978-94-015-8289-6
Google Scholar
10 Adomian G., A review of the decomposition method in applied mathematics, Journal of Mathematical Analysis and Applications. (1988) 135, no. 2, 501–544.
10.1016/0022-247X(88)90170-9
Web of Science® Google Scholar
11 Adomian G., Solutions of nonlinear P.D.E, Applied Mathematics Letters. (1998) 11, no. 3, 121–123.
10.1016/S0893-9659(98)00043-3
Web of Science® Google Scholar
12 Esmaili Q., Ramiar A., Alizadeh E., and Ganji D. D., [email protected], An approximation of the analytical solution of the Jeffery-Hamel flow by decomposition method, Physics Letters A. (2008) 372, no. 19, 3434–3439, https://doi.org/10.1016/j.physleta.2008.02.006.
10.1016/j.physleta.2008.02.006
CAS Web of Science® Google Scholar
13 Wazwaz A. M., A new algorithm for calculating adomian polynomials for nonlinear operators, Applied Mathematics and Computation. (2000) 111, no. 1, 53–69.
10.1016/S0096-3003(99)00063-6
Web of Science® Google Scholar
14 Momani S. and [email protected], Odibat Z., [email protected], Analytical solution of a time-fractional Navier-Stokes equation by Adomian decomposition method, Applied Mathematics and Computation. (2006) 177, 488–494, https://doi.org/10.1016/j.amc.2005.11.025.
10.1016/j.amc.2005.11.025
Web of Science® Google Scholar
15 Hirota R. and Satsuma J., Soliton solutions of a coupled Korteweg-de Vries equation, Physics Letters A. (1981) 85, no. 8-9, 407–408.
10.1016/0375-9601(81)90423-0
Web of Science® Google Scholar
16 Wu Y., Geng X., Hu X., and Zhu S., A generalized Hirota-Satsuma coupled Korteweg-de vries equation and Miura transformations, Physics Letters A. (1999) 255, 259–264.
10.1016/S0375-9601(99)00163-2
CAS Web of Science® Google Scholar
17 Podlubny I., S. Elaydi, I. Gyori, and G. Ladas, Numerical solution of ordinary fractional differential equations by the fractional difference method, Advances in Difference Equations, 1997, Gordon and Breach, Amsterdam, The Netherlands.
Google Scholar
18 Caputo M., Linear models of dissipation whose Q is almost frequency independent, Journal of the Royal Astronomical Society. (1967) 13, 529–539.
10.1111/j.1365-246X.1967.tb02303.x
Web of Science® Google Scholar
19 Ghorbani A., [email protected], Toward a new analytical method for solving nonlinear fractional differential equations, Computer Methods in Applied Mechanics and Engineering. (2008) 197, 4173–4179, https://doi.org/10.1016/j.cma.2008.04.015.
10.1016/j.cma.2008.04.015
Web of Science® Google Scholar
20 Reed M. and Simon B., Methods of Modern Mathematical Physics, I: Functional Analysis, 1980, Academic Press, New York, NY, USA.
Google Scholar
21 Ganji Z. Z., Ganji D. D., and Rostamiyan Y., Solitary wave solutions for a time-fraction generalized Hirota-Satsuma coupled KdV equation by an analytical technique, Applied Mathematical Modelling. (2009) 33, no. 7, 3107–3113, https://doi.org/10.1016/j.apm.2008.10.034, EID2-s2.0-61449224678.
10.1016/j.apm.2008.10.034
Web of Science® Google Scholar

Citing Literature

All articles

Solitary Wave Solutions for a Time-Fraction Generalized Hirota-Satsuma Coupled KdV Equation by a New Analytical Technique

Abstract

1. Introduction

2. Basic Definitions

3. Basic Ideas of Fractional Iteration Method (FIM)

4. Applications

5. Result and Discussion

6. Conclusion

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Solitary Wave Solutions for a Time-Fraction Generalized Hirota-Satsuma Coupled KdV Equation by a New Analytical Technique

Abstract

1. Introduction

2. Basic Definitions

3. Basic Ideas of Fractional Iteration Method (FIM)

4. Applications

5. Result and Discussion

6. Conclusion

References

Citing Literature

Figures

References

Related

Information