Sign-Changing Solutions for Nonlinear Elliptic Problems Depending on Parameters
Abstract
The study of multiple solutions for quasilinear elliptic problems under Dirichlet or nonlinear Neumann type boundary conditions has received much attention over the last decades. The main goal of this paper is to present multiple solutions results for elliptic inclusions of Clarke′s gradient type under Dirichlet boundary condition involving the p-Laplacian which, in general, depend on two parameters. Assuming different structure and smoothness assumptions on the nonlinearities generating the multivalued term, we prove the existence of multiple constant-sign and sign-changing (nodal) solutions for parameters specified in terms of the Fučik spectrum of the p-Laplacian. Our approach will be based on truncation techniques and comparison principles (sub-supersolution method) for elliptic inclusions combined with variational and topological arguments for, in general, nonsmooth functionals, such as, critical point theory, Mountain Pass Theorem, Second Deformation Lemma, and the variational characterization of the “beginning”of the Fu\v cik spectrum of the p-Laplacian. In particular, the existence of extremal constant-sign solutions and their variational characterization as global (resp., local) minima of the associated energy functional will play a key-role in the proof of sign-changing solutions.
1. Introduction
The existence of multiple solutions for semilinear and quasilinear elliptic problems has been studied by a number of authors, for example, [10–24]. All these papers deal with nonlinearities (x, s) ↦ g(x, s) that are sufficiently smooth.
2. Problem (1.4) for λ being Small
The aim of this section is to provide an existence result of multiple solutions for all values of the parameter λ in an interval (0, λ0), with λ0 > 0, guaranteeing that for any such λ there exist at least three nontrivial solutions of problem (1.4), two of them having opposite constant sign and the third one being sign-changing (or nodal). More precisely, we demonstrate that under suitable assumptions there exist a smallest positive solution, a greatest negative solution, and a sign-changing solution between them, whereas the notions smallest and greatest refer to the underlying natural partial ordering of functions. This continues the works of Jin [25] (where p = 2 and f(x, s, λ) is Hölder continuous with respect to for every fixed λ) and of Motreanu-Motreanu-Papageogiou [26]. In these cited works one obtains three nontrivial solutions, two of which being of opposite constant sign, but without knowing that the third one changes sign. Here we derive the new information of having, in addition, a sign-changing solution by strengthening the unilateral condition for the right-hand side of the equation in (1.4) at zero. Furthermore, under additional hypotheses, we demonstrate that one can obtain two sign-changing solutions.
2.1. Hypotheses and Example
-
H(f) , with , is a function such that f(x, 0, λ) = 0 for a.a. x ∈ Ω, whenever , and one has the following.
- (i)
For all , f(·, ·, λ) is Carathéodory (i.e., f(·, s, λ) is measurable for all s ∈ ℝ and f(x, ·, λ) is continuous for almost all x ∈ Ω).
- (ii)
There are constants c > 0, r > p − 1, and functions a(·, λ) ∈ L∞(Ω) + () with ∥a(·, λ)∥∞ → 0 as λ ↓ 0 such that
(2.2) - (iii)
For all there exist constants μ0 = μ0(λ) > λ2, ν0 = ν0(λ) > μ0 and a set Ωλ ⊂ Ω with Ω∖Ωλ of Lebesgue measure zero such that
(2.3)uniformly with respect to x ∈ Ωλ.
In H(f)(iii), λ2 denotes the second eigenvalue of (−Δp, V0). As mentioned in the Introduction, the strengthening with respect to [26] (see also [25]) of the unilateral condition for the right-hand side f in (1.4), which enables us to obtain, in addition, sign-changing solutions, consists in adding the part involving the limit superior in H(f)(iii).
Let us provide an example where all the assumptions formulated in H(f) are fulfilled.
Example 2.1. For the sake of simplicity we drop the x dependence for the function f in the right-hand side of (1.4). The function f : ℝ × (0, +∞) → ℝ given by
2.2. Constant-Sign Solutions
Lemma 2.2. Let the data c, r, and a(·, λ) be as in H(f)(ii). Then for every constant θ > 0 there is with the property that if λ ∈ (0, λ0), one can choose ξ0 = ξ0(λ)∈(0, θ) such that
Proof. On the contrary there would exist a constant θ > 0 and a sequence λn ↓ 0 as n → ∞ such that
Lemma 2.3. Assume H(f)(i) and (ii) and the following weaker form of hypothesis H(f)(iii): for all there exist μ0 = μ0(λ) > λ1 and Ωλ ⊂ Ω with Ω∖Ωλ of Lebesgue measure zero such that
Fix a constant θ > 0 and consider the corresponding number obtained in Lemma 2.2. Then for any λ ∈ (0, λ0) the function , with ξ0 ∈ (0, θ) given by Lemma 2.2, is a supersolution for problem (1.4), and the function is a subsolution of problem (1.4) provided that the number ε > 0 is sufficiently small.
Proof. For a fixed λ ∈ (0, λ0), from (2.9) and H(f)(ii) we derive
On the other hand, by hypothesis we can find μ = μ(λ) > λ1 and δ = δ(λ) > 0 such that
The following result which asserts the existence of two solutions of problem (1.4) having opposite constant sign and being extremal plays an important role in the proof of the existence of sign-changing solutions.
Theorem 2.4. Assume H(f)(i) and (ii) and the following weaker form of H(f)(iii): for all there exist constants μ0 = μ0(λ) > λ1, ν0 = ν0(λ) > μ0 and a set Ωλ ⊂ Ω with Ω∖Ωλ of Lebesgue measure zero such that
Proof. Since the proof of the existence of the greatest negative solution follows the same lines, we only provide the arguments for the existence of the least positive solution.
Applying Lemma 2.3 for θ = b/∥e∥∞ we find as therein. Fix λ ∈ (0, λ0). Lemma 2.3 ensures that is a supersolution for problem (1.4), with ξ0 ∈ (0, b/∥e∥∞) given by Lemma 2.2, and is a subsolution for problem (1.4) if ε > 0 is small enough. Passing eventually to a smaller ε > 0, we may assume that εφ1 ≤ ξ0e. Then by the method of sub-supersolution we know that in the order interval [εφ1, ξ0e] there is a least (i.e., smallest) solution of problem (1.4) (see [29]).
We thus obtain that for every positive integer n sufficiently large there is a least solution of problem (1.4) in the order interval [(1/n)φ1, ξ0e]. Clearly, we have
By (2.18) and the nonlinear regularity theory (cf., e.g., Theorem 1.5.6 in [27]) it turns out . The choice of ξ0 guarantees that
We claim that
In view of (2.18) it remains to establish that u+ is the smallest positive solution of problem (1.4) in the interval . Let u ∈ V0 be a positive solution to (1.4) in . Since u ∈ L∞(Ω), then (1.4) and H(f)(ii) allow to deduce that −Δpu ∈ L∞(Ω). Using Theorem 1.5.6 of [27] leads to . Then, as u is a solution to (1.4) and , with , by means of hypotheses H(f)(ii) and (iii), we are able to apply the strong maximum principle. So we get , hence for n sufficiently large. The fact that un is the least solution of (1.4) in ensures un ≤ u. Taking into account (2.17), we obtain u+ ≤ u. This completes the proof.
2.3. Sign-Changing Solution
The main result of this section is as follows.
Theorem 2.5. Under hypotheses H(f), for all b > 0, there exists a number with the property that if λ ∈ (0, λ0), then problem (1.4) has a (positive) solution , a (negative) solution and a nontrivial sign-changing solution satisfying ∥u+∥∞ < b, ∥u−∥∞ < b, ∥u0∥∞ < b.
Proof. Let b > 0. Consider the positive number λ0 given by Theorem 2.4 and fix λ ∈ (0, λ0). Let and be the two extremal solutions determined in Theorem 2.4. We introduce on Ω × ℝ the truncation functions
We observe that if v is a critical point of E+, then
Since the function E+ is coercive and weakly lower semicontinuous, there exists a global minimizer z+ ∈ V0 of it. Using (2.14), it is seen that
Since , there exists a neighborhood 𝒰 of u+ in the space such that . Therefore E0 = E+ on 𝒰, which guarantees that u+ is a local minimizer of E0 on . It results that u+ is also a local minimizer of E0 on the space V0 (see [27], pages 655-656 ). Employing the functional E− and proceeding as in the case of u+, we establish that u− is a local minimizer of E0 on V0.
As in the case of (2.55), we verify that every critical point of E0 belongs to the set {u ∈ V0 : u−(x) ≤ u(x) ≤ u+(x) a.e. x ∈ Ω}, which implies that every critical point of E0 is a solution to problem (1.4). The functional E0 is coercive, weakly lower semicontinuous, with . Thus E0 has a global minimizer y0 ∈ V0 with y0 ≠ 0. The above properties ensure that y0 is a nontrivial solution of problem (1.4) belonging to the order interval [u−, u+]. Assume y0 ≠ u+ and y0 ≠ u−. We claim that y0 changes sign. Indeed, if not, y0 would have constant sign, for instance y0 ≥ 0 a.e. on Ω. Using assumptions H(f)(ii) and (iii) and the boundedness of y0, we may apply the strong maximum principle which leads to y0 > 0 on Ω. This is impossible because it contradicts the minimality property of the solution u+ as given by Theorem 2.4. According to the claim, we obtain the conclusion of the theorem setting u0 = y0.
Thus, the proof reduces to consider the cases y0 = u+ or y0 = u−. To make a choice, suppose y0 = u+. We may also admit that u− is a strict local minimizer of E0. This is true since on the contrary we would find (infinitely many) critical points x0 of E0 belonging to the order interval [u−, u+] which are different from 0, u−, u+, and if x0 does not change sign, taking into account the strong maximum principle, the extremality properties of the solutions u−, u+ given in Theorem 2.4 will be contradicted. A straightforward argument allows then to find ρ ∈ (0, ∥u+ − u−∥) such that
The next step in the proof is to show that
At this point we apply the second deformation lemma (see, e.g., [27, page 366]) to the C1 functional E+ : V0 → ℝ. Towards this let us denote
2.4. Two Sign-Changing Solutions
The goal of this section is to show that under hypotheses stronger than those in Theorem 2.5, problem (1.4) possesses at least two sign-changing solutions.
-
H′(f) , with , is a function such that f(x, 0, λ) = 0 for a.a. x ∈ Ω, whenever .
- (i)
For all , .
- (ii)
There are constants c > 0, r ∈ (p − 1, p* − 1), and functions a(·, λ) ∈ L∞(Ω) + () with ∥a(·,λ)∥∞ → 0 as λ ↓ 0 such that
(2.76) - (iii)
For all there exist constants μ0 = μ0(λ) > λ2, ν0 = ν0(λ) > μ0 and a set Ωλ ⊂ Ω with Ω∖Ωλ of Lebesgue measure zero such that
(2.77)uniformly with respect to x ∈ Ωλ. - (iv)
There exist constants b− < 0 < b+ such that for all we have
(2.78) - (v)
For every , there exist M = M(λ) > 0 and μ = μ(λ) > p such that
We notice that hypotheses H'(f) are stronger than H(f). In particular, for every , we added the Ambrosetti-Rabinowitz condition for f(·, ·, λ) (see hypothesis H'(f)(v)).
We state now the main result of this section, which produces two sign-changing solutions for problem (1.4).
Theorem 2.6. Assume that hypotheses H'(f) are fulfilled. Then there exists a number with the property that if λ ∈ (0, λ0), then problem (1.4) has a minimal (positive) solution , a maximal (negative) solution and two nontrivial sign-changing solutions satisfying ∥u+∥∞ < b, ∥u−∥∞ < b, u− ≤ u0 ≤ u+ a.e. in Ω (so ∥u0∥∞ < b) and ∥w0∥∞ ≥ b, where b : = min {b+, |b−|}.
Proof. Since hypotheses H'(f) are stronger than H(f), we can apply Theorem 2.5 with b = min {b+, |b−|}, which ensures the existence of a number such that for every λ ∈ (0, λ0), problem (1.4) possesses a positive solution , a negative solution and a sign-changing solution with −b < u− ≤ u0 ≤ u+ < b. The proof of Theorem 2.5 shows that u+ and u− can be chosen to be the minimal positive solution and the maximal negative solution, respectively.
On the other hand, hypotheses H'(f) enable us to apply Theorem 1.1 of Bartsch et al. [33]. It follows that there exists a sign-changing solution (by the nonlinear regularity theory) with and . Therefore, we have ∥w0∥∞ ≥ b, which shows that the sign-changing solutions u0 and w0 are different. This completes the proof.
3. Problem (1.7) for Parameters a and b being Large
The main goal of this section is to provide a detailed multiplicity analysis of the nonsmooth elliptic problem (1.7) in dependence of the two parameters a and b. Conditions in terms of the Fučik spectrum are formulated that ensure the existence of sign-changing solutions. As for the precise formulation of this result we recall the Fučik spectrum, see, for example, [13].
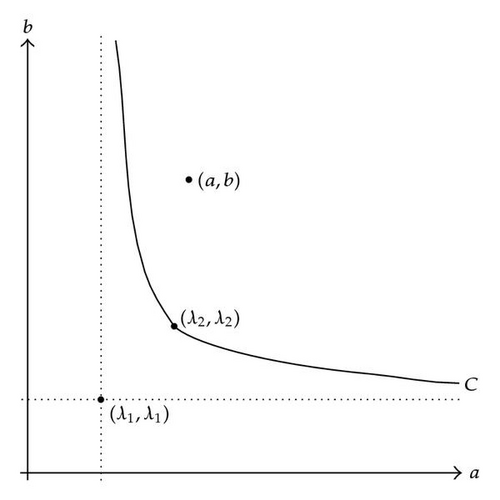
3.1. Hypotheses, Definitions, and Preliminaries
-
(g1) (x, s) ↦ g(x, s) is measurable in each variable separately.
-
(g2) There exists c > 0, and q ∈ [p, p*) such that
(3.3)for a.a. x ∈ Ω and for all s ∈ ℝ, where p* denotes the critical Sobolev exponent which is p* = Np/(N − p) if p < N, and p* = +∞ if p ≥ N. -
(g3) One has
(3.4) -
(g4) One has
(3.5)
Lemma 3.1. Suppose un → u in V0, wn⇀w in Lq′(Ω), and wn ∈ ∂𝒢(un) for all n ∈ ℕ. Then w ∈ ∂𝒢(u).
Definition 3.2. A function u ∈ V0 is called a solution of (1.7) if there is an η ∈ Lq′(Ω) such that
Remark 3.3. Due to assumption (g3) we have g1(x, 0) ≤ 0 ≤ g2(x, 0) for almost all x ∈ Ω. Hence, in view of (3.8), problem (1.7) always possesses the trivial solution.
Definition 3.4. A function is called a subsolution of (1.7) if , and if there is an such that
Similarly, we define a supersolution as follows.
Definition 3.5. A function is called a supersolution of (1.7) if , and if there is an such that
Lemma 3.6. Let e be the uniquely defined solution of (2.6). If a > λ1, then there exists a constant αa > 0 such that for any b ∈ ℝ the function αae is a positive supersolution of problem (1.7).
Proof. Let a > λ1. By (g4) there is sa > 0 such that
In a similar way the following lemma on the existence of a negative subsolution can be proved.
Lemma 3.7. Let e be the uniquely defined solution of (2.6). If b > λ1, then there exists a constant βb > 0 such that for any a ∈ ℝ the function −βbe is a negative subsolution of problem (1.7).
In the next lemma we demonstrate that small constant multiples of φ1 may be sub- and supersolutions of (1.7). More precisely we have the following result.
Lemma 3.8. Let φ1 be the normalized positive eigenfunction corresponding to the first eigenvalue λ1 of (−Δp, V0). If a > λ1, then for ε > 0 sufficiently small and any b ∈ ℝ the function εφ1 is a positive subsolution of problem (1.7). If b > λ1, then for ε > 0 sufficiently small and any a ∈ ℝ the function −εφ1 is a negative supersolution of problem (1.7).
Proof. By (g3) there is a constant δa > 0 such that
Applying a recently obtained comparison result that holds for even more general elliptic inclusions (see [38, Theorem 4.1, Corollary 4.1] we immediately obtain the following theorem.
3.2. Extremal Constant-Sign Solutions and Their Variational Characterization
Combining the results of Lemmas 3.6, 3.7, and 3.8 and Theorem 3.9 we immediately deduce the existence of nontrivial positive solutions of problem (1.7) provided the parameter a satisfies a > λ1 that and the existence of negative solutions of problem (1.7) provided that the parameter b satisfies b > λ1. Our main goal of this section is to show that problem (1.7) has a smallest positive solution and a greatest negative solution . More precisely the following result will be shown.
Theorem 3.10. Let hypotheses (g1)–(g4) be fulfilled. For every a > λ1 and b ∈ ℝ there exists a smallest positive solution of (1.7) within the order interval [0, αae] with the constant αa > 0 as in Lemma 3.6. For every b > λ1 and a ∈ ℝ there exists a greatest negative solution of (1.7) within the order interval [−βb e, 0] with the constant βb > 0 as in Lemma 3.7.
Proof. Let a > λ1. Lemmas 3.6 and 3.8 ensure that is a supersolution of problem (1.7) and is a subsolution of problem (1.7) provided that ε > 0 is sufficiently small. We may choose ε > 0 such that, in addition, εφ1 ≤ αae. Thus by Theorem 3.9 there exists a smallest and a greatest solution of (1.7) within the ordered interval [εφ1, αae]. Let us denote the smallest solution by uε. Moreover, the nonlinear regularity theory for the p-Laplacian (cf., e.g., [27, Theorem 1.5.6]) and Vázquez′s strong maximum principle [28] ensure that . Thus for every positive integer n sufficiently large there is a smallest solution of problem (1.7) within [(1/n)φ1, αae]. In this way we inductively construct a sequence (un) of smallest solutions which is monotone decreasing; that is, we have
Claim 1. u+ is a solution of problem (1.7).
As u+ belongs, in particular, to L∞(Ω), Claim 1 and Assumption (g2) implies Δpu+ ∈ L∞(Ω). The nonlinear regularity theory (cf., e.g., Theorem 1.5.6 in [27]) ensures that for some γ ∈ (0,1), so . In view of (g2) (g3) a constant can be found such that
Claim 2. .
Claim 3. is the smallest positive solution of (1.7) in [0, αae].
The proof of the existence of the greatest negative solution of (1.7) within the ordered interval [−βbe, 0] can be done in a similar way. This completes the proof of the theorem.
Lemma 3.11. Let u+ and u− be the extremal constant-sign solutions of (1.7). Then the following holds.
Proof. To prove (i) let v be a critical point of E+, that is, 0 ∈ ∂E+(v), which results in
The following lemma provides a variational characterization of the extremal constant-sign solutions u+ and u−.
Lemma 3.12. Let a > λ1 and b > λ1. Then the extremal positive solution u+ of (1.7) is the unique global minimizer of the functional E+, and the extremal negative solution u− of (1.7) is the unique global minimizer of the functional E−. Both u+ and u− are local minimizers of E0.
Proof. The functional E+ : V0 → ℝ is bounded below, coercive, and weakly lower semicontinuous. Thus there exists a global minimizer v+ ∈ V0 of E+, that is,
Lemma 3.13. The functional E0 : V0 → ℝ has a global minimizer v0 which is a nontrivial solution of (1.7) satisfying u− ≤ v0 ≤ u+.
Proof. One easily verifies that E0 : V0 → ℝ is coercive and weakly lower semicontinuous, and thus a global minimizer v0 exists which is a critical point of E0. Apply Lemma 3.11(iii) and note that, for example, E0(u+) = E+(u+) < 0, which shows that v0 ≠ 0.
3.3. Sign-Changing Solutions
Theorem 3.10 ensures the existence of a smallest positive solution in [0, αa e] and a greatest negative solution of (1.7) in [−βbe, 0]. The idea to show the existence of sign-changing solutions is to prove the existence of nontrivial solutions u0 of (1.7) satisfying u− ≤ u0 ≤ u+ with u0 ≠ u− and u0 ≠ u+, which then must be sign-changing, because u+ and u− are the extremal constant-sign solutions.
Theorem 3.14. Let hypotheses (g1)–(g4) and (H) be satisfied. Then problem (1.7) has a smallest positive solution in [0, αa e], a greatest negative solution in [−βbe, 0], and a nontrivial sign-changing solution with u− ≤ u0 ≤ u+.
Proof. Clearly the existence of the extremal positive and negative solution u+ and u− follows from Theorem 3.10, because (H), in particular, implies that a > λ1 and b > λ1. As for the existence of a sign-changing solution we first note that by Lemma 3.13 it follows that the global minimizer v0 of E0 is a nontrivial solution of (1.7) satisfying u− ≤ v0 ≤ u+. Therefore, if v0 ≠ u+ and v0 ≠ u−, then v0 = u0 must be a sign-changing solution as asserted, because u− is the greatest negative and u+ is the smallest positive solution of (1.7). Thus, we still need to prove the existence of sign-changing solutions in case that either v0 = u− or v0 = u+.
Let us consider the case v0 = u+ only, since the case v0 = u− can be treated quite similarly. By Lemma 3.12, u− is a local minimizer of E0. Without loss of generality we may even assume that u− is a strict local minimizer of E0, because on the contrary we would find (infinitely many) critical points z of E0 that are sign-changing solutions thanks to u− ≤ z ≤ u+ and the extremality of the solutions u−, u+ obtained in Theorem 3.10 which proves the assertion.
Therefore, it remains to prove the existence of sign-changing solutions under the assumptions that the global minimizer v0 of E0 is equal to u+, and u− is a strict local minimizer of E0. This implies the existence of ρ ∈ (0, ∥u− − u+∥) such that
Remark 3.15. The multiplicity results and the existence of sign-changing solutions obtained in this section generalize very recent results due to the authors obtained in [3, 4, 7]. Moreover, if the function t ↦ g(x, t) is continuous on ℝ and a = b = λ, then ∂G(x, ξ) = {g(x, ξ)}, and problem (1.7) reduces to
Remark 3.16. Theorem 3.14 improves also Corollary 3.2 of [8]. In fact, let p = 2, let u ∈ V0 be a solution of (1.7) in case a = b = λ and g(x, t) ≡ g(t), (x, t) ∈ Ω × ℝ with η ∈ Lq′(Ω) satisfying η(x) ∈ ∂G(u(x)). By definition of Clarke′s gradient we have, for any φ ∈ V0,
Remark 3.17. Multiplicity results for a nonsmooth version of problem (1.4) in form of (1.2) can be established under structure conditions for Clarke′s gradient ∂j similar to H(f).
Multiplicity and sign-changing solutions results have been obtained recently in [43] for the following nonlinear Neumann-type boundary value problem: find u ∈ V∖{0} and parameters a, b ∈ ℝ such that




