We demonstrate how to fast construct quantum error-correction codes based on quadratic residues Pauli block transforms. The present quantum codes have an advantage of being fast designed from Abelian groups on the basis of Pauli block matrices that can be yielded from quadratic residues with much efficiency.

1. Introduction

The applications of the Legendre symbol have been already suggested in signal processing, communication, image compression, cryptography, and so forth [1, 2].

Provided a finite field GF(q), Euler’s criterion ℒ_q(x) for the Legendre symbol is defined by

(1.1)

where q is a power of an odd prime number. Namely, ℒ_q(0) = 0, ℒ_q(x) = 1 if x = y² for some element y ∈ GF(q), and ℒ_q(x) = −1 if x ≠ y² for any element in GF(q). Based on quadratic residues in GF(q), one defines a matrix

(1.2)

with the elements a_ij = ℒ_q(i − j).

Lemma 1.1. Taking any two rows of Q_q, that is, for s ≠ 0, it follows

(1.3)

Currently, the striking development in quantum error-correction codes (QECCs) is the employment of the stabilizer formalism, whereby code words are subspaces in Hilbert space specified by Abelian groups. The problem of constructing QECCs was reduced to that of searching for the classical dual-containing (or self-orthogonal) codes [3–8]. The virtue of this approach is that QECCs can be directly constructed from classical codes with a certain property, rather than developing a completely new coding theory of QECCs from scratch. Unfortunately, the need for dual-containing codes presents a substantial obstacle to the quantum coding theory in its entirety, especially in the context of modern codes, such as low-density parity-check quantum codes [7]. To resolve this problem, we consider the construction of QECCs over the finite field GF(q) by employing the matrix Q_n in (1.2). Namely, we first replace all entries of Q_n with Pauli matrices and obtain the Pauli block matrix 𝒬_n. After that, we extend this kind of block matrices for the large-size Pauli block matrices by using the recursive techniques with the fast matrix block transforms [9–12]. Since all row operations that are obtained from rows of 𝒬_n are independent and commutative, an Abelian group can be generated elegantly. Therefore, a type of quantum code is generated structurally via the stabilizer formalism. This approach provides the great flexibility in designing quantum codes with large code length and hence allows for an advantage of being simply constructed with the low complexity.

This paper is organized as follows. In Section 2, three kinds of Pauli block matrices are constructed. In Section 3, according to the properties of Pauli block matrices, Abelian groups can be generated with efficiency. In Section 4, we investigate constructions of quantum codes based on the stabilizer formalism. Finally, conclusions are drawn in Section 5.

2. Pauli Block Matrices

Pauli matrices have been widely applied in signal processing [11], quantum information and quantum computing [3, 13], and so forth. In this section, we investigate constructions of several types of Pauli block matrices according to the structure of Hadamard transforms based on these Pauli matrices.

2.1. Pauli Matrices

Pauli matrices are defined by 𝒫 = {σ_j : 0 ≤ j ≤ 3}, where

(2.1)

where

. For simplicity, we denote the 2 × 2 identity matrix σ₀ by a block matrix ℐ throughout this paper.

Pauli matrices in 𝒫 have the following basic properties:

(2.2)

2.2. Pauli Block Matrice

Definition 2.1. Denote , then 𝒬 is a Pauli block matrix if and only if all entries [a]_ij belong to 𝒫, that is, [a]_ij ∈ 𝒫.

Based on the matrix Q_q in (1.2), we propose several approaches for constructions of Pauli block matrices for any two entries σ_i, σ_j ∈ 𝒫∖{σ₀}.

Construction. Taking a matrix Q_q in (1.2), it follows two kinds of Pauli block matrices:

(1)
, which is constructed by replacing “0,1” in Q_q with σ_i and “−1” with σ_j,
(2)
, which is constructed by replacing “1” in Q_q with σ_i and “−1,0” with σ_j.

Specially, one achieves two types of Pauli block matrices.

Construction. If q = 4m + 3 for any positive integer m, then the (q + 1)×(q + 1) matrix can be constructed as

(2.3)

where t denotes the all-1 column vector of the length q and I is the (q + 1)×(q + 1) identity matrix. As a result, there are two types of Pauli block matrices:

(1)
, which is constructed by replacing “0,1” in Q_q+1 with σ_i and “−1” with σ_j,
(2)
, which is constructed by replacing “1” in Q_q+1 with σ_i and “−1,0” with σ_j.

Construction. If q = 4m + 1 for any positive integer m, then one constructs the 2(q + 1) × 2(q + 1) matrix Q_2(q+1) by replacing “0” in the matrix

(2.4)

with the block matrix [R₀] and “±1” with the matrix [R_±1], where

(2.5)

Then, there are two Pauli block matrices:

(1)
, which is constructed by replacing “0,1” in Q_2(q+1) with σ_i and “−1” with σ_j,
(2)
, which is constructed by replacing “1” in Q_2(q+1) with σ_i and “−1,0” with σ_j.

2.3. Fast Constructions of Pauli Block Matrices

To construct the large-order Pauli block matrices, we first introduce the Kronecker product of two matrices and B = (b_ij) _s×t, that is,

(2.6)

With a little abuse, we denote the Kronecker product by using the notation “⊗” throughout this paper.

Making use of the Kronecker product of Pauli block matrices [9–12], a family of Pauli block matrices may be extended.

Theorem 2.2. Suppose that 𝒬_q and 𝒬_p are two Pauli block matrices. For any nonnegative integer numbers s and m, a large-order block Jacket matrix may be constructed (or decomposed) in the following way:

(2.7)

Proof. Based on an arbitrary Pauli block matrix 𝒬_r, the large-order Pauli block matrices for l ≥ 2 can be obtained by using the recursive relations:

(2.8)

where r ∈ {p, q} and l ∈ {s, m}. According to the properties of the Kronecker product, it is easy to calculate

(2.9)

and then this completes the proof of the theorem.

Employing Pauli Block matrices 𝒬_n in Constructions 1, 2, and 3 with respect to the Kronecker product in (2.7), any large-order Pauli block matrices can be constructed with the fast algorithm. The computational complexity of the proposed algorithm is shown in Table 1.

Table 1. Computation complexity of the fast algorithm based on Pauli block matrices. For simplicity, Add and Mul denote the number of additions and multiplications. The notations

and

express the number of nonidentity matrices σ₀ in Pauli block matrices Q_p and Q_q.

	Direct approach	Proposed algorithm	Proposed algorithm
Add	(n − 1)n	(p − 1)nm	pn + qn − 2n
Mul	n²

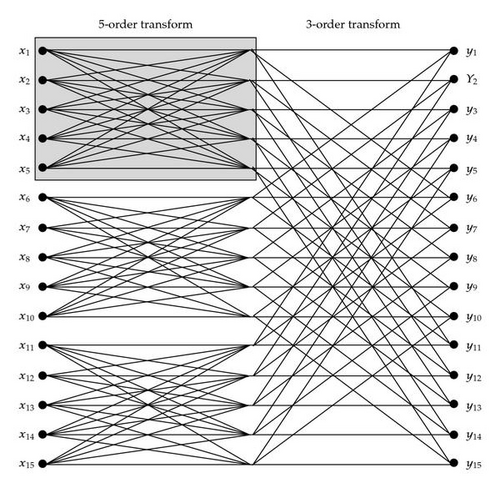
As an example, the construction of 𝒬₁₅ = 𝒬₃ ⊗ 𝒬₅ is depicted in Figure 1. According to Table 1, the computation of the Pauli block matrix 𝒬₁₅ requires 26 additions and 34 multiplications. Compared with the directed computation, the proposed algorithm is obviously faster.

3. Abelian Group Based on Pauli Block Matrices

Let 𝒫^⊗n denote the set of the n-fold tensor products (the Kronecker product) of Pauli operators (matrices) in 𝒫 [13]. Then 𝒫^⊗n, together with possible multiplicative factors in {±i, ±1}, form a group of n-qubit operations, denoted by 𝒢_n. An arbitrary operation α_u ∈ 𝒢_n can be uniquely expressed by

(3.1)

where x_ut, z_ut ∈ {0,1} for 1 ≤ t ≤ n. Omitting factor i^λ, we denote α_u by a concatenated 2n-dimensional vector

[6]:

(3.2)

The Hamming weight of is the number of (x_uh∣z_uh) (1 ≤ h ≤ n) such that (x_uh∣z_uh)≠(0∣0). The symplectic inner product of any two vectors and is defined by

(3.3)

where

and

. According to [6], two operations α_u and α_v commute if and only if

(3.4)

The symplectic inner product of two vectors is important since it can be used conveniently to search for generators of an Abelian subgroup 𝒮⊆𝒢_n.

Assume that each row of a Pauli block matrix 𝒬_n is denoted by for 1 ≤ i ≤ n, from which an n-qubit operation, called as the row operator, can be obtained as

(3.5)

Based on properties of the Kronecker product [11, 14, 15], we achieve the commutativity of row operators for Pauli block matrices 𝒬_n.

Theorem 3.1. For Pauli block matrices 𝒬_n proposed in Construction 1 (also for Constructions 2 and 3), all independent row operators of 𝒬_n are commuting and hence generate an Abelian group.

Proof. Employing Pauli block matrices 𝒬_n that are constructed via substituting Pauli matrices for the entries of the Hadamard matrices, all row operators of 𝒬_n can be expressed by the concatenated vectors in (3.2), from which the n × 2n matrices (H_x∣H_z) can hence be constructed. According to the properties of the Hadamard matrices, it is easy to calculate

(3.6)

which implies that all independent n-qubit row operators of 𝒬_n are commuting [5].

Corollary 3.2. Considering any two given Pauli block matrices 𝒬_p and 𝒬_q, all independent pq-qubit row operators of the Kronecker product 𝒬_pq = 𝒬_p ⊗ 𝒬_q are commuting.

Example 3.3. We consider GF(3) = {0,1, 2} with the nonzero squares 1² = 1mod 3 and 2² = 1 mod 3, and hence ℒ₃(0) = 0, ℒ₃(1) = 1, and ℒ₃(2) = −1. With the rows and columns of a matrix Q₃ being indexed by {0,1, 2}, one obtains

(3.7)

According to Construction 1, one gains the Pauli block matrix:

(3.8)

Taking i = 1 and j = 3, one has the concatenated matrix:

(3.9)

It is easy to check that

, which means that three row operators of

(3.10)

are commuting.

For another, based on Construction 2, one obtains

(3.11)

from which the Pauli block matrix

can be achieved:

(3.12)

Taking i = 1 and j = 3, one has the concatenated matrix:

(3.13)

from which it is easy to check that all row operators of

are commuting.

Example 3.4. According to GF(5) with ℒ₅(1) = ℒ₅(4) = 1 mod 5 and ℒ₅(2) = ℒ₅(3) = −1 mod 5, if the rows and columns of Q₅ are indexed by GF(5), one gets

(3.14)

Employing Construction 1, we get the Pauli block matrix:

(3.15)

Taking i = 1 and j = 3, one has

(3.16)

which means that five row operators of

for i = 1 and j = 3 are commuting.

Furthermore, according to Construction 3 with respective Q₅ in (3.14), one obtains a Pauli block matrix for i = 1 and j = 3 with the concatenated matrix H₁₀ expressed as

(3.17)

It is obvious that all row operators of

are commuting.

4. The Stabilizer Quantum Codes

In this section, we construct quantum codes C(𝒮) by using Pauli block matrices 𝒬_n with commutative row operators, from which n − k independent row operators can be selected as generators of an Abelian group 𝒮.

Given an Abelian subgroup 𝒮 of 𝒢_n, the stabilizer quantum code C(𝒮) is a set of n-qubit quantum states {|ψ〉} associated with 𝒮, that is,

(4.1)

which is the subspace fixed by 𝒮 (called as the stabilizer). For an [[n, k, d]] stabilizer quantum code, which encodes k logical qubits into n physics qubits, C(𝒮) has dimension 2^k and 𝒮 has 2^n−k independent operators.

To construct such a quantum code, the sticking point is to search for an Abelian group, the stabilizer 𝒮, from which the code C(𝒮) can be structurally generated through (4.1).

Theorem 4.1. Given a Pauli block matrix 𝒬_n with commutative row operators, the stabilizer quantum code C(𝒮) can be constructed with parameters [[n, k, d]] where the stabilizer 𝒮 is a set of n-qubit operators generated from n − k independent row operators of Pauli block matrix 𝒬_n.

Proof. Suppose that there are r (r ≥ n − k) independent rows of 𝒬_n. Then n − k generators of the stabilizer 𝒮 can be generated by selecting n − k rows from these r independent rows of 𝒬_n provided n − k ≤ r. Namely, any n − k operators can be selected to generate an Abelian group:

(4.2)

which is a stabilizer in essence. By making use of (4.1), a stabilizer quantum code [[n, k, d]] can be generated from 𝒮. According to the quantum Singleton bound proposed in [6], it follows that k ≤ n − 2d + 2. This completes the proof of the theorem.

Example 4.2. We consider the Pauli block matrix 𝒬₅ in (3.15) with the concatenated matrix in (3.16). It is known that all rows of H₅ are independent. Thus, any 5 − k rows of H₅, denoted by , can be selected to generate the stabilizer 𝒮 with 5 − k generators. According to the construction conditions of quantum codes in [5], we get the generator matrix of quantum codes satisfying

(4.3)

which can be rewritten as

(4.4)

where

. To construct such a quantum code, we assume that there exists one unitary matrix U such that

(4.5)

According to (4.4), the generator matrix g is calculated:

(4.6)

from which quantum codes can be constructed with the parameters [[5,0, 4]], [[5,1, 2]], [[5,2, 1]], [[5,3, 1]], and [[5,4, 1]].

Taking the quantum code [[5,1, 2]] as an example, we select 4 rows to generate the matrix:

(4.7)

From (4.4), we get

(4.8)

Therefore, a quantum code [[5,1, 2]] can be constructed from (4.8), where d = 2, the Hamming weight of 𝒢₅, can be calculated from the Hamming weight of the bitwise or of

with

Example 4.3. Suppose n = 10, and then we consider Pauli block matrix for i = 1 and j = 3 with the concatenated matrix in (3.17). It is obvious that all rows of H₁₀ are independent and commutative. Selecting any 10 − k (0 ≤ k ≤ 10) row operators from , we obtain the stabilizer , from which quantum codes can be constructed with the parameters [[10,0, 4]], [[10,1, 4]], [[10,2, 4]], [[10,3, 3]], [[10,4, 3]], [[10,5, 3]], [[10,6, 3]], [[10,7, 3]], [[10,8, 1]], and [[10,9, 1]].

5. Conclusion

A family of quantum codes is investigated with fast Pauli block transforms by using quadratic residues in the finite field GF(q). We first investigate the construction approaches based on three kinds of Pauli block matrices with commutative row operators. Then the large-order Pauli block matrices are structurally constructed via the fast Pauli block constructing transforms based on the recursive relationship of identity matrices and successively lower-order Pauli block matrices. These Pauli block matrices have such a characteristic that all row operators are independent and commutative, which can generate an Abelian operator group. Finally, an instructive approach for constructions of quantum codes is suggested via the stabilizer formalism according to the Abelian group 𝒮 yielded from Pauli block matrices. This code may provide the great flexibility in designing quantum codes with large block length through implementing the proposed fast construction algorithms.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Signal flow graph for Pauli block transform for 𝒬₁₅.

Acknowledgment

This research was supported by the WCU R-32-2008-000-20014-0 NRF, South Korea.

References

1 Gauss C. F., Disquisitiones Arithmeticae, 1986, 2nd edition, Springer, New York, NY, USA, MR837656.
10.1007/978-1-4939-7560-0
Google Scholar
2 Jacobi C. G. J., Uber die Kreisteilung und ihre Anwendung auf die Zahlentheorie, 1837, Bericht Ak. Wiss, Berlin, Germany.
Google Scholar
3 Zeng G., Li Y., Guo Y., and Lee M. H., Stabilizer quantum codes over the Clifford algebra, Journal of Physics A. (2008) 41, no. 14, 8, 145304, https://doi.org/10.1088/1751-8113/41/14/145304, MR2450394, ZBL1136.81019.
10.1088/1751-8113/41/14/145304
Google Scholar
4 Aggarwal V. and Calderbank A. R., Boolean functions, projection operators, and quantum error correcting codes, IEEE Transactions on Information Theory. (2008) 54, no. 4, 1700–1707, https://doi.org/10.1109/TIT.2008.917720, MR2450295.
10.1109/TIT.2008.917720
Web of Science® Google Scholar
5 Steane A. M., Enlargement of Calderbank-Shor-Steane quantum codes, IEEE Transactions on Information Theory. (1999) 45, no. 7, 2492–2495, https://doi.org/10.1109/18.796388, MR1725135, ZBL0960.94033.
10.1109/18.796388
Web of Science® Google Scholar
6 Calderbank A. R., Rains E. M., Shor P. W., and Sloane N. J. A., Quantum error correction via codes over GF(4), IEEE Transactions on Information Theory. (1998) 44, no. 4, 1369–1387, https://doi.org/10.1109/18.681315, MR1665774, ZBL0982.94029.
10.1109/18.681315
Web of Science® Google Scholar
7 MacKay D. J. C., Mitchison G., and McFadden P. L., Sparse-graph codes for quantum error correction, IEEE Transactions on Information Theory. (2004) 50, no. 10, 2315–2330, https://doi.org/10.1109/TIT.2004.834737, MR2097049.
10.1109/TIT.2004.834737
Web of Science® Google Scholar
8 Matsumoto R., Improvement of Ashikhmin-Litsyn-Tsfasman bound for quantum codes, IEEE Transactions on Information Theory. (2002) 48, no. 7, 2122–2124, https://doi.org/10.1109/TIT.2002.1013156, MR1930021, ZBL1061.94082.
10.1109/TIT.2002.1013156
Web of Science® Google Scholar
9 Lee M. and Zeng G., [email protected], Family of fast jacket transform algorithms, Electronics Letters. (2007) 43, no. 11, 2-s2.0-0038471654, https://doi.org/10.1049/el:20070145.
10.1049/el:20070145
Web of Science® Google Scholar
10 Lee M. H. and [email protected], Hou J., [email protected], Fast block inverse jacket transform, IEEE Signal Processing Letters. (2006) 13, no. 8, 461–464, 2-s2.0-0038471654, https://doi.org/10.1109/LSP.2006.873660.
10.1109/LSP.2006.873660
Web of Science® Google Scholar
11 Zeng G. and [email protected], Lee M. H., [email protected], A generalized reverse block jacket transform, IEEE Transactions on Circuits and Systems I. (2008) 55, no. 6, 1589–1600, 2-s2.0-0034188354, https://doi.org/10.1109/TCSI.2008.916620.
10.1109/TCSI.2008.916620
Web of Science® Google Scholar
12 Chen Z., Lee M. H., and Zeng G., Fast cocyclic jacket transform, IEEE Transactions on Signal Processing. (2008) 56, no. 5, 2143–2148, https://doi.org/10.1109/TSP.2007.912895, MR2450435.
10.1109/TSP.2007.912895
Web of Science® Google Scholar
13 Nielsen M. A. and Chuang I. L., Quantum Computation and Quantum Information, 2000, Cambridge University Press, Cambridge, UK, MR1796805.
Google Scholar
14 Lee M. H., A new reverse jacket transform and its fast algorithm, IEEE Transactions on Circuits and Systems II. (2000) 47, no. 1, 39–47, 2-s2.0-0037794853, https://doi.org/10.1109/82.818893, ZBL1064.94517.
10.1109/82.818893
Web of Science® Google Scholar
15 Lee M. H., Rajan B. S., and Park J. Y., A generalized reverse jacket transform, IEEE Transactions on Circuits and Systems II. (2001) 48, no. 7, 684–690, 2-s2.0-0038471654, https://doi.org/10.1109/82.958338, ZBL1014.65150.
10.1109/82.958338
Web of Science® Google Scholar

All articles

Fast Constructions of Quantum Codes Based on Residues Pauli Block Matrices

Abstract

1. Introduction

2. Pauli Block Matrices

2.1. Pauli Matrices

2.2. Pauli Block Matrice

2.3. Fast Constructions of Pauli Block Matrices

3. Abelian Group Based on Pauli Block Matrices

4. The Stabilizer Quantum Codes

5. Conclusion

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fast Constructions of Quantum Codes Based on Residues Pauli Block Matrices

Abstract

1. Introduction

2. Pauli Block Matrices

2.1. Pauli Matrices

2.2. Pauli Block Matrice

2.3. Fast Constructions of Pauli Block Matrices

3. Abelian Group Based on Pauli Block Matrices

4. The Stabilizer Quantum Codes

5. Conclusion

Acknowledgment

References

Figures

References

Related

Information