International Journal of Differential Equations
Volume 2010, Issue 1 461048
Research Article
Open Access

Time-Optimal Control of Systems with Fractional Dynamics

Christophe Tricaud, 

Corresponding Author

Christophe Tricaud

Center for Self-Organizing and Intelligent Systems (CSOIS), Department of Electrical and Computer Engineering, Utah State University, 41260 Old Main Hill, Logan, UT 84322-4160, USA usu.edu

Search for more papers by this author
YangQuan Chen, 

YangQuan Chen

Center for Self-Organizing and Intelligent Systems (CSOIS), Department of Electrical and Computer Engineering, Utah State University, 41260 Old Main Hill, Logan, UT 84322-4160, USA usu.edu

Search for more papers by this author
First published: 10 February 2010
https://doi.org/10.1155/2010/461048
Citations: 28
Academic Editor: Wen Chen

Abstract

We introduce a formulation for the time-optimal control problems of systems displaying fractional dynamics in the sense of the Riemann-Liouville fractional derivatives operator. To propose a solution to the general time-optimal problem, a rational approximation based on the Hankel data matrix of the impulse response is considered to emulate the behavior of the fractional differentiation operator. The original problem is then reformulated according to the new model which can be solved by traditional optimal control problem solvers. The time-optimal problem is extensively investigated for a double fractional integrator and its solution is obtained using either numerical optimization time-domain analysis.

1. Introduction

In the world surrounding us, the physical laws of dynamics are not always followed by all systems. When the considered systems are complex or can only be studied on a macroscopic scale, they sometimes divert from the traditional integer order dynamic laws. In some cases, their dynamics follow fractional-order laws meaning that their behavior is governed by fractional-order differential equations [1]. As an illustration, it can be found in the literature [2] that materials with memory and hereditary effects, and dynamical processes, such as gas diffusion and heat conduction, in fractal porous media can be more precisely modeled using fractional-order models than using integer-order models. Another vein of research has identified the dynamics of a frog′s muscle to display fractional-order behavior [3].

Optimal Control Problems (OCPs) or Integer-Order Optimal Controls (IOOCs) can be found in a wide variety of research topics such as engineering and science of course, but economics as well. The field of IOOCs has been investigated for a long time and a large collection of numerical techniques has been developed to solve this category of problems [4].

The main objective of an OCP is to obtain control input signals that will make a given system or process satisfy a given set of physical constraints (either on the system′s states or control inputs) while extremizing a performance criterion or a cost function. Fractional Optimal Control Problems (FOCPs) are OCPs in which the criterion and/or the differential equations governing the dynamics of the system display at least one fractional derivative operator. The first record of a formulation of the FOCP was given in [5]. This formulation was general but includes constraints on the system′s states or control inputs. Later, a general definition of FOCP was formulated in [6] that is similar to the general definition of OCPs. The number of publications linked to FOCPs is limited since that problem has only been recently considered.

Over the last decade, the framework of FOCPs has hatched and grown. In [5], Agrawal gives a general formulation of FOCPs in the Riemann-Liouville (RL) sense and proposes a numerical method to solve FOCPs based on variational virtual work coupled with the Lagrange multiplier technique. In [7], the fractional derivatives (FDs) of the system are approximated using the Grünwald-Letnikov definition, providing a set of algebraic equations that can be solved using numerical techniques. The problem is defined in terms of the Caputo fractional derivatives in [8] and an iterative numerical scheme is introduced to solve the problem numerically. Distributed systems are considered in [9] and an eigenfunction decomposition is used to solve the problem. Özdemir et al. [10] also use eigenfunction expansion approach to formulate an FOCP of a 2-dimensional distributed system. Cylindrical coordinates for the distributed system are considered in [11]. A modified Grünwald-Letnikov approach is introduced in [12] which leads to a central difference scheme. Frederico and Torres [13–15], using similar definitions of the FOCPs, formulated a Noether-type theorem in the general context of the fractional optimal control in the sense of Caputo and studied fractional conservation laws in FOCPs. In [6], a rational approximation of the fractional derivatives operator is used to link FOCPs and the traditional IOOCs. A new solution scheme is proposed in [16], based on a different expansion formula for fractional derivatives.

In this article, we introduce a formulation to a special class of FOCP: the Fractional Time-Optimal Control Problem (FTOCP). Time-optimal control problems are also referred to in the literature as minimum-time control problems, free final time-optimal control, or bang-bang control problems. These different denominations define the same kind of optimal control problem in which the purpose is to transfer a system from a given initial state to a specified final state in minimum time. So far, this special class of FOCPs has been disregarded in the literature. In [6], such a problem was solved as an example to demonstrate the capability and generality of the proposed method but no thorough studies were done.

The article is organized as follows. In Section 2, we give the definitions of fractional derivatives in the RL sense and FOCP and introduce the formulation of FTOCP. In Section 3, we consider the problem of the time-optimal control of a fractional double integrator and propose different schemes to solve the problem. In Section 4, the solution to the problem is obtained for each approach for a given system. Finally, we give our conclusions in Section 5.

2. Formulation of the Fractional Time-Optimal Control Problem

2.1. The Fractional Derivative Operator

There exist several definitions of the fractional derivative operator: Riemann-Liouville, Caputo, Grünwald-Letnikov, Weyl, as well as Marchaud and Riesz [17–20]. Here, we are interested in the Riemann-Liouville definition of the fractional derivatives for the formulation of the FOCP.

The Left Riemann-Liouville Fractional Derivative (LRLFD) of a function f(t) is defined as
(2.1)
where Γ(·) is the Gamma function defined for any complex number z as
(2.2)
and where the order of the derivative α satisfies n − 1 ≤ α < n. The Right Riemann-Liouville Fractional Derivative (RRLFD) is defined as
(2.3)

2.2. Fractional Optimal Control Problem Formulation

With the RL definition of the fractional derivatives operator given in (2.1) and (2.3), we can specify a general FOCP: find the optimal control u(t) for a fractional dynamical system that minimizes the following performance criterion:
(2.4)
subject to the following system dynamics:
(2.5)
with initial condition
(2.6)
and with the following constraints:
(2.7)
where x is the state variable, t ∈ [a, b] stands for the time, and L, G, and H are arbitrary given nonlinear functions. The subscripts o, ti, ei, and ee on the functions G(·, ·) and L(·, ·, ·) stand for, respectively, objective function, trajectory constraint, endpoint inequality constraint and endpoint equality constraint.

2.3. Fractional Time-Optimal Control Problem Formulation

A FTOCP is defined by a performance index of the form
(2.8)
which appears when we desire to minimize the time required to reach a given target xb given some initial conditions xa.
Under such conditions, the problem is to transfer the system whose dynamics are given by
(2.9)
from a given initial state x(a) = xa to the desired state x(b) = xb. The minimum time required to reach the target is defined as t*.
To ensure that the problem has a solution, the control variables are required to be constrained in the following way:
(2.10)
In the following, we will make use of the minimum principle to determine the optimal control law u*(t) for the previously defined problem. We define the state associated with the optimal control law as x*(t).
We define the Hamiltonian ℋ for the problem described by the dynamic system (2.9) and the criterion (2.8) as
(2.11)
where λ(t) stands for the costate variable. The optimal costate variable is defined as λ*(t).
In the case of constrained systems, the results given in [5] do not apply as the control function u(t) is constrained and does not have arbitrary variations. Indeed, if the control u(t) lies on the boundary in (2.10), then the variations are not arbitrary. Instead, we need to use Pontryagin′s minimum principle [4]. According to the proof of the theorem in [21], we use for demonstration arbitrary variations in the control signal u(t) = u*(t) + δu(t). We define both the increment ΔJ and the (first) variation δJ of the performance index J as
(2.12)
where the first variation is defined as
(2.13)
With the constraints (2.10) and making the assumption that all the admissible variations on the control ∥δu(t)∥ are small enough to ensure that the sign of the increment ΔJ can be determined by the sign of the variation δJ, the necessary condition on u* to minimize J becomes
(2.14)
According to [21, Chapter 2], the first variation can be defined as
(2.15)
In the previous equation,
  • (1)

    if the optimal state x* equations are satisfied, then we obtain the state relation,

  • (2)

    if the costate λ* is chosen so that the coefficient of the dependent variation δx in the integrand is identically zero, then we obtain the costate equation,

  • (3)

    the boundary condition is chosen so that it results in the auxiliary boundary condition.

When all of the previous enumerated items are satisfied, the first variation can be reformulated as
(2.16)
The integrand in the previous relation is the first-order approximation to change in the Hamiltonian ℋ due to a change in u alone. This means that by definition
(2.17)
combining the previous two equations leads us to
(2.18)
Now, using the above, the necessary condition becomes
(2.19)
for all admissible δu less than a small value. The relation becomes
(2.20)
Replacing u* + δu by u, the necessary condition becomes
(2.21)
When applied to our problem, we obtain
(2.22)
which can be simplified to
(2.23)
The state and costate equations can be retrieved from [5] and give
(2.24)
with
(2.25)
where we again note that b is free. We can notice that u* is the control signal that causes G(x*, u, t) to take its minimum value.
Let us consider the simple case of a fractional system with the following: dynamics
(2.26)
The state and costate equations become
(2.27)
with
(2.28)
Using Pontryagin′s minimum principle, we have
(2.29)
Defining q* = bλ* gives us
(2.30)
(2.31)
We can now derive the optimal control sequence u*(t). Given (2.31),
  • (1)

    if q*(t) is positive, then the optimal control u*(t) must be the smallest admissible control umin  value so that

    (2.32)

  • (2)

    and if q*(t) is negative, then the optimal control u*(t) must be the largest admissible control umax  value so that

    (2.33)

Combining (2.32) and (2.33) gives us the following control law:
(2.34)
In Section 3, we provide several numerical methods to obtain the control u, state x, and costate λ for a specific problem from the literature.

3. Solution of the Time-Optimal Control of a Fractional Double Integrator

In this section, we consider the following FTOCP:
(3.1)
subject to
(3.2)

3.1. Solution Using Rational Approximation of the Fractional Operator

It is possible for time-optimal control problems to be reformulated into traditional optimal control problems by augmenting the system dynamics with additional states (one additional state for autonomous problems). For that purpose, the first step is to specify a nominal time interval, [a  b], for the problem and to define a scaling factor, adjustable by the optimization procedure, to scale the system dynamics, and hence, in effect, scale the duration of the time interval accordingly. This scale factor and the scaled time are represented by the extra states.

The problem defined by (3.1)-(3.2) can accordingly be reformulated as follows: find the control u(t) (satisfying umin  ≤ u(t) ≤ umax ) over the time interval [01], which minimizes the quadratic performance index
(3.3)
subject to the following dynamics:
(3.4)
where the initial conditions are
(3.5)
where T(0) is the initial value chosen by the user. Final state constraints are
(3.6)
According to [22], we can approximate the operator using a state space definition
(3.7)
Such approximation is called rational approximation of the fractional operator. To ensure the applicability of our method, we need to define a new state vector y(t) such that
(3.8)
where z(t) is the state vector of the rational approximation for the fractional-order system described by .
Using the methodology proposed in [6], we reformulate the problem defined by (3.1)-(3.2). Find the control u(t) (satisfying umin  ≤ u(t) ≤ umax ), which minimizes the quadratic performance index
(3.9)
subjected to the following dynamics:
(3.10)
the initial condition
(3.11)
and the final state constraints given by
(3.12)

Such a definition allows the problem to be solved by any traditional optimal control problem solver.

3.2. Solution Using Bang-Bang Control Theory

The solution to the problem defined by (3.1)–(3.2) can also be solved using bang-bang control theory. In the integer case (α = 1), the solution in the time domain is well documented and is given by
(3.13)
where T1 is the switching time.
Such a solution is obtained by deriving the system′s dynamic equations in the time domain: for t ∈ [0, T1] (acceleration)
(3.14)
and for t ∈ [T1, T] (deceleration)
(3.15)
Finding the switching time T1 and the final time T can be done by solving the system of final time conditions:
(3.16)
We can apply a similar technique to solve the fractional problem. For t ∈ [0, T1] (acceleration)
(3.17)
and for t ∈ [T1, T2] (deceleration)
(3.18)
Finding the switching time T1 and the final time T can be achieved by solving the system of final time conditions:
(3.19)
When expanded, it becomes
(3.20)
Renaming T21 = T − T1, we get
(3.21)
The solution to the system of equations is as follows: solve for T21
(3.22)

4. Results

In this section, we find the solution to the problem defined in Section 3 for the following parameter values:

  • (i)

    umin  = −2,

  • (ii)

    umax  = 1,

  • (iii)

    A = 300.

The analytical solution for this system for α = 1 (the traditional double integrator) is given in [23] by T* = 30 as
(4.1)
To solve the problem, we use the RIOTS_95 Matlab Toolbox [24]. The acronym RIOTS means “recursive integration optimal trajectory solver.” It is a Matlab toolbox developed to solve a wide variety of optimal control problems. For more information about the toolbox, please refer to [25].

Figure 1 shows the states x(t) as functions of t for α = 1. Figures 2, 3, 4, 5, and 6 show the state x(t) as functions of t for different values of α (0.9, 0.8, 0.7, 0.6, and 0.5, respectively). We can observe that when the order α approaches 1, the optimal duration nears its value for the double integrator case.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 0.9.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 0.8.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 0.7.
Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 0.6.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
States x(t) as functions of time t for the Bang-Bang control problem for α = 0.5.

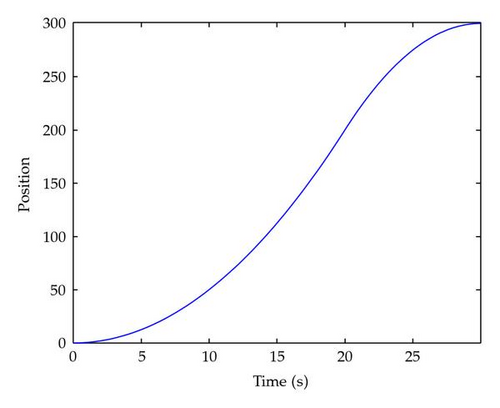
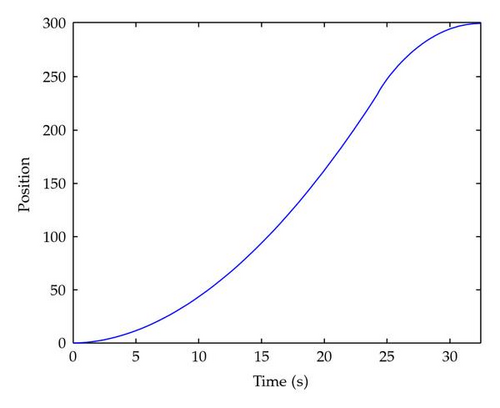
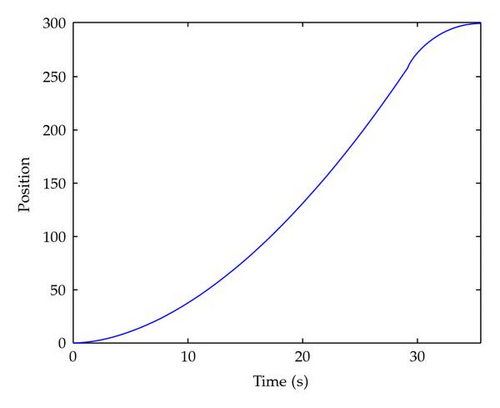
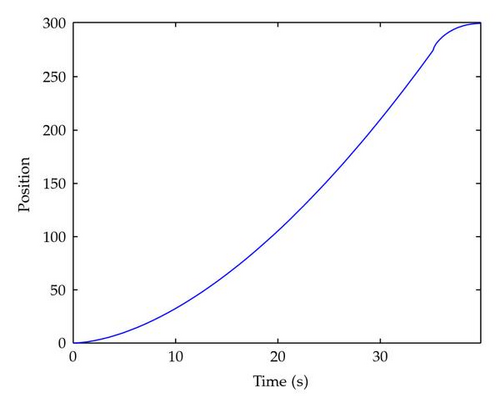
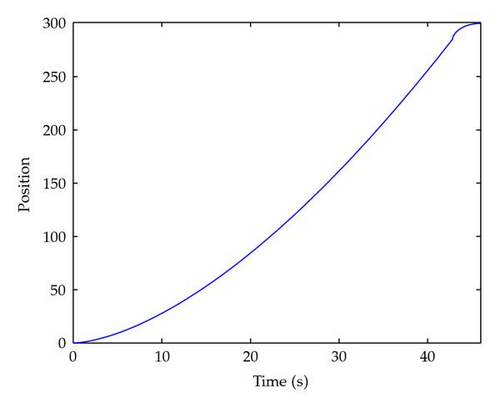
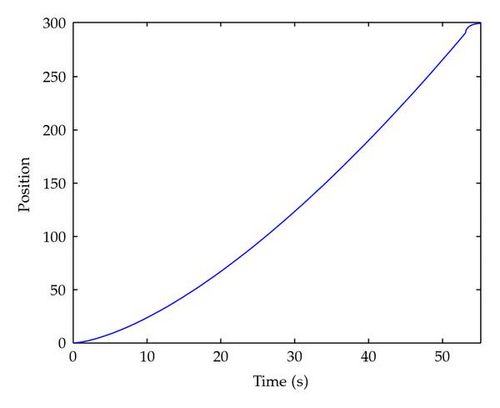
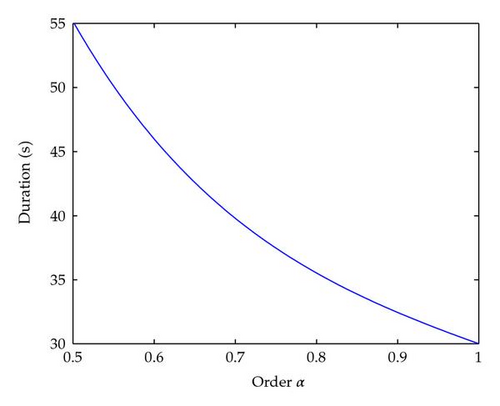
Since it is possible to obtain the analytical solution of the problem from (3.22), we give in Figure 7 the plot of the duration of the control T versus the order of the fractional derivative. As we can see, for α = 1, the solution matches the results obtained for a double integrator.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Duration of the control T as a function of the order α.

5. Conclusions

We developed a formulation for fractional time-optimal control problems. Such problems occur when the dynamics of the system can be modeled using the fractional derivatives operator. The formulation made use of the the Lagrange multiplier technique, Pontryagin′s minimum principle, and the state and costate equations. Considering a specific set of dynamical equations, we were able to demonstrate the bang-bang nature of the solution of fractional time-optimal control problems, just like in the integer-order case. We were able to solve a special case using both optimal control theory and bang-bang control theory. The optimal control solution can be obtained using a rational approximation of the fractional derivative operator whereas the bang-bang control solution is derived from the time-domain solution for the final time constraints. Both methods showed similar results, and in both cases as the order α approaches the integer value 1, the numerical solutions for both the state and the control variables approach the analytical solutions for α = 1.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.