Riesz potentials (also called Riesz fractional derivatives) and their Hilbert transforms are computed for the Korteweg-de Vries soliton. They are expressed in terms of the full-range Hurwitz Zeta functions ζ₊(s, a) and ζ₋(s, a). It is proved that these Riesz potentials and their Hilbert transforms are linearly independent solutions of a Sturm-Liouville problem. Various new properties are established for this family of functions. The fact that the Wronskian of the system is positive leads to a new inequality for the Hurwitz Zeta functions.

1. Introduction

In recent years the theory of fractional derivatives and integrals called Fractional Calculus has been steadily gaining importance for applications. Ordinary and partial differential equations of fractional order have been widely used for modeling various processes in physics, chemistry, and engineering (see, e.g., [1–3] and the references therein). Recent theoretical developments shed new light on the interpretation and properties of fractional derivatives. Having written the latter in the form of Stieltjes integrals, Podlubny [4] found new physical and geometric interpretation of these structures relating them to inhomogeneity of time. Extension of the classical maximum principle to the case of a time-fractional diffusion equation appeared in the recent work of Luchko [5]. In the present paper we are concerned with Riesz fractional derivatives (also called Riesz potentials; see [6, page 88], and [7, page 117]) that are defined as fractional powers of the Laplacian D^α = (−Δ) ^α/2 with α ∈ ℝ. They are well known for their role in investigating the solvability of nonlinear partial differential equations, and the Korteweg-de Vries equation (KdV henceforth) in particular (see, e.g., [7–11] and the references therein). In the current work, Riesz potentials of KdV solitons are computed and their relation to ordinary differential equations is established.

We continue the study of Riesz fractional derivatives of solutions to Korteweg-de-Vries-type equations started in [12]. After appropriate rescaling, KdV can be written in the form

()

It is well known that the fundamental solution of the Cauchy problem for the linearized KdV is expressed in terms of the Airy function of the first kind Ai(x) and its Hilbert transform (conjugate) in terms of the Scorer function Gi(x). The papers [12–14] were devoted to the study of fractional properties of the Airy functions and their conjugates and to the establishing of related properties for KdV-type equations.

Although there exists extensive literature on solitons, as far as we know, a study of their fractional properties is still missing. A preliminary investigation of Riesz potentials for a KdV soliton was carried out in [15]. In this paper the emphasis was put on the issue of whether solitons inherit fractional properties of fundamental solutions. Riesz potentials of a soliton, u_α(X) = D^αu₀(X), where u₀(X) = 2sech² X, X = x − 4t, and , and their Hilbert transforms, v_α(X) = −Hu_α(X), were obtained in terms of the Hurwitz Zeta function of a complex argument, ζ(s, z) with s = 2 + α and z = 1/2 + iX/π. It was proved in [15] that the zero mean properties hold for both u_α(X) and v_α(X) with α > 0. This confirmed the predictions based on the properties of fundamental solutions of the linearized Cauchy problems.

The goal of the current paper is to go further and to study Riesz potentials of solitons as solutions of differential equations. We intend to show that these functions and their Hilbert transforms form linearly independent systems of solutions for a second-order ordinary differential equation in a self-adjoint form. This fact may be helpful in understanding the issue of using these structures as intrinsic mode functions in signal processing (see [16, 17] and the references therein), that is, in using Riesz potentials for expansions. In this context it is interesting to point out that the graphs of the functions u_α(X) reveal a striking similarity to those of the Airy wavelets generated by the function Ai^′(x)Ai^′(−x) (see [18, page 34], and Figure 3 below).

For the analysis to follow; we employ the full-range Hurwitz Zeta functions: ζ₊(s, a) = ζ(s, a) + ζ(s, 1 − a) and ζ₋(s, a) = ζ(s, a) − ζ(s, 1 − a) (symmetric and antisymmetric combinations of ζ(s, a) and ζ(s, 1 − a)), recently introduced in [19] for a ∈ ℝ. We prove that the functions w_α(X) = u_α(X) + iv_α(X), α > −1 are solutions of the Sturm-Liouville problem

()

for λ = 1. Here P_α(X) > 0, ρ_α(X) > 0, and Q_α(X) is a real function. The essential point consists in proving that the Wronskian of u_α(X) and v_α(X) is positive for all α > −1 and x ∈ ℝ. It allows one to prove that P_α(X) and ρ_α(X) are positive and to estimate the number of zeros of u_α(X) and v_α(X) on any bounded interval.

The fact that this Wronskian is positive also leads to a new inequality for the Hurwitz Zeta functions

()

where s > 1, z = 1/2 + iX/π, and the bar over the letter denotes complex conjugation. As far as we know, there are no results in the literature on the arguments of the Hurwitz Zeta functions. However, (1.4) provides some information on this issue. Indeed, setting

and

in (1.4) allows one to deduce the relation cos (φ_s+1(z) − φ_s(z)) > 0 for s > 1, z = 1/2 + iX/π, and X ∈ ℝ.

The paper is organized as follows. In Section 2, we provide the necessary information on the special functions involved. Section 3 is devoted to the study of Riesz potentials for KdV solitons and their Hilbert transforms. In Section 3.1, the main properties of these functions are summarized. Sturm-Liouville problem (1.2) is derived in Section 3.2. Section 3.3 deals with the properties of the Wronskian W[u_α, v_α]. Zeros of the functions u_α and v_α are studied in Section 3.4. In Section 4, the inequality (1.4) is discussed.

2. Preliminaries

Introduce the Fourier transform of the function f : ℝ → ℝ by

()

and the inverse Fourier transform by

()

For real α and x ∈ ℝ, define Riesz potentials of a function f(x) by the formula (see [7, page 117])

()

provided that the integral in the right-hand side exists. Define derivatives of

with respect to α by

()

provided that these integrals exist.

Introduce the Hilbert transform of the function f by (see [20, page 120])

()

where x ∈ ℝ and P.V. denotes the Cauchy principal value of the integral. According to our choice of the Fourier transform

, one can see that H² = −I on L_p(ℝ), p ≥ 1, where I is the identity operator. Also, ∂_x = H∘D and

, where the operator D is defined by (2.3).

Next, introduce the Trigamma function by (see [21, page 260, 6.4.1])

()

Notice that (see [21], page 260, 6.4.7)

()

Also, the following asymptotic expansion holds:

()

The Hurwitz (generalized) Zeta function is defined by (see [22, page 88])

()

This implies that

()

This function has the integral representation

()

where Γ(x) is the Gamma function. In two particular cases, we have (see [22]) that

()

where ζ(s) is the Riemann Zeta function.

The singularity of ζ(s, a) as s → 1 is given by the relation

()

The asymptotic expansion of ζ(s, a) for large a is (see [23])

()

where B_n are the Bernoulli numbers.

Introduce the full-range forms of Hurwitz Zeta functions (see [19])

()

Representations (2.16) and (2.17) imply that

()

Hence, follow the symmetric and antisymmetric properties of the functions,

()

It follows from (2.16) that ζ₊(s, a) is a periodic function of a, with the unit period. It is even with respect to a = 0 and a = 1/2. The function ζ₋(s, a) is odd about a = 1/2 and ζ₋(s, 1/2) = 0. These functions satisfy the functional differential equations

()

Consider now that s ∈ ℝ and denote by

the complex conjugate of a. Then

. It implies that, for a = a₁ + ia₂,

()

In a similar way,

()

Denote by W[u, v] the Wronskian of the functions u(x) and v(x), that is, . For reader′s convenience, we present here [24, Theorem 5.3].

Theorem 2.1. Let p(t) > 0, q(t) be real valued and continuous for 0 ≤ t ≤ T. Let u and v be real valued solutions of the equation

()

satisfying the condition

()

Let N be the number of zeros of u(t) on [0, T]. Then

()

In conclusion of this section, we would like to quote an interesting result concerning integrals over the real axis (see [25]).

Theorem 2.2. For any integrable function f(x) and g(x) = x − c²/x with c = const ∈ ℝ,

()

Moreover, the above formula holds true if

()

where {b_j} is any sequence of positive constants, c_j are any real constants, and the series is convergent.

3. Fractional Derivatives of A KdV Soliton and Their Conjugates

In this section, we consider Riesz fractional derivatives of a KdV soliton and their Hilbert transforms and establish their properties. We notice that all the graphs were obtained with the Mathematica 6 software.

We take the soliton solution of (1.1) in the form u₀(X) = 2sech² X with X = x − 4t (see Figure 1) and introduce the function

()

where

()

Notice that the functions u_α(X) and v_α(X) form a conjugate pair (see [20, page 120]) since

()

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graph of the soliton u₀(X).

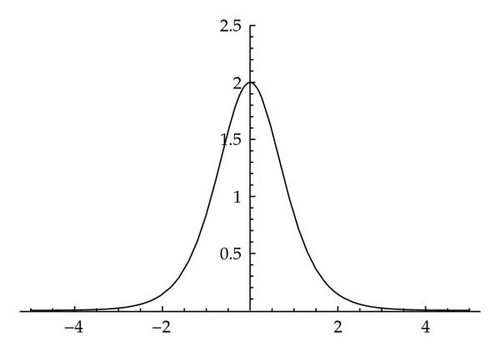
The next statement was proved in [15]. Using the functions (2.16) and (2.17), we rewrite it in a more convenient form.

Theorem 3.1. The functions u_α(X) and v_α(X) have the following representations for α > −1 and X ∈ ℝ:

()

where ζ₊(s, a) and ζ₋(s, a) are the full-range Hurwitz Zeta functions (see (2.16) and (2.17)) and Γ(s) is the Gamma function.

3.1. Properties of the Functions u_α and v_α

In this subsection, we collect the properties of the functions u_α and v_α. Some of them were established in [15] and some are given for the first time as follows.

Properties of the Functions uα and vα

(1) The functions u_α(X) and v_α(X) satisfy the functional differential equations

()

where α > −1, X ∈ ℝ, and the prime denotes differentiation with respect to X. This follows from (3.3) and the relation d/dX = H∘D.

(2) The functions u_α(X) are even and the functions v_α(X) are odd on ℝ (see [15] and Figures 1–4).
(3) The function u_α(X) is periodic with the period 𝒳 = iπ. It follows from the periodicity of ζ₊(s, a) with the unit period.
(4)
For all α > 0 (see [15]),

()

These properties are reflected on the graphs (see Figures 3 and 4).

(5)
For all α > 0 and n ∈ ℕ,

()

These relations follow from the differentiation of the identities in (3.7).

(6)
For all α > 0 and c ∈ ℝ,

()

Moreover,

()

where b_j is any sequence of positive constants, c_j are any real constants, and the series converges. These relations follow from (3.7) and Theorem 2.2.

(7)
The functional sequence of Riesz potentials {u_α(X)} converges pointwise to the soliton u₀(X), and the functional sequence {v_α(X)} converges pointwise to the conjugate soliton v₀(X) for α → 0⁺ (see [15]). Notice that

()

(see Figures 1 and 2). Here the conjugate soliton v₀(X) is given by

()

Equation (3.12) can be recovered from (3.5) with α = 0 thanks to (2.13).

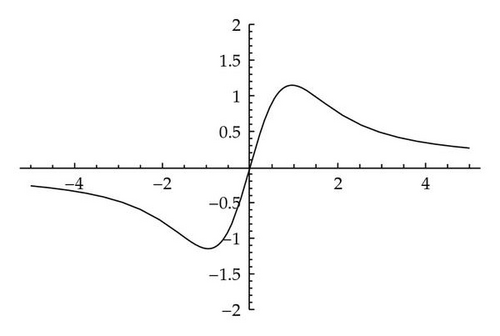
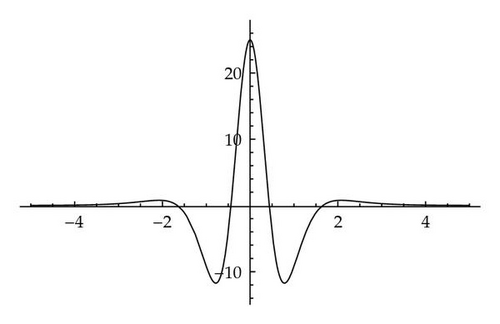
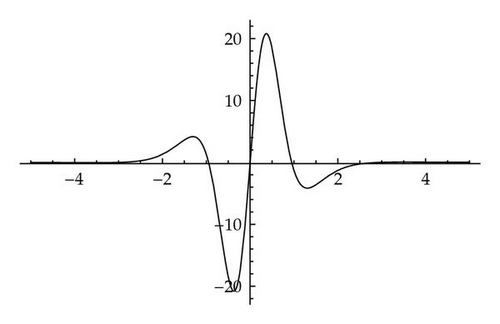
Remark 3.2. The conjugate soliton (3.12) is an algebraic solitary wave for extended KdV:

()

obtained by applying the Hilbert transform to (1.1) and setting v = −Hu. The term “algebraic solitary wave” is explained by the fact that v₀(X) has a 1/X decay for large X. More precisely (see [15]),

()

(8)
For α ≥ 0, the functions u_α and v_α are the elements of L₂(ℝ). Moreover, they are orthogonal in the principal value sense, namely, for all α₁, α₂ ≥ 0,

()

Equations (3.12) and (3.14) imply that v₀ ∈ L₂(ℝ). The fact that u_α and v_α with α > 0 are the elements of L₂(ℝ) follows from their asymptotics obtained in [15], namely,

()

Orthogonality of u_α and v_α follows from the fact that all u_α(X) with α ≥ 0 are even functions and all v_α(X) with α ≥ 0 are odd functions of X (see Property 2 and Figures 1–4).

(9)
At the point X = 0, one has for all α > −1

()

where ζ(s) is the Riemann Zeta function (see [15]).

3.2. Sturm-Liouville Problem

It is convenient to represent w_α(X) in the exponential form, namely,

()

where

()

Exponential representation (3.19) allows one to deduce the boundary value problem for the functions w_α(X). It turns out that for all α > −1 the functions w_α(X) solve the equation

()

where

()

Here W[u_α(X), v_α(X)] is the Wronskian of u_α(X) and v_α(X). Below we shall use a shorter notation W_α(X) = W[u_α(X), v_α(X)].

Taking into account the behavior of w_α(X) for large X (see [15]), we can restate the obtained results in another form. Indeed, w_α(X) are solutions of the Sturm-Liouville problem

()

corresponding to λ = 1. Without loss of generality, we can choose the constant in (3.22) to be positive. In the next subsection, we shall prove that W_α(X) > 0. It implies that P_α(X) > 0 and ρ_α(X) > 0 in (3.22).

It follows from (3.7) that for α > 0 the functions w_α(X) also satisfy the zero mean condition

()

This reflects the oscillatory behavior of w_α(X) for α > 0 (see Figures 3 and 4).

The graph of the arctangent function Φ_α(X) is shown in Figure 5. Φ_α(X) conveniently serves as a zero counter for both functions: u_α(X) and v_α(X). It possesses zeros at the points where v_α(X) has zeros and has jumps at the points where u_α(X) has zeros.

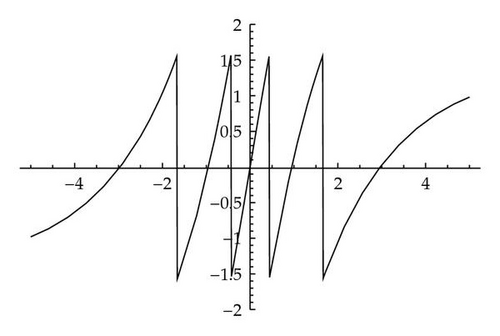
Remark 3.3. Observe that a general solution of (3.24) can be written in the form

()

where C₁, C₂ = const.

Remark 3.4. We would like to point out that the differential equation given by (3.21) can be factored in the following way (see [26, page 269]):

()

3.3. Wronskian of u_α and v_α

Lemma 3.5. The following properties hold for the Wronskian W_α(X) for α > −1 and all x ∈ ℝ:

()

Proof. We start with (3.29). Taking into account relations in (3.3) and the fact that ∂_X = H∘D, we can write

()

Since the functions u_α(X) are even and v_α(X) are odd with respect to X ∈ ℝ, W_α(X) is even for X ∈ ℝ. Differentiation of (3.31) with the help of (3.6) and (3.18) yields

. Next, we turn to the proof of (3.30). Since the functions u_α(X) and v_α(X) are linearly independent solutions of the equation (3.24), W_α(X)≠0 for all α > −1 and x ∈ ℝ. It remains to establish the sign of the Wronskian. In view of (3.17) and (3.18),

()

By Abel′s formula, for all X ∈ ℝ,

()

where the function

()

is continuous on ℝ. After some simplification, we have that

()

This representation yields (3.30). The lemma is proved.

Three-dimensional graph of W_α(X) is given in Figure 6.

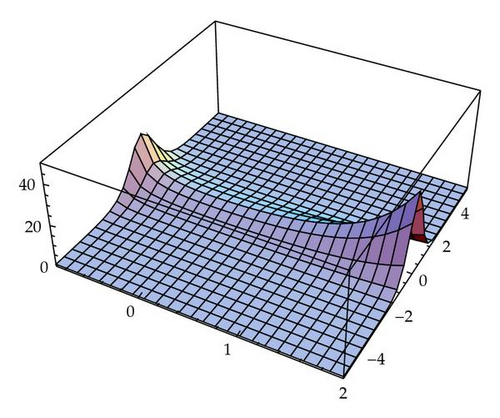
Remark 3.6. What does the positivity of the Wronskian yield for the soliton and its conjugate? For α = 0, (3.30) simplifies to read

()

We notice that v₀(X) > 0 for X > 0, v₀(−X) = −v₀(X) for X ∈ ℝ, and v₀(0) = 0 (see Figure 2). Integrating the inequality

over the interval [ε, X] for X ≥ ε > 0 and the inequality

over [−ε, X] for X ≤ −ε < 0 yields the estimate

()

3.4. Zeros of the Functions u_α(X) and v_α(X)

This subsection is devoted to the estimates of the number of zeros for the functions in question. By a strictly monotone change of variable

()

Equation (3.21) can be reduced to the equation

()

where 𝒲(y) = w(X(y)) and

. Therefore, any nontrivial solution of (3.39) can have not more than a finite number of zeros on any bounded interval ([24], page 323).

Theorem 3.7. Let N_α be the number of zeros of the function v_α(X) on the interval [0, X₀], where X₀ < ∞. Then the following inequality holds:

()

where

()

Proof. Since we chose C = 1 in (3.22),

()

Therefore,

()

Therefore, by Theorem 2.1 of Section 2, for the interval [0, X₀] we have the estimate

()

where

()

Here we have used the fact that ζ₋(s, 1/2) = 0 for s > 1.

Theorem 3.8. The zeros of u_α(X) separate and are separated by those of v_α(X).

Proof. This follows from Sturm′s Separation Theorem (see [24], page 335).

4. Inequality for Hurwitz Zeta Functions

Here we discuss a new inequality for the Hurwitz Zeta functions which follows from Lemma 3.5. The next statement is a corollary of this lemma.

Corollary 4.1. For s > 1 and z = 1/2 + iX/π with X ∈ ℝ, the following inequality holds:

()

This inequality can also be written in another form:

()

Proof. Dropping positive terms in front of the full-range Hurwitz Zeta functions in (3.4) and (3.5) and using (3.30) lead to

()

Remark 4.2. Setting and , we can rewrite (4.1) in the form

()

It shows that, for z = 1/2 + iX/π, X ∈ ℝ,

()

Introduce the scalar product for the complex-valued functions f = f₁ + if₂ and g = g₁ + ig₂ by the formula

()

Then for s > 1 and z = 1/2 + iX/π,

()

Remark 4.3. The proof of (4.1) becomes quite difficult when one approaches it from the point of view of special functions. For example, the use of integral representations (2.21) and (2.22) yields

()

The change of variables ξ = (t − τ)/2, η = (t + τ)/2 leads to

()

It is not clear at all that the integral (4.9) is positive for all s > 1 and X ∈ ℝ. However, (4.1) shows that it is. Multiplication of the series representations (2.16) and (2.17) does not make the proof any easier.

References

1 R. Hilfer, Applications of Fractional Calculus in Physics, 2000, World Scientific, River Edge, NJ, USA, MR1890104.
10.1142/3779
Google Scholar
2 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, 204, Elsevier Science, Amsterdam, The Netherlands, North-Holland Mathematics Studies, MR2218073.
10.1016/S0304-0208(06)80001-0
Google Scholar
3 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, MR1658022.
Web of Science® Google Scholar
4 Podlubny I., Geometric and physical interpretation of fractional integration and fractional differentiation, Fractional Calculus & Applied Analysis. (2002) 5, no. 4, 367–386, MR1967839, ZBL1042.26003.
Google Scholar
5 Luchko Y., Maximum principle for the generalized time-fractional diffusion equation, Journal of Mathematical Analysis and Applications. (2009) 351, no. 1, 218–223, https://doi.org/10.1016/j.jmaa.2008.10.018, MR2472935, ZBL1172.35341.
10.1016/j.jmaa.2008.10.018
Web of Science® Google Scholar
6 Duoandikoetxia J., Fourier Analysis, 2001, American Mathematical Society, Providence, RI, USA.
Google Scholar
7 Stein E. M., Singular Integrals and Differentiability Properties of Functions, 1970, Princeton University Press, Princeton, NJ, USA, Princeton Mathematical Series, no. 30, MR0290095.
Google Scholar
8 Kato T., On the Cauchy problem for the (generalized) Korteweg-de Vries equation, Studies in Applied Mathematics, 1983, 8, Academic Press, New York, NY, USA, 93–128, Advances in Mathematics. Supplementary Studies, MR759907, ZBL0549.34001.
Web of Science® Google Scholar
9 Kenig C. E., Ponce G., and Vega L., On the (generalized) Korteweg-de Vries equation, Duke Mathematical Journal. (1989) 59, no. 3, 585–610, https://doi.org/10.1215/S0012-7094-89-05927-9, MR1046740, ZBL0795.35105.
10.1215/S0012-7094-89-05927-9
Web of Science® Google Scholar
10 Kenig C. E., Ponce G., and Vega L., Well-posedness and scattering results for the generalized Korteweg-de Vries equation via the contraction principle, Communications on Pure and Applied Mathematics. (1993) 46, no. 4, 527–620, https://doi.org/10.1002/cpa.3160460405, MR1211741, ZBL0808.35128.
10.1002/cpa.3160460405
Web of Science® Google Scholar
11 Saut J. C. and Temam R., Remarks on the Korteweg-de Vries equation, Israel Journal of Mathematics. (1976) 24, no. 1, 78–87, MR0454425, https://doi.org/10.1007/BF02761431, ZBL0334.35062.
10.1007/BF02761431
Web of Science® Google Scholar
12 Varlamov V., Semi-integer derivatives of the Airy functions and related properties of the Korteweg-de Vries-type equations, Zeitschrift für Angewandte Mathematik und Physik. (2008) 59, no. 3, 381–399, https://doi.org/10.1007/s00033-007-6074-2, MR2399346, ZBL1155.35008.
10.1007/s00033-007-6074-2
Web of Science® Google Scholar
13 Varlamov V., Fractional derivatives of products of Airy functions, Journal of Mathematical Analysis and Applications. (2008) 337, no. 1, 667–685, https://doi.org/10.1016/j.jmaa.2007.03.098, MR2356101, ZBL1141.33002.
10.1016/j.jmaa.2007.03.098
Web of Science® Google Scholar
14 Varlamov V., Differential and integral relations involving fractional derivatives of Airy functions and applications, Journal of Mathematical Analysis and Applications. (2008) 348, no. 1, 101–115, https://doi.org/10.1016/j.jmaa.2008.06.052, MR2449330, ZBL1155.33005.
10.1016/j.jmaa.2008.06.052
Web of Science® Google Scholar
15 Varlamov V., Riesz potentials for Korteweg-deVries solitons, Zeitschrift für Angewandte Mathematik und Physik. In press.
Google Scholar
16 Sharpley R. C. and Vatchev V., Analysis of the intrinsic mode functions, Constructive Approximation. (2006) 24, no. 1, 17–47, https://doi.org/10.1007/s00365-005-0603-z, MR2217524, ZBL1100.94006.
10.1007/s00365-005-0603-z
Web of Science® Google Scholar
17 Vatchev V. and Sharpley R., Decomposition of functions into pairs of intrinsic mode functions, Proceedings of the Royal Society A. (2008) 464, no. 2097, 2265–2280, https://doi.org/10.1098/rspa.2007.0333, MR2429545.
10.1098/rspa.2007.0333
Google Scholar
18 Vallée O. and Soares M., Airy Functions and Applications to Physics, 2004, Imperial College Press, London, UK, MR2114198.
10.1142/p345
Google Scholar
19 McPhedran R. C., Botten L. C., Nicorovici N.-A. P., and Zucker I. J., Symmetrization of the Hurwitz zeta function and Dirichlet L functions, Proceedings of the Royal Society A. (2007) 463, no. 2077, 281–301, https://doi.org/10.1098/rspa.2006.1762, MR2281721, ZBL1151.11342.
10.1098/rspa.2006.1762
Google Scholar
20 Titchmarsh E. C., Introduction to the Theory of Fourier Integrals, 1962, 2nd edition, Oxford University Press, Glasgow, UK.
Google Scholar
21 M. Abramowitz and I. Stegun, Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, 1964, National Bureau of Standards, Washington, DC, USA.
Web of Science® Google Scholar
22 Srivastava H. M. and Choi J., Series Associated with the Zeta and Related Functions, 2001, Kluwer Academic Publishers, Dordrecht, The Netherlands, MR1849375.
10.1007/978-94-015-9672-5
Google Scholar
23 Magnus W., Oberhettinger F., and Soni R. P., Formulas and Theorems for the Special Functions of Mathematical Physics, 1966, Springer, New York, NY, USA, Die Grundlehren der Mathematischen Wissenschaften, Band 52, MR0232968.
10.1007/978-3-662-11761-3
Google Scholar
24 Hartman P., Ordinary Differential Equations, 1973, John Wiley & Sons, Baltimore, Md, USA, MR0344555.
Google Scholar
25 Glasser M. L., A remarkable property of definite integrals, Mathematics of Computation. (1983) 40, no. 162, 561–563, https://doi.org/10.2307/2007531, MR689471, ZBL0517.26008.
10.1090/S0025-5718-1983-0689471-1
Web of Science® Google Scholar
26 Zwillinger D., Handbook of Differential Equations, 1998, Academic Press, New York, NY, USA.
Google Scholar

Citing Literature

All articles

Riesz Potentials for Korteweg-de Vries Solitons and Sturm-Liouville Problems

Abstract

1. Introduction

2. Preliminaries

3. Fractional Derivatives of A KdV Soliton and Their Conjugates

3.1. Properties of the Functions u_α and v_α

3.2. Sturm-Liouville Problem

3.3. Wronskian of u_α and v_α

3.4. Zeros of the Functions u_α(X) and v_α(X)

4. Inequality for Hurwitz Zeta Functions

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Riesz Potentials for Korteweg-de Vries Solitons and Sturm-Liouville Problems

Abstract

1. Introduction

2. Preliminaries

3. Fractional Derivatives of A KdV Soliton and Their Conjugates

3.1. Properties of the Functions uα and vα

3.2. Sturm-Liouville Problem

3.3. Wronskian of uα and vα

3.4. Zeros of the Functions uα(X) and vα(X)

4. Inequality for Hurwitz Zeta Functions

References

Citing Literature

Figures

References

Related

Information

3.1. Properties of the Functions u_α and v_α

3.3. Wronskian of u_α and v_α

3.4. Zeros of the Functions u_α(X) and v_α(X)