We study spectral properties of a family of quasiperiodic Schrödinger operators on the real line in the adiabatic limit. We assume that the adiabatic iso-energetic curve has a real branch that is extended along the momentum direction. In the energy intervals where this happens, we obtain an asymptotic formula for the Lyapunov exponent and show that the spectrum is purely singular. This result was conjectured and proved in a particular case by Fedotov and Klopp (2005).

1. Introduction

We consider the following Schrödinger equation:

()

where x ↦ V(x) is 1-periodic, ζ ↦ W(ζ) is 2π-periodic, and ε small is chosen so that the potential V(·−z) + W(ε·) be quasi-periodic. Note that in this case, the family of equations (1.1) is ergodic; see [1]; so its spectrum does not depend on z; see [2]. The operator H_z,ε can be regarded as an adiabatic perturbation of the periodic operator H₀:

()

Equation (1.1) is one of the main models of solid state physics. The function ψ is the wave function of an electron in a crystal with an external electric field. V represents the potential of the perfect crystal; as such it is periodic. The potential W represents an external electric field. In the semiconductors, this perturbation is slow-varying with respect to the field of the crystal, [3]. It is natural to consider the semiclassical limit.

The Iso-Energy Curve Let ℰ(κ) be the dispersion relation associated to H₀. Consider the complex and real-isoenergy curves Γ_ℂ and Γ_ℝ defined by

()

Notice that the iso-energy curves Γ_ℂ(E) and Γ_ℝ(E) are 2π-periodic in ζ and κ and Γ_ℂ is the Riemann surface uniformizing κ.

The real iso-energy curve has a well-known role for adiabatic problems [4]. The adiabatic limit can be regarded as a “semiclassical” limit and the Hamiltonian ℰ(κ) + W(ζ) can be interpreted as a “classical” Hamiltonian corresponding to (1.1).

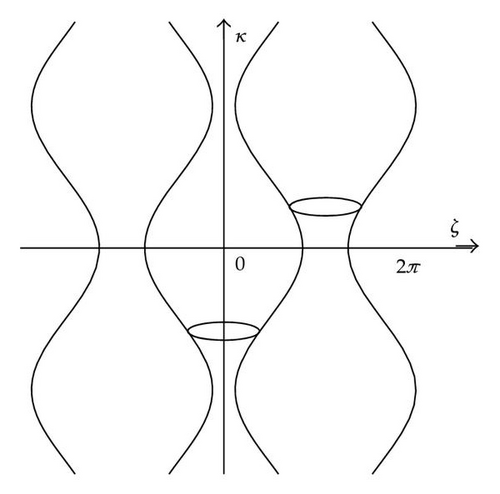
In the case when the interval E − W(ℝ) contains one spectral band (we refer to that by “isolated band” model), the iso-energy curve is presented in Figure 1. The real branches are vertical curves, they are connected by complex loops (closed curves) lying on Γ_ℂ; loops are represented by horizontal closed curves. In this case the connected components are extended in κ-direction and bounded in ζ-direction.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The iso-energy curve for “isolated band” model.

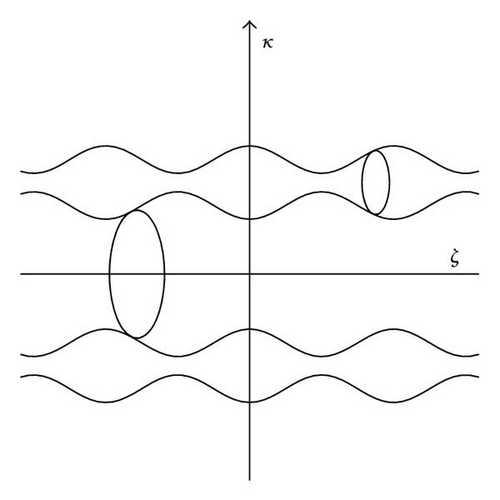
In the case when the interval E − W(ℝ) is contained in a spectral band (we refer to that by the “band middle” model), the iso-energy curve is presented in Figure 2. The horizontal curves are connected components of Γ_ℝ; the vertical loops are situated in Γ_ℂ. In this case the connected components are bounded in κ direction and extended in ζ-direction.

When W has in a period exactly one maximum and one minimum, that are nondegenerate, it is proved in [5] that in the energy intervals where the adiabatic iso-energetic curves are extended along the momentum direction, the spectrum is purely singular. This result leads to the following conjecture: in a given interval, if the iso-energy curve has a real branch (a connected component of the real iso-energy curve Γ_ℝ, see Figure 1 and [5]) that is an unbounded vertical curve, then in the adiabatic limit, in this interval, the spectrum is singular. This paper is devoted to prove this conjecture.

Heuristically when the real iso-energy curve is extended along the momentum axis, the quantum states should be extended in momentum and thus localized in the position space.

1.1. Results and Discussions

Now, we state our assumptions and results.

1.1.1. Assumptions on the Potentials

We assume the following.

(H1) V and W are periodic:
()
(H2) V is real-valued and locally square-integrable.
(H3) W is real analytic in the strip S_Y = {z ∈ ℂ; | Im z | < Y}.

We define

()

We define the spectral window 𝒲(E) by

()

1.1.2. Assumptions on the Energy Region

To describe the energy regions where we study the spectral properties, we consider the periodic Schrödinger operator H₀ acting on L²(ℝ) and defined by (1.2).

1.1.3. The Periodic Operator

The spectrum of (1.2) is absolutely continuous and consists of intervals of the real axis, say [E_2n+1, E_2n+2] for n ∈ ℕ, such that E₁ < E₂ ≤ E₃ < E₄, …, E_2n ≤ E_2n+1 < E_2n+2, … and E_n → +∞, n → +∞. The points (E_j) _j∈ℕ are the eigenvalues of the self-adjoint operator obtained by considering H₀ defined by (1.2) and acting in L²([0,2]) with periodic boundary conditions (see [6, 7]). The intervals [E_2n+1, E_2n+2], n ∈ ℕ, are the spectral bands, and the intervals (E_2n, E_2n+1), n ∈ ℕ^*, the spectral gaps. When E_2n < E_2n+1, one says that the nth gap is open; when [E_2n−1, E_2n] is separated from the rest of the spectrum by open gaps, the nth band is said to be isolated. The spectral bands and gaps are represented in Figure 4.

1.1.4. The Geometric Assumption

Let us describe the energy region where we study (1.1). We assume that J is a real compact interval such that, for all E ∈ J, the window 𝒲(E) contains exactly N ≥ 1 isolated bands of the periodic operator. So, we fix two positive integers n and N > 0 and assume that:

(H4a) The bands [E_2(n+j)−1, E_2(n+j)], j = 1,2, …, N, are isolated.
(H4b) For all E ∈ J, these bands are contained in the interior of 𝒲(E).
(H4c) For all E ∈ J, the rest of the spectrum of H₀ is outside of 𝒲(E).

Remark 1.1. The geometric assumption assures that the iso-energy curve Γ_ℝ(E) contains a real branch that is an unbounded vertical curve.

We asked that the window contains only isolated bands of the periodic operator to have a control on the branch points of the Bloch quasimomentum and on its properties of analyticities.

1.1.5. The Main Result

The main object of this paper is to prove the following.

Theorem 1.2. Let J be a real compact interval. We assume that (H1)–(H4) are satisfied. For ε > 0 sufficiently small, for almost all z ∈ ℝ, one has

()

Here σ_ac(H_z,ε) is the absolutely continuous spectrum of the family of (H_z,ε).

Remark 1.3. (1) It is proved in [8] that for Σ = σ(H₀) + W(ℝ) = σ(H₀) + [W₋, W₊], one has the following for all ε ≥ 0, σ(H_z,ε) ⊂ Σ, and for any K ⊂ Σ, compact, there exists C > 0 such that for all ε sufficiently small and all E ∈ K,

()

So, for an interval J as in Theorem 1.2, we have

()

(2) Using the Ishii-Pastur-Kotani Theorem [1, 9], one can see that the result of Theorem 1.2 is deduced from the positivity of the Lyapunov exponent. This will be done by computing the asymptotics for the Lyapunov exponent. With the aim of simplifying the introduction, we do not give it here; it is the subject of Section 3.1.

2. Periodic Schrödinger Operators

This section is devoted to the study of the periodic Schrödinger operator (1.2) where V is a 1-periodic, real-valued, - function. We recall known facts needed on the present paper and we introduce notations. Basic references are [6, 10–12].

2.1. Geometric Description

2.1.1. The Set W⁻¹(ℝ)

As E ∈ ℝ, the set (E − W) ⁻¹(ℝ) coincides with W⁻¹(ℝ). It is 2π-periodic. It consists of the real line and of complex branches (curves) which are symmetric with respect to the real line. There are complex branches beginning at the real extrema of W that do not cross again the real line.

Consider an extremum of W of order n_i on the real line, say ζ_i. Near ζ_i, the set W⁻¹(ℝ) consists of a real segment and of n_i − 1 complex curves symmetric with respect to the real axis and intersecting the real axis only on ζ_i. The angle between two neighboring curves is equal to π/n_i. Let Y > 0. We set S_Y = {−Y ≤ Im ζ ≤ Y}. We assume that Y is so small that

(i)
S_Y is contained in the domain of analyticity of W;
(ii)
the set W⁻¹(ℝ)∩S_Y consists of the real line and of the complex lines passing through the real extrema of W.

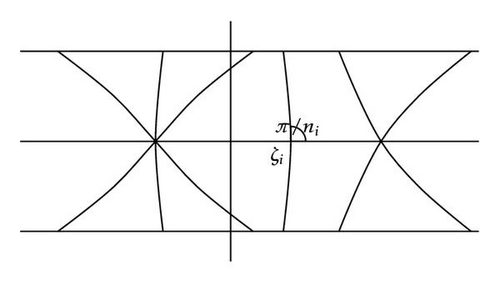
An example of subset W⁻¹(ℝ) is shown in Figure 3.

2.1.2. Notations and Description of (E − W) ⁻¹(σ(H₀))

For all E ∈ J, we write

()

with the following properties.

(i)
(ii)
As we deal with the case when the iso-energy curve has a real branch that is extended along the momentum direction, without loss of generality we consider that the connected component is associated to a connected component of Γ_ℝ(E) which is an unbounded vertical curve. See Remark 2.3.
(iii)
We generally define the following

()

We set ℬ_j(E) =

and 𝒢_N(E) =

Let

be the extrema of W in 𝒢_j. We recall that

is the order of

We have the following description.

Lemma 2.1. Fix [A, B] a compact interval of ℝ.

There exists a finite number p of real extrema of W in [A, B].

(i) If p = 0, there exists Y > 0 such that

()

(ii) For p > 0, one denotes by {ζ₁, …, ζ_p} the real extrema of W in [A, B]. There exists Y > 0 and a sequence of disjoint and strictly vertical lines of ℂ₊ starting at ζ_i such that

()

2.2. Bloch Solutions

Let ψ be a solution of the equation

()

satisfying the relation

()

for all x ∈ ℝ and some nonvanishing complex number λ(ℰ) independent of x. Such a solution exists and is called the Bloch solution and λ(ℰ) is called Floquet multiplier. We discuss its analytic properties as a function of ℰ.

As in Section 1.1.2, we denote the spectral bands of the periodic Schrödinger operator by [E_2n+1, E_2n+2], n ∈ ℕ. Consider 𝒮_± two copies of the complex plane ℰ ∈ ℂ cut along the spectral bands. Paste them together to get a Riemann surface with square root branch points. We denote this Riemann surface by 𝒮.

One can construct a Bloch solution ψ(x, ℰ) meromorphic on 𝒮. It is normalized by the condition ψ(1, ℰ) ≡ 1. The poles of this solution are located in the open spectral gaps or at their edges; the closure of each spectral gap contains exactly one pole that, moreover, is simple. It is located either on 𝒮₊ or on 𝒮₋. The position of the pole is independent of x.

For ℰ ∈ 𝒮, we denote by

the point on 𝒮 different from ℰ and having the same projection on ℂ as ℰ. We let

()

The function

is another Bloch solution of (2.5). Except at the edges of the spectrum, the functions ψ and

are linearly independent solutions of (2.5). In the spectral gaps, ψ and

are real-valued functions of x, and, on the spectral bands, they differ only by complex conjugation.

2.3. The Bloch Quasimomentum

Consider the Bloch solution ψ(x, ℰ). The corresponding Floquet multiplier λ(ℰ) is analytic on 𝒮. Represent it in the form λ(ℰ) = exp (ik(ℰ)). The function ℰ ↦ k(ℰ) is the Bloch Quasimomentum of H₀. Its inverse k ↦ E(k) is the dispersion relation of H₀. A branching point ζ is a point where k^′(ζ) = 0.

Let D be a simply connected domain containing no branch point of the Bloch Quasimomentum. In D, one can fix an analytic single-valued branch of k, say k₀. All the other single-valued branches of k that are analytic in D are related to k₀ by the following formulae:

()

Consider ℂ₊, the upper half plane of the complex plane. On ℂ₊, one can fix a single-valued analytic branch of the Quasimomentum continuous up to the real line. It can be determined uniquely by the conditions Rek(ℰ + i0) = 0 and Im k(ℰ + i0) > 0 for ℰ < E₁. We call this branch the main branch of the Bloch Quasimomentum and denote it by k_p.

The function k_p conformally maps ℂ₊ onto the first quadrant of the complex plane cut at compact vertical slits starting at the points πl, l ∈ ℕ. It is monotonically increasing along the spectral zones so that [E_2n−1, E_2n], the nth spectral band, is mapped on the interval [π(n − 1), πn]. Along any open gap, Rek_p(ℰ + i0) is constant, and Im k_p(ℰ + i0) is positive and has only one nondegenerate maximum.

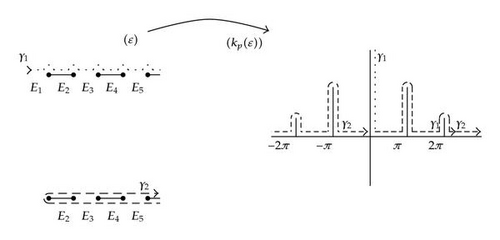
Consider ℂ₀, the complex plane cut along the spectral the real line from E₁ to +∞. In Figure 4, we drew two curves in ℂ₀ and their images under the transformation ℰ ↦ k_p(ℰ).

All the branch points of k_p are of square root type. Let E_l be a branch point of k_p. In a sufficiently small neighborhood of E_l, the function k_p is analytic in

, and

()

Finally, we note that the main branch can be continued analytically to the complex plane cut along (−∞, E₁] and the spectral gaps ]E_2n, E_2n+1[, n ∈ ℕ^*, of the periodic operator H₀.

2.4. A Meromorphic Function

Now let us discuss a function playing an important role in the adiabatic constructions.

In [10], it is shown that, on 𝒮, there is a meromorphic function ω having the following properties:

(i)
the differential Ω = ωdℰ is meromorphic; its poles are the points of P ∪ Q, where P is the set of poles of ℰ ↦ ψ(x, ℰ), and Q is the set of zeros of k^′;
(ii)
all the poles of Ω are simple;
(iii)
if the residue of Ω at a point p is denoted by res_pΩ, one has
()
(iv)
if ℰ ∈ 𝒮 projects into a gap, then ω(ℰ) ∈ ℝ.
(v)
if ℰ ∈ 𝒮 projects inside a band, then

2.4.1. The Complex Momentum

It is the main analytic object of the complex WKB method. Let ζ ∈ S_Y. We define κ, in 𝒟(W) the domain of analyticity of W, by

()

Here, k is the Bloch Quasimomentum defined in Section 2.3. Though κ depends on E, we omit the E-dependence. Relation (2.11) translates the properties of k into properties of κ. Hence, ζ ↦ κ(ζ) is a multivalued analytic function, and its branch points are related to the branch points of the Quasimomentum by the relations

()

Let ζ₀ be a branch point of κ. If W′(ζ₀) ≠ 0, then ζ₀ is a branch point of square root type.

If D ⊂ 𝒟(W) is a simply connected set containing no branch points of κ, we call it regular. Let κ_p be a branch of the complex momentum analytic in a regular domain D. All the other branches that are analytic in D are described by the following formulae:

()

Here ± and m ∈ ℤ are indexing the branches.

2.4.2. Index of an Interval

Fix j ∈ {1, …, N}. Fix a continuous branch κ_j of the complex momentum on

We define

()

p_j is the index of

associated to κ_j.

Let us give some properties of p_j.

Lemma 2.2. Assume that (H4) is satisfied. The indices p_j have the following properties.

(1)
For j ∈ {1, …, N}, p_j ∈ {−1,0, 1}.
(2)

Proof. The points and are the ends of a band of σ(H₀): they are distinct or coincide. If they coincide, that is, if the index p_j satisfies p_j = 0. Else, we consider k_j the branch of the Quasimomentum associated to κ_j. We have that

()

see (2.8), and |p_j| = 1.

Let us prove point (2).As for any j ∈ {1, …, N}, we have |p_j| = p_jmod 2. We write

()

For j ∈ {1, …, N − 1},

and

are the ends of a same gap and

()

By periodicity,

and

are the ends of the same gap.

This ends the proof of Lemma 2.2.

If p_j ≠ 0, we say that we cross a band. In this case, and the associated connected component of the iso-energy curve is unbounded vertically.

We notice that p₁ ≠ 0, and thus .

Remark 2.3. We can choose the determination of κ such that p₁ = 1.

2.4.3. Tunneling Coefficients

For j ∈ {1, …, N}, we denote by γ_j a smooth closed curve that goes once around

. Notice that this curve is the projection of a closed curve on the complex Riemann surface κ(ζ) = k(E − W(ζ)). We consider the tunneling actions S_j given by

()

It is straightforward to prove that for E ∈ J, each of these actions is real and nonzero and that S_j(E) is analytic in a complex neighborhood of J (for analogous statements, we refer to [13, 14]). By definition, we choose the direction of the integration so that all the tunneling actions is positive. We set

()

S_j(E) is called the tunneling action; we choose the branch κ so that on J, S_j(E) is positive. We define

()

So we get

()

S_j(E) being positive we get that T is exponentially small. For more details on the properties of tunneling coefficients, see [5, Section 10].

3. The Proof of Theorem 1.2

3.1. The Asymptotics of the Lyapunov Exponent

3.1.1. Spectral Results

One of the main objects of the spectral theory of quasi-periodic operators is the Lyapunov exponent (for a definition and additional information, see, e.g., [9]). The main result of this section is as follows.

Theorem 3.1. We assume that the assumptions (H1)–(H4) are satisfied. Then, on the interval J, for sufficiently small irrational ε/2π, the Lyapunov exponent Θ(E, ε) of (1.1) is positive and satisfies the asymptotics

()

This theorem implies that if ε/2π is sufficiently small and irrational, then, the Lyapunov exponent is positive for all E ∈ J.

3.2. The Monodromy Matrix and the Lyapunov Exponents

The main object of our study in this subsection is the monodromy matrix for the family of (1.1), and we define it briefly (we refer the reader to [5, 13]). In this paper, we compute the asymptotics of its Fourier expansion in the adiabatic limit.

3.2.1. Definition of the Monodromy Matrix

Fix E ∈ ℝ. Consider the family of differential equations indexed by z ∈ ℝ:

()

Definition 3.2. We say that (ψ_i) _i∈{1,2} is a consistent basis of solutions to (3.2) if the two functions ((x, z) ↦ ψ_i(x, z, E)) _i∈{1,2} are a basis of solutions to (3.2) whose Wronskian is independent of z and that are 1-periodic in z, that is, that satisfy

()

We refer the reader to [5, 10] about the existence and details on consistent basis of solutions to (3.2).

The functions ((x, z) ↦ ψ_i(x + 2π/ε, z + 2π/ε, E)) _i∈{1,2} being also solutions of (3.2), we get the relation

()

where

(i)
(ii)
M(z, E) is a 2 × 2-matrix with coefficients independent of x.

The matrix M is called the monodromy matrix associated to the consistent basis (ψ_1,2). We recall the following properties of this matrix:

()

The Matrix M belongs to SL (2, ℝ) which is known to be isomorph to SU (1,1).

3.3. The Lyapunov Exponents and the Monodromy Equation

Consider now a 1-periodic, SL(2, ℂ)-valued function, say,

and h > 0 irrational. Consider the finite difference equation:

()

Going from (1.1) to the (3.6) is close to the monodromization transformation introduced in [8] to construct Bloch solutions of difference equation. Indeed, it appears that the behavior of solutions of (1.1) for x → ∓∞ repeats the behavior of solutions of the monodromy equation for n → ∓∞. And it is a well-known fact that the spectral properties of the one-dimensional Schrödinger equations can be described in terms of the behavior of its solutions as x → ∓∞.

The Lyapunov exponent of the finite difference equation (3.6) is

()

where the matrix cocycle (P_N(z, h)) _N∈ℕ is defined as

()

It is well known that if h is irrational, and

is sufficiently regular in z, then the limit (3.7) exists for almost all z and is independent of z.

Set h ≡ 2π/ε [2]. Let M be the monodromy matrix associated to a consistent basis (ψ_1,2). Consider the monodromy equation:

()

The Lyapunov exponent of the monodromy equation (3.9) is defined by

()

There are several deep relations between (3.2) and the monodromy equation (3.9) (see [5, 15]). We describe only one of them. Recall that Θ(E, ε) is the Lyapunov exponent of (1.1). We have the following result.

Theorem 3.3 (see [5].)Assume that ε/2π is irrational. The Lyapunov exponents Θ(E, ε) and θ(E, ε) are related by the following relation:

()

3.4. The Asymptotics of the Monodromy Matrix

As W and V are real on the real line, we construct a monodromy matrix of the following form:

()

To get (3.12), it suffices to consider a basis of solutions of the form

. The details on the existence and the construction of such a basis are developed in [13].

The following result gives the asymptotics of A and B in the adiabatic case.

Theorem 3.4. Let E₀ be in J. There exists Y > 0 and V₀, a neighborhood of E₀, such that, for sufficiently small ε, the family of (3.2) has a consistent basis of solutions for which the corresponding monodromy matrix M is analytic in (z, E)∈{z ∈ ℂ; | Im z | < Y/ε} × V₀ and has the form (3.12). When ε tends to 0, the coefficients A and B admit the asymptotics

()

The integers P₋, P₊ and Q₋, Q₊ ∈ ℤ are specified in Section 3. There exists a constant C > 1 such that for ε > 0 sufficiently small and E ∈ V₀∩ℝ, one has

()

where T(E, ε) is defined in (2.21).

For Y₁ and Y₂ such that 0 < Y₁ < Y₂ < Y, there exists V = V(Y₁, Y₂) a neighborhood of E₀ such that the asymptotics (3.13) and (3.14) for A and B are uniform in (z, E)∈{z ∈ ℂ; Y₁/ε<|Im z | < Y₂/ε} × V.

Remark 3.5. The coefficients A₊, A₋, B₊, and B₋ are the leading terms of the asymptotics of the Q_∓th and P_∓th Fourier coefficients of the monodromy matrix coefficients. From Theorem 3.4, one deduces that, in the strip {−Y < Im ζ < Y}, only a few Fourier series terms of the monodromy matrix dominate.

3.5. The Proof of Theorem 3.1

3.5.1. The Upper Bound

Fix P = max | P_∓ | , |Q_∓|. The asymptotics (3.13) and (3.14) and estimates (3.15) imply the following estimates for the coefficients of M(z, E), the monodromy matrix:

()

Here, C(y₀) is a positive constant independent of ε, Rez, and E. The estimates are valid for sufficiently small ε. We recall that M is analytic and 1-periodic in z. Equation (3.16) and the maximum principle imply that

()

This leads to the following upper bound for the Lyapunov exponent for the matrix cocycle generated by M(z, E):

()

where C is a constant independent of E and ε. Using (3.11) one gets

()

3.5.2. The Lower Bound

For (M(z, ε) _0<ε<1) a family of SL(2, ℂ)-valued, 1-periodic functions of z ∈ ℂ, and h an irrational number, we recall the following result obtained in [8].

Proposition 3.6. Fix ε₀ > 0. Assume that there exist y₀ and y₁ such that 0 < y₀ < y₁ < ∞ and such that, for any ε ∈ (0, ε₀), one has

(i)
the function z → M(z, ε) is analytic in the strip S = {z ∈ ℂ; 0 ≤ Im z ≤ y₁/ε};
(ii)
in the strip S₁ = {z ∈ ℂ; y₀/ε ≤ Im z ≤ y₁/ε} ⊂ S, M(z, ε) admits the representation
()
for some constant λ(ε), some integer n₀, and a matrix M₀(ε), all of them independent of z;
(iii)
(iv)
there exist constants β > 0 and α ∈ (0,1) independent of ε such that |α(ε)| ≤ α and |β(ε)| ≤ β;
(v)
as ε → 0.

Then, there exists C > 0 and ɛ₁ > 0 (both depending only on y₀, y₁, α, β, and ε ↦ m(ε)) such that, if 0 < ε < ε₁, one has

()

Proposition 3.6 is used by applying the arguments of [5, 10] to get the lower bound for the Lyapunov exponent.

First for we prove that the matrix σM(z, E)σ completes the assumption of Proposition 3.6.

Let y₀ and y₁ be fixed such that 0 < y₀ < y₁ < Y. The asymptotics of the monodromy matrix are uniform for z in S = {z ∈ ℂ; y₀/ε ≤ Im z ≤ y₁/ε} and E ∈ V₀.

Let us assume that n = N_N in (5.16) is even; then the following relations hold:

()

Equation (3.22) is derived from the expression of Q_± and P_±, given in Section 5.3.

are equals for 2 ≤ j ≤ N. The first expression of formula (3.22) deduced the relation between

and

(see (5.27) and (5.32)), the second one from the relation between

and

(see (5.21) and (5.32)), and the last one from the relation between

and

(see (5.17) and (5.32)). We notice that (3.22) depends only on the indices of 𝒢₁ because we constructed the consistent basis near

. See Section 4.4.

For E ∈ V₀∩ℝ and z ∈ S, Theorem 3.4 implies that

()

where c(E) is independent of z and bounded by a constant uniformly in ε and E. So, we have

()

This gives that the matrix-valued function

()

satisfies the assumptions of Proposition 3.6.

Remark 3.7. When n = N_N in (5.16) is odd, then we get

()

For E ∈ V₀∩ℝ and z ∈ S, Theorem 3.4 implies that

()

where c(E) is independent of z and bounded by a constant uniformly in ε and E. So, we have

()

The most important properties of the matrix M(z, E) in Proposition 3.6 are that the bigger eigenvalue is 1 [8].

Using (3.21), we get that the Lyapunov exponent θ(E, ε) of the matrix cocycle associated to (M(·, E), h) satisfies the estimates

()

Taking into account (1.2) we get that

()

By (3.15) we get

()

3.5.3. Conclusion

Now we obtain (3.1), by comparing (3.19) and (3.31). Indeed we see that

()

The expression of T(E) given by (3.32) and (3.31) gives (3.1) for any E ∈ V₀∩ℝ.

Recall that V₀∩ℝ is an open interval containing E₀ ∈ J. The above construction can be carried out for any E₀ ∈ J. The end of the proof of Theorem 1.2 follows from the compactness of the interval J.

4. The Complex WKB Method for Adiabatic Problems

In this section, following [10, 16, 17], we describe the complex WKB method for adiabatically perturbed periodic Schrödinger equations:

()

Here, V is 1-periodic and real valued, ε is a small positive parameter, and the energy E is complex; one assumes that V is

and that W is analytic in a strip in the neighborhood S_Y of the real line.

The parameter ζ is an auxiliary complex parameter used to decouple the slow variable ζ = εx and the fast variable x. The idea of this method is to study solutions of (4.1) in some domains of the complex plane of ζ and then to recover information on their behavior in x ∈ ℝ. Therefore, for D being a complex domain, one studies solutions satisfying the following condition:

()

The aim of the WKB method is to construct solutions to (4.1) satisfying (4.2) and that have simple asymptotic behavior when ɛ tends to 0. This is possible in certain special domains of the complex plane of ζ. These domains will depend continuously on V, W, and E. We will use these solutions to compute the monodromy matrix; we consider V and W as fixed and construct the WKB objects and solutions in a uniform way for energies near E.

4.1. Standard Behavior of Consistent Solutions

We start by defining another analytic object central to the complex WKB method, the canonical Bloch solutions. Then, we describe the standard behavior of the solutions.

4.1.1. Canonical Bloch Solutions

To describe the asymptotic formulae of the complex WKB method, one needs to construct Bloch solutions to the following equation

()

that are moreover analytic in ζ on a given regular domain.

Let ζ₀ be a regular point (i.e., ζ₀ is not a branch point of κ). Let ℰ₀ = ℰ(ζ₀). Assume that ℰ₀ ∉ P ∪ Q. Let U₀ be a sufficiently small neighborhood of ℰ₀, and let V₀ be a neighborhood of ζ₀ such that ℰ(V₀) ⊂ U₀. In U₀, we fix a branch of the function

and consider ψ_±(x, ℰ), the two branches of the Bloch solution ψ(x, ℰ) and Ω_±, and the corresponding branches of Ω (see Section 2.4.). For ζ ∈ V₀, we set

()

The functions Ψ_± are called the canonical Bloch solutions normalized at the point ζ₀.

The properties of the differential Ω imply that the solutions Ψ_± can be analytically continued from V₀ to any regular domain containing V₀.

The Wronskian of Ψ_± satisfies (see [13])

()

For ℰ₀ ∉ Q ∪ {E_l}, the Wronskian w(Ψ₊(·, ζ), Ψ₋(·, ζ)) is nonzero.

4.2. Solutions Having Standard Asymptotic Behavior

Fix E = E₀. Let D be a regular domain (i.e., D ⊂ D(W), and simply connected set containing no branch points of κ). Fix ζ₀ ∈ D so that ℰ(ζ₀) ∉ P ∪ Q. Let κ be a continuous branch of the complex momentum in D, and let Ψ_± be the canonical Bloch solutions normalized at ζ₀ defined on D and indexed so that κ is the Quasimomentum for Ψ₊.

Definition 4.1. Let σ ∈ {+, −}. We say that, in D, a consistent solution f has standard behavior (or standard asymptotics) if

(i)
there exists V₀, a complex neighborhood of E₀, and X > 0 such that f is defined and satisfies (4.1) and (4.2) for any (x, ζ, E)∈(−X, X) × D × V₀;
(ii)
f is analytic in ζ ∈ D and in E ∈ V₀;
(iii)
for any compact set K ⊂ D, there exists V ⊂ V₀, a neighborhood of E₀, such that, for (x, ζ, E)∈(−X, X) × K × V, f has the uniform asymptotic:
()
(iv)
this asymptotic can be differentiated once in x without loosing its uniformity properties. We set
()

We call ζ₀ the normalization point for f. To say that a consistent solution f has standard behavior, we will use the following notation:

()

4.3. Some Results on the Continuation of Asymptotics

4.3.1. Description of the Stokes Lines near

This section is devoted to the description of the Stokes lines under assumption (H4).

4.3.2. Definition

The definition of the Stokes lines is fairly standard [13, 15]. The integral ζ ↦ ∫^ζκ(u)du has the same branch points as the complex momentum. Let ζ₀ be one of them. Consider the curves beginning at ζ₀ and described by the following equation:

()

These curves are the Stokes lines beginning at ζ₀. According to (2.8), the Stokes line definition is independent of the choice of the branch of κ.

Assume that W^′(ζ₀) ≠ 0. Equation (2.9) implies that there are exactly three Stokes lines beginning at ζ₀. The angle between any two of them at this point is equal to 2π/3. Indeed for ζ near ζ₀, we have

()

4.3.3. Stokes Lines for E₀ ∈ J

We describe the Stokes lines beginning at and . Since W is real on ℝ, the set of the Stokes lines is symmetric with respect to the real line.

First, κ₁ is real on the interval ; therefore this set is a Stokes line starting at . The two other Stokes lines beginning at are symmetric with respect to the real axis. We denote by the Stokes line going downward and by its symmetric. Similarly, we denote by and the two other Stokes lines starting at , and goes upward. These Stokes lines are represented in Figure 5.

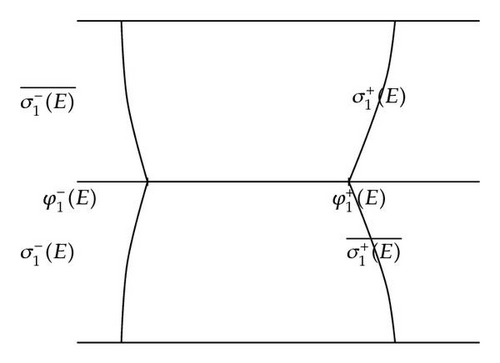
Lemma 4.2. The Stokes lines and satisfy the following properties.

(i)
The Stokes lines and stay vertical.
(ii)
and do not intersect one another.

The proof of this lemma is similar to the studies done in [5, 14, 17, 18]. We do not give the details.

4.4. Construction of a Consistent Basis near

We recall this result, proved in [17].

Proposition 4.3 (see [17].)Fix E₀ ∈ J, and let κ₁ be a continuous determination of the complex momentum on . There exists a real number Y > 0, a complex neighborhood 𝒱₁ of E₀, and a consistent basis (f₁, (f₁) ^*) of solutions of (4.1) such that f₁ has the standard asymptotic behavior:

()

to the left of

(resp., to the right of

). The determination

is the continuation of κ₁ through

(resp., through

We mimic the analysis done in [5, Section 5]. Precisely, we start by a local construction of the solution f using canonical domain; then, we apply continuation tools, that is, the rectangle lemma, the adjacent domain principle, and the Stokes Lemma.

5. The Proof of Theorem 3.4

The Proof of Theorem 3.4 follows the same ideas as the computations given in [5, Section 10.2]. Below we give the details for the proof of (3.13), (3.14), and (3.15).

5.1. Strategy of the Computation

We now begin with the construction of the consistent basis the monodromy matrix of which we compute. Recall that (H1)–(H4) are satisfied.

In the present section, we construct and study a solution f of (3.2) satisfying (3.3).

To use the complex WKB method, we perform the following change of variable in (3.2):

()

Then (3.2) takes the form (4.1). In the new variables, the consistency condition (3.3) becomes (4.2). Note also that in the new variables, for two solutions to (4.1) to form a consistent basis, in addition to being a basis of consistent solutions, their Wronskian has to be independent of ζ.

Consider the basis

constructed around

as in Proposition 4.3. Then the monodromy matrix associated to the basis

(defined in Section 3.2.1) satisfies

()

The aim of this section is the computation of M(ζ, E, ε). The definition of the monodromy matrix implies that

()

This gives that the monodromy matrix is analytic in ζ in the strip S_Y and in E in a constant neighborhood of E₀. By the definition of f₁ we get that A and B are ε-periodic in ζ ∈ S_Y. This is an immediate consequence of the properties of f₁.

Therefore, we will compute the Fourier series of A and B. The strategy of the computation is based on the ideas of [5] and we first recall some notions presented there. We refer the reader to this paper for more details.

Let h and g have a standard asymptotic behavior in regular domains D_h and D_g and solutions of (4.1):

()

Here, κ_h (resp., κ_g) is an analytic branch of the complex momentum in D_h (resp., D_g), Ψ_h (resp., Ψ_g) is the canonical Bloch solution defined on D_h (resp., D_g), and ζ_h (resp., ζ_g) is the normalization point for h (resp., g).

As the solutions h and g satisfy the consistency condition (4.2), their Wronskian is ε-periodic in ζ.

5.1.1. Arcs

We assume that D_g∩D_h contains a simply connected domain . Let γ be a regular curve going from ζ_g to ζ_h in the following way: staying in D_g, it goes from ζ_g to some point in , and then, staying in D_h, it goes to ζ_h. We say that γ is an arc associated to the triple h, g, and .

As is simply connected, all the arcs associated to the triple, h, g, and . As is simply connected, all the arcs associated to one and the same triple can naturally be considered as equivalent; we denote them by .

We continue κ_h and κ_g analytically along

. From the properties of κ, we deduce that, for V a small neighborhood of γ, one has

()

is called the signature of

, and

the index of

5.1.2. The Meeting Domain

Let be as above. We call a meeting domain, if, in , the functions Im κ_h and Im κ_g do not vanish and are of opposite signs.

Note that, for small values of ε, whether ζ ↦ g(x, ζ) and ζ ↦ h(x, ζ) increase or decrease is determined by the exponential factor and . So, roughly, in a meeting domain, along the lines Im ζ = Const, the solutions h and g increase in opposite directions.

5.1.3. The Action and the Amplitude of an Arc

We call the integral

()

the action of the arc

. Clearly, the action takes the same value for equivalent arcs.

Assume that ℰ(ζ) ∉ P ∪ Q along

. Consider the function

and the 1-form Ω_g(ℰ(ζ)) in the definition of Ψ_g. Continue them analytically along γ. We set

()

A is called the the amplitude of the arc γ. The properties of Ω imply that the amplitudes of two equivalent arcs

coincide.

5.2. Results on the Fourier Coefficients

We recall the following result from [5].

Proposition 5.1. Let d = d(h, g) be a meeting domain for h and g, and let m = m(h, g, d) be the corresponding index. Then

()

where w_m is the constant given by

()

Here ψ₊ = ψ_h and ψ₋ is complementary to ψ₊. The asymptotic (5.8) is uniform in ζ and E when ζ stays in a fixed compact of S(d) and E in a small enough neighborhood of E₀.

5.2.1. The Index m

Let ζ₀ be a regular point. Consider a regular curve γ going from ζ₀ to ζ₀ + 2π. Let κ be a branch of the complex momentum that is continuous on γ. We call the couple (γ, κ) a period. Let (γ₁, κ₁) and (γ₂, κ₂) be two periods. Assume that one can continuously deform γ₁ into γ₂ without intersecting any branching point. By this we define an analytic continuation of κ₁ to γ₂. If the analytic continuation coincides with κ₂, we say that the periods are equivalent.

Consider the branch κ along the curve γ of a period (γ, κ). In a neighborhood of ζ₀, the starting point γ, one has

()

The numbers σ = σ(γ, κ) and m = m(γ, κ) are called, respectively, the signature and the index of the period (γ, κ). They coincide for equivalent periods.

Recall that

()

is the preimage with respect to ℰ of the union of the spectral gaps of H₀. One has the following.

Lemma 5.2 (see [10].)Let (γ, κ) be a period such that γ starts at a point ζ₀ ∉ 𝒢.Assume that γ intersects 𝒢 exactly n times (n ∈ ℕ) and that at all intersection points, W^′ ≠ 0. Let r₁, …, r_n be the values that Reκ takes consecutively at these intersection points as ζ moves along γ from ζ₀ to ζ₀ + 2π. Then,

()

5.3. The Fourier Coefficients

5.3.1. For B

By (5.3), we have to compute w(f(·, ζ), f(·, ζ + 2π)). With this aim in view, we apply the construction done in Section 5.1 with

()

We will start by the following.

5.3.2. Above the Real Line

We take the meeting domain D₀ as the subdomain of the strip 0 < Im ζ < Y between the Stokes lines and In this domain we have Im κ_g = −Im κ_h < 0. Indeed we notice that the sign of Im κ changes to opposite one as ζ intersects 𝒵 at a point where W^′ ≠ 0 taking into account that κ_g(ζ) = κ_h(ζ + 2π), and to go from ζ to ζ + 2π one has to intersect ℬ₁.

The arc γ₀ connects the point ζ_g to ζ_h. By (5.14), this defines the period (γ₀, κ_g). Using (5.15), one gets that m(f(·, ζ), f(·, ζ + 2π, D₀)) = m(γ₀ + 2π, κ) [5].

We use Lemma 5.2 to compute the index. To do this, we have to compute Reκ at the intersection of γ₀ + 2π and 𝒢.

As ζ → Reκ(ζ) is constant on any connected component 𝒢_j of 𝒢. Let us start by defining the index of 𝒢_j, the result of the alternated character of the coefficients (…, +, −, +, −, …) due to the crossing of 𝒢_j (see Lemma 5.2). We notice that .

We set

()

Here n_j is the number of extremum in 𝒢_j, and o_l is the order of the lth extremum. The following relations hold:

()

and for 2 ≤ j ≤ N,

()

Without loss of generality we assume that Reκ = 0 on

. By the above notation, we get that

()

Here p_i is the index of ℬ_i and n = N_N.

Now using (5.3) for B and Proposition 5.1 we get

()

5.3.3. Below the Real Line

Below the real line, we take the domain of the strip −Y < Im ζ < 0 located between the stokes line and as a regular domain, which we denote by . We set then it defines a period, and so . The curve defining a period equivalent to is represented in Figure 6.

The computation of the index

of 𝒢_j gives in this case that

()

By this notation we get that

()

Using (5.3) for B and Proposition 5.1 we get

()

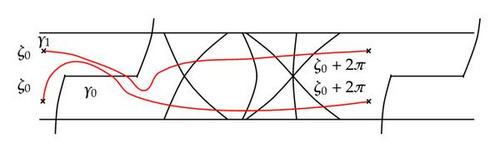
5.4. For A

For the computation of A using (5.3), we have to compute w(f^*(·, ζ), f(·, ζ + 2π)). It suffices to apply the method presented in Section 5.1 with

()

5.4.1. Above the Real Line

In this case, the meeting domain, is the subdomain of the strip {0 < Im ζ < Y} located between the lines and the symmetric to with respect to ℝ. The arc defines a period in Figure 7 we represent the curve

Similarly to the computation of B, we define the index

of 𝒢_j, and in this case, we have

()

By this notation we get that

()

Using (5.3) for A and Proposition 5.1 we get that

()

5.4.2. Below the Real Line

In this case,

the meeting domain, is the subdomain of the band {−Y < Im ζ < 0} located between the lines

, symmetric of

with respect to ℝ, and

. The arc

defines a period

; the curve

is represented in Figure 7. One obtains that

()

and for 2 ≤ j ≤ N,

()

So by the above notation we get that

()

One obtains that

, and

()

5.4.3. The Proof of (3.15)

Let g ∈ 𝒢. Let V(g) be a complex neighborhood of g sufficiently small so that it contains only two branch points of κ, namely, the ends of g. Let γ_g be a curve in V(g)∖g; the tunneling action is defined as From [5], we recall the following lemma.

Lemma 5.3 (see [5].)Let E ∈ J. If γ_g is positively oriented, then

()

Here, in the left-hand side, one integrates in the increasing direction on the real axis.

Below we give details only for A₊; the same way could be used to obtain the result for A₋ and B − ±.

We recall that the definition of the amplitude of an arc γ is given in (5.7) and the coefficient A₊ is defined in (5.31). This definition implies that

is independent of ε, continuous in E, and does not vanish; so we get that for V₀ a small constant neighborhood of E₀ ∈ J, ∃ C₁, C₂ > 0 such that

()

Let

be the arc going near the real line and going around the branch points between ζ₀ and ζ₀ + 2π (the beginning and the end of γ) along infinitesimally small circles. One has

()

Im κ_g < 0, inside each of the intervals of integration. Using (5.36), the expression −2∫_gIm κdζ is equal to S(g), the tunneling action, because S(g) is taken positive. Then we get

()

This ends the proof of (3.15) for A₊.

Acknowledgments

The authors would like to thank F. Klopp for proposing this problem and many valuable comments and remarks and the referee for his valuable comments which improve the paper. M. Marx thanks M. Ben Ammar the director of the Research Unity 01/UR/15-01 for the financial support by paying her mission in Tunisia. H. Najar thanks R. Assel and M. Dimassi for suggesting some interesting references and for their stimulating discussion. Researches are supported by CMCU 09G1504 and the research Unity 01/UR/15-01 projects.

References

1 Pastur L. and Figotin A., Spectra of Random and Almost-Periodic Operators, 1992, 297, Springer, Berlin, Germany, Grundlehren der Mathematischen Wissenschaften, MR1223779.
10.1007/978-3-642-74346-7
Google Scholar
2 Avron J. and Simon B., Almost periodic Schrödinger operators. II. The integrated density of states, Duke Mathematical Journal. (1983) 50, no. 1, 369–391, MR700145, https://doi.org/10.1215/S0012-7094-83-05016-0, ZBL0544.35030.
10.1215/S0012-7094-83-05016-0
Web of Science® Google Scholar
3 Ziman J. M., Principles of the Theory of Solids, 1972, 2nd edition, Cambridge University Press, London, UK, MR0345569.
10.1017/CBO9781139644075
Google Scholar
4 Buslaev V. S. and Fedotov A. A., Bloch solutions for difference equations, Algebra i Analiz. (1995) 7, no. 4, 74–122, MR1356532, ZBL0859.39001.
Google Scholar
5 Fedotov A. and Klopp F., On the singular spectrum for adiabatic quashuiti-periodic Schrödinger operators in the real line, Annales Henri Poincaré. (2005) 5, 1–5.
Web of Science® Google Scholar
6 Eastham R., The Spectral Theory of Periodic Differential Operators, 1973, Scottish Academic Press, Edinburgh, UK.
Google Scholar
7 Reed M. and Simon B., Methods of Modern Mathemathical Vol. IV: Analysis of Operators, 1978, Academic Press, New York, NY, USA.
Google Scholar
8 Fedotov A. and Klopp F., Anderson transitions for a family of almost periodic Schrödinger equations in the adiabatic case, Communications in Mathematical Physics. (2002) 227, no. 1, 1–92, MR1903839, https://doi.org/10.1007/s002200200612, ZBL1004.81008.
10.1007/s002200200612
Web of Science® Google Scholar
9 Cycon H. L., Froese R. G., Kirsch W., and Simon B., Schrödinger Operators with Application to Quantum Mechanics and Global Geometry, 1987, Springer, Berlin, Germany, Texts and Monographs in Physics, MR883643.
Web of Science® Google Scholar
10 Fedotov A. and Klopp F., On the absolutely continuous spectrum of one-dimensional quasi-periodic Schrödinger operators in the adiabatic limit, Transactions of the American Mathematical Society. (2005) 357, no. 11, 4481–4516, https://doi.org/10.1090/S0002-9947-05-03961-9, MR2156718, ZBL1101.34069.
10.1090/S0002-9947-05-03961-9
Web of Science® Google Scholar
11 McKean H. P. and van Moerbeke P., The spectrum of Hill′s equation, Inventiones Mathematicae. (1975) 30, no. 3, 217–274, MR0397076, https://doi.org/10.1007/BF01425567, ZBL0319.34024.
10.1007/BF01425567
Web of Science® Google Scholar
12 Titschmarch E. C., Eigenfunction Expansions Associated with Second-Order Differential Equations Part II, 1958, Clarendon Press, Oxford, UK, New York, NY, USA, 1978.
Google Scholar
13 Fedotov A. and Klopp F., A complex WKB method for adiabatic problems, Asymptotic Analysis. (2001) 27, no. 3-4, 219–264, MR1858917, ZBL1001.34082.
Web of Science® Google Scholar
14 Marx M., On the eigenvalues for slowly varying perturbations of a periodic Schrödinger operator, Asymptotic Analysis. (2006) 48, no. 4, 295–357, MR2256576, ZBL1124.34063.
Web of Science® Google Scholar
15 Fedoryuk M. V., Asymptotic Analysis, 1993, Springer, Berlin, Germany, MR1295032.
10.1007/978-3-642-58016-1
Google Scholar
16 Fedotov A. and Klopp F., Geometric tools of the adiabatic complex WKB method, Asymptotic Analysis. (2004) 39, no. 3-4, 309–357, MR2097997, ZBL1070.34124.
Web of Science® Google Scholar
17 Klopp F. and Marx M., Resonances for slowly varying perturbations of one-dimensional periodic Schrödinger operators, Séminaire sur les Equations aux Dérivées Partielles de l′ Ecole Polytechnique (2005-2006), 2006, 4, Ecole Polytechnique, Palaiseau, France, 18, MR2276070, ZBL1118.34082.
Google Scholar
18 Marx M., Etude de perturbations adiabatiques de l′équation de Schrödinger périodique, Ph.D. thesis, 2004, Université Paris XIII, Paris, France.
Google Scholar

Citing Literature

All articles

On the Singular Spectrum for Adiabatic Quasiperiodic Schrödinger Operators

Abstract

1. Introduction

1.1. Results and Discussions

1.1.1. Assumptions on the Potentials

1.1.2. Assumptions on the Energy Region

1.1.3. The Periodic Operator

1.1.4. The Geometric Assumption

1.1.5. The Main Result

2. Periodic Schrödinger Operators

2.1. Geometric Description

2.1.1. The Set W−1(ℝ)

2.1.2. Notations and Description of (E − W) −1(σ(H0))

2.2. Bloch Solutions

2.3. The Bloch Quasimomentum

2.4. A Meromorphic Function

2.4.1. The Complex Momentum

2.4.2. Index of an Interval

2.4.3. Tunneling Coefficients

3. The Proof of Theorem 1.2

3.1. The Asymptotics of the Lyapunov Exponent

3.1.1. Spectral Results

3.2. The Monodromy Matrix and the Lyapunov Exponents

3.2.1. Definition of the Monodromy Matrix

3.3. The Lyapunov Exponents and the Monodromy Equation

3.4. The Asymptotics of the Monodromy Matrix

3.5. The Proof of Theorem 3.1

3.5.1. The Upper Bound

3.5.2. The Lower Bound

3.5.3. Conclusion

4. The Complex WKB Method for Adiabatic Problems

4.1. Standard Behavior of Consistent Solutions

4.1.1. Canonical Bloch Solutions

4.2. Solutions Having Standard Asymptotic Behavior

4.3. Some Results on the Continuation of Asymptotics

4.3.1. Description of the Stokes Lines near

4.3.2. Definition

4.3.3. Stokes Lines for E0 ∈ J

4.4. Construction of a Consistent Basis near

5. The Proof of Theorem 3.4

5.1. Strategy of the Computation

5.1.1. Arcs

5.1.2. The Meeting Domain

5.1.3. The Action and the Amplitude of an Arc

5.2. Results on the Fourier Coefficients

5.2.1. The Index m

5.3. The Fourier Coefficients

5.3.1. For B

5.3.2. Above the Real Line

5.3.3. Below the Real Line

5.4. For A

5.4.1. Above the Real Line

5.4.2. Below the Real Line

5.4.3. The Proof of (3.15)

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

2.1.1. The Set W⁻¹(ℝ)

2.1.2. Notations and Description of (E − W) ⁻¹(σ(H₀))

4.3.3. Stokes Lines for E₀ ∈ J