Underlay cognitive radios (UCRs) allow a secondary user to enter a primary user′s spectrum through intelligent utilization of multiuser channel quality information (CQI) and sharing of codebook. The aim of this work is to study two-user Gaussian UCR systems by assuming the full or partial knowledge of multiuser CQI. Key contribution of this work is motivated by the fact that the full knowledge of multiuser CQI is not always available. We first establish a location-aided UCR model where the secondary user is assumed to have partial CQI about the secondary-transmitter to primary-receiver link as well as full CQI about the other links. Then, new UCR approaches are proposed and carefully analyzed in terms of the secondary user′s achievable rate, denoted by C₂, the capacity penalty to primary user, denoted by ΔC₁, and capacity outage probability. Numerical examples are provided to visually compare the performance of UCRs with full knowledge of multiuser CQI and the proposed approaches with partial knowledge of multiuser CQI.

1. Introduction

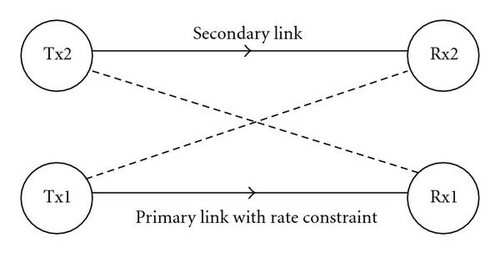
Cognitive radios convey a dynamic and flexible spectrum allocation policy that allows a secondary user to access a primary user′s spectrum through exploitation of advanced air-interface techniques and intelligent utilization of multiuser side information such as user activity, channel quality information (CQI), message, codebook, and location information, and so forth. A good tutorial about cognitive radios can be found in [1], focused on the signal-processing perspective, and in [2], focused on the information-theoretic perspective. One group of cognitive radios is known as the interweave paradigm, where a secondary user can opportunistically enter temporary spectrum holes and white spaces existing in both licensed or unlicensed radio spectrum [3]. Fast and reliable spectrum sensing techniques are the key to the success of interweave cognitive radios. The other group of cognitive radios includes overlay and underlay paradigms, where the secondary user and the primary user form a cognitive interference channel (e.g., [4–6]). Specifically, the overlay cognitive user is able to sense the primary user′s message, and then employs advanced coding schemes such as the Gel′fand-Pinsker code [7] or the dirty-paper code [8] for interference precancellation. In the underlay paradigm, the secondary user enters the primary spectrum only when its activity will not cause considerable interference or capacity penalty to the primary user. Measure of interference requires knowledge about multiuser CQI. The focus of this paper is on the two-user Gaussian underlay cognitive radios (UCR).

Figure 1 illustrates an example of two-user UCR system accommodating one primary transmitter (Tx1) and receiver (Rx1) pair in System number 1 and one secondary transmitter (Tx2) and receiver (Rx2) pair in System number 2. The block diagram of this UCR system is depicted in Figure 2(a). In the flat-Gaussian scenario, this UCR system can be described as the following linear model(this is a well-recognized model in the literature [8–12] where both users are assumed to employ simple random codes. Although rate-splitting codes have been recently introduced to cognitive radio channels, the focus of this paper will be on this simple system model)

(1)

(2)

where X_i stands for the signal sent by the transmitter Txi with power P_i and rate R_i, Y_j for the signal received at the receiver Rxj, a_ij for the channel coefficient of the Txi-Rxj link, V for the Gaussian noise with zero mean and variance N_o. This linear model shows that the UCR system is a special case of interference channels presented in [9, 10], but the interference term (a₂₁X₂) in (1) must not cause considerable capacity penalty to the primary user. According to the multiuser decoding capability, we can divide the UCR system into the following four groups. Detailed introduction about these four modes can be found in Sections 3–6, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of an example about the two-user UCR system and a location-aided approach.

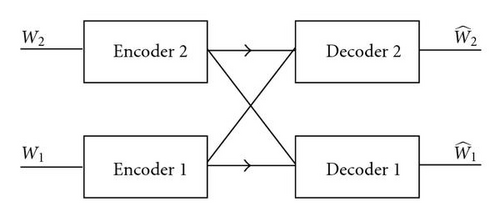
(1) Individual Decoding Both the primary user and the secondary user always deal with the mutual interference as noise in their decoding process.

(2) Secondary-User Side Multiuser Decoding (SSMD) The secondary user optimally deals with the interference term (a₁₂X₁) in its decoding process. But, the primary user always deals with the interference term (a₂₁X₂) as noise.

(3) Primary-User Side Multiuser Decoding (PSMD) The primary user optimally deals with the interference term (a₂₁X₂) in its decoding process. But, the secondary user always deals with the interference term (a₁₂X₁) as noise.

(4) Two Sides Multiuser Decoding (TSMD) Both the primary user and the secondary user perform an optimal treatment about the corresponding interference term in their decoding process.

Key physical layer issues this work seeks to address are mainly in two folds:

Issue 1 Provided full knowledge about multiuser CQI, what is the fundamental relationship between the secondary user′s achievable rate, denoted by C₂, and capacity penalty to the primary user, denoted by ΔC₁? What are criteria for Tx2 to perform efficient power allocation? Those questions require an answer for various UCR modes.

Issue 2 In many practical environments, having full knowledge of CQI about all links of the UCR system is not a suitable assumption. What are more suitable assumptions in practice? What is the efficient UCR strategy under new assumptions? What is the secondary user′s achievable rate? Those questions require a satisfactory answer.

The primary objective of this work is to partially answer the above questions through a study from the information-theoretic viewpoint. In order to focus on the major technical issues, the following assumptions are made throughout this paper.

(A1) We consider a two-user UCR system accommodating one primary transmitter-receiver pair and one secondary transmitter-receiver pair. This assumption can be easily assured by introducing orthogonal multiple-access schemes such as TDMA or FDMA to multiuser systems.
(A2) Users in the system are synchronized in both the time and frequency. Although the time-frequency synchronization is a challenge in practice, we would argue that the achievable rate produced under this assumption can be regarded as an upper bound of the practical performance.
(A3) Both receivers employ maximum-likelihood (ML) detector/decoder to offer the optimum decoding performance.

Contribution towards this work includes the following

(1) The first work is to answer those questions listed in Issue 1. Provided full knowledge of multiuser CQI, the fundamental relationship between C₂ and ΔC₁ is investigated for four UCR groups. Criteria for efficient power allocation at Tx2 are established. The produced results are the key to new UCR strategies proposed for the case with partial knowledge of the multiuser CQI.

(2) As a starting point of the work towards Issue 2, we study modeling of UCR systems in the absence of full knowledge of multiuser CQI. After a careful justification, we establish an UCR system model, where the secondary user is assumed to have partial knowledge of CQI about the Tx2-Rx1 link, and have full knowledge of CQI about the other links. Location-aided UCR is employed as an example to support our justification.

(3) We propose new spectrum-access approaches for various UCR groups by assuming the availability of p.d.f. of CQI about the Tx2-Rx1 link. Power allocation criteria are carefully investigated in terms of C₂, ΔC₁, and capacity outage probability. (In practice, the performance of power allocation will be influenced by air-interfaces and synchronization errors. The results presented in this paper are to provide an information-theoretic guidance to practical designs.) Assuming the channel to be Rayleigh, numerical results are provided to visually show the performance of UCRs with full knowledge of multiuser CQI and the proposed approaches with partial knowledge of multiuser CQI.

The rest of this paper is organized as follows. Section 2 offers a brief review about capacity theorem of Gaussian interference channel (GIC) and relates it to the UCR system. Moreover, modeling about the UCR system with partial knowledge of multiuser CQI is also presented. Technical contributions towards four UCR groups are presented in Sections 3–6, respectively. Section 7 draws the conclusion.

2. System Model and Preparation

This section first presents capacity theorem about two-user GIC and its relationship with the UCR system, and then presents modeling of the UCR system with partial knowledge of the multiuser CQI.

2.1. Two-User UCR with Full Multiuser CQI

The UCR system is a special case of interference channels. The information-theoretic research towards interference channels started from Carleial′s work published in [9]. Although lots of research efforts have been paid in the last 30 years, capacity region of interference channels has been found only for the case of strong interference [13]. To the best of our knowledge, the state-of-the-art capacity bound of two-user GIC has recently been reported in [11, 12]. Next, we provide a brief review about capacity theorem of two-user GIC, which offers the theoretical support to our further investigation about the two-user UCR system.

2.1.1. Two-User GIC with Strong Interference

In the linear model (1)–(2), the case of strong interference denotes the scenario |a₁₂ | ≥|a₁₁| and |a₂₁ | ≥|a₂₂| [10]. In this case, the two-user GIC is in fact a compound Gaussian multiple-access channel (MAC), whose capacity region is known as the following union [14]:

(3)

where

denotes the instantaneous signal-to-noise ratio (SNR) and 𝒞[x]≜log ₂(1 + x). Provided (3) and the assumption that users share their codebook, each receiver can reliably recover the message sent by Tx1 and Tx2, respectively.

2.1.2. Two-User GIC with Weak or Mixed Interference

This scenario includes cases other than the case of strong interference. The closed form of capacity region is unknown to this date. A lookup table (but incomplete) about the channel capacity with respect to various channel conditions has been reported in [12]. Alternatively, we can divide the two-user GIC into the following three groups with respect to the way of dealing with the interference. The following result is adequate for us to investigate the two-user Gaussian UCR system.

Group I Each receiver can reliably decode the message sent by Tx1 and Tx2, respectively. The achievable rate region, denoted by ℛ^I, is (3).

Group II Each receiver can only decode the message sent by its corresponding transmitter. The interference will be regarded as noise. The achievablerate region, denoted by ℛ^II, is (see [9])

(4)

Group III One receiver can decode the message sent by both transmitters, and the other can only decode the message sent by its corresponding transmitter. In this group, the achievable rate region, denoted by ℛ^III, is (see [12])

(5)

Provided γ_ij, _i,j=1,2, we can obtain the maximum sum-rate, max (R₁ + R₂), through a comparison between ℛ^I, ℛ^II, and ℛ^III.

2.1.3. Two-User Gaussian UCR

The UCR system is modeled as an interference channel where the primary user wants to keep its interference-free capacity. But in many cases, the secondary user will cause capacity penalty ΔC₁ to the primary user. Hence, the primary user′s capacity is expressible as [5]

(6)

and the secondary user′s achievable rate is (see [12])

(7)

Define

(8)

where ρ is a positive coefficient. Equation (6) is expressible as

(9)

In order to keep the capacity penalty to be reasonably small, we usually let ρ ≪ 1.

2.2. Two-User UCR with Partial Multiuser CQI

In practice, the primary transmitter-receiver pair may operate in the frequency-division duplex (FDD) manner, where the transmitter Tx1 periodically sends training sequences to support channel estimation and coherent detection/decode at the receiver Rx1. Rx1 informs Tx1 regarding the CQI of Tx1-Rx1 link through a feedback channel. On the secondary-user side, we assume that Rx2 can communicate with Tx2 through a feedback channel. This feedback channel is orthogonal to the primary user′s frequency band and mainly for the purpose of signaling. Based on the above system description, we provide the following justification of assumptions about the knowledge of CQI:

(i) The secondary receiver Rx2 listens to the conversation between Tx1 and Rx1. Then, Rx2 can estimate the CQI of Tx1-Rx2 link.

(ii We assume that Rx1 employs a simple common codebook such as repetition code to perform the feedback of CQI. Then, Rx2 can obtain the CQI about Tx1-Rx1 link through sensing of the primary user′s feedback channel.

(iii) At the beginning of cognitive communication, Rx2 requests Tx2 to send a training sequence over the primary spectrum. This offers the knowledge of CQI about the Tx2-Rx2 link, but introduces a short burst of interference to the primary user. We argue that this burst of interference will not cause considerable performance loss to the primary user.
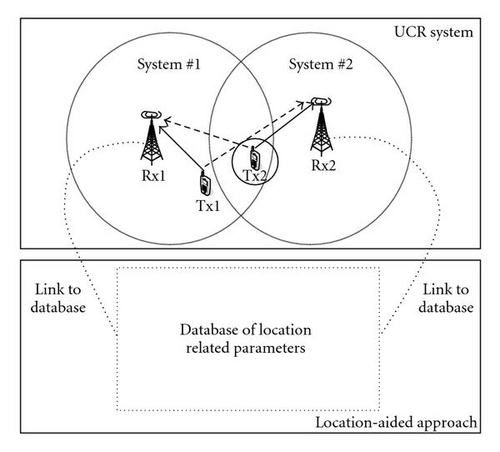
(iv) Rx1 may estimate the CQI of Tx2-Rx1 link if appropriate, but does not show this information in its feedback channel due to an upper-layer protocol. In this case, Rx2 cannot know the CQI of Tx2-Rx1 link. Then, our assumption is that the secondary user knows the p.d.f. of CQI about the Tx2-Rx1 link. This assumption is suitable for a scenario such as where the secondary user has the location information about itself and the primary user. The secondary user can access a well-designed and maintained database, which records the p.d.f. of CQI between two locations. Figure 1 illustrates an example of location-aided UCR system, where Rx1 and Rx2 are fixed network nodes such as base-stations or access points, and Tx1 and Tx2 are mobile stations. The database has a lookup table about the p.d.f. of CQI between each fixed network node and a certain area such as the black circle with solid line. Provided the location of Tx2, Rx2 knows which circle Tx2 is currently in, and thus can look up the database to find out the p.d.f. of CQI about the Tx2-Rx1 link. Recently, how to design and maintain the location-related database is becoming an important research topic. However, it is out of the scope of this paper. Further information about location estimation and location-related database can be found in European ICT WHERE [15].

As a summary, when we investigate the UCR strategy with partial multiuser CQI, the following assumptions are made in addition to (A1)–(A3):

(A4) Rx2 has full knowledge of CQI about the Tx1-Rx1 link, the Tx1-Rx2 link, and the Tx2-Rx2 link, but only knows p.d.f. of CQI about the Tx2-Rx1 link, denoted by p(|a₂₁|²) as well as the mean E(|a₂₁|²).

(A5) Rx2 determines the secondary user′s power and transmission rate, and then informs Tx2 through the feedback channel.

3. The Individual Decoding Mode

Figure 2(b) depicts the individual decoding mode where each receiver only wants to decode the message sent by its corresponding transmitter, and deals with the corresponding interference as noise. This mode is suitable for the following cognitive radio scenarios:

(i)
Both the primary user and secondary user employ their private codebook;
(ii)
Even if both users employ a common codebook, each receiver cannot decode the other user′s message due to reasons such as channel conditions and upper layer protocols.

In this situation, the UCR system can be regarded as a simple collection of individual links. This mode has recently received an intensive investigation in both the basic and system-level research, for example, in [16, 17].

3.1. Capacity Results with Full Knowledge of CQI

This simple mode is already mature in terms of capacity results. The channel capacity for both users is given by (4). The capacity penalty ΔC₁ is calculated as

(10)

Equations (4) and (10) show a known result that increasing the secondary user′s power P₂ will increase both C₂ and ΔC₁. Applying (8) into (10), we can relate P₂ to the capacity-penalty coefficient ρ as

(11)

Given a coefficient ρ, the secondary user′s power should be no larger than (11). Otherwise, the primary user would suffer capacity outage.

Remark 1. A remarkable issue is that ΔC₁ in (10) is a monotonically decreasing function of γ₁₁ due to the partial derivative (∂ΔC₁)/(∂γ₁₁) < 0. This means that the primary user operating at a high-SNR scenario is less sensitive to the interference. Considering a high-SNR scenario that fulfills the conditions (C1) γ₁₁ ≫ 1, and (C2) γ₁₁ ≫ γ₂₁, (10) approximates to

(12)

Plugging (8) into (12) leads to

(13)

This simplified result can be utilized to allocate the secondary user′s power when the primary user operates in the high-SNR range.

3.2. The UCR Strategy with Partial Multiuser CQI

Section 3.1 shows that, provided the power P₂, the secondary user can employ (4) to configure its transmission rate. However, using (11) or (13) to configure P₂ requires the knowledge about , which is supposed to be unknown in some situations. Next, we propose a new power-allocation criterion based on the assumption (A4).

Criterion. The power P₂ should be appropriately configured so that the capacity-outage probability of primary user is not larger than a given threshold 𝒪_t.

Based on Criterion 1, the power-allocation strategy can be summarized into the following two steps.

Step 1. Outage probability to the primary user is a function of the SNR mean of Tx2-Rx1 link denoted by . Motivated by this fact, the secondary user can first calculate the outage probability for a given p(|a₂₁|²), and then determine a threshold corresponding to 𝒪_t.

Step 2. The secondary user can access the primary spectrum for the condition . The maximum of P₂ is therefore given by

(14)

The secondary user′s transmission rate can be calculated by applying (14) into (4). Next, we will use a numerical example to introduce about how to determine the threshold

, and to show the performance in this example.

3.3. Numerical Example

Define an instantaneous SNR threshold γ_t as

(15)

Equation (11) indicates that the secondary user will cause capacity outage to the primary user when γ₂₁ > γ_t. Assume the p.d.f. p(|a₂₁|) to be Rayleigh as an example. The probability for the event (γ₂₁ > γ_t) to happen can be calculated as [18]

(16)

where Pr(·) denotes the probability. According to Criterion 1, the threshold

should be carefully chosen to fulfill the following condition:

(17)

We apply the definition of γ_t (15) in (17) and obtain

(18)

Moreover, when the primary user fulfills the high-SNR condition (C1)-(C2), we can use (13) to define

(19)

Applying (19) into (17) results in

(20)

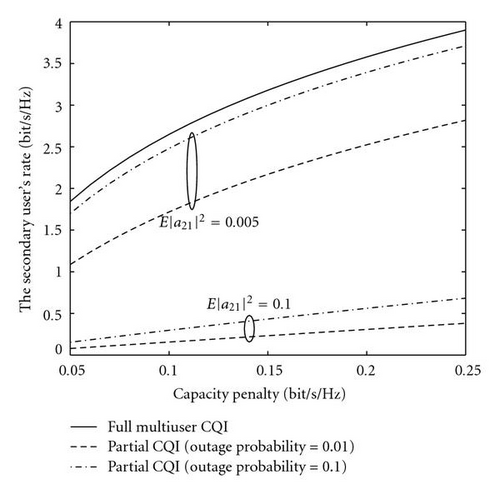
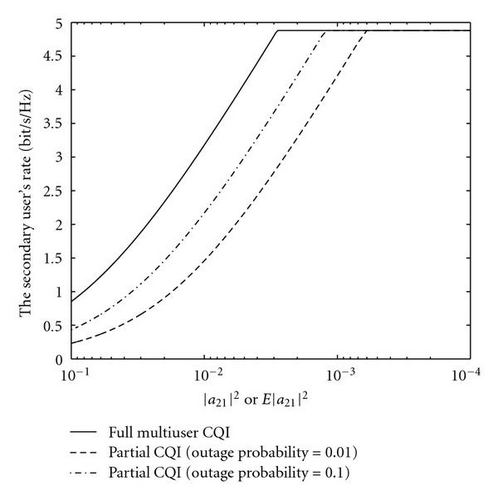
Based on the above analytical results, we use a visual example to exhibit the performance. In this example, the UCR system is configured as |a₁₁ | = 1, |a₂₂ | = 1, |a₁₂ | = 0.1. The primary user′s power-to-noise ratio is P₁/N_o = 16 dB. The secondary user′s power-to-noise ratio is also limited by 16 dB. This ratio is one of typical configurations for high-data-rate systems. For the scenario with full multiuser CQI, we set |a₂₁ | = 0.1. Figure 3 illustrates the secondary user′s achievable rate (see (4)) against the capacity penalty ΔC₁ (see (10)) for cases with full or partial multiuser CQI. It is observed that the secondary user′s achievable rate generally increases with the pay of capacity penalty to the primary user. Moreover, in the scenario with partial multiuser CQI, the secondary user shows increased achievable rate for the case of larger outage probability, for example, 𝒪_t = 0.1 or smaller E(|a₂₁|²), for example, E(|a₂₁|² = 0.005). Figure 4 illustrates the secondary user′s achievable rate with respect to the channel quality of Tx2-Rx1 link (ΔC₁ = 0.15 bit/sec/Hz). It shows that the UCR approach with partial CQI offers the same performance as the UCR with full CQI when the Tx2-Rx1 channel is deep faded.

4. The SSMD Mode

Figure 2(c) depicts the SSMD mode where each receiver wants to decode the message sent by its corresponding transmitter. The secondary receiver Rx2 will decode the primary user′s message if appropriate. The primary receiver Rx1 always deals with the interference term (a₂₁X₂) as noise. This mode is suitable for the following cognitive radio scenario:

(i)
The secondary user knows the primary user′s codebook, and thus has a chance to decode the primary user′s message. This is possible if the primary user is either using a common codebook or broadcasting its own codebook to support, for example, user cooperation. On the other hand, the primary user may be not aware of the existence of secondary user, or does not know the secondary user′s private codebook.

In this situation, the receiver Rx2 can reliably decode the primary user′s message only for the channel condition |a₁₂ | ≥|a₁₁|, otherwise the SSMD mode reduces to the individual decoding mode presented in Section 3. (Multiuser information theory about the interference channel shows that Rx2 can decode the signal X₁ if the rate of X₁ is not larger than the achievable rate of Tx1-Rx2 link. However, the UCR channel requires the rate of X₁ to be constrained only by the achievable rate of Tx1-Rx1 link. In the case of weak interference, the Tx1-Rx1 link offers larger achievable rate than the Tx1-Rx2 link. Rx2 cannot decode X₁ if the rate of X₁ is larger than the achievable rate of Tx1-Rx2 link.) Therefore, the focus of SSMD mode is on the case |a₁₂ | ≥|a₁₁|.

4.1. Capacity Results with Full Multiuser CQI

Suppose the channel condition |a₁₂ | ≥|a₁₁|. The transmission rate for both users is given in (5) by setting i = 2 and j = 1. More precisely, the capacity penalty ΔC₁ is (10), and the secondary user′s achievable rate is expressible as

(21)

This result is subject to the power constraint of P₂ given in (11).

Remark 2. For the high-SNR conditions (C1), (C2) and the case |a₁₂ | ≥|a₁₁|, we can apply (10) and (12) into (21) to obtain

(22)

and the transmit power P₂ is limited by (13). Next, we will use the above capacity results to investigate the UCR strategy with partial multiuser CQI.

4.2. The UCR Strategy with Partial Multiuser CQI

Major difference between the SSMD mode and the individual decoding mode is that the secondary user has improved achievable rate due to the availability of primary user′s codebook. However, on the primary user′s side, there is no difference between these two modes. The spectrum access and power allocation strategy for the SSMD mode should also obey Criterion 1 so as to fulfill the requirement of outage probability. Therefore, the UCR strategy for SSMD mode is the same as that for the individual mode, and the transmit-power P₂ is limited by (14). The secondary user′s transmission rate is restricted by the result produced by applying (14) in (21).

Apart from (21), numerical results for the SSMD mode is the same as those for the individual decoding mode. Moreover, (21) is also a well-known result in the domain of multiuser information theory. Therefore, we do not provide a numerical example for this mode.

5. The PSMD Mode

This mode is referred to as a scenario where the secondary user does not know the primary user′s codebook, but share its own codebook through upper-layer protocols. In this case, the primary user has a chance to decode the secondary user′s message, and thus has the potential to cancel the interference caused by the secondary user. On the other hand, the secondary user has to deal with the interference term (a₁₂X₁) as noise.

5.1. Capacity Results with Full Multiuser CQI

In order to ensure reliable communication of the Tx2-Rx2 pair, the secondary user′s transmission rate is restricted by the second formula in (4). On the other hand, Section 2.1 Group III shows that the primary user can reliably decode the secondary user′s message only when

(23)

where C₁ is given by (9). Moreover, the primary user′s capacity should fulfill the following condition:

(24)

where the interference term (a₂₁X₂) in (1) is treated as noise.

Theorem 1. Suppose |a₂₁ | ≠ 0 and ρ = 0, the secondary user′s achievable rate is

(25)

for the channel condition

(26)

otherwise

(27)

Proof. For the case of ρ = 0, the results (4) and (23) show that the secondary user′s transmission rate should fulfill

(28)

otherwise, either the primary user or the secondary user cannot perform reliable communication. Then, it is straightforward to justify that the right-hand term in (25) is smaller than the right-hand term in (27) only for the channel condition (26) to be satisfied. This theorem is therefore proved.

Theorem 1 gives the secondary user′s achievable rate subject to zero capacity-penalty to the primary user. It can be observed that R₂ would be almost zero if the channel gain |a₂₁| is deep fade. This result is inconsistent with the original idea of UCR which takes advantage of the case |a₂₁ | ≈ 0. In other words, it is not wise to always target on zero capacity-penalty to the primary user. Below provides two criteria to handle the issue of capacity penalty.

Criterion. The pay of capacity penalty offers improvement of the sum rate of UCR, that is, max (R₁ + R₂).

Criterion. The capacity penalty is tolerable to the primary user, for example, ρ ≪ 1.

Theorem 2. Suppose the following channel condition:

(29)

the secondary user′s achievable rate is (25) subject to the power constraint (11).

Proof. The result (23) indicates that the pay of capacity penalty will not improve max (R₁ + R₂) if the primary user wants to reliably decode the secondary user′s message. Hence, the only case to have an improved max (R₁ + R₂) is to deal with the interference term (a₂₁X₂) as noise, for which R₂ is only limited by (25). Moreover, the following inequality has to be satisfied so as to fulfill Criterion 2:

(30)

Solving (30) leads to the channel condition (29). In order to fulfill Criterion 3, the transmit power P₂ should be limited by (11). This theorem is therefore proved.

According to Theorems 1 and 2, we can conclude the following results:

(1) For the channel condition (26), Tx2 can talk to Rx2 at a rate (25) without causing capacity penalty to the primary user. The transmit power P₂ is limited by the secondary user′s local power constraint.

(2) For the channel condition (29), Tx2 can talk to Rx2 at a rate (25). The transmit power P₂ is limited by (11) to keep the capacity penalty ΔC₁ under an acceptable level.
(3) For channel conditions other than (26) and (29), Tx2 can talk to Rx2 at a rate (27) without causing capacity penalty to the primary user. The transmit power P₂ is limited by the secondary user′s local power constraint.

5.2. The UCR Strategy with Partial Multiuser CQI

Section 5.1 shows that the spectrum access and power-allocation strategy for the PSMD mode requires the full knowledge of |a₂₁|. Here, we present a new UCR strategy under the assumption (A4). The main idea is summarized as follows.

Define a threshold of probability denoted by ϵ. Based on Theorems 1 and 2, the secondary user will access the primary spectrum for the following three cases.

Case 1. Suppose

(31)

the secondary user will enter the primary spectrum at a rate (25) with P₂ limited by its local power constraint. In this case, the primary user does not have a capacity penalty, but suffers capacity outage with the probability (1 − ϵ).

Case 2. Suppose

(32)

the secondary user′s transmission rate is also (25). In this case, the primary user deals with the interference as noise, and thus has the capacity penalty (10). Moreover, the secondary user′s power P₂ should be carefully configured in terms of capacity penalty and outage probability to the primary user. This issue will receive further investigation by employing a numerical example.

Case 3. Suppose

(33)

Theorem 1 shows that the secondary user can talk at a rate (27). Unfortunately, the secondary user does not know |a₂₁|, and thus cannot straightforwardly employ (27) to determine its achievable rate. In this case, we propose to use the following formula produced by replacing the term γ₂₁ with (P₂ℒ)/(N_o) in (27)

(34)

where ℒ ∈ (|a₂₂|²λ₂, |a₂₂|²λ₁) is a scaling factor. This case will be further investigated through a numerical example.

Finally, for cases other than (31)–(33), the secondary user will not enter the primary spectrum.

5.3. Numerical Example

Equations (31)–(33) show that the proposed UCR strategy is based on the statistical relationship between |a₂₁| and |a₂₂|. Considering |a₂₁| to be Rayleigh as a numerical example, we investigate the performance of the proposed approach.

Case 1. The key issue of this case is to find out the relationship between E(|a₂₁|²) and the threshold of outage probability 𝒪_t, and then to link this relationship to the spectrum-access strategy. The following result is derived for this issue.

Corollary 1. Given a threshold of the primary user′s outage probability 𝒪_t, the condition for (31) to be satisfied is

(35)

Proof. We first rewrite (31) into

(36)

Using the result derived in [18], (36) becomes

(37)

Given a threshold of outage probability 𝒪_t, the probability ϵ should fulfill ϵ ≥ (1 − 𝒪_t). Applying this result in (37), we can easily obtain (35) by solving the inequality.

Case 2. The key issue of this case is to find out the relationship between and the primary user′s capacity penalty and outage probability. The derived result is summarized as below, which offers a criterion to configure the power P₂.

Corollary 2. Given a probability ϵ and a threshold of outage probability 𝒪_t, the condition for the secondary user to operate in Case 2 is

(38)

where

is given by (18).

Proof. The first criterion for the secondary user to operate in Case 2 is (32). Following the derivation in [18], we can easily justify that (32) is equivalent to

(39)

Moreover, provided the condition (32), the primary user will always deal with the interference as noise. The SNR-mean

should fulfill the condition (14) to ensure the primary user′s outage probability under the threshold 𝒪_t. Then,

should simultaneously fulfill the conditions (39) and (14), which leads to the result (38).

Once is determined by employing (38), we can calculate maximum of the secondary user′s power as .

Case 3. This case includes three issues: (1) to find the relationship between E(|a₂₁|²) and ϵ by solving (33); (2) to determine the scaling factor ℒ in (34); (3) provided the condition (33), Theorem 1 shows that the secondary user will suffer capacity outage for the case of |a₂₁|² > λ₁ | a₂₂|². Then, we should calculate the outage probability to the secondary user. Note that, in Case 3, the primary user does not suffer capacity outage.

Corollary 3. Given a probability ϵ, a necessary condition for (33) to be satisfied is

(40)

Proof. See the appendix.

Usually, the probability ϵ is expected to be sufficiently large, for example, ϵ > 90%. In this situation, we can use (40) to obtain γ₁₁ > 15 dB. It means a necessary condition for Case 3 to happen is that the primary user operates in a high-SNR range. Provided the condition (40), the secondary user can employ (A.1) to relate E(|a₂₁|²) to ϵ.

Using the scaling factor ℒ in (34) will result in capacity outage to the secondary user with the outage probability

(41)

If this outage probability is required to be no larger than a threshold 𝒪₁, we can obtain

(42)

This is one criterion to determine ℒ. Moreover, ℒ is also limited by the range given in (34). Applying that range in (42) results in

(43)

Then, we can conclude the following result.

Corollary 4. Given the threshold of outage probability 𝒪₁, a necessary condition for Case 3 to happen is (43).

Corollaries 3 and 4 provide an answer to the first two issues of Case 3. The last issue to concern is the probability Pr(|a₂₁|² > λ₁ | a₂₂|²) subject to the condition (33). The result is summarized as follows.

Corollary 5. Provided the condition (33), the probability for the event (|a₂₁|² > λ₁ | a₂₂|²) to happen is smaller than (1)/(γ₁₁ + 1).

Proof. The probability for the event (|a₂₁|² > λ₁ | a₂₂|²) to happen is given in (37), which can be represented into

(44)

Provided the condition (33), (A.2) gives the maximum of E(|a₂₁|²). Since (44) is an increasing function of E(|a₂₁|²), we can apply (A.2) into (44) and obtain

(45)

(46)

The discussion about Corollary 3 shows that γ₁₁ ≫ 1 is the necessary condition for Case 3. Therefore, the right hand of (46) approximates to (1)/(γ₁₁ + 1).

According to Corollaries 3–5, we summarize Case 3 as follows.

Step 1 .2. Utilize (40) and Corollary 5 to verify whether γ₁₁ fulfills the required condition. if true, go to Step 2.

Step 2. Utilize (43) and (A.2) to verify whether E(|a₂₁|²) is in the appropriate range; if true, go to Step 3;

Step 3. Utilize (42) to determine ℒ, and apply it in (34).

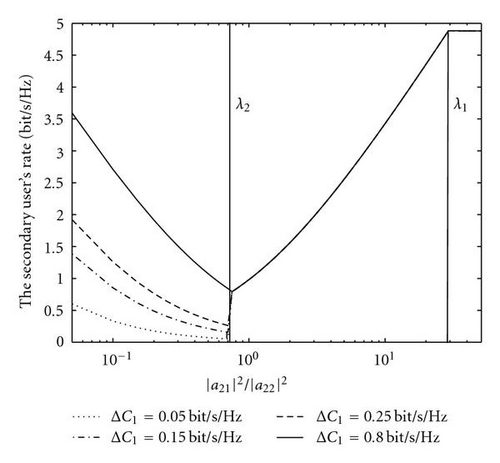
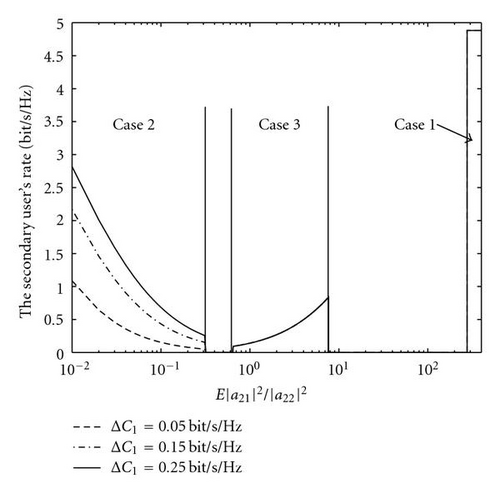
Next, we use a visual example to exhibit the performance. The system configuration is the same as the setup in Section 3.3. For the scenario with full multiuser CQI, Figure 5 shows the secondary user′s achievable rate as a function of the ratio |a₂₁|²/|a₂₂|². Calculation of the achievable rate follows the conclusion in Section 5.1. For the scenario with partial multiuser CQI, Figure 6 shows the secondary user′s achievable rate as a function of the ratio E(|a₂₁|²)/|a₂₂|². Calculation of the achievable rate follows the results presented in Corollaries 1–4 by setting the outage probability 𝒪_t = 𝒪₁ = 10% and the probability ϵ = 90%. It is observed that Case 1 will happen only for the condition E(|a₂₁|²)/|a₂₂|² > 300, which often does not hold in practice. Case 3 requires the primary user to operate at a SNR larger than 15 dB (see Corollary 3). However, in this case, the secondary user cannot gain more than 1 bit/sec/Hz at P₂/N_o = 16 dB. Finally, Case 2 shows a comparable performance with the corresponding scenario (|a₂₁|²/|a₂₂|² < λ₂) in Figure 5.

6. The TSMD Mode

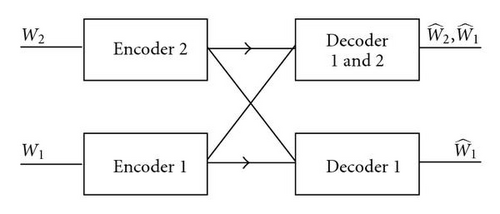
Figure 2(d) depicts the TSMD mode where each user knows the other′s codebook. Then, each user has the chance to decode the other user′s message so as to cancel the interference.

6.1. Capacity Results with Full Multiuser CQI

Capacity theorem about two-user GIC channel [11] has told us that the secondary user cannot reliably decode the primary user′s message for the channel condition |a₁₂ | <|a₁₁|. Hence, for the case of |a₁₂ | <|a₁₁|, the TSMD mode reduces to a special example of the PSMD mode.

For the channel condition |a₁₂ | ≥|a₁₁| and |a₂₁ | ≥|a₂₂|, the TSMD system becomes a compound multiple-access channel [10] whose capacity region is given by (3). In this case, the primary user does not need to pay capacity penalty, and thus the secondary user′s capacity is

(47)

The transmit power P₂ is limited only by the local power constraint.

For the channel condition |a₁₂ | ≥|a₁₁| and |a₂₁ | <|a₂₂|, the secondary user can access the primary spectrum without causing capacity penalty to the primary user. In this case, each user will decode the other′s message for interference cancelation, and thus the secondary user′s transmission rate is (47). Due to |a₂₁ | <|a₂₂|, we can easily justify that (47) equals to (27). If the primary user deals with the interference as noise, the TSMD mode reduces to the SSMD mode. Then, the secondary user′s transmission rate is (21), and the transmit power P₂ is limited by (11). According to Criteria 2&3, the secondary user′s achievable rate for the channel condition |a₁₂ | ≥|a₁₁| and |a₂₁ | <|a₂₂| is

(48)

6.2. The UCR Strategy with Partial Multiuser CQI

It has been shown in Section 6.1 that the TSMD mode reduces to the PSMD mode for the channel condition |a₁₂ | <|a₁₁|. Therefore, the UCR strategy here is proposed only for the condition |a₁₂ | ≥|a₁₁|.

Case 1 .1. Suppose

(49)

the secondary user will access the primary spectrum at the transmission rate

(50)

Equation(50) is produced by replacing the term γ₂₁ in (47) with (P₂ℒ)/(N_o) where ℒ>|a₂₂|².

Case 2 .2. Suppose

(51)

the UCR strategy is described as the following steps.

Step 1 .1.2. Utilize (14) to determine max (P₂) with respect to a given capacity penalty ΔC₁.

Step 2 .2. Calculate the following result which is produced by replacing P₂ in (21) with (14)

(52)

Step 3 .3. Calculate the following result which is produced by replacing the term γ₂₁ in (27) with (P₂ℒ)/(N_o) ()

(53)

Step 4 .4. Determine the secondary user′s transmission rate via .

6.3. Numerical Example

Considering |a₂₁| to be Rayleigh distributed, we derive the following results for Case 1 and Case 2, respectively.

Corollary 6. A sufficient condition for Case 1 to happen is

(54)

Proof. Equation (54) can be straightforwardly obtained through calculation of (49) and Pr(ℒ≤|a₂₁|²) ≤ ϵ.

Corollary 7. A sufficient condition for Case 2 to happen is

(55)

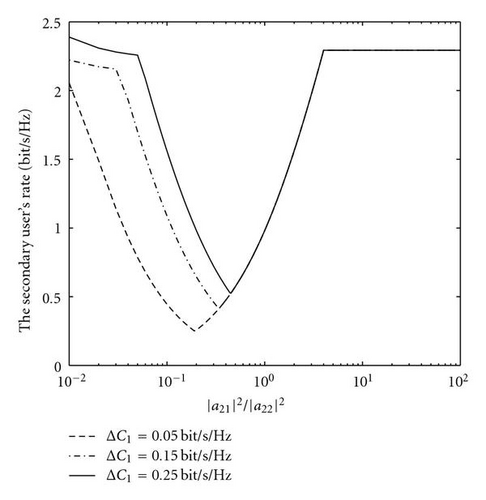
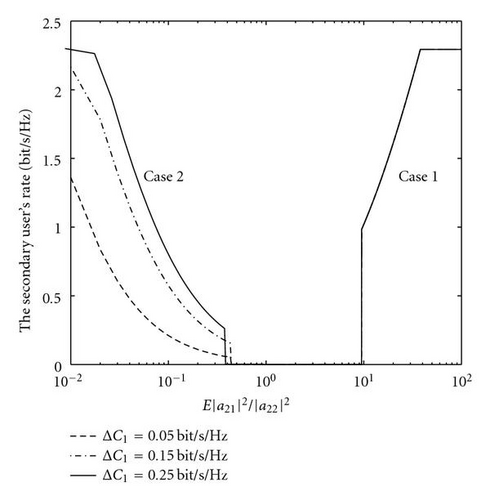
Proof. (55) can be straightforwardly obtained through calculation of (51) and Pr(ℒ≤|a₂₁|²) ≤ ϵ. Figures 7 and 8 show a visual example for scenarios with full or partial multiuser CQI, respectively. The system configuration is almost the same as the setup in Section 3.3, but we set |a₁₂|² = 4 to fulfill the condition |a₁₂ | >|a₁₁|. For the scenario with partial multiuser CQI, we set 𝒪_t = 10% and ϵ = 90% as an example. It is observed that Case 1– Case 2 in Figure 8 offers comparable performance with the corresponding scenario in Figure 7.

7. Conclusion

In this paper, we have investigated two-user Gaussian UCR systems by assuming the availability of full multiuser CQI or partial multiuser CQI. Provided full multiuser CQI, we have studied the fundamental relationship between the secondary user′s achievable rate C₂ and capacity penalty to the primary user ΔC₁ in four carefully classified UCR modes. For the scenario with partial multiuser CQI, we first established a new physical-layer model through exploitation of the location-aided approach. Then, new spectrum access and power allocation strategies have been investigated in terms of C₂, ΔC₁, and capacity outage probability. Numerical examples are provided to show the performance of the UCR with full multiuser CQI and the proposed approach with partial multiuser CQI.

Acknowledgments

The authors would like to thank the editor, Dr. Ronald Raulefs, and anonymous reviewers for their extremely constructive and supportive comments. This work has been performed in the framework of the ICT project ICT-217033 WHERE, which is partly funded by the European Union.

Appendix

Proof of Corollary 3

For the Rayleigh distribution, we can calculate

(A.1)

Using the first derivative of

with respect to

, we can find that

is an increasing function of

for the condition

(A.2)

and otherwise a decreasing function. Hence, we have

(A.3)

A necessary condition for (33) to be satisfied is

. Due to (γ₁₁)/(γ₁₁ + 1) < 1, it is necessary to have the following condition to be satisfied

(A.4)

Solving this inequality leads to (40).

References

1 Zhao Q. and Sadler B. M., A survey of dynamic spectrum access, IEEE Signal Processing Magazine. (2007) 24, no. 3, 79–89, 2-s2.0-34249728222, https://doi.org/10.1109/MSP.2007.361604.
Web of Science® Google Scholar
2 Goldsmith A., Jafar S. A., Maric I., and Srinivasa S., Breaking spectrum gridlock with cognitive radios: an information theoretic perspective, Proceedings of the IEEE. (2009) 97, no. 5, 894–914, 2-s2.0-67349259569, https://doi.org/10.1109/JPROC.2009.2015717.
Google Scholar
3 MitolaJ.III and MaguireG. Q.Jr., Cognitive radio: making software radios more personal, IEEE Personal Communications. (1999) 6, no. 4, 13–18, 2-s2.0-0033171330, https://doi.org/10.1109/98.788210.
Google Scholar
4 Marić I., Yates R. D., and Kramer G., Capacity of interference channels with partial transmitter cooperation, IEEE Transactions on Information Theory. (2007) 53, no. 10, 3536–3548, 2-s2.0-35148822625, https://doi.org/10.1109/TIT.2007.904792.
Google Scholar
5 Devroye N., Mitran P., and Tarokh V., Achievable rates in cognitive radio channels, IEEE Transactions on Information Theory. (2006) 52, no. 5, 1813–1827, 2-s2.0-33646045863, https://doi.org/10.1109/TIT.2006.872971.
Google Scholar
6 Wu W., Vishwanath S., and Arapostathis A., Capacity of a class of cognitive radio channels: interference channels with degraded message sets, IEEE Transactions on Information Theory. (2007) 53, no. 11, 4391–4399, 2-s2.0-36349034718, https://doi.org/10.1109/TIT.2007.907436.
Google Scholar
7 Gel′fand S. I. and Pinsker M. S., Coding for channel with random parameters, Problems of Control and Information Theory. (1980) 9, no. 1, 19–31, 2-s2.0-0019148101.
Google Scholar
8 Costa M. H. M., Writing on dirty paper, IEEE Transactions on Information Theory. (1983) IT-29, no. 3, 439–441, 2-s2.0-0020752342.
Google Scholar
9 Carleial A. B., Interference channels, IEEE Transactions on Information Theory. (1978) IT-24, no. 1, 60–70, 2-s2.0-0017918923.
Google Scholar
10 Sato H., The capacity of gaussian interferene channel under strong interference, IEEE Transactions on Information Theory. (1981) IT-27, no. 6, 786–788, 2-s2.0-0019635833.
Google Scholar
11 Kramer G., Outer bounds on the capacity of Gaussian interference channels, IEEE Transactions on Information Theory. (2004) 50, no. 3, 581–586, 2-s2.0-1842533560, https://doi.org/10.1109/TIT.2004.825249.
Web of Science® Google Scholar
12 Shang X., Kramer G., and Chen B., A new outer bound and the noisy-interference sum-rate capacity for Gaussian interference channels, IEEE Transactions on Information Theory. (2009) 55, no. 2, 689–699, 2-s2.0-61349193242, https://doi.org/10.1109/TIT.2008.2009793.
Google Scholar
13 Costa M. H. M. and El Gamal A. A., The capacity region of the discrete memoryless interference channel with strong interference, IEEE Transactions on Information Theory. (1987) IT-33, no. 5, 710–711, 2-s2.0-0023420374.
Google Scholar
14 Cover T. M. and Thomas J. A., Element of Information Theory, 2006, 2nd edition, John Wiley & Sons, New York, NY, USA.
Google Scholar
15 EU-ICT FP7 WHERE Project, http://www.ict-where.eu/.
Google Scholar
16 Xing Y., Mathur C. N., Haleem M. A., Chandramouli R., and Subbalakshmi K. P., Dynamic spectrum access with QoS and interference temperature constraints, IEEE Transactions on Mobile Computing. (2007) 6, no. 4, 423–432, 2-s2.0-33847718286, https://doi.org/10.1109/TMC.2007.50.
Google Scholar
17 Hoang A. T. and Liang Y.-C., A two-phase channel and power allocation scheme for cognitive radio networks, Proceedings of the IEEE 17th International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC ′06), September 2006, Helsinki, Finland, 2-s2.0-44949200033, https://doi.org/10.1109/PIMRC.2006.254371.
Google Scholar
18 Simon M. K. and Alouini M.-S., Digital Communication over Fading Channel, 2005, 2nd edition, John Wiley & Sons, Canada.
Google Scholar

Citing Literature

All articles

Underlay Cognitive Radio with Full or Partial Channel Quality Information

Abstract

1. Introduction

2. System Model and Preparation

2.1. Two-User UCR with Full Multiuser CQI

2.1.1. Two-User GIC with Strong Interference

2.1.2. Two-User GIC with Weak or Mixed Interference

2.1.3. Two-User Gaussian UCR

2.2. Two-User UCR with Partial Multiuser CQI

3. The Individual Decoding Mode

3.1. Capacity Results with Full Knowledge of CQI

3.2. The UCR Strategy with Partial Multiuser CQI

3.3. Numerical Example

4. The SSMD Mode

4.1. Capacity Results with Full Multiuser CQI

4.2. The UCR Strategy with Partial Multiuser CQI

5. The PSMD Mode

5.1. Capacity Results with Full Multiuser CQI

5.2. The UCR Strategy with Partial Multiuser CQI

5.3. Numerical Example

6. The TSMD Mode

6.1. Capacity Results with Full Multiuser CQI

6.2. The UCR Strategy with Partial Multiuser CQI

6.3. Numerical Example

7. Conclusion

Acknowledgments

Appendix

Proof of Corollary 3

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Underlay Cognitive Radio with Full or Partial Channel Quality Information

Abstract

1. Introduction

2. System Model and Preparation

2.1. Two-User UCR with Full Multiuser CQI

2.1.1. Two-User GIC with Strong Interference

2.1.2. Two-User GIC with Weak or Mixed Interference

2.1.3. Two-User Gaussian UCR

2.2. Two-User UCR with Partial Multiuser CQI

3. The Individual Decoding Mode

3.1. Capacity Results with Full Knowledge of CQI

3.2. The UCR Strategy with Partial Multiuser CQI

3.3. Numerical Example

4. The SSMD Mode

4.1. Capacity Results with Full Multiuser CQI

4.2. The UCR Strategy with Partial Multiuser CQI

5. The PSMD Mode

5.1. Capacity Results with Full Multiuser CQI

5.2. The UCR Strategy with Partial Multiuser CQI

5.3. Numerical Example

6. The TSMD Mode

6.1. Capacity Results with Full Multiuser CQI

6.2. The UCR Strategy with Partial Multiuser CQI

6.3. Numerical Example

7. Conclusion

Acknowledgments

Appendix

Proof of Corollary 3

References

Citing Literature

Figures

References

Related

Information