In the present review we survey the properties of a transcendental function of the Wright type, nowadays known as M-Wright function, entering as a probability density in a relevant class of self-similar stochastic processes that we generally refer to as time-fractional diffusion processes. Indeed, the master equations governing these processes generalize the standard diffusion equation by means of time-integral operators interpreted as derivatives of fractional order. When these generalized diffusion processes are properly characterized with stationary increments, the M-Wright function is shown to play the same key role as the Gaussian density in the standard and fractional Brownian motions. Furthermore, these processes provide stochastic models suitable for describing phenomena of anomalous diffusion of both slow and fast types.

1. Introduction

By time-fractional diffusion processes, we mean certain diffusion-like phenomena governed by master equations containing fractional derivatives in time whose fundamental solution can be interpreted as a probability density function (pdf) in space evolving in time. It is well known that, for the most elementary diffusion process, the Brownian motion, the master equation, is the standard linear diffusion equation whose fundamental solution is the Gaussian density with a spatial variance growing linearly in time. In such case we speak about normal diffusion, reserving the term anomalous diffusion when the variance grows differently. A number of stochastic models for explaining anomalous diffusion have been introduced in literature; among them we like to quote the fractional Brownian motion; see, for example, [1, 2], the Continuous Time Random Walk; see, for example, [3–6], the Lévy flights; see, for example, [7], the Schneider grey Brownian motion; see [8, 9], and, more generally, random walk models based on evolution equations of single and distributed fractional order in time and/or space; see, for example, [10–18].

In this survey paper we focus our attention on modifications of the standard diffusion equation, where the time can be stretched by a power law (t → t^α, 0 < α < 2) and the first-order time derivative can be replaced by a derivative of noninteger order β (0 < β ≤ 1). In these cases of generalized diffusion processes the corresponding fundamental solution still keeps the meaning of a spatial pdf evolving in time and is expressed in terms of a special function of the Wright type that reduces to the Gaussian when β = 1. This transcendental function, nowadays known as M-Wright function, will be shown to play a fundamental role for a general class of self-similar stochastic processes with stationary increments, which provide stochastic models for anomalous diffusion, as recently shown by Mura et al. [19–22].

In Section 2 we provide the reader with the essential notions and notations concerning the integral transforms and fractional calculus, which are necessary in the rest of the paper. In Section 3 we introduce in the complex plane ℂ the series and integral representations of the general Wright function denoted by W_λ,μ(z) and of the two related auxiliary functions F_ν(z), M_ν(z), which depend on a single parameter. In Section 4 we consider our auxiliary functions in real domain pointing out their main properties involving their integrals and their asymptotic representations. Mostly, we restrict our attention to the second auxiliary function, which we call M-Wright function, when its variable is in ℝ⁺ or in all of ℝ but extended in symmetric way. We derive a fundamental formula for the absolute moments of this function in ℝ⁺, which allows us to obtain its Laplace and Fourier transforms. In Section 5 we consider some types of generalized diffusion equations containing time partial derivatives of fractional order and we express their fundamental solutions in terms of the M-Wright functions evolving in time with a given self-similarity law. In Section 6 we stress how the M-Wright function emerges as a natural generalization of the Gaussian probability density for a class of self-similar stochastic processes with stationary increments, depending on two parameters (α, β). These processes are defined in a unique way by requiring the determination of any multipoint probability distribution and include the well-known standard and fractional Brownian motion. We refer to this class as the generalized grey Brownian motion (ggBm), because it generalizes the grey Brownian motion (gBm) introduced by Schneider [8, 9]. Finally, a short concluding discussion is drawn. In Appendix A we derive the fundamental solution of the time-fractional diffusion equation. In Appendix B we outline the relevance of the M-Wright function in time-fractional drift processes entering as subordinators in time-fractional diffusion.

2. Notions and Notations

2.1. Integral Transforms Pairs

In our analysis we will make extensive use of integral transforms of Laplace, Fourier, and Mellin types; so we first introduce our notation for the corresponding transform pairs. We do not point out the conditions of validity and the main rules, since they are given in any textbook on advanced mathematics.

Let

()

be the Laplace transform of a sufficiently well-behaved function f(r) with r ∈ ℝ⁺, s ∈ ℂ, and let

()

be the inverse Laplace transform, where Br denotes the so-called Bromwich path, a straight line parallel to the imaginary axis in the complex s-plane. Denoting by

the justaposition of the original function f(r) with its Laplace transform

, the Laplace transform pair reads

()

Let

()

be the Fourier transform of a sufficiently well-behaved function f(x) with x ∈ ℝ, κ ∈ ℝ, and let

()

be the inverse Fourier transform. Denoting by

the justaposition of the original function f(x) with its Fourier transform

, the Fourier transform pair reads

()

Let

()

be the Mellin transform of a sufficiently well-behaved function f(r) with r ∈ ℝ⁺, s ∈ ℂ, and let

()

be the inverse Mellin transform. Denoting by

the justaposition of the original function f(r) with its Mellin transform f^*(s), the Mellin transform pair reads

()

2.2. Essentials of Fractional Calculus with Support in ℝ⁺

Fractional calculus is the branch of mathematical analysis that deals with pseudodifferential operators that extend the standard notions of integrals and derivatives to any positive noninteger order. The term fractional is kept only for historical reasons. Let us restrict our attention to sufficiently well-behaved functions f(t) with support in ℝ⁺. Two main approaches exist in the literature of fractional calculus to define the operator of derivative of noninteger order for these functions, referred to Riemann-Liouville and to Caputo. Both approaches are related to the so-called Riemann-Liouville fractional integral defined for any order μ > 0 as

()

We note the convention

(Identity) and the semigroup property

()

The fractional derivative of order μ > 0 in the Riemann-Liouville sense is defined as the operator

which is the left inverse of the Riemann-Liouville integral of order μ (in analogy with the ordinary derivative), that is,

()

If m denotes the positive integer such that m − 1 < μ ≤ m, we recognize, from (2.11) and (2.12),

hence,

()

For completeness we define

On the other hand, the fractional derivative of order μ > 0 in the Caputo sense is defined as the operator such that ; hence,

()

We note the different behavior of the two derivatives in the limit μ → (m − 1) ⁺. In fact,

()

where the limit for t → 0⁺ is taken after the operation of derivation.

Furthermore, recalling the Riemann-Liouville fractional integral and derivative of the power law for t > 0,

()

we find the relationship between the two types of fractional derivative

()

We note that the Caputo definition for the fractional derivative incorporates the initial values of the function and of its integer derivatives of lower order. The subtraction of the Taylor polynomial of degree m − 1 at t = 0⁺ from f(t) is a sort of regularization of the fractional derivative. In particular, according to this definition, the relevant property that the derivative of a constant is zero is preserved for the fractional derivative.

Let us finally point out the rules for the Laplace transform with respect to the fractional integral and the two fractional derivatives. These rules are expected to properly generalize the well-known rules for standard integrals and derivatives.

For the Riemann-Liouville fractional integral, we have

()

For the Caputo fractional derivative, we consequently get

()

where

. The corresponding rule for the Riemann-Liouville fractional derivative is more cumbersome and it reads

()

where the limit for t → 0⁺ is understood to be taken after the operations of fractional integration and derivation. As soon as all the limiting values f^(k)(0⁺) are finite and m − 1 < μ < m, formula (2.20) for the Riemann-Liouville derivative is simplified into

()

In the special case f^(k)(0⁺) = 0 for k = 0,1, m − 1, we recover the identity between the two fractional derivatives. The Laplace transform rule (2.19) was practically the key result of Caputo [23, 24] in defining his generalized derivative in the late sixties. The two fractional derivatives have been well discussed in the 1997 survey paper by Gorenflo and Mainardi [25]; see also [26], and in the 1999 book by Podlubny [27]. In these references the authors have pointed out their preference for the Caputo derivative in physical applications where initial conditions are usually expressed in terms of finite derivatives of integer order.

For further reading on the theory and applications of fractional calculus, we recommend the recent treatise by Kilbas et al. [28].

3. The Functions of the Wright Type

3.1. The General Wright Function

The Wright function, which we denote by W_λ,μ,(z), is so named in honor of E. Maitland Wright, the eminent British mathematician, who introduced and investigated this function in a series of notes starting from 1933 in the framework of the asymptotic theory of partitions; see [29–31]. The function is defined by the series representation, convergent in the whole z-complex plane

()

Originally, Wright assumed that λ ≥ 0, and, only in 1940 [32], he considered −1 < λ < 0. We note that in Chapter 18 of Vol. 3 of the handbook of the Bateman Project [33], devoted to Miscellaneous Functions, presumably for a misprint, the parameter λ of the Wright function is restricted to be nonnegative. When necessary, we propose to distinguish the Wright functions in two kinds according to λ ≥ 0 (first kind) and −1 < λ < 0 (second kind).

For more details on Wright functions the reader can consult, for example, [34–41] and references therein.

The integral representation of the Wright function reads

()

where Ha denotes the Hankel path. We remind that the Hankel path is a loop that starts from −∞ along the lower side of the negative real axis, encircles the circular area around the origin with radius ϵ → 0 in the positive sense, and ends at −∞ along the upper side of the negative real axis. The equivalence of the series and integral representations is easily proved using Hankel formula for the Gamma function

()

and performing a term-by-term integration. In fact,

()

It is possible to prove that the Wright function is entire of order 1/(1 + λ); hence, it is of exponential type only if λ ≥ 0 (which corresponds to Wright function of the first kind). The case λ = 0 is trivial since W_0,μ(z) = e^z/Γ(μ), provided that μ ≠ 0, −1, −2, ….

3.2. The Auxiliary Functions of the Wright Type

Mainardi, in his first analysis of the time-fractional diffusion equation [42, 43], aware of the Bateman handbook [33], but not yet of the 1940 paper by Wright [32], introduced the two (Wright-type) entire auxiliary functions,

()

interrelated through

()

As a matter of fact, functions F_ν(z) and M_ν(z) are particular cases of the Wright function of the second kind W_λ,μ(z) by setting λ = −ν and μ = 0 or μ = 1, respectively.

Hereafter, we provide the series and integral representations of the two auxiliary functions derived from the general formulas (3.1) and (3.2), respectively.

The series representations for the auxiliary functions read

()

The second series representations in (3.7)-(3.8) have been obtained by using the reflection formula for the Gamma function Γ(ζ) Γ(1 − ζ) = π/sin πζ.

As an exercise, the reader can directly prove that the radius of convergence of the power series in (3.7)-(3.8) is infinite for 0 < ν < 1 without being aware of Wright′s results, as it was shown independently by Mainardi [42]; see also [27].

Furthermore, we have F_ν(0) = 0 and M_ν(0) = 1/Γ(1 − ν). We note that relation (3.6) between the two auxiliary functions can be easily deduced from (3.7)-(3.8), by using the basic property of the Gamma function Γ(ζ + 1) = ζ Γ(ζ).

The integral representations for the auxiliary functions read

()

We note that relation (3.6) can be obtained also from (3.9)-(3.10) with an integration by parts. In fact,

()

The equivalence of the series and integral representations is easily proved by using the Hankel formula for the Gamma function and performing a term-by-term integration.

3.3. Special Cases

Explicit expressions of F_ν(z) and M_ν(z) in terms of known functions are expected for some particular values of ν. Mainardi and Tomirotti [43] have shown that for ν = 1/q, where q ≥ 2 is a positive integer, the auxiliary functions can be expressed as a sum of simpler (q − 1) entire functions. In the particular cases q = 2 and q = 3, we find

()

where Ai denotes the Airy function.

Furthermore, it can be proved that M_1/q(z) satisfies the differential equation of order q − 1

()

subjected to the q − 1 initial conditions at z = 0, derived from (3.14), such that

()

with h = 0, 1, …, q − 2. We note that, for q ≥ 4, (3.14) is akin to the hyper-Airy differential equation of order q − 1; see, for example, [44]. Consequently, the auxiliary function M_ν(z) could be considered a sort of generalized hyper-Airy function. However, in view of further applications in stochastic processes, we prefer to consider it as a natural (fractional) generalization of the Gaussian function, similarly as the Mittag-Leffler function is known to be the natural (fractional) generalization of the exponential function.

To stress the relevance of the auxiliary function M_ν(z), it was also suggested the special name M-Wright function, a terminology that has been followed in literature to some extent.

Some authors including Podlubny [27], Gorenflo et al. [34, 35], Hanyga [45], Balescu [46], Chechkin et al. [12], Germano et al. [47], and Kiryakova [48, 49] refer to the M-Wright function as the Mainardi function. It was Professor Stanković, during the presentation of the paper by Mainardi and Tomirotti [43] at the Conference of Transform Methods and Special Functions, Sofia 1994, who informed Mainardi, being aware only of the Bateman Handbook [33], that the extension for −1 < λ < 0 had been already made just by Wright himself in 1940 [32], following his previous papers published in the thirties. Mainardi, in the paper [50] devoted to the 80th birthday of Prof. Stanković, used the occasion to renew his personal gratitude to Prof. Stanković for this earlier information that led him to study the original papers by Wright and work also in collaboration on the functions of the Wright type for further applications; see, for example, [34, 35, 51].

Moreover, the analysis of the limiting cases ν = 0 and ν = 1 requires special attention. For ν = 0 we easily recognize from the series representations (3.7)-(3.8)

()

The limiting case ν = 1 is singular for both auxiliary functions as expected from the definition of the general Wright function when λ = −ν = −1. Later we will deal with this singular case for the M-Wright function when the variable is real and positive.

4. Properties and Plots of the Auxiliary Wright Functions in Real Domain

Let us state some relevant properties of the auxiliary Wright functions, with special attention to the M_ν function in view of its role in time-fractional diffusion processes.

4.1. Exponential Laplace Transforms

We start with the Laplace transform pairs involving exponentials in the Laplace domain. These were derived by Mainardi in his earlier analysis of the time-fractional diffusion equation; see, for example, [42, 52],

()

We note that the inversion of the Laplace transform of the exponential exp (−s^ν) is relevant since it yields for any ν ∈ (0,1) the unilateral extremal stable densities in probability theory, denoted by

in [53]. As a consequence, the nonnegativity of both auxiliary Wright functions when their argument is positive is proved by the Bernstein theorem. We refer to Feller′s treatise [54, 55] for Laplace transforms, stable densities and Bernstein theorem. The Laplace transform pair in (4.1) has a long history starting from a formal result by Humbert [56] in 1945, of which Pollard [57] provided a rigorous proof one year later. Then, in 1959 Mikusiński [58] derived a similar result on the basis of his theory of operational calculus. In 1975, albeit unaware of the previous results, Buchen and Mainardi [59] derived the result in a formal way. We note that all the above authors were not informed about the Wright functions. To our actual knowledge the former author who derived the Laplace transforms pairs (4.1)-(4.2) in terms of Wright functions of the second kind was Stanković in 1970; see [39].

Hereafter we would like to provide two independent proofs of (4.1) carrying out the inversion of exp (−s^ν), either by the complex Bromwich integral formula following [42], or by the formal series method following [59]. Similarly we can act for the Laplace transform pair (4.2). For the complex integral approach we deform the Bromwich path Br into the Hankel path Ha, that is equivalent to the original path, and we set σ = sr. Recalling the integral representation (3.9) for the F_ν function and (3.6), we get

()

Expanding in power series the Laplace transform and inverting term by term, we formally get

()

where now we have used the series representation (3.7) for the function F_ν along with the relationship formula (3.6).

4.2. Asymptotic Representation for Large Argument

Let us point out the asymptotic behavior of the function M_ν(r) when r → ∞. Choosing a variable r/ν rather than r, the computation of the desired asymptotic representation by the saddle-point approximation is straightforward. Mainardi and Tomirotti [43] have obtained

()

The above evaluation is consistent with the first term in the asymptotic series expansion provided by Wright with a cumbersome and formal procedure for his general function W_λ,μ when −1 < λ < 0; see [32]. In 1999 Wong and Zhao have derived asymptotic expansions of the Wright functions of the first and second kind in the whole complex plane following a new method for smoothing Stokes′ discontinuities; see [40, 41], respectively.

We note that, for ν = 1/2 as (4.5) provides the exact result consistent with (3.12),

()

We also note that in the limit ν → 1⁻ the function M_ν(r) tends to the Dirac generalized function δ(r − 1), as can be recognized also from the Laplace transform pair (4.1).

4.3. Absolute Moments

From the above considerations we recognize that, for the M-Wright functions, the following rule for absolute moments in ℝ⁺ holds

()

In order to derive this fundamental result, we proceed as follows on the basis of the integral representation (3.10):

()

Above we have legitimized the exchange between integrals and used the identity

()

along with the Hankel formula of the Gamma function. Analogously, we can compute all the moments of F_ν(r) in ℝ⁺.

4.4. The Laplace Transform of the M-Wright Function

Let the Mittag-Leffler function be defined in the complex plane for any ν ≥ 0 by the following series and integral representation; see, for example, [33, 60]:

()

Such function is entire of order 1/α for α > 0 and reduces to the function exp (z) for ν > 0 and to 1/(1 − z) for ν = 0. We recall that the Mittag-Leffler function for ν > 0 plays fundamental roles in applications of fractional calculus like fractional relaxation and fractional oscillation; see, for example, [25, 26, 61, 62], so that it could be referred as the Queen function of fractional calculus. Recently, numerical routines for functions of Mittag-Leffler type have been provided, e.g., by Freed et al. [63], Gorenflo et al. [64] (with MATHEMATICA), Podlubny [65] (with MATLAB), Seybold and Hilfer [66].

We now point out that the M-Wright function is related to the Mittag-Leffler function through the following Laplace transform pair:

()

For the reader′s convenience, we provide a simple proof of (4.11) by using two different approaches. We assume that the exchanges between integrals and series are legitimate in view of the analyticity properties of the involved functions. In the first approach we use the integral representations of the two functions obtaining

()

In the second approach we develop in series the exponential kernel of the Laplace transform and we use the expression (4.7) for the absolute moments of the M-Wright function arriving to the following series representation of the Mittag-Leffler function:

()

We note that the transformation term by term of the series expansion of the M-Wright function is not legitimate because the function is not of exponential order; see [67]. However, this procedure yields the formal asymptotic expansion of the Mittag-Leffler function E_ν(−s) as s → ∞ in a sector around the positive real axis; see, for example, [33, 60], that is,

()

4.5. The Fourier Transform of the Symmetric M-Wright Function

The M-Wright function, extended on the negative real axis as an even function, is related to the Mittag-Leffler function through the following Fourier transform pair:

()

Below, we prove the equivalent formula

()

For the proof it is sufficient to develop in series the cosine function and use formula (4.7) for the absolute moments of the M-Wright function:

()

4.6. The Mellin Transform of the M-Wright Function

It is straightforward to derive the Mellin transform of the M-Wright function using result (4.7) for the absolute moments of the M-Wright function. In fact, setting δ = s − 1 in (4.7), by analytic continuation it follows:

()

4.7. Plots of the Symmetric M-Wright Function

It is instructive to show the plots of the (symmetric) M-Wright function on the real axis for some rational values of the parameter ν. In order to have more insight of the effect of the parameter itself on the behavior close to and far from the origin, we adopt both linear and logarithmic scale for the ordinates.

In Figures 1 and 2 we compare the plots of the M_ν(x)-Wright functions in−5 ≤ x ≤ 5 for some rational values of ν in the ranges ν ∈ [0,1/2] and ν ∈ [1/2,1], respectively. In Figure 1 we see the transition from exp (−|x|) for ν = 0 to for ν = 1/2, whereas in Figure 2 we see the transition from to the delta functions δ(x ± 1) for ν = 1. Because of the two symmetrical humps for 1/2 < ν ≤ 1, the M_ν function appears bimodal with the characteristic shape of the capital letter M.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Plots of the symmetric M_ν-Wright function with ν = 0,1/8,1/4,3/8,1/2 for−5 ≤ x ≤ 5: (a) linear scale, (b) logarithmic scale.

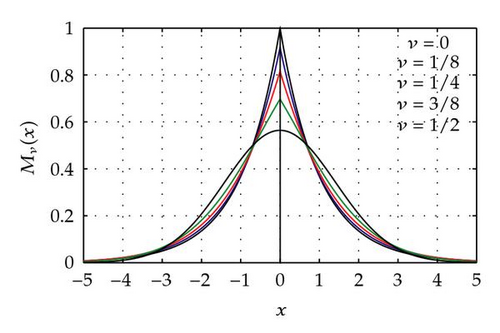
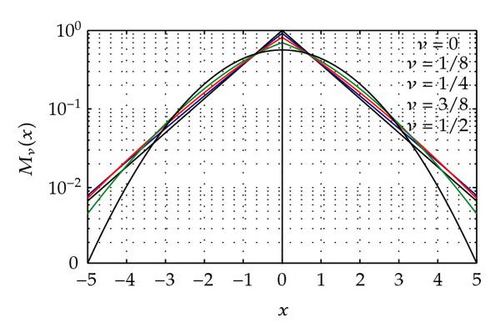
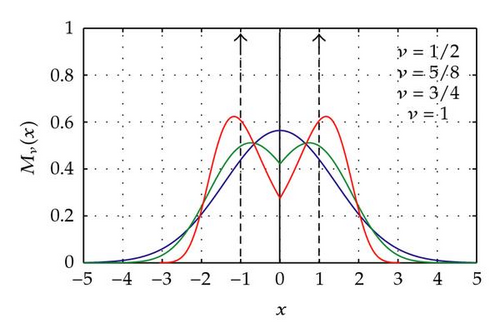
In plotting M_ν(x) at fixed ν for sufficiently large x, the asymptotic representation (4.5)-(4.6) is useful since, as x increases, the numerical convergence of the series in (3.8) decreases up to being completely inefficient: henceforth, the matching between the series and the asymptotic representation is relevant and followed by Mainardi and associates; see, for example, [38, 51, 53, 68]. However, as ν → 1⁻, the plotting remains a very difficult task because of the high peak arising around x = ±1. For this we refer the reader to the 1997 paper by Mainardi and Tomirotti [69], where a variant of the saddle point method has been successfully used to properly depict the transition to the delta functions δ(x ± 1) as ν approaches 1. For the numerical point of view we like to highlight the recent paper by Luchko [70], where algorithms are provided for computation of the Wright function on the real axis with prescribed accuracy.

4.8. The 𝕄-Wright Function in Two Variables

In view of the time-fractional diffusion processes that will be considered in the next sections, it is worthwhile to introduce the function in the two variables

()

which defines a spatial probability density in x evolving in time t with self-similarity exponent H = ν. Of course for x ∈ ℝ we have to consider the symmetric version obtained from (4.19) multiplying by 1/2 and replacing x by |x|.

Hereafter we provide a list of the main properties of this function, which can be derived from Laplace and Fourier transforms of the corresponding M-Wright function in one variable.

From (4.2) we derive the Laplace transform of 𝕄_ν(x, t) with respect to t ∈ ℝ⁺ as

()

From (4.10) we derive the Laplace transform of 𝕄_ν(x, t) with respect to x ∈ ℝ⁺ as

()

From (4.15) we derive the Fourier transform of 𝕄_ν(|x | , t) with respect to x ∈ ℝ as

()

Moreover, using the Mellin transform, Mainardi et al. [71] derived the following integral formula:

()

Special cases of the 𝕄-Wright function are simply derived for ν = 1/2 and ν = 1/3 from the corresponding ones in the complex domain; see (3.12)-(3.13). We devote particular attention to the case ν = 1/2 for which we get from (4.6) the Gaussian density in ℝ:

()

For the limiting case ν = 1 we obtain

()

5. Fractional Diffusion Equations

Let us now consider a variety of diffusion-like equations starting from the standard diffusion equation whose fundamental solutions are expressed in terms of the M-Wright function depending on space and time variables. The two variables, however, turn out to be related through a self-similarity condition.

5.1. The Standard Diffusion Equation

The standard diffusion equation for the field u(x, t) with initial condition u(x, 0) = u₀(x) is

()

where K₁ is a suitable diffusion coefficient of dimensions [K₁] = [L] ²[T] ⁻¹ = cm²/sec. This initial-boundary value problem can be easily shown to be equivalent to the Volterra integral equation

()

It is well known that the fundamental solution (usually referred as the Green function), which is the solution corresponding to u₀(x) = δ(x), is the Gaussian probability density evolving in time with variance (mean square displacement) proportional to time. In our notation we have

()

This variance law characterizes the process of normal diffusion as it emerges from Einstein′s approach to Brownian motion (Bm); see, for example, [72].

In view of future developments, we rewrite the Green function in terms of the M-Wright function by recalling (3.12), that is,

()

From the self-similarity of the Green function in (5.3) or (5.5), we are led to write

()

where H = 1/2 is the similarity (or Hurst) exponent and

acts as the similarity variable. We refer to the one-variable function 𝒢₁(ξ) as the reduced Green function.

5.2. The Stretched-Time Standard Diffusion Equation

Let us now stretch the time variable in (5.1) by replacing t with t^α where 0 < α < 2. We have

()

where K_α is a sort of stretched diffusion coefficient of dimensions [K_α] = [L] ²[T] ^−α = cm²/sec^α. It is easy to recognize that such equation is akin to the standard diffusion equation but with a diffusion coefficient depending on time; K₁(t) = αt^α−1K_α. In fact, using the rule

()

we have

()

The integral form corresponding to (5.7)—(5.9) reads

()

The corresponding fundamental solution is the stretched-time Gaussian

()

The corresponding variance

()

is characteristic of a general process of anomalous diffusion, precisely of slow diffusion for 0 < α < 1, and of fast diffusion for 1 < α < 2.

5.3. The Time-Fractional Diffusion Equation

In literature there exist two forms of the time-fractional diffusion equation of a single order, one with Riemann-Liouvile derivative and one with Caputo derivative. These forms are equivalent if we refer to the standard initial condition u(x, 0) = u₀(x), as shown in [73].

Taking a real number β ∈ (0,1), the time-fractional diffusion equation of order β in the Riemann-Liouville sense reads

()

whereas in the Caputo sense reads

()

where K_β is a sort of fractional diffusion coefficient of dimensions [K_β] = [L] ²[T] ^−β = cm²/sec^β. Like for diffusion equations of integer order (5.1) and (5.7)-(5.9), we consider the equivalent integral equation corresponding to our fractional diffusion equations (5.13)-(5.14) as

()

The Green function 𝒢_β(x, t) for the equivalent (5.13)–(5.15) can be expressed, also in this case, in terms of the M-Wright function, as shown in Appendix A by adopting two different approaches, as follows:

()

The corresponding variance can be promptly obtained from the general formula (5.5) for the absolute moment of the M-Wright function. In fact, using (5.5) and (5.16) and after an obvious change of variable, we obtain

()

As a consequence, for 0 < β < 1 the variance is consistent with a process of slow diffusion with similarity exponent H = β/2. For further reading on time-fractional diffusion equations and their solutions the reader is referred, among others, to [38, 51, 53] and [74, 75].

5.4. The Stretched Time-Fractional Diffusion Equation

In the fractional diffusion equation (5.13), let us stretch the time variable by replacing t with t^α/β where 0 < α < 2 and 0 < β ≤ 1. We have

()

namely,

()

where K_αβ is a sort of stretched diffusion coefficient of dimensions [K_αβ] = [L] ²[T] ^−α = cm²/sec^α that reduces to K_α if β = 1 and to K_β if α = β. Integration of (5.19) gives the corresponding integral equation [21]

()

whose Green function 𝒢_αβ(x, t) is

()

with variance

()

As a consequence, the resulting process turns out to be self-similar with Hurst exponent H = α/2 and a variance law consistent with both slow diffusion if 0 < α < 1 and fast diffusion if 1 < α < 2. We note that the parameter β does explicitly enter in the variance law (5.22) only as in the determination of the multiplicative constant.

It is straightforward to note that the evolution equations of this process reduce to those for time-fractional diffusion if α = β < 1, for stretched diffusion if α ≠ 1 and β = 1, and finally for standard diffusion if α = β = 1.

6. Fractional Diffusion Processes with Stationary Increments

We have seen that any Green function associated to the diffusion-like equations considered in the previous section can be interpreted as the time-evolving one-point pdf of certain self-similar stochastic processes. However, in general, it is not possible to define a unique (self-similar) stochastic process because the determination of any multipoint probability distribution is required; see, for example, [22].

In other words, starting from a master equation which describes the dynamic evolution of a probability density function f(x, t), it is always possible to define an equivalence class of stochastic processes with the same marginal density function f(x, t). All these processes provide suitable stochastic representations for the starting equation. It is clear that additional requirements may be stated in order to uniquely select the probabilistic model.

For instance, considering (5.19), the additional requirement of stationary increments, as shown by Mura et al.; see [19–22], can lead to a class {B_α,β(t), t ≥ 0}; called “generalized” grey Brownian motion (ggBm), which, by construction, is made up of self-similar processes with stationary increments and Hurst exponent H = α/2. Thus {B_α,β(t), t ≥ 0} is a special class of H-sssi processes, which provide non-Markovian stochastic models for anomalous diffusion, of both slow type (0 < α < 1) and fast type (1 < α < 2). According to a common terminology, H-sssi stands for H-self-similar-stationary-increments, see for details [2].

The ggBm includes some well known processes, so that it defines an interesting general theoretical framework. The fractional Brownian motion (fBm) appears for β = 1 and is associated with (5.7); the grey Brownian motion (gBm), defined by Schneider [8, 9], corresponds to the choice α = β, with 0 < β < 1, and is associated to (5.13), (5.14), or (5.15); finally, the standard Brownian motion (Bm) is recovered by setting α = β = 1 being associated to (5.1). We should note that only in the particular case of Bm the corresponding process is Markovian.

In Figure 3 we present a diagram that allows to identify the elements of the ggBm class. The top region 1 < α < 2 corresponds to the domain of fast diffusion with long-range dependence. We remind that a self-similar process with stationary increments is said to possess long-range dependence if the autocorrelation function of the increments tends to zero like a power function and such that it does not result integrable, see for details [2]. In this domain the increments of the process B_α,β(t) are positively correlated, so that the trajectories tend to be more regular (persistent). It should be noted that long-range dependence is associated to a non-Markovian process which exhibits long-memory properties. The horizontal line α = 1 corresponds to processes with uncorrelated increments, which model various phenomena of normal diffusion. For α = β = 1 we recover the Gaussian process of the standard Brownian motion. The Gaussian process of the fractional Brownian motion is identified by the vertical line β = 1. The bottom region 0 < α < 1 corresponds to the domain of slow diffusion. The increments of the corresponding process B_α,β(t) turn out to be negatively correlated and this implies that the trajectories are strongly irregular (antipersistent motion); the increments form a stationary process which does not exhibit long-range dependence. Finally, the diagonal line (α = β) represents the Schneider grey Brownian motion (gBm).

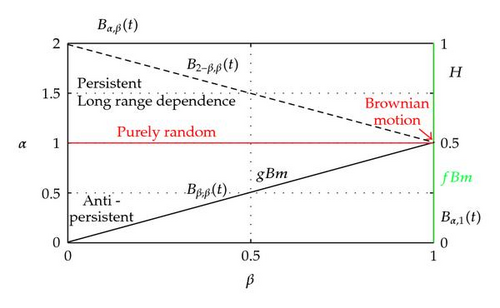
Here we want to define the ggBm by making use of the Kolmogorov extension theorem and the properties of the M-Wright function. According to Mura and Pagnini [21], the generalized grey Brownian motion B_α,β(t) is a stochastic process defined in a certain probability space such that its finite-dimensional distributions are given by

()

with

()

and covariance matrix

()

The covariance matrix (6.3) characterizes the typical dependence structure of a self-similar process with stationary increments and Hurst exponent H = α/2; see, for example, [2].

Using (4.23), for n = 1, (6.1) reduces to

()

This means that the marginal density function of the ggBm is indeed the fundamental solution (5.21) of (5.18)-(5.19) with K_αβ = 1. Moreover, because M₁(τ) = δ(τ − 1), for β = 1, putting γ_α,1 ≡ γ_α, we have that (6.1) provides the Gaussian distribution of the fractional Brownian motion

()

which finally reduces to the standard Gaussian distribution of Brownian motion as α = 1.

By the definition used above, it is clear that, fixed β, B_α,β(t) is characterized only by its covariance structure, as shown by Mura et al. [20, 21]. In other words, the ggBm, which is not Gaussian in general, is an example of a process defined only through its first and second moments, which indeed is a remarkable property of Gaussian processes. Consequently, the ggBm appears to be a direct generalization of Gaussian processes, in the same way as the M-Wright function is a generalization of the Gaussian function.

7. Concluding Discussion

In this review paper we have surveyed a quite general approach to derive models for anomalous diffusion based on a family of time-fractional diffusion equations depending on two parameters: α ∈ (0,2), β ∈ (0,1].

The unifying topic of this analysis is the so-called M-Wright function by which the fundamental solutions of these equations are expressed. Such function is shown to exhibit fundamental analytical properties that were properly used in recent papers for characterizing and simulating a general class of self-similar stochastic processes with stationary increments including fractional Brownian motion and grey Brownian motion.

In this respect, the M-Wright function emerges to be a natural generalization of the Gaussian density to model diffusion processes, covering both slow and fast anomalous diffusion and including non-Markovian property. In particular, it turns out to be the main function for the special H-sssi class of stochastic processes (which are self-similar with stationary increments) governed by a master equation of fractional type.

Acknowledgments

This work has been carried out in the framework of the research project Fractional Calculus Modelling (http://www.fracalmo.org/). The authors are grateful to V. Kiryakova, R. Gorenflo and the anonymous referees for useful comments.

Appendices

A. The Fundamental Solution of the Time-Fractional Diffusion Equation

The fundamental solution 𝒢_β(x, t) for the time-fractional diffusion equation can be obtained by applying in sequence the Fourier and Laplace transforms to any form chosen among (5.13)–(5.15) with the initial condition 𝒢_β(x, 0⁺) = u₀(x) = δ(x). Let us devote our attention to the integral form (5.15) using nondimensional variables by setting K_β = 1 and adopting the notation for the fractional integral (2.10). Then, our Cauchy problem reads

()

In the Fourier-Laplace domain, after applying formula (2.18) for the Laplace transform of the fractional integral and observing

; see, for example, [76], we get

()

from which

()

To determine the Green function 𝒢_β(x, t) in the space-time domain we can follow two alternative strategies related to the order in carrying out the inversions in (A.3).

(S1)
Invert the Fourier transform getting and then invert the remaining Laplace transform.
(S2)
Invert the Laplace transform getting and then invert the remaining Fourier transform.

Strategy (S1) Recalling the Fourier transform pair

()

and setting a = s^β−1, b = s^β, we get

()

Strategy (S2) Recalling the Laplace transform pair

()

and setting c = κ², we have

()

Both strategies lead to the result

()

consistent with (5.16). Here we have used the 𝕄-Wright function, introduced in Section 4, and its properties related to the Laplace transform pair (4.20) for inverting (A.5) and the Fourier transform pair (4.22) for inverting (A.7).

B. The Fundamental Solution of the Time-Fractional Drift Equation

Let us finally note that the M-Wright function does appear also in the fundamental solution of the time-fractional drift equation. Writing this equation in nondimensional form and adopting the Caputo derivative, we have

()

where 0 < β < 1 and u(x, 0⁺) = u₀(x). When u₀(x) = δ(x), we obtain the fundamental solution (Green function) that we denote by

. Following the approach of Appendix A, we show that

()

which for β = 1 reduces to the right running pulse δ(x − t) for x > 0.

In the Fourier-Laplace domain, after applying formula (2.19) for the Laplace transform of the Caputo fractional derivative and observing ; see, for example, [76], we get

()

from which

()

Like in Appendix A, to determine the Green function

in the space-time domain we can follow two alternative strategies related to the order in carrying out the inversions in (B.4).

(S1)
Invert the Fourier transform getting and then invert the remaining Laplace transform.
(S2)
Invert the Laplace transform getting and then invert the remaining Fourier transform.

Strategy (S1) Recalling the Fourier transform pair

()

and setting a = s^β−1, b = s^β, we get

()

Strategy (S2) Recalling the Laplace transform pair

()

and setting c = −iκ, we have

()

Both strategies lead to the result (B.2). In view of (4.1) we also recall that the M-Wright function is related to the unilateral extremal stable density of index

. Then, using our notation stated in [53] for stable densities, we write our Green function as

()

To conclude this Appendix, let us briefly discuss the above results in view of their relevance in fractional diffusion processes following the recent paper by Gorenflo and Mainardi [77]. Equation (B.1) describes the evolving sojourn probability density of the positively oriented time-fractional drift process of a particle, starting in the origin at the instant zero. It has been derived in [77] as a properly scaled limit for the evolution of the counting number of the Mittag-Leffler renewal process (the fractional Poisson process). It can be given in several forms, and often it is cited as the subordinator (producing the operational time from the physical time) for space-time-fractional diffusion as in the form (B.9). For more details see [3], where simulations of space-time-fractional diffusion processes have been considered as composed by time-fractional and space-fractional diffusion processes.

This analysis can be compared to that described with a different language in papers by Meerschaert et al. [4, 78]. Recently, a more exhaustive analysis has been given by Gorenflo [79].

References

1 Mandelbrot B. B. and Van Ness J. W., Fractional Brownian motions, fractional noises and applications, SIAM Review. (1968) 10, 422–437, MR0242239, https://doi.org/10.1137/1010093, ZBL0179.47801.
10.1137/1010093
Web of Science® Google Scholar
2 Taqqu M. S., P. Doukan, G. Oppenheim, and M. S. Taqqu, Fractional Brownian motion and long-range dependence, Theory and Applications of Long-Range Dependence, 2003, Birkhäuser, Boston, Mass, USA, 5–38, MR1956042, ZBL1039.60041.
Google Scholar
3 Gorenflo R., Mainardi F., and Vivoli A., Continuous-time random walk and parametric subordination in fractional diffusion, Chaos, Solitons & Fractals. (2007) 34, no. 1, 87–103, https://doi.org/10.1016/j.chaos.2007.01.052, MR2320430, ZBL1142.82363.
10.1016/j.chaos.2007.01.052
Web of Science® Google Scholar
4 Meerschaert M. M., Benson D. A., Scheffler H.-P., and Baeumer B., Stochastic solution of space-time fractional diffusion equations, Physical Review E. (2002) 65, no. 4, 4, 041103, https://doi.org/10.1103/PhysRevE.65.041103, MR1917983.
10.1103/PhysRevE.65.041103
CAS PubMed Web of Science® Google Scholar
5 Metzler R. and Klafter J., The random walk′s guide to anomalous diffusion: a fractional dynamics approach, Physics Reports A. (2000) 339, no. 1, 1–77, https://doi.org/10.1016/S0370-1573(00)00070-3, MR1809268, ZBL0984.82032.
10.1016/S0370-1573(00)00070-3
CAS Web of Science® Google Scholar
6 Scalas E., Gorenflo R., and Mainardi F., Uncoupled continuous-time random walks: solution and limiting behavior of the master equation, Physical Review E. (2004) 69, no. 1, 8, 011107, https://doi.org/10.1103/PhysRevE.69.011107, MR2097999.
10.1103/PhysRevE.69.011107
CAS PubMed Web of Science® Google Scholar
7 Dubkov A. A., Spagnolo B., and Uchaikin V. V., Lévy flight superdiffusion: an introduction, International Journal of Bifurcation and Chaos. (2008) 18, no. 9, 2649–2672, https://doi.org/10.1142/S0218127408021877, MR2479323, ZBL1157.82300.
10.1142/S0218127408021877
Web of Science® Google Scholar
8 Schneider W. R., S. Albeverio, G. Casati, U. Cattaneo, D. Merlini, and R. Moresi, Grey noise, Stochastic Processes, Physics and Geometry (Ascona and Locarno, 1988), 1990, World Scientific, Teaneck, NJ, USA, 676–681, MR1124240.
Google Scholar
9 Schneider W. R., S. Albeverio, J. E. Fenstad, H. Holden, and T. Lindstrøm, Grey noise, Ideas and Methods in Mathematical Analysis, Stochastics, and Applications (Oslo, 1988), 1992, Cambridge University Press, Cambridge, UK, 261–282, MR1190506, ZBL0761.60036.
Google Scholar
10 Chechkin A. V., [email protected], Gorenflo R., and [email protected], Sokolov I. M., [email protected], Retarding subdiffusion and accelerating superdiffusion governed by distributed-order fractional diffusion equations, Physical Review E. (2002) 66, no. 4, 7, 046129, 2-s2.0-6744272549, https://doi.org/10.1103/PhysRevE.66.046129.
10.1103/PhysRevE.66.046129
CAS PubMed Web of Science® Google Scholar
11 Chechkin A. V., Gorenflo R., Sokolov I. M., and Gonchar V. Yu., Distributed order time fractional diffusion equation, Fractional Calculus & Applied Analysis. (2003) 6, no. 3, 259–279, MR2035651, ZBL1089.60046.
Google Scholar
12 Chechkin A. V., Gonchar V. Yu., Gorenflo R., Korabel N., and Sokolov I. M., Generalized fractional diffusion equations for accelerating subdiffusion and truncated Lévy flights, Physical Review E. (2008) 78, no. 2, 13, 021111, https://doi.org/10.1103/PhysRevE.78.021111, MR2496818.
10.1103/PhysRevE.78.021111
CAS Web of Science® Google Scholar
13 Gorenflo R., Mainardi F., Moretti D., and Paradisi P., Time fractional diffusion: a discrete random walk approach, Nonlinear Dynamics. (2002) 29, no. 1–4, 129–143, https://doi.org/10.1023/A:1016547232119, MR1926470, ZBL1009.82016.
10.1023/A:1016547232119
Web of Science® Google Scholar
14 Gorenflo R., Mainardi F., [email protected], Moretti D., Pagnini G., and Paradisi P., Discrete random walk models for space-time fractional diffusion, Chemical Physics. (2002) 284, no. 1-2, 521–541, 2-s2.0-0032049827, https://doi.org/10.1016/S0301-0104(02)00714-0.
10.1016/S0301-0104(02)00714-0
CAS Web of Science® Google Scholar
15 Liu F., Shen S., Anh V., and Turner I., Analysis of a discrete non-Markovian random walk approximation for the time fractional diffusion equation, The ANZIAM Journal. (2005) 46, C488–C504, MR2182183.
10.21914/anziamj.v46i0.973
Google Scholar
16 Liu F., Zhuang P., Anh V., Turner I., and Burrage K., Stability and convergence of the difference methods for the space-time fractional advection-diffusion equation, Applied Mathematics and Computation. (2007) 191, no. 1, 12–20, https://doi.org/10.1016/j.amc.2006.08.162, MR2385498.
10.1016/j.amc.2006.08.162
Web of Science® Google Scholar
17 Zhang Y., Benson D. A., Meerschaert M. M., and Scheffler H.-P., On using random walks to solve the space-fractional advection-dispersion equations, Journal of Statistical Physics. (2006) 123, no. 1, 89–110, https://doi.org/10.1007/s10955-006-9042-x, MR2225237, ZBL1092.82038.
10.1007/s10955-006-9042-x
Web of Science® Google Scholar
18 Zhuang P. and Liu F., Implicit difference approximation for the time fractional diffusion equation, Journal of Applied Mathematics & Computing. (2006) 22, no. 3, 87–99, https://doi.org/10.1007/BF02832039, MR2323899, ZBL1140.65094.
10.1007/BF02832039
Google Scholar
19 Mura A., Non-Markovian stochastic processes and their applications: from anomalous diffusion to time series analysis, Ph.D. thesis, March 2008, Department of Physics, University of Bologna, Supervisor Prof. F. Mainardi, http://www.fracalmo.org/mura/.
Google Scholar
20 Mura A. and Mainardi F., A class of self-similar stochastic processes with stationary increments to model anomalous diffusion in physics, Integral Transforms and Special Functions. (2009) 20, no. 3-4, 185–198, https://doi.org/10.1080/10652460802567517, MR2501791, ZBL1173.26005.
10.1080/10652460802567517
Web of Science® Google Scholar
21 Mura A. and Pagnini G., Characterizations and simulations of a class of stochastic processes to model anomalous diffusion, Journal of Physics A. (2008) 41, no. 28, 22, 285003, https://doi.org/10.1088/1751-8113/41/28/285003, MR2430462, ZBL1143.82028.
10.1088/1751-8113/41/28/285003
Google Scholar
22 Mura A., [email protected], Taqqu M. S., and Mainardi F., Non-Markovian diffusion equations and processes: analysis and simulations, Physica A. (2008) 387, no. 21, 5033–5064, 2-s2.0-36149013316, https://doi.org/10.1016/j.physa.2008.04.035.
10.1016/j.physa.2008.04.035
Web of Science® Google Scholar
23 Caputo M., Linear models of dissipation whose Q is almost frequency independent—part II, Geophysical Journal of the Royal Astronomical Society. (1967) 13, 529–539.
10.1111/j.1365-246X.1967.tb02303.x
Web of Science® Google Scholar
24 Caputo M., Elasticity and Dissipation, 1969, Zanichelli, Bologna, Italy.
Google Scholar
25 Gorenflo R. and Mainardi F., A. Carpinteri and F. Mainardi, Fractional calculus: integral and differential equations of fractional order, Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996), 1997, 378, Springer, Vienna, Austria, 223–276, CISM Courses and Lectures, MR1611585.
10.1007/978-3-7091-2664-6_5
Google Scholar
26 Mainardi F. and Gorenflo R., Time-fractional derivatives in relaxation processes: a tutorial survey, Fractional Calculus & Applied Analysis. (2007) 10, no. 3, 269–308, MR2382782, ZBL1157.26304.
Google Scholar
27 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, MR1658022, ZBL0924.34008.
Web of Science® Google Scholar
28 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, 204, Elsevier Science B.V., Amsterdam, The Netherlands, North-Holland Mathematics Studies, MR2218073, ZBL1092.45003.
10.1016/S0304-0208(06)80001-0
Google Scholar
29 Wright E. M., On the coefficients of power series having exponential singularities, Journal of the London Mathematical Society. (1933) 8, 71–79.
10.1112/jlms/s1-8.1.71
PubMed Google Scholar
30 Wright E. M., The asymptotic expansion of the generalized Bessel function, Proceedings of the London Mathematical Society. (1935) 38, 257–270.
10.1112/plms/s2-38.1.257
PubMed Google Scholar
31 Wright E. M., The asymptotic expansion of the generalized hypergeometric function, Journal of the London Mathematical Society. (1935) 10, 287–293.
Google Scholar
32 Wright E. M., The generalized Bessel function of order greater than one, The Quarterly Journal of Mathematics. (1940) 11, 36–48, MR0003875, ZBL0023.14101.
10.1093/qmath/os-11.1.36
Google Scholar
33 Erdélyi A., Magnus W., Oberhettinger F., and Tricomi F. G., Higher Transcendental Functions, 1954, 3, no. chapter 18, McGraw-Hill, New-York, NY, USA.
Google Scholar
34 Gorenflo R., Luchko Yu., and Mainardi F., Analytical properties and applications of the Wright function, Fractional Calculus & Applied Analysis. (1999) 2, no. 4, 383–414, MR1752379, ZBL1027.33006.
Google Scholar
35 Gorenflo R., Luchko Yu., and Mainardi F., Wright functions as scale-invariant solutions of the diffusion-wave equation, Journal of Computational and Applied Mathematics. (2000) 118, no. 1-2, 175–191, https://doi.org/10.1016/S0377-0427(00)00288-0, MR1765948, ZBL0973.35012.
10.1016/S0377-0427(00)00288-0
Web of Science® Google Scholar
36 Kilbas A. A., Saigo M., and Trujillo J. J., On the generalized Wright function, Fractional Calculus & Applied Analysis. (2002) 5, no. 4, 437–460, MR1967844, ZBL1027.33015.
Google Scholar
37 Kiryakova V., Generalized Fractional Calculus and Applications, 1994, 301, Longman Scientific & Technical, Harlow, UK, Pitman Research Notes in Mathematics Series, MR1265940, ZBL0882.26003.
Google Scholar
38 Mainardi F., A. Carpinteri and F. Mainardi, Fractional calculus: some basic problems in continuum and statistical mechanics, Fractals and Fractional Calculus in Continuum Mechanics (Udine, 1996), 1997, 378, Springer, Vienna, Austria, 291–348, CISM Courses and Lectures, MR1611587, ZBL0917.73004.
10.1007/978-3-7091-2664-6_7
Google Scholar
39 Stanković B., On the function of E. M. Wright, Publications de l′Institut Mathèmatique. (1970) 10 (24), 113–124, MR0280762, ZBL0204.08404.
Google Scholar
40 Wong R. and Zhao Y.-Q., Smoothing of Stokes′s discontinuity for the generalized Bessel function, Proceedings of the Royal Society A. (1999) 455, no. 1984, 1381–1400, https://doi.org/10.1098/rspa.1999.0365, MR1701756, ZBL0974.41021.
10.1098/rspa.1999.0365
Google Scholar
41 Wong R. and Zhao Y.-Q., Smoothing of Stokes′s discontinuity for the generalized Bessel function. II, Proceedings of the Royal Society A. (1999) 455, no. 1988, 3065–3084, https://doi.org/10.1098/rspa.1999.0440, MR1807056, ZBL0974.41021.
10.1098/rspa.1999.0440
Google Scholar
42 Mainardi F., S. Rionero and T. Ruggeri, On the initial value problem for the fractional diffusion-wave equation, Waves and Stability in Continuous Media (Bologna, 1993), 1994, 23, World Scientific, River Edge, NJ, USA, 246–251, Series on Advances in Mathematics for Applied Sciences, MR1320083.
Google Scholar
43 Mainardi F. and Tomirotti M., P. Rusev, I. Dimovski, and V. Kiryakova, On a special function arising in the time fractional diffusion-wave equation, Transform Methods and Special Functions, Sofia 1994, 1995, Science Culture Technology, Singapore, 171–183.
Google Scholar
44 Bender C. M. and Orszag S. A., Advanced Mathematical Methods for Scientists and Engineers, 1987, McGraw-Hill, Singapore.
Google Scholar
45 Hanyga A., Multi-dimensional solutions of space-time-fractional diffusion equations, Proceedings of the Royal Society A. (2002) 458, no. 2018, 429–450, https://doi.org/10.1098/rspa.2001.0893, MR1889936, ZBL0999.60035.
10.1098/rspa.2001.0893
Google Scholar
46 Balescu R., V-Langevin equations, continuous time random walks and fractional diffusion, Chaos, Solitons & Fractals. (2007) 34, no. 1, 62–80, https://doi.org/10.1016/j.chaos.2007.01.050, MR2320428, ZBL1142.82356.
10.1016/j.chaos.2007.01.050
Web of Science® Google Scholar
47 Germano G., Politi M., Scalas E., and Schilling R. L., Stochastic calculus for uncoupled continuous-time random walks, Physical Review E. (2009) 79, no. 6, 12, 066102, https://doi.org/10.1103/PhysRevE.79.066102, MR2551283.
10.1103/PhysRevE.79.066102
Web of Science® Google Scholar
48 Kiryakova V., [email protected], The multi-index Mittag-Leffler functions as an important class of special functions of fractional calculus, Computers and Mathematics with Applications. In press2-s2.0-70049116485, https://doi.org/10.1016/j.camwa.2009.08.025.
10.1016/j.camwa.2009.08.025
Google Scholar
49 Kiryakova V., [email protected], The special functions of fractional calculus as generalized fractional calculus operators of some basic functions, Computers and Mathematics with Applications. (2010) 59, no. 3, 1128–1141, 2-s2.0-67649297800, https://doi.org/10.1016/j.camwa.2009.05.014.
10.1016/j.camwa.2009.05.014
Web of Science® Google Scholar
50 Mainardi F., Gorenflo R., and Vivoli A., Renewal processes of Mittag-Leffler and Wright type, Fractional Calculus & Applied Analysis. (2005) 8, no. 1, 7–38, MR2179226, ZBL1126.60070.
Google Scholar
51 Mainardi F. and Pagnini G., The Wright functions as solutions of the time-fractional diffusion equation, Applied Mathematics and Computation. (2003) 141, no. 1, 51–62, https://doi.org/10.1016/S0096-3003(02)00320-X, MR1984227, ZBL1053.35008.
10.1016/S0096-3003(02)00320-X
Web of Science® Google Scholar
52 Mainardi F., The fundamental solutions for the fractional diffusion-wave equation, Applied Mathematics Letters. (1996) 9, no. 6, 23–28, https://doi.org/10.1016/0893-9659(96)00089-4, MR1419811, ZBL0879.35036.
10.1016/0893-9659(96)00089-4
Web of Science® Google Scholar
53 Mainardi F., Luchko Yu., and Pagnini G., The fundamental solution of the space-time fractional diffusion equation, Fractional Calculus & Applied Analysis. (2001) 4, no. 2, 153–192, MR1829592, ZBL1054.35156.
Google Scholar
54 Feller W., An Introduction to Probability Theory and Its Applications. Vol. II, 1966, 1st edition, John Wiley & Sons, New York, NY, USA, MR0210154, ZBL0138.10207.
Google Scholar
55 Feller W., An Introduction to Probability Theory and Its Applications. Vol. II, 1971, 2nd edition, John Wiley & Sons, New York, NY, USA, MR0270403, ZBL0219.60003.
Google Scholar
56 Humbert P., Nouvelles correspondances symboliques, Bulletin des Sciences Mathématiques. (1945) 69, 121–129, MR0015564, ZBL0060.25112.
Google Scholar
57 Pollard H., The representation of as a Laplace integral, Bulletin of the American Mathematical Society. (1946) 52, 908–910, MR0018286, https://doi.org/10.1090/S0002-9904-1946-08672-3, ZBL0060.25007.
10.1090/S0002-9904-1946-08672-3
Web of Science® Google Scholar
58 Mikusiński J., On the function whose Laplace-transform is , Studia Mathematica. (1959) 18, 191–198, MR0108694, ZBL0087.10501.
10.4064/sm-18-2-191-198
Google Scholar
59 Buchen P. W. and Mainardi F., Asymptotic expansions for transient viscoelastic waves, Journal de Mécanique. (1975) 14, no. 4, 597–608, 2-s2.0-0016628745.
Google Scholar
60 Mainardi F. and Gorenflo R., On Mittag-Leffler-type functions in fractional evolution processes, Journal of Computational and Applied Mathematics. (2000) 118, no. 1-2, 283–299, https://doi.org/10.1016/S0377-0427(00)00294-6, MR1765955, ZBL0970.45005.
10.1016/S0377-0427(00)00294-6
Web of Science® Google Scholar
61 Achar B. N. N., Hanneken J. W., and Clarke T., Damping characteristics of a fractional oscillator, Physica A. (2004) 339, no. 3-4, 311–319, https://doi.org/10.1016/j.physa.2004.03.030, MR2091376.
10.1016/j.physa.2004.03.030
Web of Science® Google Scholar
62 Mainardi F., Fractional Calculus and Waves in Linear Viscoelasticity, 2010, Imperial College Press, London, UK.
10.1142/p614
Google Scholar
63 Freed A., Diethelm K., and Luchko Yu., Fractional-order viscoelasticity (FOV): constitutive development using the fractional calculus, First Annual Report, 2002, no. NASA/TM-2002-211914, Gleen Research Center.
Google Scholar
64 Gorenflo R., Loutchko J., and Luchko Yu., Computation of the Mittag-Leffler function E_α,β(z) and its derivative, Fractional Calculus & Applied Analysis. (2002) 5, no. 4, 491–518, MR1967847, ZBL1027.33016.
Google Scholar
65 Podlubny I., Mittag-Leffler function, The MATLAB routine, http://www.mathworks.com/matlabcentral/fileexchange.
Google Scholar
66 Seybold H. J. and Hilfer R., Numerical results for the generalized Mittag-Leffler function, Fractional Calculus & Applied Analysis. (2005) 8, no. 2, 127–139, MR2179658, ZBL1123.33018.
Google Scholar
67 Doetsch G., Introduction to the Theory and Application of the Laplace Transformation, 1974, Springer, New York, NY, USA, MR0344810.
10.1007/978-3-642-65690-3
Google Scholar
68 Mainardi F., Fractional relaxation-oscillation and fractional diffusion-wave phenomena, Chaos, Solitons & Fractals. (1996) 7, no. 9, 1461–1477, https://doi.org/10.1016/0960-0779(95)00125-5, MR1409912, ZBL1080.26505.
10.1016/0960-0779(95)00125-5
Web of Science® Google Scholar
69 Mainardi F. and [email protected], Tomirotti M., Seismic pulse propagation with constant Q and stable probability distributions, Annali di Geofisica. (1997) 40, no. 5, 1311–1328, 2-s2.0-0000916799.
Google Scholar
70 Luchko Yu., Algorithms for evaluation of the Wright function for the real arguments′ values, Fractional Calculus & Applied Analysis. (2008) 11, no. 1, 57–75, MR2379273.
Google Scholar
71 Mainardi F., Pagnini G., and Gorenflo R., Mellin transform and subordination laws in fractional diffusion processes, Fractional Calculus & Applied Analysis. (2003) 6, no. 4, 441–459, MR2044309, ZBL1083.60032.
Google Scholar
72 Sokolov I. M. and Klafter J., From diffusion to anomalous diffusion: a century after Einstein′s Brownian motion, Chaos. (2005) 15, no. 2, 7, 026103, https://doi.org/10.1063/1.1860472, MR2150232, ZBL1080.82022.
10.1063/1.1860472
CAS PubMed Web of Science® Google Scholar
73 Mainardi F., Pagnini G., and Gorenflo R., Some aspects of fractional diffusion equations of single and distributed order, Applied Mathematics and Computation. (2007) 187, no. 1, 295–305, https://doi.org/10.1016/j.amc.2006.08.126, MR2323582, ZBL1122.26004.
10.1016/j.amc.2006.08.126
Web of Science® Google Scholar
74 Saichev A. I. and Zaslavsky G. M., Fractional kinetic equations: solutions and applications, Chaos. (1997) 7, no. 4, 753–764, https://doi.org/10.1063/1.166272, MR1604710, ZBL0933.37029.
10.1063/1.166272
CAS PubMed Web of Science® Google Scholar
75 Schneider W. R. and Wyss W., Fractional diffusion and wave equations, Journal of Mathematical Physics. (1989) 30, no. 1, 134–144, https://doi.org/10.1063/1.528578, MR974464, ZBL0692.45004.
10.1063/1.528578
Web of Science® Google Scholar
76 Gel′fand I. M. and Shilov G. E., Generalized Functions, Volume I, 1964, Academic Press, New York, NY, USA.
Google Scholar
77 Gorenflo R. and Mainardi F., R. Klages, G. Radons, and I. M. Sokolov, Continuous time random walk, Mittag-Leffler waiting time and fractional diffusion: mathematical aspects, Anomalous Transport: Foundations and Applications, 2008, no. chapter 4, Wiley-VCH, Weinheim, Germany, 93–127.
10.1002/9783527622979.ch4
Google Scholar
78 Meerschaert M. M. and Scheffler H.-P., Limit theorems for continuous-time random walks with infinite mean waiting times, Journal of Applied Probability. (2004) 41, no. 3, 623–638, MR2074812, https://doi.org/10.1239/jap/1091543414, ZBL1065.60042.
10.1239/jap/1091543414
Web of Science® Google Scholar
79 Gorenflo R., Mittag-Leffler waiting time, power laws, rarefaction, continuous time random walk, diffusion limit, Workshop on Fractional Calculus and Statistical Distributions, November 2009, Pala Campus, Pala-Kerala, India, Centre for Mathematical Sciences.
Google Scholar

Citing Literature

All articles

The M-Wright Function in Time-Fractional Diffusion Processes: A Tutorial Survey

Abstract

1. Introduction

2. Notions and Notations

2.1. Integral Transforms Pairs

2.2. Essentials of Fractional Calculus with Support in ℝ⁺

3. The Functions of the Wright Type

3.1. The General Wright Function

3.2. The Auxiliary Functions of the Wright Type

3.3. Special Cases

4. Properties and Plots of the Auxiliary Wright Functions in Real Domain

4.1. Exponential Laplace Transforms

4.2. Asymptotic Representation for Large Argument

4.3. Absolute Moments

4.4. The Laplace Transform of the M-Wright Function

4.5. The Fourier Transform of the Symmetric M-Wright Function

4.6. The Mellin Transform of the M-Wright Function

4.7. Plots of the Symmetric M-Wright Function

4.8. The 𝕄-Wright Function in Two Variables

5. Fractional Diffusion Equations

5.1. The Standard Diffusion Equation

5.2. The Stretched-Time Standard Diffusion Equation

5.3. The Time-Fractional Diffusion Equation

5.4. The Stretched Time-Fractional Diffusion Equation

6. Fractional Diffusion Processes with Stationary Increments

7. Concluding Discussion

Acknowledgments

Appendices

A. The Fundamental Solution of the Time-Fractional Diffusion Equation

B. The Fundamental Solution of the Time-Fractional Drift Equation

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The M-Wright Function in Time-Fractional Diffusion Processes: A Tutorial Survey

Abstract

1. Introduction

2. Notions and Notations

2.1. Integral Transforms Pairs

2.2. Essentials of Fractional Calculus with Support in ℝ+

3. The Functions of the Wright Type

3.1. The General Wright Function

3.2. The Auxiliary Functions of the Wright Type

3.3. Special Cases

4. Properties and Plots of the Auxiliary Wright Functions in Real Domain

4.1. Exponential Laplace Transforms

4.2. Asymptotic Representation for Large Argument

4.3. Absolute Moments

4.4. The Laplace Transform of the M-Wright Function

4.5. The Fourier Transform of the Symmetric M-Wright Function

4.6. The Mellin Transform of the M-Wright Function

4.7. Plots of the Symmetric M-Wright Function

4.8. The 𝕄-Wright Function in Two Variables

5. Fractional Diffusion Equations

5.1. The Standard Diffusion Equation

5.2. The Stretched-Time Standard Diffusion Equation

5.3. The Time-Fractional Diffusion Equation

5.4. The Stretched Time-Fractional Diffusion Equation

6. Fractional Diffusion Processes with Stationary Increments

7. Concluding Discussion

Acknowledgments

Appendices

A. The Fundamental Solution of the Time-Fractional Diffusion Equation

B. The Fundamental Solution of the Time-Fractional Drift Equation

References

Citing Literature

Figures

References

Related

Information

2.2. Essentials of Fractional Calculus with Support in ℝ⁺