If complexity is your problem, learning classifier systems (LCSs) may offer a solution. These rule-based, multifaceted, machine learning algorithms originated and have evolved in the cradle of evolutionary biology and artificial intelligence. The LCS concept has inspired a multitude of implementations adapted to manage the different problem domains to which it has been applied (e.g., autonomous robotics, classification, knowledge discovery, and modeling). One field that is taking increasing notice of LCS is epidemiology, where there is a growing demand for powerful tools to facilitate etiological discovery. Unfortunately, implementation optimization is nontrivial, and a cohesive encapsulation of implementation alternatives seems to be lacking. This paper aims to provide an accessible foundation for researchers of different backgrounds interested in selecting or developing their own LCS. Included is a simple yet thorough introduction, a historical review, and a roadmap of algorithmic components, emphasizing differences in alternative LCS implementations.

1. Introduction

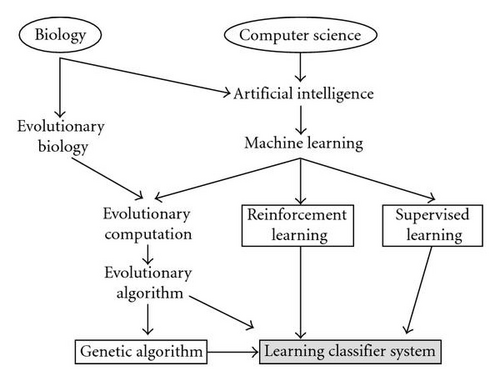
As our understanding of the world advances, the paradigm of a universe reigned by linear models, and simple “cause and effect” etiologies becomes staggeringly insufficient. Our world and the innumerable systems that it encompasses are each composed of interconnected parts that as a whole exhibit one or more properties not obvious from the properties of the individual parts. These “complex systems” feature a large number of interacting components, whose collective activity is nonlinear. Complex systems become “adaptive” when they possess the capacity to change and learn from experience. Immune systems, central nervous systems, stock markets, ecosystems, weather, and traffic are all examples of complex adaptive systems (CASs). In the book “Hidden Order,” John Holland specifically gives the example of New York City, as a system that exists in a steady state of operation, made up of “buyers, sellers, administrations, streets, bridges, and buildings [that] are always changing. Like the standing wave in front of a rock in a fast-moving stream, a city is a pattern in time.” Holland conceptually outlines the generalized problem domain of a CAS and characterizes how this type of system might be represented by rule-based “agents” [1]. The term “agent” is used to generally refer to a single component of a given system. Examples might include antibodies in an immune system, or water molecules in a weather system. Overall, CASs may be viewed as a group of interacting agents, where each agent′s behavior can be represented by a collection of simple rules. Rules are typically represented in the form of “IF condition THEN action”. In the immune system, antibody “agents” possess hyper-variable regions in their protein structure, which allows them to bind to specific targets known as antigens. In this way the immune system has a way to identify and neutralize foreign objects such as bacteria and viruses. Using this same example, the behavior of a specific antibody might be represented by rules such as “IF the antigen-binding site fits the antigen THEN bind to the antigen”, or “IF the antigen-binding site does not fit the antigen THEN do not bind to the antigen”. Rules such as these use information from the system′s environment to make decisions. Knowing the problem domain and having a basic framework for representing that domain, we can begin to describe the LCS algorithm. At the heart of this algorithm is the idea that, when dealing with complex systems, seeking a single best-fit model is less desirable than evolving a population of rules which collectively model that system. LCSs represent the merger of different fields of research encapsulated within a single algorithm. Figure 1 illustrates the field hierarchy that founds the LCS algorithmic concept. Now that the basic LCS concept and its origin have been introduced, the remaining sections are organized as follows: Section 2 summarizes the founding components of the algorithm, Section 3 discusses the major mechanisms, Section 4 provides an algorithmic walk through of a very simple LCS, Section 5 provides a historical review, Section 6 discusses general problem domains to which LCS has been applied, Section 7 identifies biological applications of the LCS algorithm, Section 8 briefly introduces some general optimization theory, Section 9 outlines a roadmap of algorithmic components, Section 10 gives some overall perspective on future directions for the field, and Section 11 identifies some helpful resources.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Field tree—foundations of the LCS community.

2. A General LCS

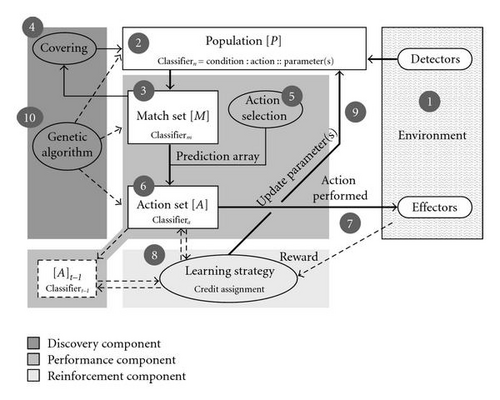
Let us begin with a conceptual tour of LCS anatomy. As previously mentioned, the core of an LCS is a set of rules (called the population of classifiers). The desired outcome of running the LCS algorithm is for those classifiers to collectively model an intelligent decision maker. To obtain that end, “LCSs employ two biological metaphors; evolution and learning… [where] learning guides the evolutionary component to move toward a better set of rules.” [2] These concepts are respectively embodied by two mechanisms: the genetic algorithm, and a learning mechanism appropriate for the given problem (see Sections 3.1 and 3.2 resp.). Both mechanisms rely on what is referred to as the “environment” of the system. Within the context of LCS literature, the environment is simply the source of input data for the LCS algorithm. The information being passed from the environment is limited only by the scope of the problem being examined. Consider the scenario of a robot being asked to navigate a maze environment. Here, the input data may be in the form of sensory information roughly describing the robot′s physical environment [3]. Alternatively, for a classification problem such as medical diagnosis, the environment is a training set of preclassified subjects (i.e., cases and controls) described by multiple attributes (e.g., genetic polymorphisms). By interacting with the environment, LCSs receive feedback in the form of numerical reward which drives the learning process. While many different implementations of LCS algorithms exist, Holmes et al. [4] outline four practically universal components: (1) a finite population of classifiers that represents the current knowledge of the system, (2) a performance component, which regulates interaction between the environment and classifier population, (3) a reinforcement component (also called credit assignment component [5]), which distributes the reward received from the environment to the classifiers, and (4) a discovery component which uses different operators to discover better rules and improve existing ones. Together, these components represent a basic framework upon which a number of novel alterations to the LCS algorithm have been built. Figure 2 illustrates how specific mechanisms of LCS (detailed in Section 9) interact in the context of these major components.

3. The Driving Mechanisms

While the above four components represent an algorithmic framework, two primary mechanisms are responsible for driving the system. These include discovery, generally by way of the genetic algorithm, and learning. Both mechanisms have generated respective fields of study, but it is in the context of LCS that we wish to understand their function and purpose.

3.1. Discovery—The Genetic Algorithm

Discovery refers to “rule discovery” or the introduction of rules that do not currently exist in the population. Ideally, new rules will be better at getting payoff (i.e., making good decisions) than existing ones. From the start, this task has almost always been achieved through the use of a genetic algorithm (GA). The GA is a computational search technique which manipulates (evolves) a population of individuals (rules) each representing a potential solution (or piece of a solution) to a given problem. The GA, as a major component of the first conceptualized LCS [6], has largely surpassed LCS in terms of celebrity and common usage. GAs [7, 8] are founded on ideas borrowed from nature. Inspired from the neo-Darwinist theory of natural selection, the evolution of rules is modeled after the evolution of organisms using four biological analogies: (1) a code is used to represent the genotype/genome (condition), (2) a solution (or phenotype) representation is associated with that genome (action), (3) a phenotype selection process (survival of the fittest), where the fittest organism (rule) has a greater chance of reproducing and passing its “genetic” information on to the next generation, and (4) genetic operators are utilized to allow simple transformations of the genome in search of fitter organisms (rules) [9, 10]. Variation in a genome (rule) is typically generated by two genetic operators: mutation and crossover (recombination). Crossover operators create new genotypes by recombining subparts of the genotypes of two or more individuals (rules). Mutation operators randomly modify an element in the genotype of an individual (rule). The selection pressure which drives “better” organisms (rules) to reproduce more often is dependent on the fitness function. The fitness function quantifies the optimality of a given rule, allowing that rule to be ranked against all other rules in the population. In a simple classification problem, one might use classification accuracy as a metric of fitness. Running a genetic algorithm requires looping through a series of steps for some number of iterations (generations). Initially, the user must predefine a number of parameters such as the population size (N) and the number of generations, based on the user′s needs. Additionally the GA needs to be initialized with a population of rules which can be generated randomly to broadly cover the range of possible solutions (the search space). The following steps will guide the reader through a single iteration of a simple genetic algorithm.

(1)
Evaluate the fitness of all rules in the current population.
(2)
Select “parent” rules from the population (with probability proportional to fitness).
(3)
Crossover and/or mutate “parent” rules to form “offspring” rules.
(4)
Add “offspring” rules to the next generation.
(5)
Remove enough rules from the next generation (with probability of being removed inversely proportional to fitness) to restore the number of rules to N.

As with LCSs, there are a variety of GA implementations which may vary the details underlying the steps described above (see Section 9.5). GA research constitutes its own field which goes beyond the scope of this paper. For a more detailed introduction to GAs we refer readers to Goldberg [8, 11].

3.2. Learning

In the context of artificial intelligence, learning can be defined as, “the improvement of performance in some environment through the acquisition of knowledge resulting from experience in that environment” [12]. This notion of learning via reinforcement (also referred to as credit assignment [3]) is an essential mechanism of the LCS architecture. Often the terms learning, reinforcement, and credit assignment are used interchangeably within the literature. In addition to a condition and action, each classifier in the LCS population has one or more parameter values associated with it (e.g., fitness). The iterative update of these parameter values drives the process of LCS reinforcement. More generally speaking, the update of parameters distributes any incoming reward (and/or punishment) to the classifiers that are accountable for it. This mechanism serves two purposes: (1) to identify classifiers that are useful in obtaining future rewards and (2) to encourage the discovery of better rules. Many of the existing LCS implementations utilize different learning strategies. One of the main reasons for this is that different problem domains demand different styles of learning. For example, learning can be categorized based on the manner in which information is received from this environment. Offline or “batch” learning implies that all training instances are presented simultaneously to the learner. The end result is a single rule set embodying a solution that does not change with respect to time. This type of learning is often characteristic of data mining problems. Alternatively, online or “incremental” learning implies that training instances are presented to the learner one at a time, the end result of which is a rule set which changes continuously with the addition of each additional observation [12–14]. This type of learning may have no prespecified endpoint, as the system solution may continually modify itself with respect to a continuous stream of input. Consider, for example, a robot which receives a continuous stream of data about the environment it is attempting to navigate. Over time it may need to adapt its movements to maneuver around obstacles it has not yet faced. Learning can also be distinguished by the type of feedback that is made available to the learner. In this context, two learning styles have been employed by LCSs; supervised learning and reinforcement learning, of which the latter is often considered to be synonymous with LCS. Supervised learning implies that for each training instance, the learner is supplied not only with the condition information, but also with the “correct” action. The goal here is to infer a solution that generalizes to unseen instances based on training examples that possess correct input/output pairs. Reinforcement learning (RL), on the other hand, is closer to unsupervised learning, in that the “correct” action of a training instance is not known. However, RL problems do provide feedback, indicating the “goodness” of an action decision with respect to some goal. In this way, learning is achieved through trial-and-error interactions with the environment where occasional immediate reward is used to generate a policy that maximizes long term reward (delayed reward). The term `policy′ is used to describe a state-action map which models the agent-environment interactions. For a detailed introduction to RL we refer readers to Sutton and Barto (1998) [15], Harmon (1996) [16], and Wyatt (2005) [17]. Specific LCS learning schemes will be discussed further in Section 9.4.

4. A Minimal Classifier System

The working LCS algorithm is a relatively complex assembly of interacting mechanisms operating in an iterative fashion. We complete our functional introduction to LCSs with an algorithmic walk through. For simplicity, we will explore what might be considered one of the most basic LCS implementations, a minimal classifier system (MCS) [18]. This system is heavily influenced by modern LCS architecture. For an earlier perspective on simple LCS architecture see Goldberg′s SCS [8]. MCS was developed by Larry Bull as a platform for advancing LCS theory. While it was not designed for real-world applications, MCS offers a convenient archetype upon which to better understand more complex implementations. Figure 3 outlines a single iteration of MCS. In this example the input data takes the form of a four-digit binary number, representing discrete observations detected from an instance in the environment. MCS learns iteratively, sampling one data instance at a time, learning from it, and then moving to the next. As usual, a population of classifiers represents the evolving solution to our given problem. Each of the (N) classifiers in the population are made up of a condition, an action, and an associated fitness parameter {F}. The condition is represented by a string of characters from the ternary alphabet 0,1, # where # acts as a wildcard such that the rule condition 00#1 matches both the input 0011 and the input 0001. The action is represented by a binary string where in this case only two actions are possible (0 or 1). The fitness parameter gives an indication of how good a given classifier is, which is important not only for action selection, but for application of the GA to evolve better and better classifiers. Before the algorithm is run, the population of classifiers is randomly initialized, and the fitness parameters are each set to some initial value f₀. Figure 3 depicts the MCS after having already been run for a number of iterations made evident by the diversity of fitness scores. With the receipt of input data, the population is scanned and any rule whose condition matches the input string at each position becomes a member of the current “match set” [M]. If none of the rules in the population match the input, a covering operator generates a rule with a matching condition and a random action [19]. The number of wildcards incorporated into the new rule condition is dependent on the rate (p_#) set by the user. With the addition of a new rule, an existing rule must be removed from the population to keep (N) constant. This is done using roulette wheel selection where the probability of a rule being selected for replacement is inversely proportional to its fitness, that is, 1/(F_j + 1) [20, 21]. Once the match set is established, an action is selected using a simple explore/exploit scheme [22]. This scheme alternates between randomly selecting an action found within [M] one round (explore), and selecting deterministically with a prediction array the next (exploit). The prediction array is a list of prediction values calculated for each action found in [M]. In MCS, the prediction value is the sum of fitness values found in the subset of [M] advocating the same action. The subset with the highest prediction value becomes the action set [A], and the corresponding action is performed in the environment. Learning begins with receipt of an immediate reward (payoff = P) from the environment in response to the performed action. MCS uses a simple form of RL that uses the Widrow-Hoff procedure (see Section 9.4.2) with a user defined learning rate of β. The following equation updates the fitness of each rule in the current [A]:

()

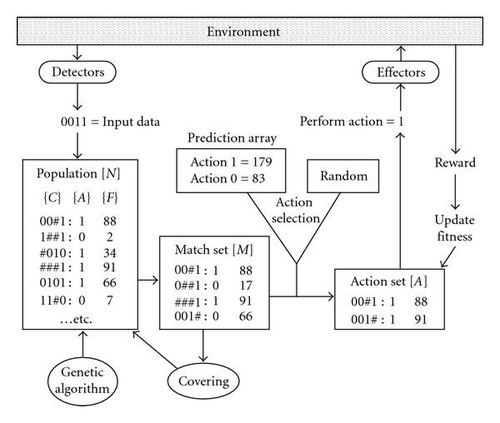
The final step in MCS is the activation of a GA that operates within the entire population (panmitic). Together the GA and the covering operator make up the discovery mechanism of MCS. The GA operates as previously described where on each “explore” iteration, there is a probability (g) of GA invocation. This probability is only applied to “explore” iterations where action selection is performed randomly. Parent rules are selected from the population using roulette wheel selection. Offspring are produced using a mutation rate of (μ) (with a wildcard rate of (p_#)) and a single point crossover rate of (χ). New rules having undergone mutation inherit their parent′s fitness values, while those that have undergone crossover inherit the average fitness of the parents. New rules replace old ones as previously described. MCS is iterated in this manner over a user defined number of generations.

5. Historical Perspective

The LCS concept, now three decades old, has inspired a wealth of research aimed at the development, comparison, and comprehension of different LCSs. The vast majority of this work is based on a handful of key papers [3, 19, 22–24] which can be credited with founding the major branches of LCS. These works have become the founding archetypes for an entire generation of LCS algorithms which seek to improve algorithmic performance when applied to different problem domains. As a result, many LCS algorithms are defined by an expansion, customization, or merger of one of the founding algorithms. Jumping into the literature, it is important to note that the naming convention used to refer to the LCS algorithm has undergone a number of changes since its infancy. John Holland, who formalized the original LCS concept [25] based around his more well-known invention, the Genetic Algorithm (GA) [6], referred to his proposal simply as a classifier system, abbreviated either as (CS), or (CFS) [26]. Since that time, LCSs have also been referred to as adaptive agents [1], cognitive systems [3], and genetics-based machine learning systems [2, 8]. On occasion they have quite generically been referred to as either production systems [6, 27] or genetic algorithms [28] which in fact describes only a part of the greater system. The now standard designation of a “learning classifier system” was not adopted until the late 80s [29] after Holland added a reinforcement component to the CS architecture [30, 31]. The rest of this section provides a synopsis of some of the most popular LCSs to have emerged, and the contributions they made to the field. This brief history is supplemented by Table 1 which chronologically identifies noted LCS algorithms/platforms and details some of the defining features of each. This table includes the LCS style (Michigan {M}, Pittsburgh {P}, Hybrid {H}, and Anticipatory {A}), the primary fitness basis, a summary of the learning style or credit assignment scheme, the manner in which rules are represented, the position in the algorithm at which the GA is invoked (panmitic [P], match set [M], action set [A], correct set [C], local neighborhood LN, and modified LN (MLN) and the problem domain(s)) on which the algorithm was designed and/or tested.

Table 1. A summary of noted LCS algorithms

System	Year	Author/cite	Style	Fitness	Learning/credit assignment	Rule rep.	GA	Problem
CS-1	1978	Holland [3]	M	Accuracy	Epochal	Ternary	[P]	Maze Navigation
LS-1	1980	Smith [23]	P	Accuracy	Implicit Critic	Ternary	[P]	Poker Decisions
CS-1 (based)	1982	Booker [42]	M	Strength	Bucket Brigade	Ternary	[M]	Environment Navigation
Animat CS	1985	Wilson [44]	M	Strength	Implicit Bucket Brigade	Ternary	[P]	Animat Navigation
LS-2	1985	Schaffer [56]	P	Accuracy	Implicit Critic	Ternary	[P]	Classification
Standard CS	1986	Holland [30]	M	Strength	Bucket Brigade	Ternary	[P]	Online Learning
BOOLE	1987	Wilson [43]	M	Strength	One-Step Payoff-Penalty	Ternary	[P]	Boolean Function Learning
ADAM	1987	Greene [57]	P	Accuracy	Custom	Ternary	[P]	Classification
RUDI	1988	Grefenstette [58]	H	Strength	Bucket-Brigade and Profit-Sharing Plan	Ternary	[P]	Generic Problem Solving
GOFER	1988	Booker [59]	M	Strength	Payoff-Sharing	Ternary	[M]	Environment Navigation
GOFER-1	1989	Booker [47]	M	Strength	Bucket-Brigade-like	Ternary	[M]	Multiplexer Function
SCS	1989	Goldberg [8]	M	Strength	AOC	Trit	[P]	Multiplexer Function
SAMUEL	1989–1997	Grefenstette [60–62]	H	Strength	Profit-Sharing Plan	Varied	[P]	Sequential Decision Tasks
NEWBOOLE	1990	Bonelli [46]	M	Strength	Symmetrical Payoff-Penalty	Ternary	[P]	Classification
CFCS2	1991	Riolo [55]	M	Strength/ Accuracy	Q-Learning-Like	Ternary	[P]	Maze Navigation
HCS	1991	Shu [63]	H	Strength	Custom	Ternary	[P]	Boolearn Function Learning
Fuzzy LCS	1991	Valenzuela-Rendon [48]	M	Strength	Custom Bucket-Brigade	Binary - Fuzzy Logic	[P]	Classification
ALECSYS	1991–1995	Dorigo [64, 65]	M	Strength	Bucket Brigade	Ternary	[P]	Robotics
GABIL	1991-1993	De Jong [66, 67]	P	Accuracy	Batch - Incremental	Binary - CNF	[P]	Classification
GIL	1991–1993	Janikow [68, 69]	P	Accuracy	Supervised Learning - Custom	Multi-valued logic (VL1)	[P]	Multiple Domains
GARGLE	1992	Greene [70]	P	Accuracy	Custom	Ternary	[P]	Classification
COGIN	1993	Greene [71]	M	Accuracy/ Entropy	Custom	Ternary	[P]	Classification, Model Induction
REGAL	1993	Giordana [72–74]	H	Accuracy	Custom	Binary - First Order Logic	[P]	Classification
ELF	1993–1996	Bonarini [75–77]	H	Strength	Q-Learning-Like	Binary - Fuzzy Logic	[P]	Robotics, Cart-Pole Problem
ZCS	1994	Wilson [19]	M	Strength	Implicit Bucket Brigade	Ternary	[P]	Environment Navigation
ZCSM	1994	Cliff [78]	M	Strength	Implicit Bucket Brigade - Memory	Ternary	[P]	Environment Navigation
XCS	1995	Wilson [22]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Mulitplexor Function and Environment Navigation
GA-Miner	1995–1996	Flockhart [79, 80]	H	Accuracy	Custom	Symbolic Functions	LN	Classification, Data Mining
BOOLE++	1996	Holmes [81]	M	Strength	Symmetrical Payoff-Penalty	Ternary	[P]	Epidemiologic Classification
EpiCS	1997	Holmes [82]	M	Strength	Symmetrical Payoff-Penalty	Ternary	[P]	Epidemiologic Classification
XCSM	1998	Lanzi [83, 84]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Environment Navigation
ZCCS	1998–1999	Tomlinson [85, 86]	H	Strength	Implicit Bucket Brigade	Ternary	[P]	Environment Navigation
ACS	1998–2000	Stolzmann [24, 87]	A	Strength/ Accuracy	Bucket-Brigade-like (reward or anticipation learning)	Ternary	—	Environment Navigation
iLCS	1999-2000	Browne [88, 89]	M	Strength/ Accuracy	Custom	Real-Value Alphabet	[P]	Industrial Applications - Hot Strip Mill
XCSMH	2000	Lanzi [90]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Non-Markov Environment Navigation
CXCS	2000	Tomlinson [91]	H	Accuracy	Q-Learning-Like	Ternary	[A]	Environment Navigation
XCSR	2000	Wilson [92]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Real-Valued Multiplexor Problems
ClaDia	2000	Walter [93]	M	Strength	Supervised Learning - Custom	Binary - Fuzzy Logic	[P]	Epidemiologic Classification
OCS	2000	Takadama [94]	O	Strength	Profit Sharing	Binary	[P]	Non-Markov Multiagent Environments
XCSI	2000-2001	Wilson [95, 96]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Integer-Valued Data Mining
MOLeCS	2000-2001	Bernado-Mansilla [97, 98]	M	Accuracy	Multiobjective Learning	Binary	[P]	Multiplexor Problem
YACS	2000–2002	Gerard [99, 100]	A	Accuracy	Latent Learning	Tokens	—	Non-Markov Environment Navigation
SBXCS	2001-2002	Kovacs [101, 102]	M	Strength	Q-Learning-Like	Ternary	[A]	Multiplexor Function
ACS2	2001-2002	Butz [103, 104]	A	Accuracy	Q-Learning-Like	Ternary	—	Environment Navigation
ATNoSFERES	2001–2007	Landau and Picault [105–109]	P	Accuracy	Custom	Graph-Based Binary-Tokens	[P]	Non-Markov Environment Navigation
GALE	2001-2002	Llora [110, 111]	P	Accuracy	Custom	Binary	LN	Classification, Data Mining
GALE2	2002	Llora [112]	P	Accuracy	Custom	Binary	MLN	Classification, Data Mining
XCSF	2002	Wilson [113]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Function Approximation
AXCS	2002	Tharakunnel [114]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Multi-step Problems Environmental Navigation
TCS	2002	Hurst [115]	M	Strength	Q-Learning-Like	Interval Predicates	[P]	Robotics
X-NCS	2002	Bull [116]	M	Accuracy	Q-Learning-Like	Neural Network	[A]	Multiple Domains
X-NFCS	2002	Bull [116]	M	Accuracy	Q-Learning-Like	Fuzzy - Neural Network	[A]	Function Approximation
UCS	2003	Bernado-Mansilla [117]	M	Accuracy	Supervised Learning - Custom	Ternary	[C]	Classification - Data Mining
XACS	2003	Butz [118]	A	Accuracy	Generalizing State Value Learner	Ternary	—	Blocks World Problem
XCSTS	2003	Butz [119]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Multiplexor Problem
MOLCS	2003	Llora [120]	P	Multiobjective	Custom	Ternary	[P]	Classification - LED Problem
YCS	2003	Bull [121]	M	Accuracy	Q-Learning-Like Widrow-Hoff	Ternary	[P]	Accuracy Theory - Multiplexor Problem
XCSQ	2003	Dixon [122]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Rule-set Reduction
YCSL	2004	Bull [123]	A	Accuracy	Latent Learning	Ternary	—	Environment Navigation
PICS	2004	Gaspar [124, 125]	P	Accuracy	Custom - Artificial Immune System	Ternary	[P]	Multiplexor Problem
NCS	2004	Hurst [126]	M	Strength	Q-Learning-Like	Neural Network	[P]	Robotics
MCS	2004	Bull [127]	M	Strength	Q-Learning-Like Widrow-Hoff	Ternary	[P]	Strength Theory - Multiplexor Problem
GAssist	2004–2007	Bacardit [128–131]	P	Accuracy	ILAS	ADI - Binary	[P]	Data Mining UCI Problems
MACS	2005	Gerard [132]	A	Accuracy	Latent Learning	Tokens	—	Non-Markov Environment Navigation
XCSFG	2005	Hamzeh [133]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Function Approximation
ATNoSFERES-II	2005	Landau [134]	P	Accuracy	Custom	Graph-Based Integer-Tokens	[P]	Non-Markov Environment Navigation
GCS	2005	Unold [135, 136]	M	Accuracy	Custom	Context-Free Grammar CNF	[P]	Learning Context-Free Languages
DXCS	2005	Dam [137–139]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Distributed Data Mining
LCSE	2005–2007	Gao [140–142]	M	Strength and Accuracy	Ensemble Learning	Interval Predicates	[A]	Data Mining UCI Problems
EpiXCS	2005–2007	Holmes [143–145]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Epidemiologic Data Mining
XCSFNN	2006	Loiacono [146]	M	Accuracy	Q-Learning-Like	Feedforward Multilayer Neural Network	[A]	Function Approximation
BCS	2006	Dam [147]	M	Bayesian	Supervised Learning - Custom	Ternary	[C]	Multiplexor Problem
BioHEL	2006	Bacardit [148, 149]	P	Accuracy	Custom	ADI - Binary	[P]	Larger Problems -Multiplexor, Protein Structure Prediction
XCSFGH	2006	Hamzeh [150]	M	Accuracy	Q-Learning-Like	Binary Polynomials	[A]	Function Approximation
XCSFGC	2007	Hamzeh [151]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Function Approximation
XCSCA	2007	Lanzi [152]	M	Accuracy	Supervised Learning - Custom	Interval Predicates	[M]	Environmental Navigation
LCSE	2007	Gao [142]	M	Accuracy	Q-Learning-Like	Interval Predicates	[A]	Medical Data Mining - Ensemble Learning
CB-HXCS	2007	Gershoff [153]	M	Accuracy	Q-Learning-Like	Ternary	[A]	Multiplexor Problem
MILCS	2007	Smith [154]	M	Accuracy	Supervised Learning - Custom	Neural Network	[C]	Multiplexor, Protein Structure
rGCS	2007	Cielecki [155]	M	Accuracy	Custom	Real-Valued Context-Free Grammar Based	[P]	Checkerboard Problem
Fuzzy XCS	2007	Casilas [156]	M	Accuracy	Q-Learning-Like	Binary - Fuzzy Logic	[A]	Single Step Reinforcement Problems
Fuzzy UCS	2007	Orriols-Puig [157]	M	Accuracy	Supervised Learning - Custom	Binary - Fuzzy Logic	[C]	Data Mining UCI Problems
NAX	2007	Llora [158]	P	Accuracy	Custom	Interval Predicates	[P]	Classification - Large Data Sets
NLCS	2008	Dam [2]	M	Accuracy	Supervised Learning - Custom	Neural Network	[C]	Classification

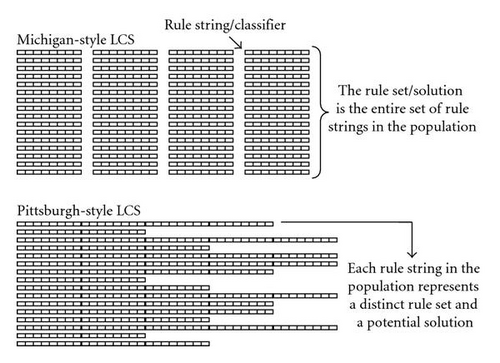
5.1. The Early Years

Holland′s earliest CS implementation, called Cognitive System One (CS-1) [3] was essentially the first learning classifier system, being the first to merge a credit assignment scheme with a GA in order to evolve a population of rules as a solution to a problem who′s environment only offered an infrequent payoff/reward. An immediate drawback to this and other early LCSs was the inherent complexity of the implementation and the lack of comprehension of the systems operation [8]. The CS-1 archetype, having been developed at the University of Michigan, would later inspire a whole generation of LCS implementations. These “Michigan-style” LCSs are characterized by a population of rules where the GA operates at the level of individual rules and the solution is represented by the entire rule population. Smith′s 1980 dissertation from the University of Pittsburgh [23] introduced LS-1, an alternative implementation that founded the fundamentally different “Pittsburgh-style” LCS. Also referred to as the “Pitt-approach”, the LS-1 archetype is characterized by a population of variable length rule-sets (each rule-set is a potential solution) where the GA typically operates at the level of an entire rule-set. An early advantage of the Pitt-approach came from its credit assignment scheme, where reward is assigned to entire rule-sets as opposed to individual rules. This allows Pitt-style systems such as LS-1 to circumvent the potential problem of having to share credit amongst individual rules. But, in having to evolve multiple rule sets simultaneously, Pitt-style systems suffer from heavy computational requirements. Additionally, because Pitt systems learn iteratively from sets of problem instances, they can only work offline, whereas Michigan systems are designed to work online, but can engage offline problems as well. Of the two styles, the Michigan approach has drawn the most attention as it can be applied to a broader range of problem domains and larger, more complex tasks. As such, it has largely become what many consider to be the standard LCS framework. All subsequent systems mentioned in this review are of Michigan-style unless explicitly stated otherwise. Following CS-1, Holland′s subsequent theoretical and experimental investigations [30–40] advocated the use of the bucket brigade credit assignment scheme (see Section 9.4.1). The bucket brigade algorithm (BBA), inspired by Samuel [41] and formalized by Holland [38] represents the first learning/credit assignment scheme to be widely adopted by the LCS community [20, 42, 43]. Early work by Booker on a CS-1 based system suggested a number of modifications including the idea to replace the panmictically acting GA with a niche-based one (i.e., the GA acts on [M] instead of [P]) [42]. The reason for this modification was to eliminate undesirable competition between unrelated classifiers, and to encourage more useful crossovers between classifiers of a common “environmental niche”. This in turn would help the classifier population retain diversity and encourage inclusion of problem subdomains in the solution. However, it should be noted that niching has the likely impact of making the GA more susceptible to local maxima, a disadvantage for problems with a solution best expressed as a single rule. In 1985, Stewart Wilson implemented an Animat CS [44] that utilized a simplified version of the bucket brigade, referred to later as an implicit bucket brigade [8]. Additionally, the Animat system introduced a number of concepts which persist in many LCSs today including covering (via a “create” operator), the formalization of an action set [A], an estimated time-to-payoff parameter incorporated into the learning scheme, and a general progression towards a simpler CS architecture [44, 45]. In 1986 Holland published what would become known as the standard CS for years to come [30]. This implementation incorporated a strength-based fitness parameter and BBA credit assignment as described in [38]. While still considered to be quite complex and susceptible to a number of problems [45], the design of this hallmark LCS is to this day a benchmark for all other implementations. The next year, Wilson introduced BOOLE, a CS developed specifically to address the problem of learning Boolean functions [43]. Characteristic of the Boolean problem, classifiers are immediately rewarded in response to performing actions. As a result BOOLE omits sequential aspects of the CS, such as the BBA which allows reward to be delayed over a number of time steps, instead relying on a simpler “one-step” CS. Bonelli et. al. [46] later extended BOOLE to a system called NEWBOOLE in order to improve the learning rate. NEWBOOLE introduced a “symmetrical payoff-penalty” (SPP) algorithm (reminiscent of supervised learning) which replaced [A] with a correct set [C], and not-correct set Not [C]. In 1989, Booker continued his work with GOFER-1 [47] adding a fitness function based on both payoff and nonpayoff information (e.g., strength and specificity), and further pursued the idea of a “niching” GA. Another novel system which spawned its own lineage of research is Valenzuela′s fuzzy LCS which combined fuzzy logic with the concept of a rule-based LCSs [48]. The fuzzy LCS represents one of the first systems to explore a rule representation beyond the simple ternary system. For an introduction to fuzzy LCS we refer readers to [49]. An early goal for LCSs was the capacity to learn and represent more complex problems using “internal models” as was originally envisioned by Holland [34, 38]. Work by Rick Riolo addressed the issues of forming “long action chains” and “default hierarchies” which had been identified as problematic for the BBA [29, 50, 51]. A long action chain refers to a series of rules which must sequentially activate before ultimately receiving some environmental payoff. They are challenging to evolve since “there are long delays before rewards are received, with many unrewarded steps between some stage setting actions and the ultimate action those actions lead to” [52]. Long chains are important for modeling behavior which require the execution of many actions before the receipt of a reward. A default hierarchy is a set of rules with increasing levels of specificity, where the action specified by more general rules is selected by “default” except in the case where overriding information is able to activate a more specific rule. “Holland has long argued that default hierarchies are an efficient, flexible, easy-to-discover way to categorize observations and structure models of the world” [52]. Reference [53] describes hierarchy formation in greater detail. Over the years a number of methods have been introduced in order to allow the structuring of internal models. Examples would include internal message lists, non-message-list memory mechanisms, “corporate” classifier systems, and enhanced rule syntax and semantics [52]. Internal message lists, part of the original CS-1 [3] exist as a means to handle all input and output communication between the system and the environment, as well as providing a makeshift memory for the system. While the message list component can facilitate complex internal structures, its presence accounts for much of the complexity in early LCS systems. The tradeoff between complexity and comprehensibility is a theme which has been revisited throughout the course of LCS research [45, 52, 54]. Another founding system is Riolo′s CFCS2 [55], which addressed the particularly difficult task of performing “latent learning” or “look-ahead planning” where “actions are based on predictions of future states of the world, using both current information and past experience as embodied in the agent′s internal models of the world” [52]. This work would later inspire its own branch of LCS research: anticipatory classifier systems (ACS) [24]. CFCS2 used “tags” to represent internal models, claiming a reduction in the learning time for general sequential decision tasks. Additionally, this system is one of the earliest to incorporate a Q-learning-like credit assignment technique (i.e., a nonbucket brigade temporal difference method). Q-learning-based credit assignment would later become a central component of the most popular LCS implementation to date.

5.2. The Revolution

From the late 80s until the mid-90s the interest generated by these early ideas began to diminish as researchers struggled with LCS′s inherent complexity and the failure of various systems to reliably obtain the behavior and performance envisioned by Holland. Two events have repeatedly been credited with the revitalization of the LCS community, namely the publication of the “Q-Learning” algorithm in the RL community, and the advent of a significantly simplified LCS architecture as found in the ZCS and XCS (see Table 1). The fields of RL and LCSs have evolved in parallel, each contributing to the other. RL has been an integral component of LCSs from the very beginning [3]. While the founding concepts of RL can be traced back to Samuel′s checker player [41], it was not until the 80s that RL became its own identifiable area of machine learning research [159]. Early RL techniques included Holland′s BBA [38] and Sutton′s temporal difference (TD) method [160] which was followed closely by Watkins′s Q-Learning method [161]. Over the years a handful of studies have confirmed the basic equivalence of these three methods, highlighting the distinct ties between the two fields. To summarize, the BBA was shown to be one kind of TD method [160], and the similarity between all three methods were noted by Watkins [161] and confirmed by Liepins, Dorigo, and Bersini [162, 163]. This similarity across fields paved the way for the incorporation of Q-learning-based techniques into LCSs. To date, Q-learning is the most well-understood and widely-used RL algorithm available. In 1994, Wilson′s pursuit of simplification culminated in the development of the “zeroth-level” classifier system (ZCS) [19], aimed at increasing the understandability and performance of an LCS. ZCS differed from the standard LCS framework in that it removed the rule-bidding and internal message list, both characteristic of the original BBA (see Section 9.3). Furthermore, ZCS was able to disregard a number of algorithmic components which had been appended to preceding systems in an effort to achieve acceptable performance using the original LCS framework (e.g., heuristics [44] and operators [164]). New to ZCS, was a novel credit assignment strategy that merged elements from the BBA and Q-Learning into the “QBB” strategy. This hybrid strategy represents the first attempt to bridge the gap between the major LCS credit assignment algorithm (i.e., the BBA) and other algorithms from the field of RL. With ZCS, Wilson was able to achieve similar performance to earlier, more complex implementations demonstrating that Holland′s ideas could work even in a very simple framework. However, ZCS still exhibited unsatisfactory performance, attributed to the proliferation of over-general classifiers. The following year, Wilson introduced an eXtended Classifier System (XCS) [22] noted for being able to reach optimal performance while evolving accurate and maximally general classifiers. Retaining much of the ZCS architecture, XCS can be distinguished by the following key features: an accuracy based fitness, a niche GA (acting in the action set [A]), and an adaptation of standard Q-Learning as credit assignment. Probably the most important innovation in XCS was the separation of the credit assignment component from the GA component, based on accuracy. Previous LCSs typically relied on a strength value allocated to each rule (reflecting the reward the system can expect if that rule is fired; a.k.a. reward prediction). This one strength value was used both as a measure of fitness for GA selection, and to control which rules are allowed to participate in the decision making (i.e., predictions) of the system. As a result, the GA tends to eliminate classifiers from the population that have accumulated less reward than others, which can in turn remove a low-predicting classifier that is still well suited for its environmental niche. “Wilson′s intuition was that prediction should estimate how much reward might result from a certain action, but that the evolution learning should be focused on most reliable classifiers, that is, classifiers that give a more precise (accurate) prediction” [165]. With XCS, the GA fitness is solely dependent on rule accuracy calculated separately from the other parameter values used for decision making. Although not a new idea [3, 25, 166], the accuracy-based fitness of XCS represents the starting point for a new family of LCSs, termed “accuracy-based” which are distinctly separable from the family of “strength-based” LCSs epitomized by ZCS (see Table 1). XCS is also important, because it successfully bridges the gap between LCS and RL. RL typically seeks to learn a value function which maps out a complete representation of the state/action space. Similarly, the design of XCS drives it to form an all-inclusive and accurate representation of the problem space (i.e., a complete map) rather than simply focusing on higher payoff niches in the environment (as is typically the case with strength-based LCSs). This latter methodology which seeks a rule set of efficient generalizations tends to form a best action map (or a partial map) [102, 167]. In the wake of XCS, it became clear that RL and LCS are not only linked but inherently overlapping. So much so, that analyses by Lanzi [168] led him to define LCSs as RL systems endowed with a generalization capability. “This generalization property has been recognized as the distinguishing feature of LCSs with respect to the classical RL framework” [9]. “XCS was the first classifier system to be both general enough to allow applications to several domains and simple enough to allow duplication of the presented results” [54]. As a result XCS has become the most popular LCS implementation to date, generating its own following of systems based directly on or heavily inspired by its architecture.

5.3. In the Wake of XCS

Of this following, three of the most prominent will be discussed: ACS, XCSF, and UCS. In 1998 Stolzmann introduced ACS [24] and in doing so formalized a new LCS family referred to as “anticipation-based”. “[ACS] is able to predict the perceptual consequences of an action in all possible situations in an environment. Thus the system evolves a model that specifies not only what to do in a given situation but also provides information of what will happen after a specific action was executed” [103]. The most apparent algorithmic difference in ACS is the representation of rules in the form of a condition-action-effect as opposed to the classic condition-action. This architecture can be used for multi-step problems, planning, speeding up learning, or disambiguating perceptual aliasing (where the same observation is obtained in distinct states requiring different actions). Contributing heavily to this branch of research, Martin Butz later introduced ACS2 [103] and developed several improvements to the original model [104, 118, 169–171] . For a more in depth introduction to ACS we refer the reader to [87, 172]. Another brainchild of Wilson′s was XCSF [113]. The complete action mapping of XCS made it possible to address the problem of function approximation. “XCSF evolves classifiers which represent piecewise linear approximations of parts of the reward surface associated with the problem solution” [54]. To accomplish this, XCSF introduces the concept of computed prediction, where the classifier′s prediction (i.e., predicted reward) is no longer represented by a scalar parameter value, but is instead a function calculated as a linear combination of the classifier′s inputs (for each dimension) and a weight vector maintained by each classifier. In addition to systems based on fuzzy logic, XCSF is of the minority of systems able to support continuous-valued actions. In complete contrast to the spirit of ACS, the sUpervised Classifier System (UCS) [117] was designed specifically to address single-step problem domains such as classification and data mining where delayed reward is not a concern. While XCS and the vast majority of other LCS implementations rely on RL, UCS trades this strategy for supervised learning. Explicitly, classifier prediction was replaced by accuracy in order to reflect the nature of a problem domain where the system is trained, knowing the correct prediction in advance. UCS demonstrates that a best action map can yield effective generalization, evolve more compact knowledge representations, and can converge earlier in large search spaces.

5.4. Revisiting the Pitt

While there is certainly no consensus as to which style LCS (Michigan or Pittsburgh) is “better”, the advantages of each system in the context of specific problem domains are becoming clearer [173]. Some of the more successful Pitt-style systems include GABIL [66], GALE [110], ATNoSFERES [106], MOLCS [120], GAssist [128], BioHEL [148] (a descendant of GAssist), and NAX [158] (a descendant of GALE). All but ATNoSFERES were designed primarily to address classification/data mining problems for which Pitt-style systems seem to be fundamentally suited. NAX and BioHEL both received recent praise for their human-competitive performance on moderately complex and large tasks. Also, a handful of “hybrid” systems have been developed, which merge Michigan and Pitt-style architectures (e.g., REGAL [72], GA-Miner [79], ZCCS [85], and CXCS [91]).

5.5. Visualization

There is an expanding wealth of literature beyond what we have discussed in this brief history [174]. One final innovation, which will likely prove to be of great significance to the LCS community is the design and application of visualization tools. Such tools allow researchers to follow algorithmic progress by (1) tracking online performance (i.e., by graphing metrics such as error, generality, and population size), (2) visualizing the current classifier population as it evolves (i.e., condition visualization), and (3) visualizing the action/prediction (useful in function approximation to visualize the current prediction surface) [144, 154, 175]. Examples include Holmes′s EpiXCS Workbench geared towards knowledge discovery in medical data [144], and Butz and Stalph′s cutting-edge XCSF visualization software geared towards function approximation [175, 176] and applied to robotic control in [177]. Tools such as these will advance algorithmic understandability and facilitate solution interpretation, while simultaneously fueling a continued interest in the LCS algorithm.

6. Problem Domains

The range of problem domains to which LCS has been applied can be broadly divided into three categories: function approximation problems, classification problems, and reinforcement learning problems [178]. All three domains are generally tied by the theme of optimizing prediction within an environment. Function approximation problems seek to accurately approximate a function represented by a partially overlapping set of approximation rules (e.g., a piecewise linear solution for a sine function). Classification problems seek to find a compact set of rules that classify all problem instances with maximal accuracy. Such problems frequently rely on supervised learning where feedback is provided instantly. A broad subdomain of the classification problem includes “data mining” which is the process of sorting through large amounts of data to extract or model useful patterns. Classification problems may also be divided into either Boolean or real-valued problems based on the problem type being respectively discrete, or continuous in nature. Examples of classification problems include Boolean function learning, medical diagnosis, image classification (e.g., letter recognition), pattern recognition, and game analysis. RL problems seek to find an optimal behavioral policy represented by a compact set of rules. These problems are typically distinguished by inconsistent environmental reward often requiring multiple actions before such reward is obtained (i.e., multi-step RL problem or sequential decision task). Examples of such problems would include robotic control, game strategy, environmental navigation, modeling time-dependant complex systems (e.g., stock market), and design optimization (e.g., engineering applications). Some RL problems are characterized by providing immediate reward feedback about the accuracy of a chosen class (i.e., single-step RL problem), which essentially makes it similar to a classification problem. RL problems can be partitioned further based on whether they can be modeled as a Markov decision process (MDP) or a partially observable Markov decision process (POMDP) . In short, for Markov problems the selection of the optimal action at any given time depends only on the current state of the environment and not on any past states. On the other hand, Non-Markov problems may require information on past states to select the optimal action. For a detailed introduction to this concept we refer readers to [9, 179, 180].

7. Biological Applications

One particularly demanding and promising domain for LCS application involves biological problems (e.g., epidemiology, medical diagnosis, and genetics). In order to gain insight into complex biological problems researchers often turn to algorithms which are themselves inspired by biology (e.g., genetic programming [181], ant colony optimization [182], artificial immune systems [183], and neural networks [184]). Similarly, since the mid 90s biological LCS studies have begun to appear that deal mainly with classification-type problems. One of the earliest attempts to apply an LCS algorithm to such a problem was [28]. Soon after, John Holmes initiated a lineage of LCS designed for epidemiological surveillance and knowledge discovery which included BOOLE++ [81], EpiCS [82], and most recently EpiXCS [143]. Similar applications include [93, 95, 130, 142, 185–187], all of which examined the Wisconsin breast cancer data taken from the UCI repository [188]. LCSs have also been applied to protein structure prediction [131, 149, 154], diagnostic image classification [158, 189], and promoter region identification [190].

8. Optimizing LCS

There are a number of factors to consider when trying to select or develop an “effective” LCS. The ultimate value of an LCS might be gauged by the following: (1) performance—the quality of the evolved solution (rule set), (2) scalability—how rapidly the learning time or system size grows as the problem complexity increases, (3) adaptivity—the ability of online learning systems to adapt to rapidly changing situations, and/or (4) speed—the time it takes an offline learning system to reach a “good” solution. Much of the field′s focus has been placed on optimizing performance (as defined here). The challenge of this task is in balancing algorithmic pressures designed to evolve the population of rules towards becoming what might be considered an optimal rule set. The definition of an optimal rule set is subjective, depending on the problem domain, and the system architecture. Kovacs discusses the properties of an optimal XCS rule set [O] as being correct, complete, minimal (compact), and non-overlapping [191]. Even for the XCS architecture it is not clear that these properties are always optimal (e.g., discouraging overlap prevents the evolution of default hierarchies, too much emphasis on correctness may lead to overfitting in training, and completeness is only important if the goal is to evolve a complete action map). Some of the tradeoffs are discussed in [192, 193]. Instead, researchers may use the characteristics of correctness, completeness, compactness, and overlap as metrics with which to track evolutionary learning progress. LCS, being a complex multifaceted algorithm is subject to a number of different pressures driving the rule-set evolution. Butz and Pelikan discuss 5 pressures that specifically influence XCS performance, and provide an intuitive visualization of how these pressures interact to evolve the intended complete, accurate, and maximally general problem representation [194, 195]. These include set pressure (an intrinsic generalization pressure), mutation pressure (which influences rule specificity), deletion pressure (included in set pressure), subsumption pressure (decreases population size), and fitness pressures (which generate a major drive towards accuracy). Other pressures have also been considered, including parsimony pressure for discouraging large rule sets (i.e., bloat) [196], and crowding (or niching) pressure for allocating classifiers to distinct subsets of the problem domain [42]. In order to ensure XCS success, Butz defines a number of learning bounds which address specific algorithmic pitfalls [197–200]. Broadly speaking, the number of studies addressing LCS theory are few in comparison to applications-based research. Further work in this area would certainly benefit the LCS community.

9. Component Roadmap

The following section is meant as a summary of the different LCS algorithmic components. Figure 2 encapsulates the primary elements of a generic LCS framework (heavily influenced by ZCS, XCS, and other Michigan-style systems). Using this generalized framework we identify a number of exchangeable methodologies, and direct readers towards the studies that incorporate them. Many of these elements have been introduced in Section 5, but are put in the context of the working algorithm here. It should be kept in mind that some outlying LCS implementations stray significantly from this generalized framework, and while we present these components separately, the system as a whole is dependent on the interactions and overlaps which connect them. Elements that do not obviously fit into the framework of Figure 2 will be discussed in Section 9.6. Readers interested in a simple summary and schematic of the three most renowned systems (including Holland′s standard LCS, ZCS, and XCS) are referred to [201].

9.1. Detectors and Effectors

The first and ultimately last step of an LCS iteration involves interaction with the environment. This interaction is managed by detectors and effectors [30]. Detectors sense the current state of the environment and encode it as a standard message (i.e., formatted input data). The impact of how sensors are encoded has been explored [202]. Effectors, on the other hand, translate action messages into performed actions that modify the state of the environment. For supervised learning problems, the action is supplanted by some prediction of class, and the job of effectors is simply to check that the correct prediction was made. Depending on the efficacy of the systems′ predicted action or class, the environment may eventually or immediately reward the system. As mentioned previously, the environment is the source of input data for the LCS algorithm, dependant on the problem domain being examined. “The learning capabilities of LCS rely on and are constrained by the way the agent perceives the environment, e.g., by the detectors the system employs” [52]. Also, the format of the input data may be binary, real-valued, or some other customized representation. In systems dealing with batch learning, the dataset that makes up the environment is often divided into a training and a testing set (e.g., [82]) as part of a cross-validation strategy to assess performance and ensure against overfitting.

9.2. Population

Modifying the knowledge representation of the population can occur on a few levels. First and foremost is the difference in overall population structure as embodied by the Michigan and Pitt-style families. In Michigan systems the population is made up of a single rule-set which represents the problem solution, and in Pitt systems the population is a collection of multiple competing rule-sets, each which represent a potential problem solution (see Figure 4). Next, is the overall structure of an individual rule. Most commonly, a rule is made up of a condition, an action, and one or more parameter values (typically including a prediction value and/or a fitness value) [1, 19, 22], but other structures have been explored e.g., the condition-action-effect structure used by ACSs [24]. Also worth mentioning are rule-structure-induced mechanisms, proposed to encourage the evolution of rule dependencies and internal models. Examples include: bridging-classifiers (to aid the learning of long action chains) [38, 50], tagging (a form of implicitly linking classifiers) [1, 203, 204], and classifier-chaining (a form of explicitly linking classifiers and the defining feature of a “corporate” classifier system) [85, 91]. The most basic level of rule representation is the syntax which depicts how either the condition or action is actually depicted. Many different syntaxes have been examined for representing a rule condition. The first, and probably most commonly used syntax for condition representation was fixed length bit-strings of the ternary alphabet (0,1, #) corresponding with the simple binary encoding of input data [1, 3, 19, 22]. Unfortunately, it has been shown that this type of encoding can introduce bias as well as limit the system′s ability to represent a problem solution [205]. For problems involving real-valued inputs the following condition syntaxes have been explored: real-valued alphabet [88], center-based interval predicates [92], min-max interval predicates [95], unordered-bound interval predicates [206], min-percentage representation [207], convex hulls [208], real-valued context-free grammar [155], ellipsoids [209], and hyper-ellipsoids [210]. Other condition syntaxes include: partial matching [211], value representation [203], tokens, [99, 105, 132, 134], context-free grammar [135], first-order logic expressions [212], messy conditions [213], GP-like conditions (including s-expressions) [79, 214–218], neural networks [2, 116, 219, 220], and fuzzy logic [48, 75, 77, 156, 157, 221]. Overall, advanced representations tend to improve generalization and learning, but require larger populations to do so. Action representation has seen much less attention. Actions are typically encoded in binary or by a set of symbols. Recent work has also begun to explore the prospect of computed actions, also known as computed prediction, which replaces the usual classifier action parameter with a function (e.g., XCSF function approximation) [113, 152]. Neural network predictors have also been explored [146]. Backtracking briefly, in contrast to Michigan-style systems, Pitt-style implementations tend to explore different rule semantics and typically rely on a simple binary syntax. Examples of this include: VL1 [68], CNF [66], and ADI [128, 148]. Beyond structural representation, other issues concerning the population include: (1) population initialization, (2) deciding whether to bound the population size (N), and if it is bound, (3) what value of (N) to select [129, 200].

9.3. Performance Component and Selection

This section will discuss different performance component structures and the selection mechanisms involved in covering, action selection, and the GA. The message list, a component found in many early LCSs (not included on Figure 2), is a kind of blackboard that documents the current state of the system. Acting as an interface, the message list temporarily stores all communications between the system and the environment (i.e., inputs from the detector, and classifier-posted messages that culminate as outputs to the effector) [30, 37, 59, 201]. One potential benefit of using the message list is that the LCS “can emulate memory mechanisms when a message is kept on the list over several time steps” [9]. The role of message lists will be discussed further in the context of the BBA in Section 9.4. While the match set [M] is a ubiquitous component of Michigan-style systems the action set [A] only appeared after the removal of the internal message list. [A] provided a physical location with which to track classifiers involved in sending action messages to the effector. Concurrently, a previously active action set [A] _t−1 was implemented to keep track of the last set of rules to have been placed in [A]. This temporary storage allows reward to be implicitly passed up the activating chain of rules and was aptly referred to as an implicit bucket brigade. For LCSs designed for supervised learning (e.g., NEWBOOLE [46] and UCS [117]), the sets of the performance component take on a somewhat different appearance, with [A] being replaced with a correct set [C], and not-correct set Not [C] to accommodate the different learning style. Going beyond the basic set structure, XCS also utilized a prediction array added to modify both action selection and credit assignment [22]. In brief, the prediction array calculates a system prediction P(a_j) for each action a_j represented in [M]. P(a_j) represents the strength (the likely benefit) of selecting the given a_j based on the collective knowledge of all classifiers in [M] that advocate a_j. Its purpose will become clearer in Section 9.4. Modern LCS selection mechanisms serve three main functions: (1) using the classifiers to make an action decision, (2) choosing parent rules for GA “mating”, and (3) picking out classifiers to be deleted. Four selection mechanisms are frequently implemented to perform these functions. They include: (1) purely stochastic (random) selection, (2) deterministic selection—the classifier with the largest fitness or prediction (in the case of action selection) is chosen, (3) proportionate selection (often referred to as roulette-wheel selection)—where the chances of selection are proportional to fitness, and (4) tournament selection—a number of classifiers (s) are selected at random and the one with the largest fitness is chosen. Recent studies have examined selection mechanisms and noted the advantages of tournament selection [119, 222–225]. It should be noted that when selecting classifiers for deletion, any fitness-based selection will utilize the inverse of the fitness value so as to remove less-fit classifiers. Additionally, when dealing with action selection, selection methods will rely on the prediction parameter instead of fitness. Also, it is not uncommon, especially in the case of action selection, to alternate between different selection mechanisms (e.g., MCS alternates between stochastic and deterministic schemes from one iteration to the next). Sometimes this method is referred to as the pure explore/exploit scheme [19]. While action selection occurs once per iteration, and different GA triggering mechanisms are discussed in Section 9.5, deletion occurs under the following circumstances; the global population (N) is bound, and new classifiers are being added to a population that has reached (N). At this point, a corresponding number of classifiers must be deleted. This may occur following covering (explained in Section 4) or after the GA has been triggered. Of final note is a bidding mechanism. Bidding was used by Holland′s LCS to select and allow the strongest n classifiers in [M] to post their action messages to the message list. Additionally either bidding or a conflict resolution module [52] may be advocated for action selection from the message list. A classifier′s “bid” is proportional to the product of its strength and specificity. The critical role of bidding in the BBA is discussed in the next section.

9.4. Reinforcement Component

Different LCS credit assignment strategies are bound by a similar objective (to distribute reward), but the varying specifics regarding where/when they are called, what parameters are included and updated, and what formulas are used to perform those updates have lead to an assortment of methodologies, many of which have only very subtle differences. As a result, the nomenclature used to describe an LCS credit assignment scheme is often vague (e.g., Q-Learning-Based [22]) and occasionally absent. Therefore to understand the credit assignment used in a specific system, we refer readers to the relevant primary source. Credit assignment can be as simple as updating a single value (as is implemented in MCS), or it may require a much more elaborate series of steps (e.g., BBA). We briefly review two of the most historically significant credit assignment schemes, that is, the BBA and XCS′s Q-Learning-based strategy.

9.4.1. Bucket Brigade

“The bucket brigade [BBA] may most easily be viewed as an information economy where the right to trade information is bought and sold by classifiers. Classifiers form a chain of middlemen from information manufacturer ((detectors of) the environment) to information consumer (the effectors)”—Goldberg. [8] The BBA, as described in the following lines, involves both performance and reinforcement components. The following steps outline its progression over a single time iteration (t): It should be noted that within a given (t), the message list can receive only a limited number of input messages as well as a limited number of classifier postings. Also, when a classifier posts a message to the current message list it is said to have been “activated” during (t).

(1)
Post one or more messages from the detector to the current message list [ML].
(2)
Compare all messages in [ML] to all conditions in [P] and record all matches in [M].
(3)
Post “action” messages of the highest bidding classifiers of [M] onto [ML].
(4)
Reduce the strengths of these activated classifiers {C} by the amount of their respective bids B(t) and place those collective bids in a “bucket” B_total. (paying for the privilege of posting a new message).
(5)
Distribute B_total evenly over the previously activated classifiers {C^′}. (suppliers {C^′} are rewarded for setting up a situation usable by {C}).
(6)
Replace messages in {C^′} with those in {C} and clear {C}. (updates record of previously activated classifiers).
(7)
[ML] is processed through the output interface(effector) to provoke an action.
(8)
This step occurs if a reward is returned by the environment. The reward value is added to the strength of all classifiers in {C} (the most recently activated classifiers receive the reward).

“Whenever a classifier wins a bidding competition, it initiates a transaction in which it pays out part of its strength to its suppliers and then receives similar payments from its consumers. [This] strength is a kind of capital. If a classifier receives more from its consumers than it paid out, it has made a profit, that is its strength is increased”—Holland [30]. The update for any given classifier can be summarized by the following equation where S(t) is classifier strength, B(t) is the bid of the classifier (see step 4), P(t) is the sum of all payments made to this classifier by {C} (see step 5), and R(t) is any reward received (see step 8):

()

The desired effect of this cycle is to enable classifiers to pass reward (when received) along to classifiers that may have helped make that reward possible. See [8, 38] for more details.

9.4.2. Q-Learning-Based

The Q-learning-based strategy used by XCS is an archetype of modern credit assignment. First off, it should be noted that the performance component of XCS is similar to that described for MCS (although XCS adds a prediction array and an [A] _t−1 , both imperative to the credit assignment strategy). Each classifier (j) in XCS tracks four parameters: prediction (p), prediction error (ϵ), fitness (F), and experience (e). The update of these parameters takes place in [A] _t−1 as follows.

(1)
Each rule′s ϵ is updated: ϵ_j ← ϵ_j + β(|P − p_j|) − ϵ_j).
(2)
Rule predictions are updated: p_j ← p_j + β(P − p_j).
(3)
Each rule′s accuracy is determined: κ_j = exp [(ln α)(ϵ_j − ϵ₀)/ϵ₀)] for ϵ_j > ϵ₀ otherwise 1.
(4)
A relative accuracy , is determined for each rule:
(5)
Each rule′s F is updated using : .
(6)
Increment e for all classifiers in [A].

β is a learning rate constant (0 ≤ β ≤ 1) while ϵ₀ and α are accuracy function parameters. The procedure used to calculate p, ϵ, and F is the widely implemented Widrow-Hoff formula [226] (also known as Least Mean Square) seen here:

()

An important caveat is that initially p, ϵ, and F are actually updated by respectively averaging together their current and previous values. It is only after a classifier has been adjusted at least 1/β times that the Widrow-Hoff procedure takes over parameter updates. This technique, referred to as “moyenne adaptive modifee” [227], is used to make early parameter values move more quickly to their “true” average values in an attempt at avoiding the arbitrary nature of early parameter values. The direct influence of Q-learning on this credit assignment scheme is found in the update of p_j, which takes the maximum prediction value from the prediction array, discounts it by a factor, and adds in any external reward received in the previous time. The resulting value, which Wilson calls P (see steps 1 and 2), is somewhat analogous to Q-Learning′s Q-values. Also observe that a classifier′s fitness is dependent on its ability to make accurate predictions, but is not proportional to the prediction value itself. For further perspective on basic modern credit assignment strategy see [19, 22, 228].

9.4.3. More Credit Assignment

Many other credit assignment schemes have been implemented. For example Pitt-style systems track credit at the level of entire rule sets as opposed to assigning parameters to individual rules. Supervised learning systems like UCS have basically eliminated the reinforcement component (as it is generally understood) and instead maintains and updates a single accuracy parameter [117]. Of course, many other credit assignment and parameter update strategies have been suggested and implemented. Here we list some of these strategies: epochal [3], implicit bucket brigade [44], one-step payoff-penalty [43], symmetrical payoff-penalty [46], hybrid bucket brigade-backward averaging (BB-BA) algorithm [229], nonbucket brigade temporal difference method [55], action-oriented credit assignment [230, 231], QBB [19], average reward [114], gradient descent [232, 233], eligibility traces [234], Bayesian update [147], least squares update [235], and Kalman filter update [235].

9.5. Discovery Components

A standard discovery component is comprised of a GA and a covering mechanism. The primary role of the covering mechanism is to ensure that there is at least one classifier in [P] that can handle the current input. A new rule is generated by adding some number of #′s (wild cards) at random to the input string and then selecting a random action (i.e., the new rule “0#110#0-01” might be generated from the input string 0011010) [44]. The random action assignment has been noted to aid in escaping loops [22]. The parameter value(s) of this newly generated classifier are set to the population average. Covering might also be used to initialize classifier populations on the fly, instead of starting the system with an initialized population of maximum size. The covering mechanism can be implemented differently by modifying the frequency at which #′s are added to the new rule [22, 43, 44], altering how a new rule′s parameters are calculated [19], and expanding the instances in which covering is called (e.g., ZCS will “cover” when the total strength of [M] is less than a fraction of the average seen in [P] [19]). Covering does more than just handle an unfamiliar input by assigning a random action. “Covering allows the system [to] test a hypothesis (the condition-action relation expressed by the created classifier) at the same time” [19]. The GA discovers rules by building upon knowledge already in the population (i.e., the fitness). The vast majority of LCS implementations utilize the GA as its primary discovery component. Specifically, LCSs typically use steady state GAs, where rules are changed in the population individually without any defined notion of a generation. This differs from generational GAs where all or an important part of the population is renewed from one generation to the next [9]. GAs implemented independent of an LCS are typically generational. In selecting an algorithm to address a given problem, an LCS algorithm that incorporates a GA would likely be preferable to a straightforward GA when dealing with more complex decision making tasks, specifically ones where a single rule cannot effectively represent the solution, or in problem domains where adaptive solutions are needed. Like the covering mechanism, the specifics of how a GA is implemented in an LCS may vary from system to system. Three questions seem to best summarize these differences: (1) Where is the GA applied? (2) When is GA fired? and (3) What operators does it employ? The set of classifiers to which the GA is applied can have a major impact on the evolutionary pressure it produces. While early systems applied the GA to [P] [3], the concepts of restricted mating and niching [42] moved its action to [M] and then later to [A], where it is typically applied in modern systems (see Table 1). For more on niching see [22, 42, 236, 237]. The firing of the GA can simply be controlled by a parameter (g) which represents the probability of firing the GA on a given time step (t), but in order to more fairly allocate the application of the GA to different developing niches, it can be triggered by a tracking parameter [22, 47]. Crossover and mutation are the two most recognizable operators of the GA. Both mechanisms are controlled by parameters representing their respective probabilities of being called. Historically, most early LCSs used simple one-point crossover, but interest in discovering complex “building blocks” [8, 238, 239] has led to examining two-point, uniform, and informed crossover (based on estimation of distribution algorithms) as well [239]. Additionally, a smart crossover operator for a Pitt-style LCS has also been explored [240]. The GA is a particularly important component of Pitt-style systems which relies on it as its only adaptive process. Oftentimes it seems more appropriate to classify Pitt-style systems simply as an evolutionary algorithm as opposed to what is commonly considered to be a modern LCS [9, 52]. Quite differently, the GA is absent from ACSs, instead relying on nonevolutionary discovery mechanisms [24, 99, 103, 118, 132].

9.6. Beyond the Basics

This section briefly identifies LCS implementation themes that extend beyond the basic framework such as the addition of memory, multilearning classifier systems, multiobjectivity, and data concerns. While able to deal optimally with Markov problems, the major drawback of simpler systems like ZCS and XCS was their relative inability to handle non-Markov problems. One of the methodologies that were developed to address this problem was the addition of memory via an internal register (i.e., a non-message-list memory mechanism) which can store a limited amount of information reguarding a previous state. Systems adopting memory include ZCSM [78], XCSM [83], and XCSMH [90]. Another area that has drawn attention is the development of what we will call “multilearning classifier systems” (M-LCSs) (i.e., multiagent LCSs, ensemble LCSs, and distributed LCSs), which run more than one LCS at a time. Multiagent LCSs were designed to model multiagent systems that intrinsically depend on the interaction between multiple intelligent agents (e.g., game-play) [94, 241, 242]. Ensemble LCSs were designed to improve algorithmic performance and generalization via parallelization [140–142, 153, 243–245]. Distributed LCSs were developed to assimilate distributed data (i.e. data coming from different sources) [137, 246, 247]. Similar to the concept of M-LCS, Ranawana and Palade published a detailed review and roadmap on multiclassifier systems [248]. Multiobjective LCSs discussed in [249] explicitly address the goals implicitly held by many LCS implementations (i.e., accuracy, completeness, minimalism) [97, 120]. A method that has been explored to assure minimalism is the application of a rule compaction algorithm for the removal of redundant or strongly overlapping classifiers [96, 122, 250, 251]. Some other dataset issues which have come up especially in the context of data mining include missing data [130, 252], unbalanced data [253], dataset size [254], and noise [120]. Some other interesting algorithmic innovations include partial matching [211], endogenous fitness [255], self-adapted parameters [219, 256–259], abstraction, [260], and macroclassifiers [22].

10. Conclusion

“Classifier Systems are a quagmire—a glorious, wondrous, and inventing quagmire, but a quagmire nonetheless”—Goldberg [261]. This early perspective was voiced at a time when LCSs were still quite complex and nebulously understood. Structurally speaking, the LCS algorithm is an interactive merger of other stand-alone algorithms. Therefore, its performance is dependent not only on individual components but also on the interactive implementation of the framework. The independent advancement of GA and learning theory (in and outside the context of LCS) has inspired an inovative generation of systems, that no longer merrit the label of a “quagmire”. The application of LCSs to a spectrum of problem domains has generated a diversity of implementations. However it is not yet obvious which LCSs are best suited to address a given domain, nor how to best optimize performance. The basic XCS architecture has not only revitalized interest in LCS research, but has become the model framework upon which many recent modifications or adaptations have been built. These expansions are intended to address inherent limitations in different problem domains, while sticking to a trusted and recognizable framework. But will this be enough to address relevant real-world applications? One of the greatest challenges for LCS might inevitably be the issue of scalability as the problems we look to be solved increase exponentially in size and complexity. Perhaps, as was seen pre-empting the development of ZCS and XCS, the addition of heuristics to an accepted framework might again pave the way for some novel architecture(s). Perhaps there will be a return to Holland-style architectures as the limits of XCS-based systems are reached. A number of theoretical questions should also be considered: What are the limits of the LCS framework? How will LCS take advantage of advancing computational technology? How can we best identify and interpret an evolved population (solution)? And how can we make using the algorithm more intuitive and/or interactive? Beginning with a gentle introduction, this paper has described the basic LCS framework, provided a historical review of major advancements, and provided an extensive roadmap to the problem domains, optimization, and varying components of different LCS implementations. It is hoped that by organizing many of the existing components and concepts, they might be recycled into or inspire new systems which are better adapted to a specific problem domain. The ultimate challenge in developing an optimized LCS is to design an implementation that best arranges multiple interacting components, operating in concert, to evolve an accurate, compact, comprehensible solution, in the least amount of time, making efficient use of computational power. It seems likely that LCS research may culminate in one of two ways. Either there will be some dominant core platform, flexibly supplemented by a variety of problem specific modifiers, or will there be a handful of fundamentally different systems that specialize to different problem domains. Whatever the direction, it is likely that LCS will continue to evolve and inspire methodologies designed to address some of the most difficult problems ever presented to a machine.

11. Resources

For various perspectives on the LCS algorithm, we refer readers to the following review papers [4, 7, 9, 45, 52, 54, 165, 178, 262]. Together, [45, 165] represent two decade-long consecutive summaries of current systems, unsolved problems and future challenges. For comparative system discussions see [102, 192, 263, 264]. For a detailed summary of LCS community resources as of (2002) see [265]. For a detailed examination of the design and analysis of LCS algorithms see [266].

References

1 Holland J., Hidden Order: How Adaptation Builds Complexity, 1996, Addison-Wesley, Reading, Mass, USA.
Google Scholar
2 Dam H. H., [email protected], Abbass H. A., [email protected], Lokan C., and [email protected], Yao X., [email protected], Neural-based learning classifier systems, IEEE Transactions on Knowledge and Data Engineering. (2008) 20, no. 1, 26–39, EID2-s2.0-0008154720, https://doi.org/10.1109/TKDE.2007.190671.
Google Scholar
3 Holland J. and Reitman J., D. A. Waterman and F. Inand, Cognitive systems based on adaptive agents, Pattern-Directed Inference Systems, 1978, Hayes-Roth.
Google Scholar
4 Holmes J. H., [email protected], Lanzi P. L., [email protected], Stolzmann W., and [email protected], Wilson S. W., [email protected], Learning classifier systems: new models, successful applications, Information Processing Letters. (2002) 82, no. 1, 23–30, EID2-s2.0-0008099497, https://doi.org/10.1016/S0020-0190(01)00283-6.
Google Scholar
5 Minsky M., Steps toward artificial intelligence, Proceedings of the IRE. (1961) 49, no. 1, 8–30.
Google Scholar
6 Holland J., Adaptation in Natural and Artificial Systems, 1975, University of Michigan Press, Ann Arbor, Mich, USA.
Google Scholar
7 Bull L. and Kovacs T., Foundations of Learning Classifier Systems, 2005, Springer, Berlin, Germany.
Google Scholar
8 Goldberg D., Genetic Algorithms in Search, Optimization and Machine Learning, 1989, Addison-Wesley Longman, Boston, Mass, USA.
Google Scholar
9 Sigaud O. and [email protected], Wilson S., [email protected], Learning classifier systems: a survey, Soft Computing. (2007) 11, no. 11, 1065–1078, EID2-s2.0-34249950269, https://doi.org/10.1007/s00500-007-0164-0.
Google Scholar
10 Holmes J., Learning classifier systems applied to knowledge discovery in clinical research databases, Learning Classifier Systems, from Foundations to Applications, 2000, 243–262.
Google Scholar
11 Goldberg D., The Design of Innovation: Lessons from and for Competent Genetic Algorithms, 2002, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar
12 Langley P., Elements of Machine Learning, 1996, Morgan Kaufmann, San Francisco, Calif, USA.
Google Scholar
13 Harries M. B., Sammut C., and Horn K., Extracting hidden context, Machine Learning. (1998) 32, no. 2, 101–126, https://doi.org/10.1023/A:1007420529897, EID2-s2.0-0032139819.
Google Scholar
14 Ben-David S., Kushilevitz E., and Mansour Y., Online learning versus offline learning, Machine Learning. (1997) 29, no. 1, 45–63, EID2-s2.0-0031245162.
Google Scholar
15 Sutton R. S. and Barto A., Reinforcement Learning: An Introduction, 1998, MIT Press, Cambridge, Mass, USA.
Google Scholar
16 Harmon M. and Harmon S., Reinforcement Learning: A Tutorial, December 1996.
Google Scholar
17 Wyatt J., Reinforcement learning: a brief overview, Foundations of Learning Classifier Systems, 2005, 179–202.
Google Scholar
18 Bull L., Two simple learning classifier systems, Foundations of Learning Classifier Systems, 2005, 63–89.
Google Scholar
19 Wilson S. W., ZCS: a zeroth level classifier system, Evolutionary Computation. (1994) 2, no. 1, 1–18.
Google Scholar
20 Goldberg D., Computer-aided gas pipeline operation using genetic algorithms and machine learning, Ph.D. thesis, 1983, Department Civil Engineering, University of Michigan, Ann Arbor, Mich, USA.
Google Scholar
21 Baker J., Reducing bias and inefficiency in the selection algorithm, Proceedings of the 2nd International Conference on Genetic Algorithms on Genetic Algorithms and Their Application, 1987, 14–21.
Google Scholar
22 Wilson S. W., Classifier fitness based on accuracy, Evolutionary Computation. (1995) 3, no. 2, 149–175.
Google Scholar
23 Smith S., A learning system based on genetic adaptive algorithms, Ph.D. thesis, 1980, University of Pittsburgh, Pittsburgh, Pa, USA.
Google Scholar
24 Stolzmann W., Anticipatory classifier systems, Proceedings of the 3rd Annual Genetic Programming Conference, 1998, 658–664.
Google Scholar
25 Holland J., Adaptation, Progress in Theoretical Biology. (1976) 4, 263–293.
Google Scholar
26 Robertson G. G. and Riolo R. L., A tale of two classifier systems, Machine Learning. (1988) 3, no. 2-3, 139–159, https://doi.org/10.1007/BF00113895, EID2-s2.0-0013667772.
Google Scholar
27 Smith S., Flexible learning of problem solving heuristics through adaptive search, Proceedings of the 8th International Joint Conference on Artificial Intelligence, 1983, 422–425.
Google Scholar
28 Congdon C., A comparison of genetic algorithms and other machine learning systems of a complex classification task from common disease research, Ph.D. thesis, 1995, University of Michigan.
Google Scholar
29 Riolo R., Empirical studies of default hierarchies and sequences of rules in learning classifier systems, Doctoral dissertation, 1988, University of Michigan, Ann Arbor, Mich, USA.
Google Scholar
30 Holland J., Escaping brittleness: the possibilities of general-purpose learning algorithms applied to parallel rule-based systems, Machine Learning. (1986) 2, 593–623.
Google Scholar
31 Holland J., A mathematical framework for studying learning in classifier systems, Physica D. (1986) 2, no. 1–3, 307–317.
Google Scholar
32 Holland J. H., Adaptive algorithms for discovering and using general patterns in growing knowledge bases, International Journal of Policy Analysis and Information Systems. (1980) 4, no. 3, 245–268, EID2-s2.0-0019060894.
Google Scholar
33 Holland J., Adaptive knowledge acquisition, unpublished research proposal, 1980.
Google Scholar
34 Holland J., Genetic algorithms and adaptation, 1981, no. 34, Department of Computer and Communication Sciences, University of Michigan, Ann Arbor, Mich, USA.
Google Scholar
35 Holland J., Induction in artificial intelligence, 1983, Department of Computer and Communication Sciences, University of Michigan, Ann Arbor, Mich, USA.
Google Scholar
36 Holland J., A more detailed discussion of classifier systems, 1983, Department of Computer and Communication Sciences, University of Michigan, Ann Arbor, Mich, USA.
Google Scholar
37 Holland J., Genetic algorithms and adaptation, Adaptive Control of Ill-Defined Systems, 1984, 317–333.
10.1007/978-1-4684-8941-5_21
Google Scholar
38 Holland J., Properties of the Bucket brigade, Proceedings of the 1st International Conference on Genetic Algorithms, 1985, 1–7.
Google Scholar
39 Holland J., A mathematical framework for studying learning in classifier systems, Research Memo, 1985, no. RIS-25r, The Rowland Institute for Science, Cambridge, Mass, USA.
Google Scholar
40 Holland J., Genetic algorithms and classifier systems: foundations and future directions, Proceedings of the 2nd International Conference on Genetic Algorithms and Their Application, 1987, 82–89.
Google Scholar
41 Samuel A., Some studies in machine learning using the game of checkers, IBM Journal of Research and Development. (1959) 211–232.
Google Scholar
42 Booker L. B., Intelligent behavior as an adaptation to the task environment, 1982.
Google Scholar
43 Wilson S. W., Classifier systems and the animat problem, Machine Learning. (1987) 2, no. 3, 199–228, https://doi.org/10.1007/BF00058679, EID2-s2.0-0000874753.
Google Scholar
44 Wilson S. W., Knowledge growth in an artificial animal, Proceedings of the 1st International Conference on Genetic Algorithms and Their Application, 1985, 16–23.
Google Scholar
45 Wilson S. W. and Goldberg D., A critical review of classifier systems, Proceedings of the 3rd International Conference on Genetic Algorithms and Their Application, 1989, 244–255.
Google Scholar
46 Bonelli P., Parodi A., Sen S., and Wilson S., NEWBOOLE: a fast GBML system, Proceedings of the 7th International Conference on Machine Learning, 1990, 153–159.
Google Scholar
47 Booker L., Triggered rule discovery in classifier systems, Proceedings of the 3rd International Conference on Genetic Algorithms, 1989, 265–274.
Google Scholar
48 Valenzuela-Rendon M., The fuzzy classifier system: a classifier system for continuously varying variables, Proceedings of the 4th International Conference on Genetic Algorithm, 1991, 346–353.
Google Scholar
49 Bonarini A., An introduction to learning fuzzy classifier systems, 1813, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′00), 2000, 83–104, Lecture Notes in Artificial Intelligence.
Google Scholar
50 Riolo R., Bucket brigade performance: I. Long sequences of classifiers, Proceedings of the 2nd International Conference on Genetic Algorithms and Their Application, 1987, Mahwah, NJ, USA, Lawrence Erlbaum, 184–195.
Google Scholar
51 Riolo R., Bucket brigade performance: II. Default hierarchies, Proceedings of the 2nd International Conference on Genetic Algorithms and Their Application, 1987, Mahwah, NJ, USA, Lawrence Erlbaum, 196–201.
Google Scholar
52 Lanzi P. and Riolo R., Recent trends in learning classifier systems research, Advances in Evolutionary Computing: Theory and Applications, 2003, 955–988, Natural Computing Series.
Google Scholar
53 Barry A., Hierarchy formation within classifier systems: a review, Proceedings of the 1st International Conference on Evolutionary Algorithms and Their Application (EVCA ′96), 1996, 195–211.
Google Scholar
54 Lanzi P. L., Learning classifier systems: then and now, Evolutionary Intelligence. (2008) 1, no. 1, 63–82.
Google Scholar
55 Riolo R., Lookahead planning and latent learning in a classifier system, Proceedings of the 1st International Conference on Simulation of Adaptive Behavior on from Animals to Animats, 1991, 316–326.
Google Scholar
56 Schaffer J. and Grefenstette J., Multi-objective learning via genetic algorithms, Proceedings of the 9th International Joint Conference on Artificial Intelligence, 1985, 593–595.
Google Scholar
57 Greene D., J. DeGross and C. Kriebel, Automated knowledge acquisition: overcoming the expert system bottleneck, Proceedings of the 8th International Conference on Information Systems, 1987, Pittsburgh, Pa, USA, 107–117.
Google Scholar
58 Grefenstette J. J., Credit assignment in rule discovery systems based on genetic algorithms, Machine Learning. (1988) 3, no. 2-3, 225–245, https://doi.org/10.1007/BF00113898, EID2-s2.0-0000146518.
Google Scholar
59 Booker L. B., Classifier systems that learn internal world models, Machine Learning. (1988) 3, no. 2-3, 161–192, https://doi.org/10.1007/BF00113896, EID2-s2.0-0001570452.
Google Scholar
60 Grefenstette J., Incremental learning of control strategies with genetic algorithms, Proceedings of the 6th International Workshop on Machine Learning, 1989, 340–344.
Google Scholar
61 Grefenstette J., The evolution of strategies for multiagent environments, Adaptive Behavior. (1992) 1, no. 1.
Google Scholar
62 Grefenstette J., The User′s Guide to SAMUEL-97: An Evolutionary Learning System, 1997, Navy Center for Applied Research in Artificial Intelligence, Naval Research Laboratory, Washington, DC, USA.
Google Scholar
63 Shu L. and Schaeffer J., HCS: adding hierarchies to classifier systems, Proceedings of the 4th International Conference on Genetic Algorithms and Their Application, 1991, 339–345.
Google Scholar
64 Dorigo M. and Sirtori E., Alecsys: a parallel laboratory for learning classifier systems, Proceedings of the 4th International Conference on Genetic Algorithms, 1991.
Google Scholar
65 Dorigo M., [email protected], Alecsys and the autonoMouse: learning to control a real robot by distributed classifier systems, Machine Learning. (1995) 19, no. 3, 209–240, EID2-s2.0-0029326107, https://doi.org/10.1007/BF00996270.
Google Scholar
66 De Jong K. and Spears W., Learning concept classification rules using genetic algorithms, 2, Proceedings of the 12th International Conference on Artificial Intelligence (IJCAI ′91), 1991.
Google Scholar
67 De Jong K. A., [email protected], Spears W. M., and [email protected], Gordon D. F., [email protected], Using genetic algorithms for concept learning, Machine Learning. (1993) 13, no. 2-3, 161–188, EID2-s2.0-0027696338, https://doi.org/10.1007/BF00993042.
Google Scholar
68 Janikow C., Inductive Learning of decision rules in attribute-based examples: a knowledge-intensive genetic algorithm approach, Ph.D. thesis, 1991, University of North Carolina.
Google Scholar
69 Janikow C. Z., [email protected], A knowledge-intensive genetic algorithm for supervised learning, Machine Learning. (1993) 13, no. 2-3, 189–228, EID2-s2.0-0027696178, https://doi.org/10.1007/BF00993043.
Google Scholar
70 Greene D., Inductive knowledge acquisition using genetic adaptive search, Ph.D. thesis, 1992.
Google Scholar
71 Greene D. P. and [email protected], Smith S. F., [email protected], Competition-based induction of decision models from examples, Machine Learning. (1993) 13, no. 2-3, 229–257, EID2-s2.0-0027696043, https://doi.org/10.1007/BF00993044.
Google Scholar
72 Giordana A. and Saitta L., REGAL: an integrated system for learning relations using genetic algorithms, Proceedings of the 2nd International Workshop on Multistrategy Learning, 1993, 234–249.
Google Scholar
73 Giordana A., Saitta L., and Zini F., Learning disjunctive concepts with distributed genetic algorithms, 1, Proceedings of the 1st IEEE Conference on Evolutionary Computation, June 1994, Orlando, Fla, USA, 115–119, EID2-s2.0-0028552879.
Google Scholar
74 Giordana A. and Neri F., Search-intensive concept induction, Evolutionary Computation. (1995) 3, no. 4, 375–416.
Google Scholar
75 Bonarini A., ELF: learning incomplete fuzzy rule sets for an autonomous robot, Proceedings of the ELITE Foundation (EUFIT ′93), 1993, Aachen, Germany, 69–75.
Google Scholar
76 Bonarini A., R. Trappl, Some methodological issues about designing autonomous agents which learn their behaviors: the ELF experience, Proceedings of the Cybernetics and Systems Research, 1994, 1435–1442.
Google Scholar
77 Bonarini A., Evolutionary learning of fuzzy rules: competition and cooperation, Fuzzy Modelling: Paradigms and Practice, 1996, 265–284.
Google Scholar
78 Cliff D. and Ross S., Adding memory to ZCS, Adaptive Behavior. (1994) 3, no. 2, 101–150.
Google Scholar
79 Flockhart I. and Radcliffe N., GA-MINER: parallel data mining with hierarchical genetic algorithms-final report, EPCC AIKMS GA-Miner-Report, no. 1.
Google Scholar
80 Flockhart I., Radcliffe N., Simoudis E., Han J., and Fayyad U., A genetic algorithm-based approach to data mining, Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining (KDD ′96), 1996, 299–302.
Google Scholar
81 Holmes J., A genetics-based machine learning approach to knowledge discovery in clinical data, Proceedings of the AMIA Anual Symposim, 1996, 883–883.
Google Scholar
82 Holmes J., Discovering risk of disease with a learning classifier system, Proceedings of the 7th International Conference on Genetic Algorithms (ICGA ′97), 1997, 426–433.
Google Scholar
83 Lanzi P., Adding memory to XCS, Proceedings of IEEE Conference on Evolutionary Computation (ICEC ′98), 1998, 609–614, EID2-s2.0-0031650016.
Google Scholar
84 Lanzi P., An analysis of the memory mechanism of XCSM, Genetic Programming. (1998) 98, 643–651.
Google Scholar
85 Tomlinson A. and Bull L., A corporate classifier system, 1998, 550–559, Lecture Notes in Computer Science.
Google Scholar
86 Tomlinson A. and Bull L., A zeroth level corporate classifier system, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′99), 1999, 306–313.
Google Scholar
87 Stolzmann W., An introduction to anticipatory classifier systems, Learning Classifier Systems: From Foundations to Applications, 2000, 175–194, Lecture Notes in Computer Science.
Google Scholar
88 Browne W., The Development of an Industrial Learning Classifier System for Application to a Steel Hot Strip Mill, Ph.D. thesis, 1999, Division of Mechanical Engineering and Energy Studies, University of Wales, Cardiff, UK.
Google Scholar
89 Browne W. N. L., Holford K. M., [email protected], Moore C. J., and Bullock J., An industrial learning classifier system: the importance of pre-processing real data and choice of alphabet, Engineering Applications of Artificial Intelligence. (2000) 13, no. 1, 25–36, EID2-s2.0-0002447833, https://doi.org/10.1016/S0952-1976(99)00034-2.
Google Scholar
90 Lanzi P. and Wilson S., Toward optimal classifier system performance in non-Markov environments, Evolutionary Computation. (2000) 8, no. 4, 393–418.
Google Scholar
91 Tomlinson A. and Bull L., A corporate XCS, Proceedings of the International Workshop on Learning Classifier Systems, 2000, 195–208, Lecture Notes in Computer Science.
Google Scholar
92 Wilson S. W., Get real! XCS with continuous-valued inputs, Proceedings of the 3rd International Workshop on Advances in Learning Classifier Systems, 2000, 209–222, Lecture Notes in Computer Science.
Google Scholar
93 Walter D. and Mohan C. K., ClaDia: a fuzzy classifier system for disease diagnosis, 2, Proceedings of the IEEE Conference on Evolutionary Computation (ICEC ′00), 2000, 1429–1435, EID2-s2.0-0033676167.
Google Scholar
94 Takadama K., Terano T., and Shimohara K., L. Lanzi, W. Stolzmann, and S. W. Wilson, Learning classifier systems meet multiagent environments, Proceedings of the 3rd International Workshop on Learning Classifier Systems (IWLCS ′00), 2000, Springer, 192–210.
Google Scholar
95 Wilson S. W., Mining oblique data with XCS, Proceedings of the 3rd International Workshop on Advances in Learning Classifier Systems, 2000, 158–176.
Google Scholar
96 Wilson S. W., Compact rulesets from XCSI, Proceedings of the 4th International Workshop on Advances in Learning Classifier Systems, 2001, 197–210.
Google Scholar
97 Bernado-Mansilla E. and Garrell-Guiu J., MOLeCS: a multiObjective learning classifier system, 1, Proceedings of the Conference on Genetic and Evolutionary Computation, 2000.
Google Scholar
98 Mansilla E. and Guiu J., MOLeCS: using multiobjective evolutionary algorithms for learning, Proceedings of the 1st International Conference on Evolutionary Multi-Criterion Optimization, 2001, 696–710, Lecture Notes in Computer Science.
Google Scholar
99 Gérard P. and Sigaud O., YACS: combining dynamic programming with generalization in classifiersystems, Proceedings of the 3rd International Workshop on Advances in Learning Classifier Systems (IWLCS ′00), 2000, 52–69.
Google Scholar
100 Gérard P., Stolzmann W., and Sigaud O., YACS : a new learning classifier system using anticipation, Soft Computing-A. (2002) 6, no. 3, 216–228.
Google Scholar
101 Kovacs T., A comparison of strength and accuracy-based fitness in learning classifier systems, Ph.D. thesis, 2001, University of Birmingham, Birmingham, UK.
Google Scholar
102 Kovacs T., Two views of classifier systems, Advances in Learning Classifier Systems, 2002, 74–87, Lecture Notes in Computer Science, https://doi.org/10.1007/3-540-48104-4_6.
Google Scholar
103 Butz M., Biasing exploration in an anticipatory learning classifier system, 2321, Proceedings of the 4th International Workshop on Advances in Learning Classifier Systems, 2001, 3–22, Lecture Notes in Computer Science.
Google Scholar
104 Butz M. V. and [email protected], Hoffmann J., [email protected], Anticipations control behavior: animal behavior in an anticipatory learning classifier system, Adaptive Behavior. (2002) 10, no. 2, 75–96, EID2-s2.0-0035350726, https://doi.org/10.1177/1059712302010002001.
Google Scholar
105 Picault S. and Landau S., ATNoSFERES: a Darwinian evolutionary model for individual or collective agent behavior, 2001, LIP6, Paris, France.
Google Scholar
106 Landau S., Picault S., and Drogoul A., ATNoSFERES: a model for evolutive agent behaviors, 1, Proceedings of the Symposium on Adaptive Agents and Multi-Agent Systems (AISB ′01), 2001.
Google Scholar
107 Landau S., Picault S., Sigaud O., and Gérard P., A comparison between ATNoSFERES and XCSM, Proceedings of the Genetic and Evolutionary Computation Conference, 2002, 926–933.
Google Scholar
108 Landau S., Picault S., Sigaud O., and Gerard P., Further comparison between ATNoSFERES and XCSM, 2661, Proceedings of the 5th International Workshop on Learning Classifier Systems, 2003, 99–117, Lecture Notes in Computer Science, EID2-s2.0-0346955730.
Google Scholar
109 Landau S., [email protected], Sigaud O., [email protected], Picault S., and [email protected], Gerard P., [email protected], An experimental comparison between ATNoSFERES and ACS, 4399, Proceedings of the International Workshop on Learning Classifier Systems, 2007, 144–160, Lecture Notes in Computer Science, EID2-s2.0-0031215211.
Google Scholar
110 Llorà X., Garrell J. et al., Knowledge-independent data mining with fine-grained parallel evolutionary algorithms, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′01), 2001, San Francisco, Calif, USA, Morgan Kaufmann, 461–468.
Google Scholar
111 Kovacs T., Genetic based machine learning using fine-grained parallelism for data mining, Ph.D. thesis, 2002, Enginyeria i Arquitectura La Salle, Ramon Llull University.
Google Scholar
112 Llorà X. and Guiu J., Coevolving different knowledge representations with fine-grained parallel learning classifier systems, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′02), 2002, San Francisco, Calif, USA, Morgan Kaufmann, 934–941.
Google Scholar
113 Wilson S. W., Classifiers that approximate functions, Natural Computing. (2002) 1, no. 2, 211–234.
Google Scholar
114 Tharakunnel K. and Goldberg D., XCS with average reward criterion in multi-step environment, 2002, Illinois Genetic Algorithms Laboratory (IlliGAL), Department of General Engineering, University of Illinois at Urbana-Champaign.
Google Scholar
115 Hurst J., Bull L., and Melhuish C., TCS learning classifier system controller on a real robot, Proceedings of the 7th International Conference on Parallel Problem Solving from Nature (PPSN ′02), September 2002, Granada, Spain, 588–600, Lecture Notes in Computer Science.
Google Scholar
116 Bull L. and O′Hara T., Accuracy-based neuro and neuro-fuzzy classifier systems, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′02), 2002, 905–911.
Google Scholar
117 Bernadó-Mansilla E. and Garrell-Guiu J. M., Accuracy-based learning classifier systems: models, analysis and applications to classification tasks, Evolutionary Computation. (2003) 11, no. 3, 209–238, https://doi.org/10.1162/106365603322365289.
Google Scholar
118 Butz M. and Goldberg D., Generalized state values in an anticipatory learning classifier system, Proceedings of the 7th International Conference on Simulation of Adaptive Behavior in Anticipatory Learning Systems, 2003, 282–302, Lecture Notes in Computer Science.
Google Scholar
119 Butz M., Sastry K., and Goldberg D., Tournament selection: stable fitness pressure in XCS, Proceedings of the Genetic and Evolutionary Computation Conference, 2003, 1857–1869, Lecture Notes in Computer Science.
Google Scholar
120 Llorà X. and [email protected], Goldberg D. E., [email protected], Bounding the effect of noise in multiobjective learning classifier systems, Evolutionary Computation. (2003) 11, no. 3, 279–298, EID2-s2.0-0001387704.
Google Scholar
121 Bull L., A simple accuracy-based learning classifier system, Learning Classifier Systems Group Technical Report, 2003, no. UWELCSG03-005, University of the West of England, Bristol, UK.
Google Scholar
122 Dixon P. W., Corne D. W., and Oates M. J., A ruleset reduction algorithm for the XCS learning classifier system, Learning Classifier Systems, 2003, 2661, 20–29, Lecture Notes in Computer Science, EID2-s2.0-7044239082.
Google Scholar
123 Bull L., Lookahead and latent learning in a simple accuracy-based classifier system, Proceedings of the 8th International Conference on Parallel Problem Solving from Nature, 2004, 1042–1050, Lecture Notes in Computer Science.
Google Scholar
124 Gaspar A. and Hirsbrunner B., PICS: Pittsburgh immune classifier system, Proceedings of the AISB Symposium on the Immune System and Cognition, March 2004, Leeds, UK.
Google Scholar
125 Gaspar A. and Hirsbrunner B., From optimization to learning in changing environments: the Pittsburgh immune classifier system, Proceedings of the 1st International Conference on Artificial Immune Systems (ICARIS ′02), September 2002.
Google Scholar
126 Hurst J. and Bull L., A self-adaptive neural learning classifier system with constructivism for mobile robot control, Proceedings of the 8th International Conference on Parallel Problem Solving from Nature (PPSN ′04), September 2004, Birmingham, UK, 942–951, Lecture Notes in Computer Science.
Google Scholar
127 Bull L., A simple payoff-based learning classifier system, Proceedings of the 8th International Conference on Parallel Problem Solving from Nature, 2004, 1032–1041, Lecture Notes in Computer Science.
Google Scholar
128 Bacardit J., Pittsburgh genetic-based machine learning in the data mining era: representations, generalization, and run-time, Ph.D. thesis, 2004, Enginyeria i Arquitectura La Salle, Ramon Llull University, Barcelona, European Union, Catalonia, Spain.
Google Scholar
129 Bacardit J., Analysis of the initialization stage of a Pittsburgh approach learning classifier system, Proceedings of the Conference on Genetic and Evolutionary Computation, 2005, 1843–1850.
Google Scholar
130 Bacardit J. and Butz M., Data mining in learning classifier systems: comparing XCS with GAssist, 4399, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′07), 2007, 282–290, Lecture Notes in Computer Science.
Google Scholar
131 Stout M., [email protected], Bacardit J., [email protected], Hirst J. D., [email protected], Smith R. E., and [email protected], Krasnogor N., [email protected], Prediction of topological contacts in proteins using learning classifier systems, Soft Computing. (2009) 13, no. 3, 245–258, EID2-s2.0-17444368331, https://doi.org/10.1007/s00500-008-0318-8.
Google Scholar
132 Gérard P., Meyer J.-A., and Sigaud O., Combining latent learning with dynamic programming in the modular anticipatory classifier system, European Journal of Operational Research. (2005) 160, no. 3, 614–637, https://doi.org/10.1016/j.ejor.2003.10.004, EID2-s2.0-4444312064.
Google Scholar
133 Hamzeh A. and Rahmani A., An evolutionary function approximation approach to compute prediction in XCSF, 3720, Proceedings of the 16th European Conference on Machine Learning (ECML ′05), October 2005, Porto, Portugal, 584–592, Lecture Notes in Computer Science, https://doi.org/10.1007/11564096_57, EID2-s2.0-33646386390.
Google Scholar
134 Landau S., Sigaud O., and Schoenauer M., ATNoSFERES revisited, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′05), 2005, 1867–1874.
Google Scholar
135 Unold O., Context-free grammar induction with grammar-based classifier system, Archives of Control Science. (2005) 15, no. 4.
Google Scholar
136 Unold O. and Cielecki L., Grammar-based classifier system, Issues in Intelligent Systems: Paradigms, 2005, EXIT, Warsaw, Poland, 273–286.
Google Scholar
137 Dam H., Abbass H., and Lokan C., DXCS: an XCS system for distributed data mining, Proceedings of the Conference on Genetic and Evolutionary Computation, 2005, 1883–1890.
Google Scholar
138 Dam H., Abbass H., and Lokan C., Investigation on DXCS: an XCS system for distribution data mining, with continuous-valued inputs in static and dynamic environments, Proceedings of the IEEE Cogress on Evolutionary Computation, 2005.
Google Scholar
139 Dam H., Abbass H., and Lokan C., The performance of the DXCS system on continuous-valued inputs in stationary and dynamic environments, 1, Proceedings of the IEEE Congress on Evolutionary Computation, 2005.
Google Scholar
140 Gao Y., Huang J., Rong H., and Gu D., Learning classifier system ensemble for data mining, Proceedings of the Workshops on Genetic and Evolutionary Computation, 2005, 63–66.
Google Scholar
141 Gao Y., [email protected], Wu L., and Huang J., [email protected], Ensemble learning classifier system and compact ruleset, 4247, Proceedings of the 6th International Conference Simulated Evolution and Learning (SEAL ′06), October 2006, Hefei, China, 42–49, Lecture Notes in Computer Science, EID2-s2.0-0042643357.
Google Scholar
142 Gao Y., [email protected], Huang J. Z., [email protected], Rong H., and [email protected], Gu D.-Q., LCSE: learning classifier system ensemble for incremental medical instances, 4399, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′07), 2007, 93–103, Lecture Notes in Computer Science, EID2-s2.0-0032645080.
Google Scholar
143 Holmes J. H. and [email protected], Sager J. A., [email protected], Rule discovery in epidemiologic surveillance data using EpiXCS: an evolutionary computation approach, 3581, Proceedings of the 10th Conference on Artificial Intelligence in Medicine (AIME ′05), July 2005, Aberdeen, Scotland, 444–452, Lecture Notes in Computer Science, EID2-s2.0-0001387704.
Google Scholar
144 Holmes J. H. and [email protected], Sager J. A., [email protected], The EpiXCS workbench: a tool for experimentation and visualization, 4399, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′07), 2007, 333–344, Lecture Notes in Computer Science, EID2-s2.0-0037089741.
Google Scholar
145 Holmes J. H., [email protected], Detection of sentinel predictor-class associations with XCS: a sensitivity analysis, 4399, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′07), 2007, 270–281, Lecture Notes in Computer Science, EID2-s2.0-0003016876.
Google Scholar
146 Loiacono D. and Lanzi P., Evolving neural networks for classifier prediction with XCSF, Proceedings of the Workshop on Evolutionary Computation (ECAI ′06), 2006, 36–40.
Google Scholar
147 Dam H., Abbass H., and Lokan C., BCS: a Bayesian learning classifier system, 2006, no. TR-ALAR-200604005, The Artificial Life and Adaptic Robotics Laboratory, School of Information Technology and Electrical Engineering, University of New South Wales, Cardiff, UK.
Google Scholar
148 Bacardit J. and Krasnogor N., Biohel: bioinformatics-oriented hierarchical evolutionary learning (Nottingham ePrints), 2006, University of Nottingham, Nottingham, UK.
Google Scholar
149 Bacardit J., Stout M., Hirst J. D., Sastry K., Llorà X., and Krasnogor N., Automated alphabet reduction method with evolutionary algorithms for protein structure prediction, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 346–353, https://doi.org/10.1145/1276958.1277033, EID2-s2.0-34548056763.
Google Scholar
150 Hamzeh A. and [email protected], Rahmani A., [email protected], Extending XCSFG beyond linear approximation, Proceedings of the IEEE Congress on Evolutionary Computation (CEC ′06), July 2006, Vancouver, Canada, 2246–2253, EID2-s2.0-27144549349.
Google Scholar
151 Hamzeh A. and [email protected], Rahmani A., [email protected], A new architecture of XCS to approximate real-valued functions based on high order polynomials using variable-length GA, 3, Proceedings of the 3rd International Conference on Natural Computation (ICNC ′07), August 2007, Haikou, China, 515–519, EID2-s2.0-32444436359, https://doi.org/10.1109/ICNC.2007.86.
Google Scholar
152 Lanzi P. and Loiacono D., Classifier systems that compute action mappings, Proceedings of the 9th Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 1822–1829, https://doi.org/10.1145/1276958.1277322, EID2-s2.0-34548098394.
Google Scholar
153 Gershoff M. and Schulenburg S., Collective behavior based hierarchical XCS, Proceedings of the Conference on Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 2695–2700, https://doi.org/10.1145/1274000.1274064, EID2-s2.0-34548063976.
Google Scholar
154 Smith R. E. and [email protected], Jiang M. K., [email protected], MILCS: a mutual information learning classifier system, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 2945–2952, EID2-s2.0-34548097500, https://doi.org/10.1145/1274000.1274063.
Google Scholar
155 Cielecki L. and Unold O., GCS with real-valued input, 4527, Proceedings of the 2nd International Work-Conference on The Interplay between Natural and Artificial Computation, 2007, 488–497, Lecture Notes in Computer Science.
Google Scholar
156 Casillas J. and [email protected], Bull L., [email protected], Fuzzy-XCS: a Michigan genetic fuzzy system, IEEE Transactions on Fuzzy Systems. (2007) 15, no. 4, 536–550, EID2-s2.0-0030661435, https://doi.org/10.1109/TFUZZ.2007.900904.
Google Scholar
157 Orriols-Puig A., [email protected], Casillas J., and [email protected], Bernadó-Mansilla E., [email protected], Fuzzy-UCS: preliminary results, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, 2871–2874, EID2-s2.0-0000259511, https://doi.org/10.1145/1274000.1274059.
Google Scholar
158 Llorà X., Reddy R., Matesic B., and Bhargava R., Towards better than human capability in diagnosing prostate cancer using infrared spectroscopic imaging, Proceedings of the 9th Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 2098–2105, https://doi.org/10.1145/1276958.1277366, EID2-s2.0-34548100580.
Google Scholar
159 Sutton R. S., [email protected], Introduction: the challenge of reinforcement learning, Machine Learning. (1992) 8, no. 3-4, 225–227, EID2-s2.0-34249831562, https://doi.org/10.1007/BF00992695.
Google Scholar
160 Sutton R. S., Learning to predict by the methods of temporal differences, Machine Learning. (1988) 3, no. 1, 9–44, https://doi.org/10.1007/BF00115009, EID2-s2.0-33847202724.
Google Scholar
161 Watkins C., Learning from Delayed Rewards, 1989.
Google Scholar
162 Liepins G., Hilliard M., Palmer M., and Rangarajan G., Alternatives for classifier system credit assignment, Proceedings of the 11th International Joint Conference on Artificial Intelligence (IJCAI ′89), 1989, 756–761.
Google Scholar
163 Dorigo M. and Bersini H., A comparison of Q-learning and classifier systems, Proceedings of the 3rd International Conference on Simulation of Adaptive Behavior: From Animals to Animats 3, 1994, Cambridge, Mass, USA, MIT Press, 248–255.
Google Scholar
164 Dorigo M., Genetic and non-genetic operators in ALECSYS, Evolutionary Computation. (1993) 1, no. 2, 151–164.
Google Scholar
165 Lanzi P. and Riolo R., A roadmap to the last decade of learning classifier system research(from 1989 to 1999), Proceedings of the International Workshop on Learning Classifier Systems, 2000, 33–61, Lecture Notes in Computer Science.
Google Scholar
166 Frey P. W. and Slate D. J., Letter recognition using Holland-style adaptive classifiers, Machine Learning. (1991) 6, no. 2, 161–182, EID2-s2.0-0026120634, https://doi.org/10.1007/BF00114162.
Google Scholar
167 Kovacs T., A comparison of strength and accuracy-based fitness in learning classifier systems, Ph.D. thesis, 2002, University of Birmingham, Birmingham, UK.
Google Scholar
168 Lanzi P., Learning classifier systems from a reinforcement learning perspective, Soft Computing. (2002) 6, no. 3, 162–170.
Google Scholar
169 Butz M., Goldberg D., and Stolzmann W., Introducing a genetic generalization pressure to the anticipatory classier system: part 1-theoretical approach, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′00), 2000.
Google Scholar
170 Butz M., Goldberg D., and Stolzmann W., Investigating generalization in the anticipatory classifier system, Proceedings of the 6th International Conference on Parallel Problem Solving from Nature, 2000, 735–744, Lecture Notes in Computer Science.
Google Scholar
171 Butz M., Goldberg D., and Stolzmann W., Probability-enhanced predictions in the anticipatory classifier system, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′00), 2000, Springer, 37–51.
Google Scholar
172 Butz M., Anticipatory Learning Classifier Systems, 2002, Kluwer Academic Publishers, Dordrecht, The Netherlands.
Google Scholar
173 Bacardit J. and Butz M., Data mining in learning classifier systems: comparing XCS with GAssist, Proceedings of the 7th International Workshop on Learning Classifier Systems (IWLCS ′04), 2004.
Google Scholar
174 Kovacs T. and Lanzi P., A learning classifier systems bibliography, 1999, CSR Centre, School of Computer Science Research, University of Birmingham, Birmingham, UK.
Google Scholar
175 Stalph P. and Butz M., Documentation of XCSF-Ellipsoids Java plus Visualization.
Google Scholar
176 Butz M., Documentation of XCSFJava 1.1 plus visualization, MEDAL Report, 2007, no. 2007008.
Google Scholar
177 Butz M. and Herbort O., Context-dependent predictions and cognitive arm control with XCSF, Proceedings of the 10th Annual Conference on Genetic and Evolutionary Computation, 2008, New York, NY, USA, ACM, 1357–1364.
Google Scholar
178 Butz M., Combining gradient-based with evolutionary online learning: an introduction to learning classifier systems, Proceedings of the 7th International Conference on Hybrid Intelligent Systems (HIS ′07), 2007, 12–17.
Google Scholar
179 Russell S., Norvig P., Canny J., Malik J., and Edwards D., Artificial Intelligence: A Modern Approach, 1995, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
180 Butz M., Rule-based Evolutionary Online Learning Systems: A Principled Approach to LCS Analysis And Design, 2006, Springer, Berlin, Germany.
Google Scholar
181 Koza J., Genetic Programming: On the Programming of Computers by Means of Natural Selection, 1992, MIT Press, Cambridge, Mass, USA.
Google Scholar
182 Dorigo M. and Stützle T., Ant Colony Optimization, 2004, MIT Press, Cambridge, Mass, USA.
Google Scholar
183 De Castro L. and Timmis J., Artificial Immune Systems: A New Computational Intelligence Approach, 2002, Springer, New York, NY, USA.
Google Scholar
184 Haykin S., Neural Networks: A Comprehensive Foundation, 1998, Prentice-Hall, Upper Saddle River, NJ, USA.
Google Scholar
185 Bernado E., Llorà X., and Garrell J., XCS and GALE: a comparative study of two learning classifier systems with six other learning algorithms on classification tasks, Proceedings of the 4th International Workshop on Learning Classifier Systems (IWLCS ′01), 2001, 337–341.
Google Scholar
186 Kharbat F., Bull L., and Odeh M., Mining breast cancer data with XCS, Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, 2066–2073, https://doi.org/10.1145/1276958.1277362, EID2-s2.0-34548137365.
Google Scholar
187 Unold O. and Tuszyński K., Mining knowledge from data using anticipatory classifier system, Knowledge-Based Systems. (2008) 21, no. 5, 363–370, https://doi.org/10.1016/j.knosys.2008.02.001.
Google Scholar
188 Blake C. and Merz C., UCI repository of machine learning databases, 1998.
Google Scholar
189 Alayón S., Estévez J. I., Sigut J., Sánchez J. L., and Toledo P., An evolutionary Michigan recurrent fuzzy system for nuclei classification in cytological images using nuclear chromatin distribution, Journal of Biomedical Informatics. (2006) 39, no. 6, 573–588, https://doi.org/10.1016/j.jbi.2006.03.001, EID2-s2.0-33750693053.
Google Scholar
190 Unold O., [email protected], Grammar-based classifier system for recognition of promoter regions, 4431, Proceedings of the 8th International Conference on Adaptive and Natural Computing Algorithms (ICANNGA ′07), 2007, 798–805, Lecture Notes in Computer Science, EID2-s2.0-0001387704.
Google Scholar
191 Kovacs T., Evolving optimal populations with XCS classier systems, M.S. thesis, 1996, School of Computer Science, University of Birmingham, Birmingham, UK.
Google Scholar
192 Kovacs T., What should a classifier system learn?, 2, Proceedings of the Congress on Evolutionary Computation, 2001.
Google Scholar
193 Kovacs T., What should a classifier system learn and how should we measure it?, Soft Computing-A. (2002) 6, no. 3, 171–182.
Google Scholar
194 Butz M. and Pelikan M., Analyzing the evolutionary pressures in XCS, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′01), 2001, 935–942.
Google Scholar
195 Butz M. V., [email protected], Kovacs T., [email protected], Lanzi P. L., and [email protected], Wilson S. W., [email protected], Toward a theory of generalization and learning in XCS, IEEE Transactions on Evolutionary Computation. (2004) 8, no. 1, 28–46, EID2-s2.0-0000874753, https://doi.org/10.1109/TEVC.2003.818194.
Google Scholar
196 Bassett J. and De Jong K., Evolving behaviors for cooperating agents, 1932, Proceedings of the 12th International Symposium on Foundations of Intelligent Systems (ISMIS ′00), 2000, 157–165, Lecture Notes in Computer Science.
Google Scholar
197 Butz M. and Goldberg D., Bounding the population size in XCS to ensure reproductive opportunities, Proceedings of the Conference on Genetic and Evolutionary Computation, 2003, 1844–1856, Lecture Notes in Computer Science.
Google Scholar
198 Butz M., Goldberg D., Lanzi P., and Sastry K., Bounding the population size to ensure niche support in XCS, IlliGAl Report, July 2004, no. 2004033.
Google Scholar
199 Butz M., Goldberg D., and Lanzi P., Bounding learning time in XCS, Proceedings of Genetic and Evolutionary Computation Conference (GECCO ′04), June 2004, Seattle,Wash, USA, 739–750.
Google Scholar
200 Butz M., Rule-based evolutionary online learning systems: learning bounds, classification, and prediction, Ph.D. thesis, 2004.
Google Scholar
201 Bull L., Learning classifier systems: a brief introduction, Applications of Learning Classifier Systems, 2004.
Google Scholar
202 Booker L., Representing attribute-based concepts in a classifier system, Foundations of Genetic Algorithms. (1991) 115–127.
Google Scholar
203 Sen S., A tale of two representations, Proceedings of the 7th International Conference on Industrial and Engineering Applications of Artificial Intelligence and Expert Systems, 1994, Gordon and Breach, 245–254.
Google Scholar
204 Riolo R., The emergence of coupled sequences of classifiers, Proceedings of the 3rd International Conference on Genetic Algorithms and Their Application, 1989, San Francisco, Calif, USA, Morgan Kaufmann, 256–264.
Google Scholar
205 Schuurmans D. and Schaeffer J., Representational Difficulties with Classifier Systems, 1988, Department of Computing Science, University of Alberta, Edmonton, Canada.
Google Scholar
206 Stone C. and [email protected], Bull L., [email protected], For real! XCS with continuous-valued inputs, Evolutionary Computation. (2003) 11, no. 3, 299–336, EID2-s2.0-0008154720.
Google Scholar
207 Dam H., Abbass H., and Lokan C., Be real! XCS with continuous-valued inputs, Proceedings of the Workshops on Genetic and Evolutionary Computation, 2005, New York, NY, USA, ACM, 85–87.
Google Scholar
208 Lanzi P. and Wilson S., Using convex hulls to represent classifier conditions, 2, Proceedings of the 8th Genetic and Evolutionary Computation Conference (GECCO ′06), 2006, New York, NY, USA, ACM Press, 1481–1488, EID2-s2.0-33750251248.
Google Scholar
209 Butz M., Kernel-based, ellipsoidal conditions in the real-valued XCS classifier system, Proceedings of the Conference on Genetic and Evolutionary Computation, 2005, 1835–1842.
Google Scholar
210 Butz M., Lanzi P., and Wilson S., Hyper-ellipsoidal conditions in XCS: rotation, linear approximation, and solution structure, Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, 2006, New York, NY, USA, ACM, 1457–1464.
Google Scholar
211 Booker L., Improving the performance of genetic algorithms in classifier systems, Proceedings of the 1st International Conference on Genetic Algorithms, 1985, Mahwah, NJ, USA, Lawrence Erlbaum Associates, 80–92.
Google Scholar
212 Mellor D., A first order logic classifier system, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′05), 2005, New York, NY, USA, ACM Press, 1819–1826, https://doi.org/10.1145/1068009.1068318, EID2-s2.0-32444448393.
Google Scholar
213 Lanzi P., Extending the representation of classifier conditions—part I: from binary to messy coding, 1, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′99), 1999, 337–344.
Google Scholar
214 Tufts P., Dynamic classifiers: genetic programming and classifier systems, Proceedings of the Genetic Programming, 1995, 114–119.
Google Scholar
215 Ahluwalia M., Bull L., Banzhaf W. et al., A genetic programming-based classifier system, 1, Proceedings of the Genetic and Evolutionary Computation Conference, 1999, 11–18.
Google Scholar
216 Lanzi P. and Perrucci A., Extending the representation of classifier conditions—part II: from messy coding to S-expressions, 1, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′99), 1999, 345–352.
Google Scholar
217 Lanzi P., Mining interesting knowledge from data with the XCS classier system, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′01), 2001, 958–965.
Google Scholar
218 Lanzi P., [email protected], An analysis of generalization in XCS with symbolic conditions, Proceedings of IEEE Congress on Evolutionary Computation (CEC ′07), 2007, 2149–2156, EID2-s2.0-27144549349, https://doi.org/10.1109/CEC.2007.4424738.
Google Scholar
219 Bull L. and Hurst J., A neural learning classifier system with self-adaptive constructivism, 2, Proceedings of the Congress on Evolutionary Computation (CEC ′03), 2003.
Google Scholar
220 O′Hara T. and toby.o′[email protected], Bull L., A memetic accuracy-based neural learning classifier system, 3, Proceedings of IEEE Congress on Evolutionary Computation (CEC ′05), 2005, 2040–2045, EID2-s2.0-0033362601.
Google Scholar
221 Carse B. and Fogarty T., A fuzzy classifier system using the Pittsburgh approach, Proceedings of the International Conference on Evolutionary Computation, the 3rd Conference on Parallel Problem Solving from Nature, October 1994, Jerusalem, Israel.
Google Scholar
222 Butz M., Sastry K., and Goldberg D., Tournament selection in XCS, 1869, Proceedings of the 5th Genetic and Evolutionary Computation Conference (GECCO ′02), 2002.
Google Scholar
223 Butz M. V., [email protected], Goldberg D. E., and [email protected], Tharakunnel K., [email protected], Analysis and improvement of fitness exploitation in XCS: bounding models, tournament selection, and bilateral accuracy, Evolutionary Computation. (2003) 11, no. 3, 239–277, EID2-s2.0-0008154720, https://doi.org/10.1162/106365603322365298.
Google Scholar
224 Kharbat F., Bull L., and Odeh M., Revisiting genetic selection in the XCS learning classifier system, 3, Proceedings of the IEEE Congress on Evolutionary Computation, 2005.
Google Scholar
225 Butz M. V., [email protected], Sastry K., and [email protected], Goldberg D. E., [email protected], Strong, stable, and reliable fitness pressure in XCS due to tournament selection, Genetic Programming and Evolvable Machines. (2005) 6, no. 1, 53–77, EID2-s2.0-0001387704, https://doi.org/10.1007/s10710-005-7619-9.
Google Scholar
226 Widrow B. and Hoff M. E., Adaptive switching circuits, 4, IRE WESCON Convention Record, 1960, 709–717.
Google Scholar
227 Venturini G., Apprentissage adaptatif et apprentissage supervise par algorithme genetique, These de Docteur en Science, 1994, Universite de Paris-Sud, Paris, France.
Google Scholar
228 Butz M., Kovacs T., Lanzi P., and Wilson S., How XCS evolves accurate classifiers, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′01), 2001, 927–934.
Google Scholar
229 Liepins G. and Wang L., Classifier system learning of Boolean concepts, Proceedings of the 4th International Conference on Genetic Algorithms, 1991, San Francisco, Calif, USA, Morgan Kaufmann, 318–323.
Google Scholar
230 Weiss G., The Action oriented Bucket Brigade, 1991, Institut für Informatik.
Google Scholar
231 Weiss G., [email protected], Ah action-oriented perspective of learning in classifier systems, Journal of Experimental and Theoretical Artificial Intelligence. (1996) 8, no. 1, 43–62, EID2-s2.0-0027152857.
Google Scholar
232 Butz M. V., [email protected], Goldberg D. E., and [email protected], Lanzi P. L., [email protected], Gradient descent methods in learning classifier systems: improving XCS performance in multistep problems, IEEE Transactions on Evolutionary Computation. (2005) 9, no. 5, 452–473, EID2-s2.0-27144549349, https://doi.org/10.1109/TEVC.2005.850265.
Google Scholar
233 Lanzi P., Butz M. V., and Goldberg D. E., Empirical analysis of generalization and learning in XCS with gradient descent, Proceedings of of the 9th Genetic and Evolutionary Computation Conference (GECCO ′07), 2007, New York, NY, USA, ACM Press, 1814–1821, https://doi.org/10.1145/1276958.1277321, EID2-s2.0-34548070260.
Google Scholar
234 Drugowitsch J. and Barry A. M., XCS with eligibility traces, Proceedings of the Conference on Genetic and Evolutionary Computation Conference (GECCO ′05), 2005, New York, NY, USA, ACM, 1851–1858, https://doi.org/10.1145/1068009.1068322, EID2-s2.0-32444435131.
Google Scholar
235 Lanzi P., [email protected], Loiacono D., [email protected], Wilson S. W., and [email protected], Goldberg D. E., [email protected], Prediction update algorithms for XCSF: RLS, Kalman filter, and gain adaptation, 2, Proceedings of the 8th Genetic and Evolutionary Computation Conference (GECCO ′06), 2006, ACM Press, 1505–1512, EID2-s2.0-27144549349.
Google Scholar
236 Horn J., Goldberg D., and Deb K., Implicit niching in a learning classifier system: nature′s way, Evolutionary Computation. (1994) 2, no. 1, 37–66.
Google Scholar
237 Horn J., Goldberg D., Koza J., Goldberg D., Fogel D., and Riolo R., Natural niching for cooperative learning in classifier systems, Proceedings of the 1st Annual Conference on Genetic Programming, 1996, MIT Press, 553–564.
Google Scholar
238 Butz M. V., Pelikan M., Llorà X., and Goldberg D. E., Extracted global structure makes local building block processing effective in XCS, Proceedings of the Genetic and Evolutionary Computation Conference (GECCO ′05), 2005, New York, NY, USA, ACM, 655–662, https://doi.org/10.1145/1068009.1068121, EID2-s2.0-32444434798.
Google Scholar
239 Butz M. V., Pelikan M., Llorà X., and Goldberg D. E., Automated global structure extraction for effective local building block processing in XCS, Evolutionary Computation. (2006) 14, no. 3, 345–380, https://doi.org/10.1162/evco.2006.14.3.345, EID2-s2.0-33750578932.
Google Scholar
240 Bacardit J. and Krasnogor N., Smart crossover operator with multiple parents for a pittsburgh learning classifier system, 2, Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation (GECCO ′06), 2006, New York, NY, USA, ACM Press, 1441–1448, EID2-s2.0-33750272767.
Google Scholar
241 Serendynski F., Cichosz P., and Klebus G., Learning classifier systems in multi-agent environments, Proceedings of the 1st International Conference on Genetic Algorithms in Engineering Systems: Innovations and Applications (GAESIA ′95), 1995, 287–292.
Google Scholar
242 Sen S. and Sekaran M., Multiagent coordination with learning classifier systems, Proceedings of the Adaption and Learning in Multi-Agent Systems, 1996, 218–233, Lecture Notes in Computer Science.
Google Scholar
243 Bull L., Studley M., Bagnall T., and Whittley I., On the use of rule-sharing in learning classifier system ensembles, 1, Proceedings of the Congress on Evolutionary Computation (CEC ′05), 2005.
Google Scholar
244 Bull L., [email protected], Studley M., [email protected], Bagnall A., and [email protected], Whittley I., [email protected], Learning classifier system ensembles with rule-sharing, IEEE Transactions on Evolutionary Computation. (2007) 11, no. 4, 496–502, EID2-s2.0-0013667772, https://doi.org/10.1109/TEVC.2006.885163.
Google Scholar
245 Bacardit J. and Krasnogor N., Empirical evaluation of ensemble techniques for a Pittsburgh learning classifier system, 4998, Proceedings of the 9th International Workshop on Learning Classifier Systems (IWLCS ′08), 2008, 255–268, https://doi.org/10.1007/978-3-540-88138-4-15, EID2-s2.0-57049107400.
Google Scholar
246 Dam H. H., Rojanavasu P., Abbass H. A., and Lokan C., Distributed learning classifier systems, Studies in Computational Intelligence. (2008) 125, 69–91, https://doi.org/10.1007/978-3-540-78979-6_4, EID2-s2.0-46949099180.
Google Scholar
247 Lokan C., Distributed learning classifier systems, Learning Classifier Systems in Data Mining, 2008.
Google Scholar
248 Ranawana R. and Palade V., Multi-classifier systems: review and a roadmap for developers, International Journal of Hybrid Intelligent Systems. (2006) 3, no. 1, 35–61.
Google Scholar
249 Bernado-Mansilla E., Llorà X., and Traus I., Multiobjective learning classifier systems: an overview, 2005, University of Illinois at Urbana Champaign, Urbana, Ill, USA.
Google Scholar
250 Fu C. and Davis L., A modified classifier system compaction algorithm, Proceedings of the Conference on Genetic and Evolutionary Computation Conference (GECCO ′02), 2002, 920–925.
Google Scholar
251 Butz M. V., [email protected], Lanzi P. L., and [email protected], Wilson S. W., [email protected], Function approximation with XCS: hyperellipsoidal conditions, recursive least squares, and compaction, IEEE Transactions on Evolutionary Computation. (2008) 12, no. 3, 355–376, EID2-s2.0-0001570452, https://doi.org/10.1109/TEVC.2007.903551.
Google Scholar
252 Holmes J., Sager J., and Bilker W., A comparison of three methods for covering missing data in XCS, Proceedings of the 7th International Workshop on Learning Classifier Systems (IWLCS ′04), June 2004, Seattle, Wash, USA.
Google Scholar
253 Orriols-Puig A. and [email protected], Bernadó-Mansilla E., [email protected], Bounding XCS′s parameters for unbalanced datasets, 2, Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation Conference (GECCO ′06), 2006, New York, NY, USA, ACM, 1561–1568, EID2-s2.0-0001387704.
Google Scholar
254 Dam H., Shafi K., and Abbass H., Can evolutionary computation handle large dataset?, no. TR-ALAR-2005070001, 2005, http://seal.itee.adfa.edu.au/~alar/techreps.
Google Scholar
255 Booker L., Classier systems, endogenous fitness, and delayed rewards: a preliminary investigation, Proceedings of the International Workshop on Learning Classifier Systems (IWLCS ′00) in the Joint Workshops of SAB, 2000.
Google Scholar
256 Hurst J. and Bull L., A self-adaptive classifier system, Proceedings of the 3rd International Workshop on Advances in Learning Classifier Systems, 2000, Springer, New York, NY, USA, 70–79.
Google Scholar
257 Bull L. and Hurst J., Self-adaptive mutation in ZCS controllers, Proceedings of the Real-World Applications of Evolutionary Computing, EvoWorkshops, 2000, 339–346, Lecture Notes in Computer Science.
Google Scholar
258 Bull L., Hurst J., and Tomlinson A., Self-adaptive mutation in classifier system controllers, From Animals to Animats 6: Proceedings of the 6th International Conference on Simulation of Adaptive Behavior, 2000, MIT Press.
Google Scholar
259 Hurst J. and Bull L., A self-adaptive XCS, Proceedings of the 4th International Workshop on Advances in Learning Classifier Systems, 2002, 57–73, Lecture Notes in Computer Science.
Google Scholar
260 Browne W., Improving Evolutionary Computation Based Data-Mining for the Process Industry: The Importance of Abstraction, Learning Classifier Systems in Data Mining, 2008.
Google Scholar
261 Goldberg D., Horn J., and Deb K., What makes a problem hard for a classifier system?, 1992, Santa Fe Working Paper.
Google Scholar
262 Booker L. B., Goldberg D. E., and Holland J., Classifier systems and genetic algorithms, Machine Learning: Paradigms and Methods, 1989, 235–282.
Google Scholar
263 Holland J., Booker L., Colombetti M. et al., What is a learning classifier system?, Learning Classifier Systems, from Foundations to Applications, 2000, 3–32, Lecture Notes in Computer Science.
Google Scholar
264 Wilson S. W., State of XCS classifier system research, Proceedings of the 3rd International Workshop on Advances in Learning Classifier Systems, 2000, 63–82, Lecture Notes in Computer Science.
Google Scholar
265 Kovacs T., Learning classifier systems resources, Soft Computing-A. (2002) 6, no. 3, 240–243.
Google Scholar
266 Drugowitsch J., Design and Analysis of Learning Classifier Systems: A Probabilistic Approach, 2008, Springer, Berlin, Germany.
Google Scholar

Citing Literature

All articles

Learning Classifier Systems: A Complete Introduction, Review, and Roadmap

Abstract

1. Introduction

2. A General LCS