Optimizing the Operation Sequence of a Multihead Surface Mounting Machine Using a Discrete Particle Swarm Optimization Algorithm
Abstract
The optimization of the nozzle selection, for sequencing component pick and place operations, is very important to the efficiency of multihead surface mounting machine (SMM). The nozzle change operation, that is, choosing the best nozzle head relative pair that is most effective for picking and placing components onto the printed circuit board (PCB), significantly adds to the overall assembly time. In this paper, as a practical application, we focus on a discrete particle swarm optimization (DPSO) algorithm for multihead SMM which is used to minimize the number of nozzle change operations and pick and place operations simultaneously. To evaluate the performance of the proposed algorithm, we test it on assembly tasks of PCBs through simulations. The results of computer experiments show that this DPSO algorithm was superior to the standard PSO algorithm.
1. Introduction
The optimization of feeder setup and component placement sequences is very important to the efficiency of a surface mount machine (SMM). The increase of the number of components to be placed on a single board has made the reduction of assembly time probably the most important issue to further cut down production costs and increase productivity. The assembly of printed circuit board (PCB) on a production line can be divided into four process-planning subproblems: grouping (i.e., assigning PCB types to product families and to machines), allocation (i.e., assigning nozzles to the heads), arrangement (i.e., assigning reels to slots on the feeder rack), and sequencing (i.e., the components′ pick-and-place operations). Many publications have been devoted to these complex optimization subproblems, and various models and techniques have been presented, for example, by Ball and Magazine [1] and Brad et al. [2]. These subproblems are tightly intertwined, and each of them is very difficult to solve to optimality. For example, the quality of a component pick-and-place sequence is dependent on the feeder setup and vice versa [2]. Various approaches have been proposed to improve sequence of placement points and/or feeder assignment for the PCB assembly process [3]. Egbelu et al. [4] investigated assigning components to feeder slots and sequencing component placement onto the PCB in order to minimize the total assembly cycle time. They classified machines depending upon whether the PCB table and the feeder carrier were stationary or not. They developed rules such as the centroid rule, the proportion rule, the partition rule, and the weighted rule to initially assign components to feeder slots. To obtain the component insertion sequence, they modeled the problem as a traveling salesman problem (TSP). Finally, by having the component insertion sequence and the initial feeder setup, Egbelu et al. [4] converted the component slot assignment into a quadratic assignment problem (QAP) where the cutting plane and exchange heuristic were used. Results showed that the assembly cycle times were minimized when both the feeder rack and PCB table were able to move (Egbelu et al. [4]). Some researchers (see, e.g., [5]) have tackled the subproblems independently but also have some researchers (see, e.g., Ho and Ji [6] ) preferred to solve these subproblems in an integrated way. The literature is rich with work that has tackled this subject, especially investigating how to improve the efficiency of SMM [7, 8]. The technological characteristics of the SMM can also influence the nature of some of the subproblems to be solved and the formulation of the associated models [9]. As a result, many researchers solved the problem as a unique problem since the problem relies heavily on the machine characteristics (Ho and Ji, 2003). This causes difficulties in applying or comparing the various approaches from the literature.
In the recent years, a heuristic approach was developed to solve the subproblems. Genetic algorithms (GAs) have been applied successfully to a wide variety of optimization arrangement/sequencing problems [10]. The GA and its many versions have been popular in academia and the industry mainly because of their intuitiveness, ease of implementation, and the ability to effectively solve highly nonlinear, mixed integer optimization problems that are typical of complex engineering systems. The drawback of the GA is its expensive computational cost. Particle swarm optimization (PSO), introduced by [11] is a relatively recent heuristic search method whose mechanics are inspired by the swarming or collaborative behavior of biological populations. PSO is similar to the GA in the sense that these two heuristics are population-based search methods. In other words, PSO and the GA move from a set of points (population) to another set of points in a single iteration with likely improvement using a combination of deterministic and probabilistic rules. Critical ingredients for the success of PSO are simplicity, ease of operation, and great flexibility.
When the SMM has more than one nozzle per head (or even a single nozzle per head), choosing an effective nozzle group (or a nozzle) is important since a nozzle change operation is time consuming. Optimizing the pick and place operations without considering the nozzles changing operations may not be efficient since it may cause many unnecessary nozzle changes that will significantly reduce the machine throughput. However, to date, only a few researchers [3] have tackled the nozzle optimization problem. Due to its global and local exploration abilities, simplicity in coding and consistency in performance, PSO has been widely applied in many fields beyond its original applications to the solution of continuous optimization problems. In our research, we mainly use discrete data to process SMM problems. Therefore, developing a mechanism to realize discrete optimization problem is attractive. Hence, in this paper, we develop a discrete particle swarm optimization (DPSO) algorithm for nozzles selection and sequencing components pick and place operations in a SMM equipped with multiple placement heads. The objective of the algorithm is to minimize the nozzle selection for sequencing component pick and place operations so as to increase the machines throughput.
The organization of this paper is as follows. Section 2 is a description of the SMM problem and its assumptions. In Section 3, we propose a DPSO algorithm for multihead SMM which is used to minimizing the nozzle changes and minimizing the pick and place operations. The fourth section discusses the experiment results we have gained for the heuristics described in this paper applied to 10 test print circuit boards of SMM. The last section covers the conclusions we have drawn from this research and gives a brief overview of planned future research.
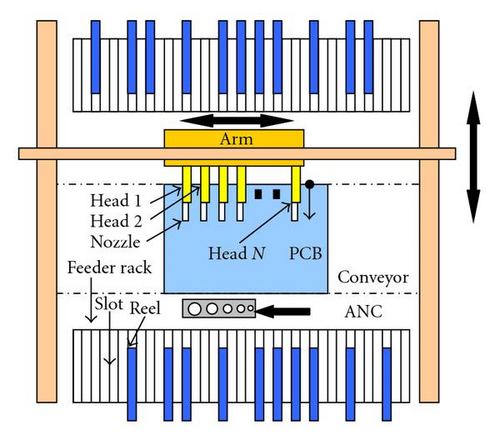
2. SMM Description and Assumptions
- (1)
The number of heads is not limited. That is the arm may have any number of heads.
- (2)
The different types of components cannot be contained in one reel.
- (3)
The number of reels required to complete the job is, at most, equal to the capacity of the feeder racks.
3. Discrete Particle Swarm Optimization Algorithms
PSO is inherently continuous but recently the discrete particle swarm optimization algorithm has been proposed to solve discrete problems successfully. Ucar and Tasgetiren [12] proposed a discrete particle swarm optimization algorithm to determine a sequence of n jobs to be processed through m machines that minimizes the number of tardy jobs. Other papers proposing discrete particle swarm optimization algorithms can be found in Shen et al. [13], Tasgetiren et al. [14], Onwubolu [15], and Clerc [16].
Since, for each printed circuit board, the location of each component has been decided, the critical decisions left for optimization are where the different reel groups should be placed in feeder slots. Moreover, in the multihead case, the optimal solution does not only require the local optimization of a single head but also the global optimization of the head group. In addition, there is only a finite number of feeder slots, and each feeder slot can only contain one reel of component(s). These properties match the properties of particle swarm optimization that is why we propose the DPSO algorithms to solve the SMM′s arrangement/sequencing problems.
Considering the characteristics of the multihead case, we decompose the component arrangement/sequencing problem into three phases: assignment of reels to heads, construction of reel-groups, and the assignment of component placement. In phase I, heads assignment algorithm, the most critical decision is to assign jobs to each head with a balanced loading simultaneously. Therefore, in order to balance the loading of each head, first, we construct a head-nozzle relative matrix; then, an algorithm is developed to minimize the variance of component loadings on each head based on the component types and their associated nozzle types to produce an optimal solution of head assignment.
3.1. Phase I: Heads Assignment Algorithm
In order to balance the loading of each head, the heads assignment algorithm essentially solves the following linear programming problems. Let H be the head set where Hi denoted the nozzle types which assigned to head i. Let N be the nozzle set where Nj is the set which contained the components associated with the nozzle type j, and let Mj be the number of components associated to nozzle type j. Then,
Step 1.1. Construct a head-nozzle relative matrix A(i, j) through randomly assigning each nozzle to each head and satisfied:
Step 2.2. Calculate the fitness of head assignment to minimize the variance of component loading on each head:
3.2. Phase II: Reel Grouping Optimization
In phase II, since the time for the operation of pick-and-place for each component is constant, the only difference is how many nozzle changes are needed in the pick-and-place process. The assignment of nozzles to each head was optimally determined by phase I; therefore, the next objective is to minimize the total number of times of nozzle changes in the pick-and-place process according to the different type of nozzle needed. In addition, each reel on the feeder rack can only hold one kind of component. The optimal number of reel groups needed to minimize the number of times of nozzle changes can be developed as follows.
Step 1.1. Based on phase I, construct a matrix of component assigned for the head group, that is H = AN ≈ Hi = ∪A(i, j) × Nj.
Step 2.2. From the component matrix, randomly assign components to each head and generate the reel group, {reel_groupi(j, k) | 1 ≤ i ≤ No_reel_group}, where reel_groupi(j, k) means that the component assigned to head k on the jth row for the ith reel group.
Step 3.3. Determine whether it is necessary to change the nozzle from the consecutive component group assignment, if so, calculate the number of nozzle changes and create a new reel group, otherwise, continue the assignment process.
3.3. Phase III: DPSO for Assignment of Component Placement
In Phase III, the assignment of component placement based on particle swarm optimization approach is developed in order to minimize the total time of pick-and-place calculated by the traveling distances, one dimension Euclidean distance times the unit assembly time in the entire process. The discrete particle swarm optimization (DPSO) approach is used to search the optimal locations for the reel group. Since the number of feeder slots in each surface mounting machine is finite and discrete, each particle cannot fly outside the range of feeder rack, that is, the position of each particle is constrained. In order to satisfy these constrains, the V max velocity update equation is used in this case, and the maximum velocity which each particle can fly is calculated as the half of the number of feeder slots. Furthermore, Zhang et al. [17] proposed a new boundary handling method, which is called as “periodic mode.” It provides an infinite search space for the flying of particles, which is composed of periodic copies of original search space with same fitness landscape. Since each feeder slot can only contain one reel, some modification on the position update equation with boundary constraints handling should be made to protect against infeasibility.
The algorithm for component placement is given below.
Step 1.1. An individual particle of reel groups is randomly assigned to a feeder rack, and an initial solution based on the optimal assignment of reel groups from Algorithm II is generated according to the fitness function:
Step 2.2. Run the iterations of population with the following update equation.
- (i)
Update the velocity with maximum velocity, V max , constrained within the range of feeder rack. The velocity update equation is influenced simultaneously by the individual′s experience and neighbor′s experience as follows:
()where w is the inertia weight in the range [0, 1], the cognitive parameter c1 ∈ [0.5, 2], and the social parameter c2 ∈ [1, 3]. - (ii)
Update the particle′s position using the new velocity:
() - (iii)
If the reel allocation is out of boundary, then a boundary constraint handling modification on position updating is made as the follows:
()If the reel allocation is infeasible, then go to (i) again.
Step 3.3. Based on the fitness function, update Pid and Pgd.
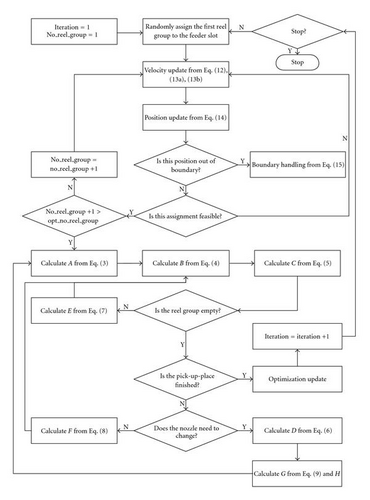
Figure 2 shows the flowchart of the DPSO for optimization of the operation sequence placement in multiheaded SMM.
4. Experiment Results
According to the DPSO approach proposed in Section 3, even though we only considered one machine to one printed circuit board, there are many possibilities of combination of processing procedures. Depending on what nozzle is assigned to what head or what component is assigned to what reel of each head different solutions will emerge. In this section, we consider a practical SMM that has 3 heads for a 300 × 250 mm2 board. In order to emphasize the effectiveness of DPSO, we made a comparison of the standard PSO approach with our DPSO approach according to the quality of solution found. This is measured by the optimal solution found, the average traveling time (unit assembly time), the improvement percentage, and paired t-test for significance. The computer simulation is performed in the operating environment of Window XP Professional with Pentium III CPU, 846 MHz, 1 GB RAM. The software was coded in MATLAB 7.0.
Since the exhaustive examination of the quality of solutions requires a large number of problems, the algorithm is tested on a set of randomly generated problems. The component locations on the print board are randomly determined. In these simulations, both DPSO and the standard PSO use the same parameters. Namely, the population size is 10, and the relative parameters of velocity update equation, the cognition parameter c1, and the social parameter c2 are set equal to 2 to result in the most effective search of the problem domain [11]. Furthermore, a linear decreasing inertia weight w is used in this simulation.
To illustrate the performance of this meta-heuristic approach, the number of placements and component types ranged between 21 and 210 components to be placed and of up to 34 different component types. Tables 1 and 2 show the results of 10 different PCB boards with 20 runs with a different random seed for each problem case.
| Average time | Opt_solution_time | Improvement | Paired t test | ||||
|---|---|---|---|---|---|---|---|
| Components | DPSO | PSO | DPSO | PSO | DPSO | PSO | α = 0.05 |
| 21 | 372 | 375 | 311 | 335 | 16.3% | 10.63% | 0.2893 |
| 42 | 1345 | 1351 | 1166 | 1172 | 13.3% | 13.25% | 0.4187 |
| 63 | 1686 | 2243 | 1477 | 1990 | 12.38% | 11.29% | 0.0000* |
| 84 | 3916 | 4732 | 3411 | 4203 | 12.90% | 11.17% | 0.0000* |
| 105 | 5925 | 6033 | 5282 | 5389 | 10.86% | 10.67% | 0.3853 |
| 126 | 5986 | 7277 | 5357 | 6607 | 10.50% | 9.21% | 0.0000* |
| 147 | 7038 | 8562 | 6287 | 7937 | 10.67% | 7.30% | 0.0000* |
| 168 | 8087 | 9684 | 7443 | 8845 | 7.96% | 8.67% | 0.0000* |
| 189 | 9091 | 11013 | 8667 | 10417 | 4.67% | 5.41% | 0.0000* |
| 210 | 11793 | 12379 | 10005 | 11617 | 15.16% | 6.15% | 0.0122* |
- *means that the paired t-test is significant, that is, p < α/2.
| Components | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 21 | 42 | 63 | 84 | 105 | 126 | 147 | 168 | 189 | 210 | |
| Approaches | ||||||||||
| DPSO | 16.5 | 32 | 51 | 77 | 94 | 117 | 137 | 163 | 190 | 204 |
| PSO | 16.65 | 33 | 52 | 82 | 106 | 120 | 152 | 173 | 196 | 216 |
| Saving (%) | 0.91 | 3.03 | 1.92 | 6.10 | 11.32 | 2.50 | 9.87 | 5.78 | 3.06 | 5.56 |
- *Saving = (CPU time of PSO-CPU time of DPSO)/ CPU time of PSO *100%.
From Table 1, it is easy to see that the DPSO outperforms the standard PSO in every case; particularly, as the number of components increased, the difference in performance is more significant. Moreover, with the reversed modification of boundary handling in (15), the CPU time needed to search the optimal solution through DPSO is a little shorter than the time taken by the standard PSO, as shown in Table 2.
It shows that DPSO outperforms the standard PSO on the ability to find the optimal solutions, and the performance improvement is shown in Table 2. From the significance t-paired test, we also can see that the performance of DPSO is better than the performance of standard PSO in PCB component assignment/sequencing problems.
5. Conclusion
In this paper, we proposed a DPSO approach to solve the problem of minimizing the PCB assembly time and simultaneously optimizing assignment/sequencing problems for multiheaded SMM. We decomposed the DPSO approach into three phases: heads assignment algorithm, reel grouping optimization, and the assignment of component placement. These results lead to minimize the total assembly time of assignment/sequencing time of the placement of component on PCB board. From the experiment results, the DPSO outperforms the standard PSO in the quality of the solution found and in the time taken to search for the optimal solution.
In this paper, we only discuss the application of DPSO in a SMM. But, it is easy to modify the DPSO approach for different applications including the consideration of component placement for multiple printed circuit boards operation simultaneously and with time limitation on operations. In addition, the different parameter selection for the DPSO and different velocity updating equation selection applied in DPSO can be compared and considered.
Nomenclature
-
- :
-
the individual particle previous velocity.
-
- :
-
the updating velocity of individual particle in next movement.
-
- V max :
-
the limitation velocity updating is calculated by half of the number of slots.
-
- Nij:
-
the nozzle of type j assigned to head i in the head-nozzle relative matrix.
-
- :
-
the previous position of individual particle.
-
- :
-
the updating position of individual particle.
-
- :
-
the position of nozzle.
-
- :
-
the position of reel group.
-
- Xid:
-
the current position of individual particle.
-
- Pid:
-
the best-so-far position of individual particle.
-
- Pgd:
-
the best-so-far position of neighbors.
-
- no_change:
-
the number of nozzle changes in need.
-
- no_component:
-
the number of components used in board.
-
- Average_loading:
-
the average of component loading at each head is calculated by dividing the number of components by the number of heads.
Acknowledgment
The authors would like to thank the reviewers for their valuable suggestions and advices to improve the quality of the paper.
Appendix




