A Strongly Interacting Dynamic Particle Swarm Optimization Method

2.1. Computation of Particle Trajectories

In practice, these equations are solved numerically by discretizing the time interval into time steps δ, and computing for i = 1, 2, …, np approximations x^k{i} to x{i}(t_k) and v^k{i} to v{i}(t_k) at discrete time mesh points t_k = kδ, k = 0, 1, 2, …, by some suitable numerical integration scheme. Here, we use the simple leap-frog numerical integration scheme of Greenspan [4].

This scheme has been found to be stable for sufficiently small time steps δ. It is also approximately energy conserving in the absence of energy dissipating forces, and was successfully used in the original single-particle dynamic method of Snyman [1].

2.2. The Interacting Force Law

In the original dynamic method of Snyman [1, 2], a single particle is considered. The force a acting on this particle is equal to the negative of the function gradient. Since we propose a direct search method, we no longer have gradient information available. Rather, we will use information available in the swarm to generate the particle forces.

This proposed force law is in contrast to the standard PSO, where particles are attracted to historic positions (personal and global bests) rather than the current position of other particles. In addition, this force law automatically results in a dynamic neighborhood, where it is possible that completely different particles exert forces on particle i in iteration k + 1, as compared to iteration k. In a given iteration k, the complete range of interaction is also covered. One extreme is the particle with the current worst function value, which experiences forces from all other particles. The other extreme is the particle with the current best function value, which experiences no force and travels at constant velocity.

2.3. Energy Dissipation Strategy

In computing the trajectories of the particles x^k{i}, i = 1, 2, …, np, for k = 0, 1, 2, …, the function values f_k(i) = f(x^k{i}) at x^k{i} are monitored at each iteration k so that the best (lowest) function value f_b{i} and the corresponding best position x^b{i} along each trajectory i are recorded. The current overall globally best function value f_g = min⁡_i(f_b{i}) and the corresponding position x^g are also recorded.

The following energy dissipation strategy is now applied to ensure local descent of a particle and the overall collapse of the swarm to a local minimum. Whenever a particle i moves “uphill” at iteration k, that is, when f_k+1{i} > f_k{i}, then set x^k+1{i}: = [2x^k{i} + x^b{i} + x^k+1{i}]/4 and set v^k+1{i}: = [v^k+1{i} + v^k{i}]/4. Notice that the current velocity v^k+1{i} is recomputed to be half the average velocity over the past two time steps. This interference will normally result in a decrease in kinetic energy and together with the “backward” adjustment of the position x^k+1{i} will initiate controlled motion of the particle towards a position of lower function value. The trajectory of particle i is assumed to have converged if the relative function value difference from iteration k to k + 1, that is, |f_k+1{i} − f_k{i}|/(1+|f_k+1{i}|), is less than some prescribed tolerance ε. The computation of the trajectories are continued until a sufficient number (npc) of the particles have converged to a stationary point. In practice, we choose npc = min⁡[n,np].

A formal presentation of the basic DYN-PSO algorithm is presented in Algorithm 1. For the sake of clarity and simplicity of presentation of the algorithm, the function value computation and monitoring procedure, and the recording of best local f_b{i} and global f_g function values and corresponding best local and global positions, x^b{i} and x^g are not explicitly listed, but are implicitly assumed to be done in the execution of Algorithm 1. Also the computation of the forces a^k{i}, i = 1, 2, …, np, according to (4), is assumed to have been done as the need for the a^k{i} arises in Algorithm 1.

2.4. Selection of Suitable Integration Time Step

An outstanding matter is the selection of an appropriate time step δ to be used in the leap-frog integration scheme. This value can be chosen arbitrarily, but if chosen too large may result in individually erratic and unstable trajectories that fail to converge because of very large zigzagging steps being taken in space. On the other hand, if δ is too small, the steps in space will be correspondingly small and the collapse of the swarm may be very slow, requiring an excessively large number of iterations for convergence.

Many different schemes may be proposed to automatically select and control the time step so that acceptable convergence rates are obtained. Here, we firstly select an initial time step which guarantees sufficiently large trajectory steps in space for all the particles. Secondly, after the trajectories are initiated, for each iteration k and for each particle i, the magnitude of the actual step taken in space is monitored; and if larger than some specified step limit, the time step associated with the particular trajectory is reduced, that is, we now allow for different time steps δ{i}, i = 1, 2, …, np, for the different particles. The details of these additional automatic time step control procedures follow below.

In Step 1 of Algorithm 1, after the generation of the np random particles, compute the average magnitude $$ of the forces acting on the particles $$. An associated average computed initial step size follows from the leap-frog scheme as $$. Requiring initially, on average, a step size of Δx = D, where D is the diameter of the initial variable “box", we initially select as sufficiently large initial time steps $$, which is now inserted in Step 1 just after the generation of the initial random particle positions. However, for a particular particle, this initial choice for the time step may still be too large and result in erratic behavior along the computed trajectory. Thus, as a further control measure, the magnitude of the step taken by each particle is monitored at each iteration, and if it exceeds a specified limit x_lim, the current velocity is scaled down by a factor x_lim/∥x^k+1{i} − x^k{i}∥, the particle′s time step for subsequent steps is reduced by a factor α, and the step to x^k+1{i} is recomputed using the rescaled velocity and new time step. More specifically, we introduce at the end of Step 2 of Algorithm 1, for each iteration k and for each particle i, the additional procedure given in Algorithm 2.

In practice, good choices for the additional parameters introduced here are x_lim = D/2 and α = 0.5. These values are used in the numerical tests that are reported here.

One complication of the above strategy arises if the nature of the cost function changes dramatically as the search proceeds. The initial time steps are appropriate during the initial stages of the search. However, the average force acting on the particles often decreases over time. Hence, the average particle step size also decreases over time. This seems appropriate for swarm convergence, but the step size decrease may be excessive if the average magnitudes of the forces computed by (4) decrease dramatically. This typically happens in the neighborhood of a local minimum of highly nonlinear functions. To overcome this drawback, we simply recompute the time steps $$, whenever appropriate, using the recomputed average force $$. For all the results presented in this paper, the time steps are recomputed every 100 iterations.

3.1. Illustrative Two-Dimensional Trajectories

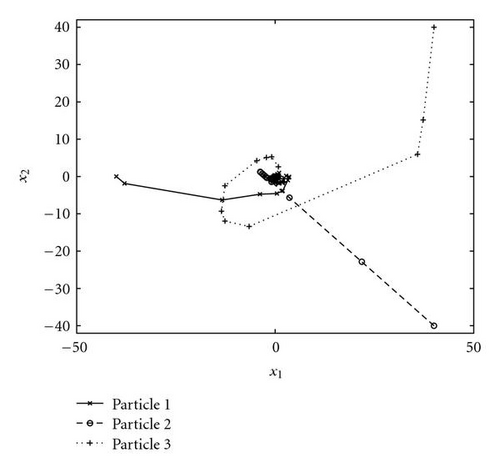
To illustrate the mechanics of the DYN-PSO algorithm, we compute the trajectories for $$ with 3 particles, that is, the case n = 2 with np = 3. As starting points, we select the vertices (40, 40);  (−40, 0);  (40, −40). Figure 1 depicts the three computed trajectories (using diameter D = 100) up to the 30th iteration at which point f_g = 9.48 × 10⁻⁴, with $$.

3.2. Choice of Number of Particles

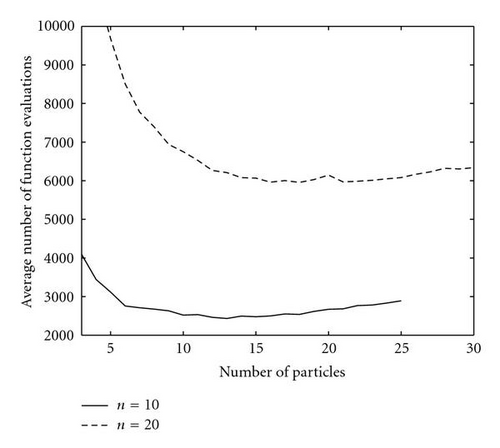
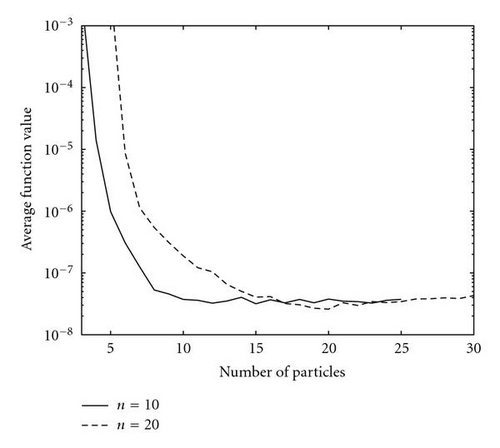
Throughout the numerical experiments done here, the number of particle trajectories required to converge before termination of the algorithm is taken as npc = min⁡[n,np]. It is now required to obtain an indication of what is a good or an optimum choice for the number of particles np to be used for “normal" problems where one expects a single unique global minimum in the region of interest. To get an indication of what it should be, some experiments were performed (with function value tolerance ε=10⁻⁸) on the extended homogeneous quadratic test function (see list of test problems) for n = 10 and n = 20, using different values for np and determining the average number of functions evaluations (over 100 independent runs) required for successful convergence in each case. The variation of the number of function evaluations against np is shown in Figure 2. Note that for n = 20, the number of function evaluations appears to be almost insensitive to np over the range np = 15 to np = 25, with a variation of less than 4 percent being recorded. The corresponding variation of average function value at convergence with np is depicted in Figure 3. The results appear to indicate that in general a choice of np = n + 1 (i.e., with the positions of the particles defining the vertices of an n-dimensional simplex in Rⁿ) is probably a good one. Consequently, the choice np = n + 1 is used throughout the experiments performed in the next subsection. Since this guideline is based on a very narrow test, some future effort should be directed towards improved guidelines to determine the number of particles. It is anticipated that highly multimodal problems might benefit from an increased number of particles.

3.3. Performance on a Set of Test Functions

The newly proposed DYN-PSO algorithm is tested on the following eight test problems.

Two common scenarios exist to terminate optimization algorithms. First, some convergence criteria are satisfied, which indicates that no substantial improvement is likely and search can terminate. Alternatively, a maximum number of function evaluations may be specified. For the test problems considered here, both these scenarios occur. The many local minima present in the multimodal Griewank and Rastrigin test functions prevent the majority of particle trajectories to converge, hence these problems are terminated based on a maximum allowable number of function evaluations. The proposed convergence criteria work well for all the remaining test functions, where we used a convergence tolerance of ε=10⁻⁸.

The STD-DYN and DYN-PSO algorithms always locate the global minimum for the homogeneous quadratic, Oren′s power function, Neumaier 3, Manevich and Zakharov problems. The STD PSO fails to do so for the 30D Neumaier problem. Also note that out of these 5 test problems, the STD-DYN algorithm is most efficient on the homogeneous quadratic, Oren′s power function, and the Zakharov function, all of which are unimodal. The DYN-PSO algorithm performs best on the Neumaier 3 problem and the 30D Manevich function. STD PSO is only more efficient than the DYN-PSO algorithm for Oren′s power function.

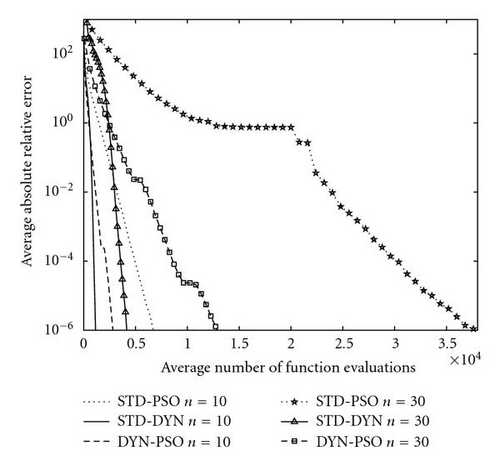
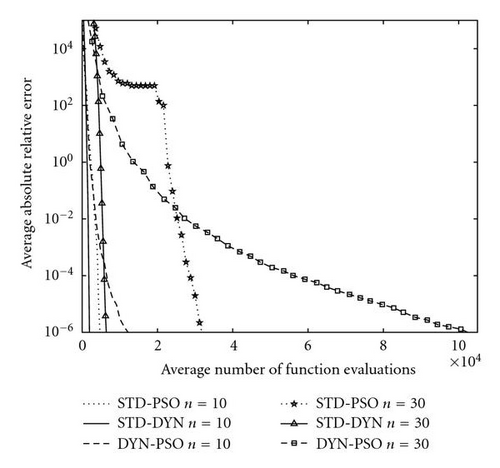
In the case of the Rosenbrock test function, the DYN-PSO algorithm does not always locate the global minimum. In those cases in which the global minimum is not found, the algorithm converges to the only other local minimum, as reported by Shang and Qiu [13]. In the Rosenbrock experiments, 89 and 96 of the 100 runs converged to the global minimum, for n = 10 and 30, respectively. The STD-DYN method locates the global minimum 83 and 88 times, for n = 10 and 30, respectively. Note however that the number of function evaluations is more than a factor 10 less compared to the DYN-PSO algorithm. In the case of the STD-PSO algorithm, the majority of runs do not converge to either the global or local minimum. The number of runs that has a global best less than 1 after 3 × 10⁵ function evaluations is 98 and 4, respectively, for n=10 and 30. The absolute relative error in Figure 6 is computed by only averaging over those runs that converge to the global minimum (DYN PSO and STD DYN) or those that have a global best less than unity after 3 × 10⁵ function evaluations (STD PSO).

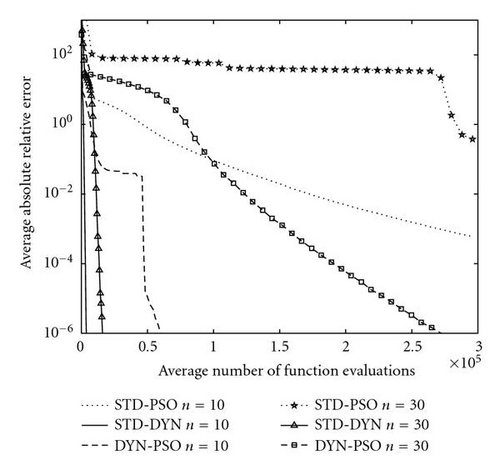
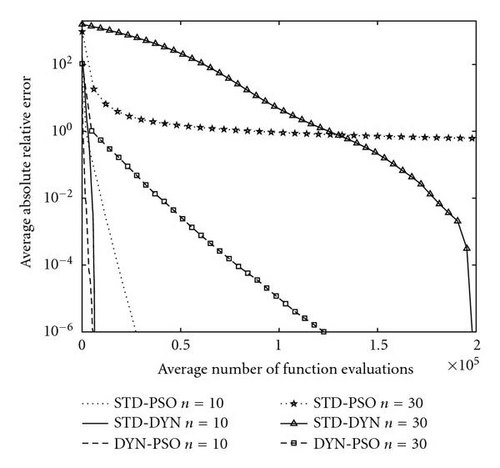
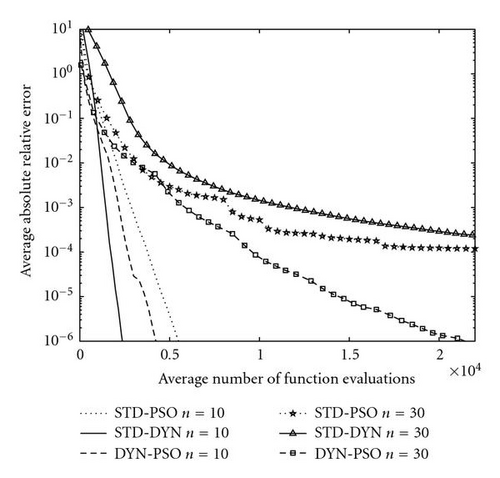
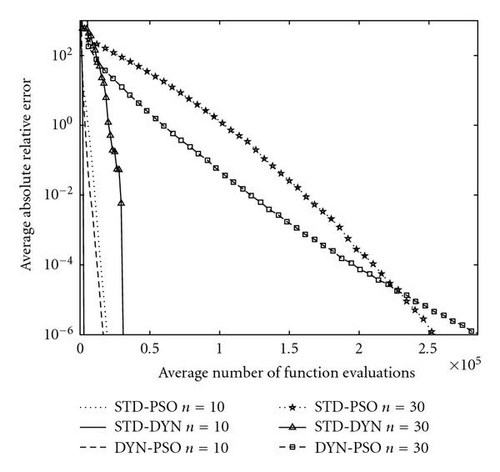
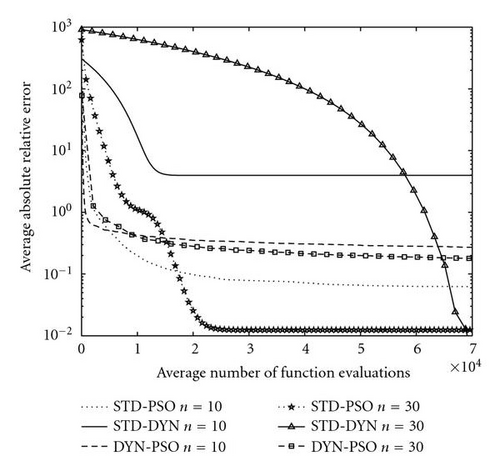
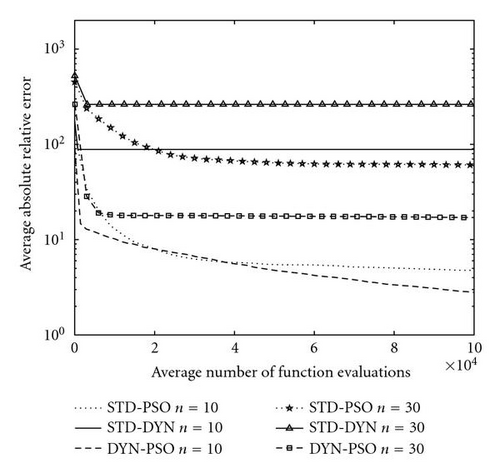
Finally, the DYN-PSO algorithm never locates the global minimum for the multimodal Griewank and Rastrigin test functions. The dynamic method, which is the backbone of the DYN-PSO algorithm, was developed as a local minimizer. However, the energy dissipation strategy we opted in the DYN-PSO algorithm is unchanged from that of the original dynamic method. This strategy is quite severe on “uphill” moves and hence energy is lost quickly if many local minimizers are present, such as in the Griewank and Rastrigin test functions. Nevertheless, compared to the performance of the STD-DYN method, the DYN PSO is vastly superior on the Rastrigin test function. The STD-DYN method simply locates the first strong local minimum and cannot escape it. On the Griewank function, DYN PSO is superior to STD DYN for 10D, and vice versa for 30D. The STD PSO however far outperforms both STD DYN and DYN PSO for the Griewank function. However, in our experience, the performance of the DYN-PSO algorithm is still comparable to that of more traditional global optimization algorithms. The current algorithm does demonstrate the ability to escape some local minima, similar to the standard PSO algorithm. The performance on the 30D Rastrigin function is especially noteworthy, with a mean function value less than 20 after only 5 000 function evaluations. This is obtained with the standard settings proposed here, with no tuning of parameters to suit the problem.

In summary, the DYN-PSO algorithm seems to inherit the desired properties from both its ancestors. It can efficiently solve unimodal functions, sometimes even more efficiently than the gradient-based local minimizer it is based on, for example, the 30D Manevich problem. This is achieved without making use of gradient information. Therefore, the DYN-PSO method might even work for discontinuous problems. This efficient local character is blended with nonlocal behavior, where the swarm provides sufficient information to solve multimodal problems, illustrated best on the Rastrigin function.